leetcode-645：最大二叉树

问题

给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的最大二叉树
定义如下：

• 二叉树的根是数组 nums 中的最大元素
• 左子树是通过数组中最大值左边部分递归构造出的最大二叉树
• 右子树是通过数组中最大值右边部分 递归构造出的最大二叉树

返回有给定数组 nums 构建的 最大二叉树

示例 1：

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1]

    - 空数组，无子节点
    `- [2,1]` 中的最大值是 `2` ，左边部分是 `[]` ，右边部分是 `[1]` 
        - 空数组，无子节点
        - 只有一个元素，所以子节点是一个值为 `1` 的节点
`- [0,5]` 中的最大值是 `5` ，左边部分是 `[0]` ，右边部分是 `[]` 
    - 只有一个元素，所以子节点是一个值为 `0` 的节点
    - 空数组，无子节点

示例 2：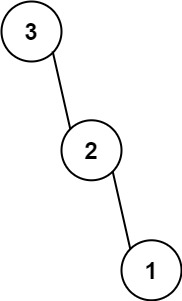

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

解法一：递归

采用前序遍历，因为先构造根节点，然后递归构造左子树和右子树

class Solution {
    // 在左闭右开区间[left, right)，构造二叉树
    TreeNode traversal(int[] nums, int left, int right) {
        if (left >= right){ 
            return null;
        }

        // 分割点下标：maxValueIndex
        int maxValueIndex = left;
        for (int i = left + 1; i < right; ++i) {
            if (nums[i] > nums[maxValueIndex]){
                maxValueIndex = i;
            }
        }

        int idx = nums[maxValueIndex];
        TreeNode root = new TreeNode(idx);

        // 左闭右开：[left, maxValueIndex)
        root.left = traversal(nums, left, maxValueIndex);

        // 左闭右开：[maxValueIndex + 1, right)
        root.right = traversal(nums, maxValueIndex + 1, right);

        return root;
    }

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return traversal(nums, 0, nums.length);
    }
}

• 时间复杂度：。方法 traversal一共被调用 n 次。每次递归寻找根节点时，需要遍历当前索引范围内所有元素找出最大值。一般情况下，每次遍历的复杂度为 ，总复杂度为 。最坏的情况下，数组 nums 有序，总的复杂度为
• 空间复杂度：。递归调用深度为 n