06 | 树：如何深度运用树的遍历？

数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育

数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育

树在我们的应用程序中非常常见，大部分语言的 Map 数据结构，大多是基于树来实现的。此外还经常会遇到很多其他树结构的变种，比如 MySQL 会使用 B+ 树、MongoDB 会使用 B- 树。其中二叉树是各种树的基础，相关的题目也是变化多样，因此，各大公司都喜欢通过二叉树，考察面试者对语言底层数据结构的理解。

二叉树的结点定义较为简单，一般采用如下方式来定义：

public class TreeNode {
int val = 0;
    TreeNode left = null;
    TreeNode right = null;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
}

一个树的结点里面分别存放着：

• 值：用 val 表示
• 左子结点：用 left 指针表示
• 右子结点：用 right 指针表示

在我学习二叉树的过程中，发现很多问题实际上都可以通过二叉树的遍历进行求解。 二叉树的遍历可以分为以下 4 种：

• 前序遍历
• 中序遍历
• 后序遍历
• 层次遍历

在 “第 02 讲” 我们已经介绍了层次遍历，因此，本讲会重点介绍前 3 种遍历以及它们的深度运用。由于二叉树关联的面试题目考察的重点都是在各种遍历上，所以在讲解时，我会采用更加单刀直入的方式，带你开启一段 “爬树” 的旅程。

前序遍历

前序遍历的顺序为：

1. 遍历根结点
2. 左子树
3. 右子树

这里我们不再按照课本上一步一步演示的方式。将采用整体概括处理的方式，比如把左子树或者右子树作为一个整体来处理，如下图所示：

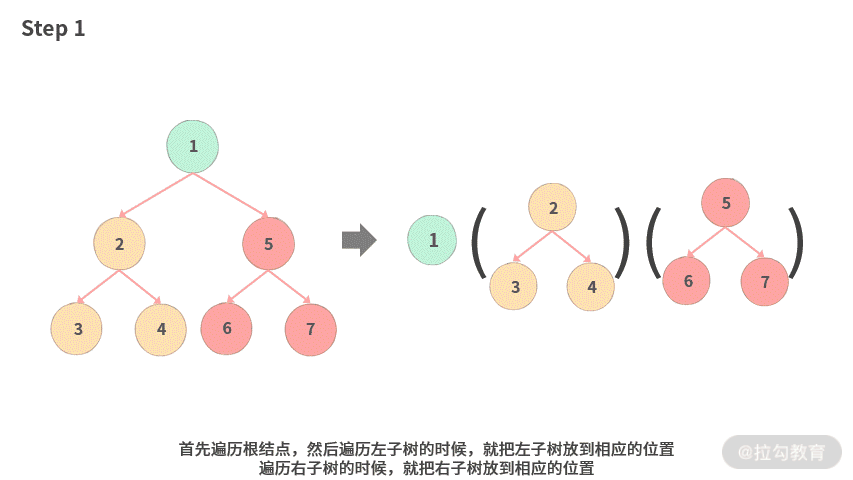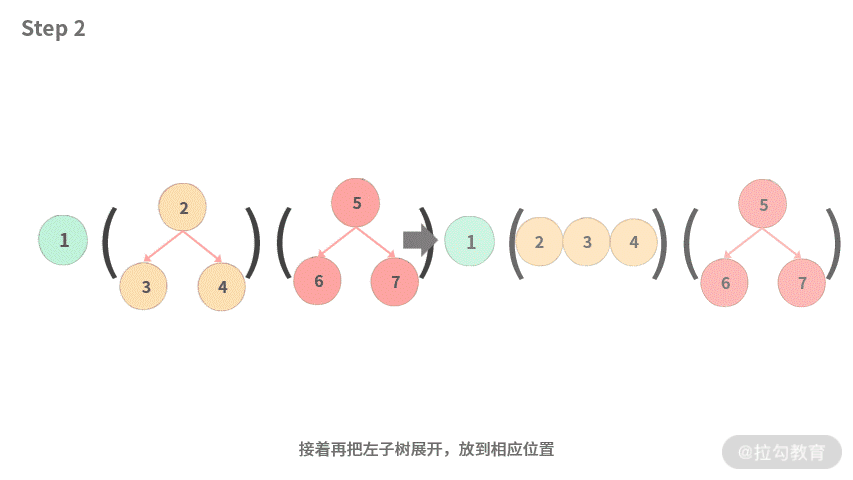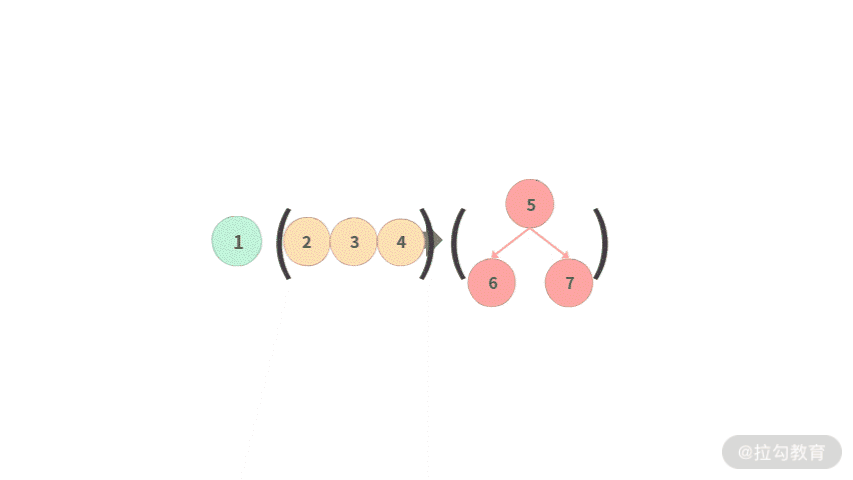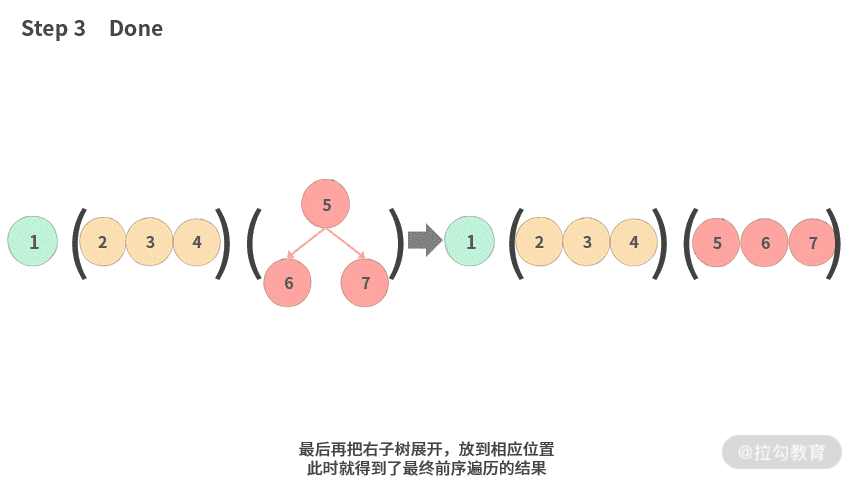
• Step 1. 首先遍历根结点，然后遍历左子树的时候，就把左子树放到相应的位置；遍历右子树的时候，就把右子树放到相应的位置。
• Step 2. 接着再把左子树展开，放到相应位置。
• Step 3. 最后再把右子树展开，放到相应位置。此时就得到了最终前序遍历的结果。

不过你在处理根结点或者子树的时候，需要注意空树的情况。避免访问空指针！

递归前序遍历

基于以上思路，可以写出递归的前序遍历的代码（解析在注释里）：

void preOrder(TreeNode root, List<Integer> ans) {
if (root != null) {
        ans.add(root.val);
        preOrder(root.left, ans);
        preOrder(root.right, ans);
    }
}

代码：Java/C++/Python

接下来我们看一下算法的复杂度，在面试中经常有人将时间复杂度与空间复杂度混淆，这里很容易出错，你需要格外注意。

• 时间复杂度，由于树上的每个结点都只访问一次，并且每次访问都只有一次压栈弹栈操作，所以复杂度为 O(N)。
• 空间复杂度，由于函数调用栈的深度与树的高度有关系，所以使用的空间为 O(H)。H 表示树的高度。（注意：一般而言，输出结果存放的 List 并不算在空间复杂度里面）。

提示：在面试时候，你需要问清楚面试官：访问每个结点的时候，是需要 Print 出来，还是放到一个 List 里面返回。搞清楚需求再开始写代码！

使用栈完成前序遍历

接下来，我们看一下如何将递归的前序代码改成非递归的前序代码，如下所示（解析在注释里）：

class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
        Stack<TreeNode> s = new Stack<>();
        List<Integer> ans = new ArrayList<>();
while (root != null || !s.empty()) {
while (root != null) {
                s.push(root);
                ans.add(root.val);
                root = root.left;
            }
            root = s.peek();
            s.pop();
            root = root.right;
        }
return ans;
    }
}

代码：Java/C++/Python

算法复杂度：每个结点都入栈出栈一次，遍历整棵树的时间复杂度为 O(N)，空间复杂度就是栈的最大使用空间，而这个空间是由树的高度决定的，所以空间复杂度就是 O(H)。

备注：虽然面试的时候极难考到 Morris 遍历，如果你有时间，可以看看 Morris 遍历，这种算法的优点是只需要使用 O(1) 的空间（没有函数递归）。

代码：Java/C++/Python

下面我们通过几道题目还原一下面试场景，看看面试官都给你埋了哪些雷。

例 1：验证二叉搜索树

【题目】二叉搜索树有以下特点：

• 根结点的值大于所有的左子树结点的值
• 根结点的值小于所有的右子树结点的值
• 左右子树也必须满足以上特性

现给定一棵二叉树，判断是否是二叉搜索树。

输入:

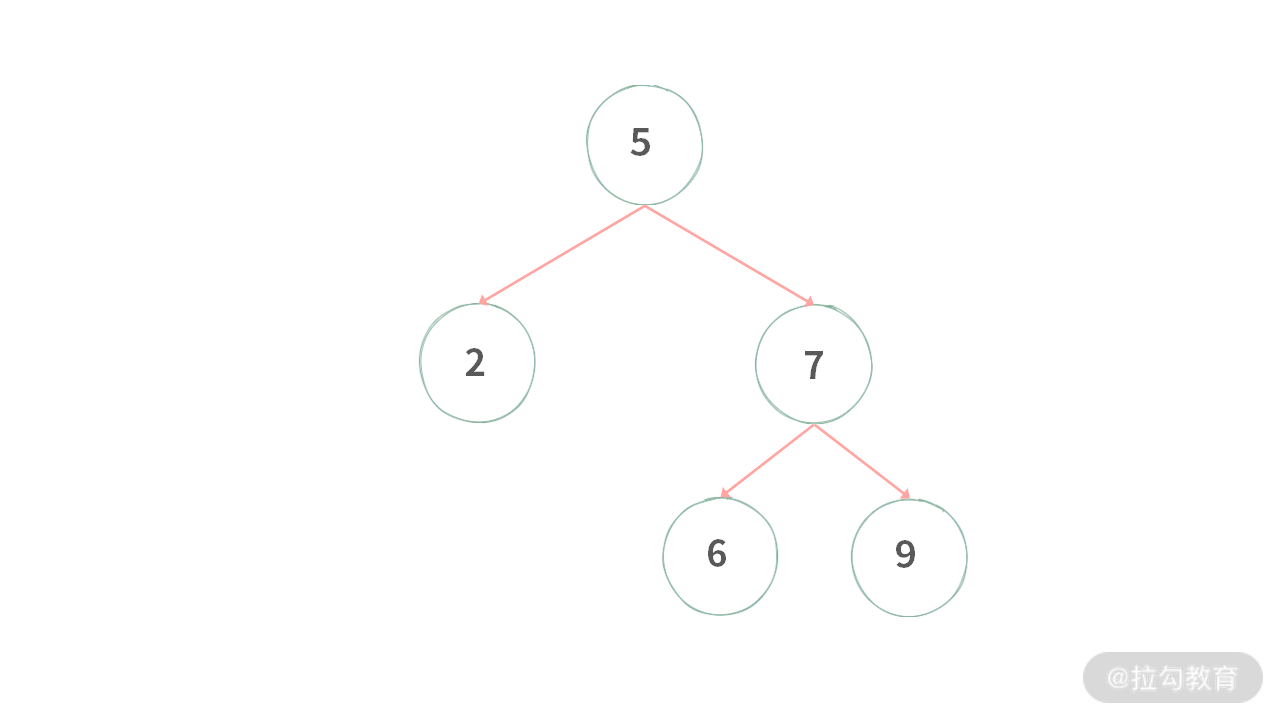
输出: true

【分析】二叉搜索树的定义，本质上就是一个前序遍历。因此，可以利用前序遍历的思路来解决这道题。

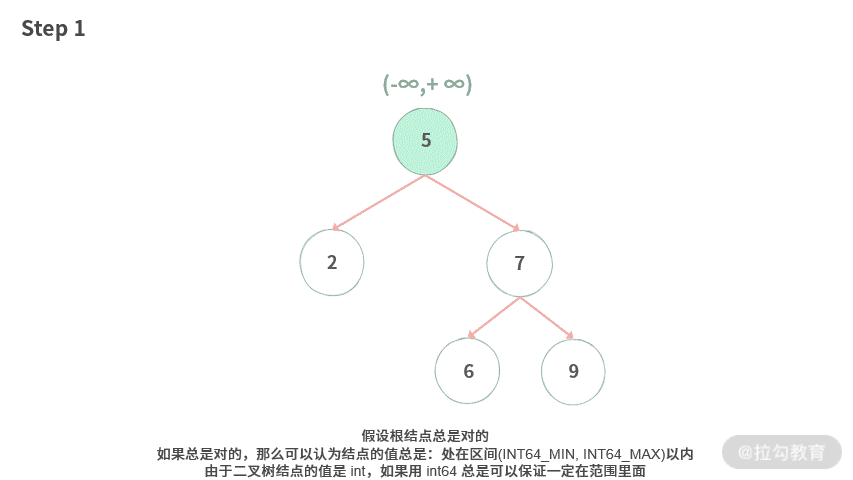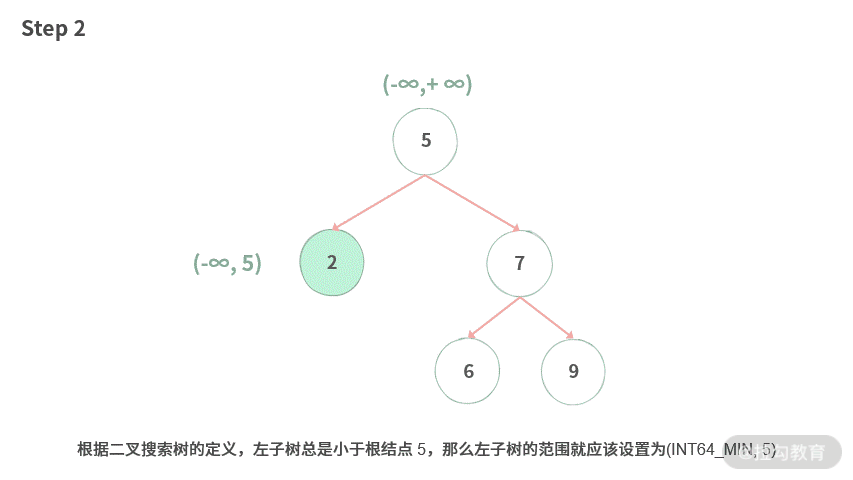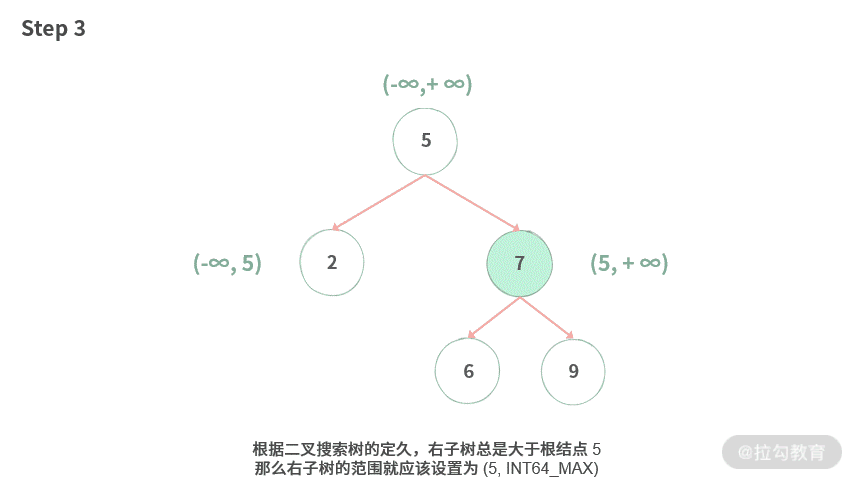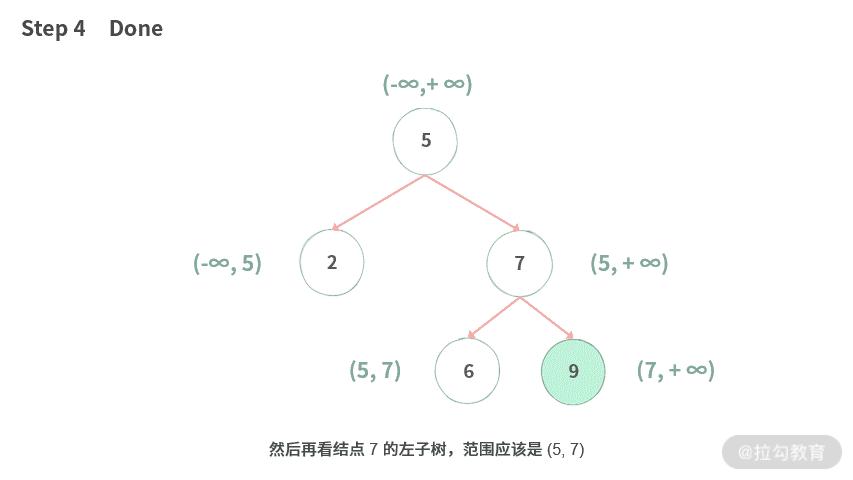
【模拟】首先我们在这棵树上进行模拟，效果如下 （用 INT64_MIN 表示负无穷大，INT64_MAX 表示正无穷大）：

Step 1. 我们假设根结点总是对的。如果总是对的，那么可以认为结点的值总是：处在区间 (INT64_MIN, INT64_MAX) 以内。由于二叉树结点的值是 int，如果用 int64 总是可以保证一定在范围里面。

Step 2. 根据二叉搜索树的定义，左子树总是小于根结点 5，那么左子树的范围就应该设置为 (INT64_MIN, 5)。

Step 3. 根据二叉搜索树的定久，右子树总是大于根结点 5，那么右子树的范围就应该设置为 (5, INT64_MAX)。

Step 4. 然后再看结点 7 的左子树，范围应该是 (5, 7)。

【规律】经过运行的模拟，我们可以总结出以下特点：

• 通过原本给出的那棵二叉树，实际上能够构造出一棵 “影子”区间二叉树，只不过这个二叉树上的结点是一个区间；
• 原二叉树上的值，需要掉在新二叉树的区间范围里面。

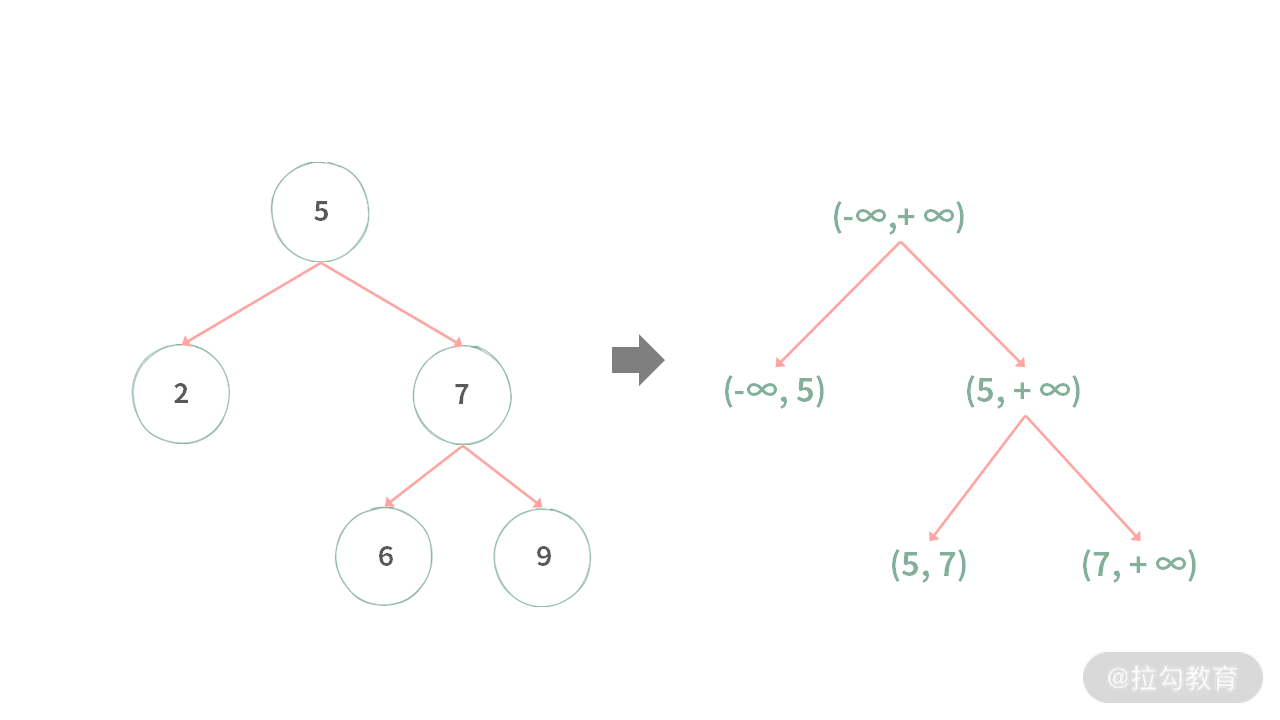
因此，解题的思路就是：

• 如何有效利用右边的 “区间” 二叉树验证左边二叉树的有效性？
• 当右边的 “区间” 二叉树不能成功构建，原二叉树就是一棵无效的二叉搜索树。

注：我们不是真的要构建 “影子” 二叉树，这样做的目的是方便思考。

“影子” 二叉树是通过原二叉树生成的。树上结点就是不停地将区间进行拆分，比如：

• (INT64_MIN, INT64_MAX) -> (INT64_MIN, 5) , (5, INT64_MAX)
• (5, INT64_MAX) -> (5, 7), (7, INT64_MAX)

【匹配】我们就利用二叉树的前序遍历，同时遍历这两棵二叉树。注意，其中 “影子” 二叉树是动态生成的，并且我们也不保存其数据结构。

【边界】关于二叉树的边界，我们需要考虑一种情况：

• 一棵空二叉树；
• 题目的定义采用的 “小于”，“大于”；
• 当任何一个位置不满足二叉树的定义，就可以不用再遍历下去了。因此，我们要注意快速返回。

【代码】 有了思路，也有了运行图，此时就可以写出以下核心代码（解析在注释里）：

class Solution {
private boolean ans = true;
private void preOrder(TreeNode root, Long l, Long r) {
if (root == null || !ans) {
return;
        }
if (!(l < root.val && root.val < r)) {
            ans = false;
return;
        }
        preOrder(root.left, l, Long.valueOf(root.val));
        preOrder(root.right, Long.valueOf(root.val), r);
    }
public boolean isValidBST(TreeNode root) {
        ans = true;
        preOrder(root, Long.MIN_VALUE, Long.MAX_VALUE);
return ans;
    }
}

代码：Java/C++/Python

【小结】我们在传统经验的前序遍历基础上，进行了一点扩展，需要创建一棵 “影子” 二叉树才能进行前序遍历。因此这道题的考点就是：找到隐藏的 “影子” 二叉树。

此外，遍历二叉树的时候，如果可以用递归，那么应该也可以用栈，或者 Morris 遍历。作为一道思考题，你能用栈来完成 “验证二叉搜索树” 这道题目吗？

代码：Java/C++/Python

为了巩固我们前面所讲的知识，下面我再给你留两道练习题。

练习题 1：“影子” 二叉树还可以解决 “是否相同的树” 的问题。比如给定两棵二叉树，要求判断这两棵二叉树是不是一样的？思考的时候，再想一下，“影子” 二叉树是怎么样的呢？

代码：Java,C++,Python

当然，有时候出题人还会将一些考点进行组合，比如将 “相同的子树” 与 “前序遍历” 进行组合，就可以得到一道新的题目。

练习题 2：当我们写出 “判断是否相同的树” 的代码之后，可以开始思考另外一个问题——如何判断一棵树是不是另外一棵树的子树？

代码：Java/C++/Python

你可以把答案或者思考的过程写在评论区，我们一起讨论。

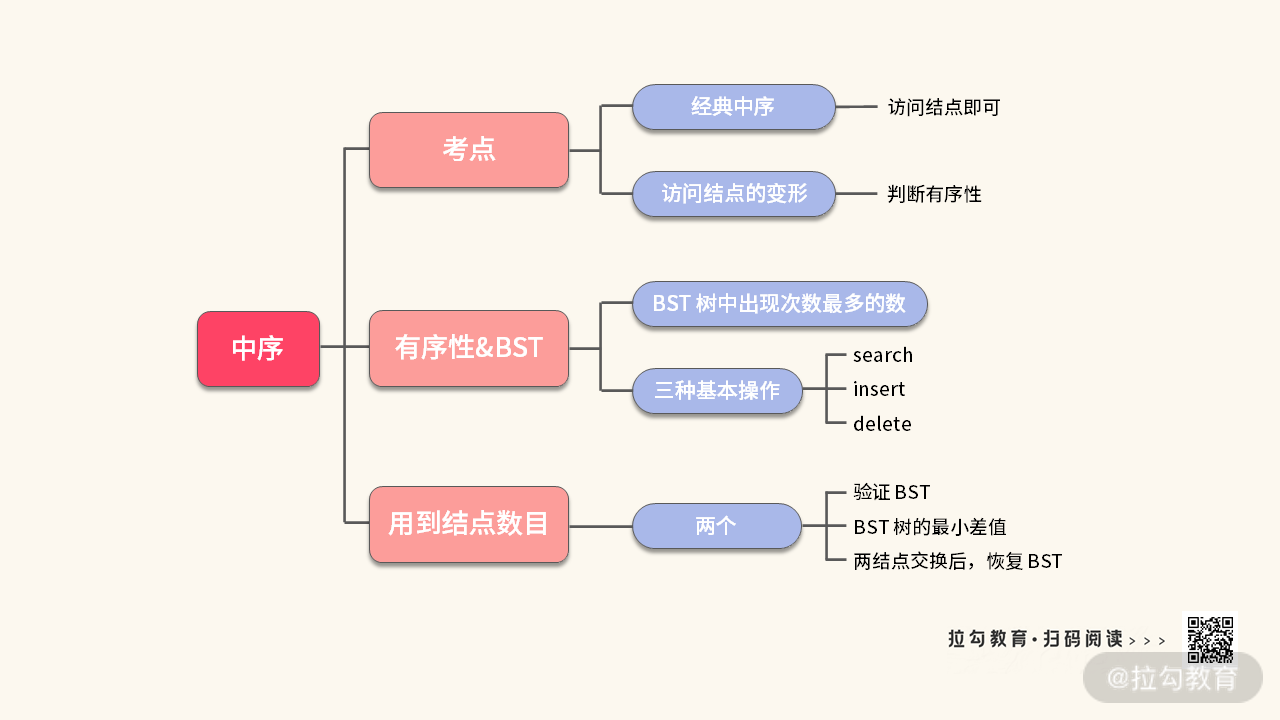
到这里，我们可以总结一下解题时用到的知识点和收获。为了方便你理解和复习，我把关于 “树的遍历” 的考点整理在一张大图里，如下图所示：

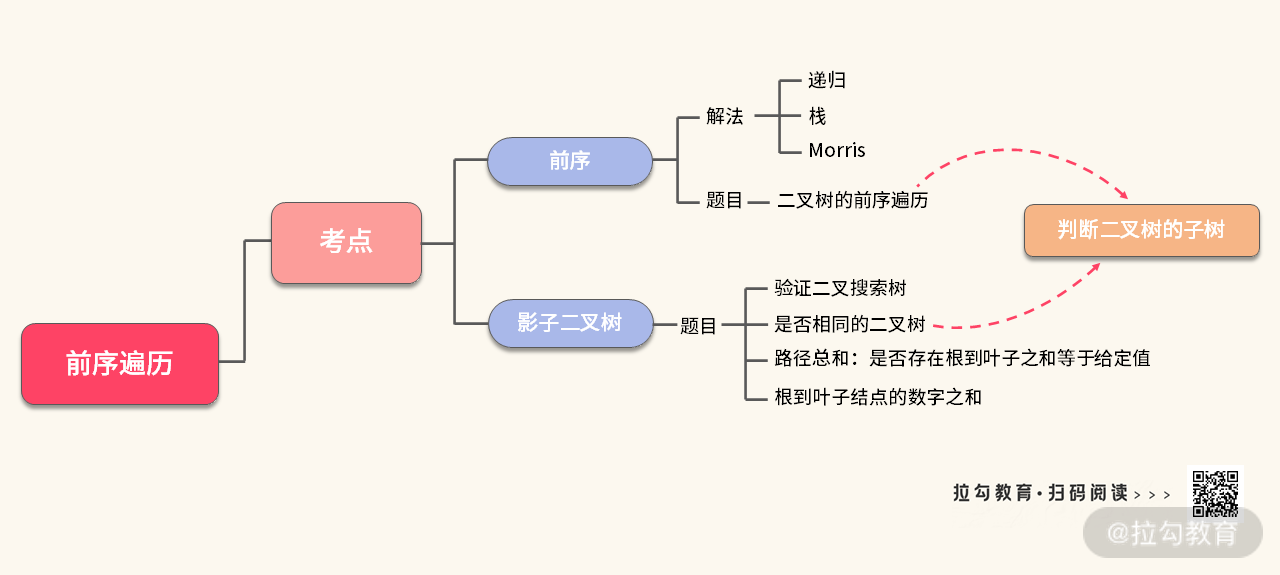
然后，我们收获了一种思路——“影子” 二叉树；一个模板——如何判断相同的树。

例 2：目标和的所有路径

【题目】给定一棵二叉树，一个目标值。请输出所有路径，需要满足根结点至叶子结点之和等于给定的目标值。

输入：target = 9

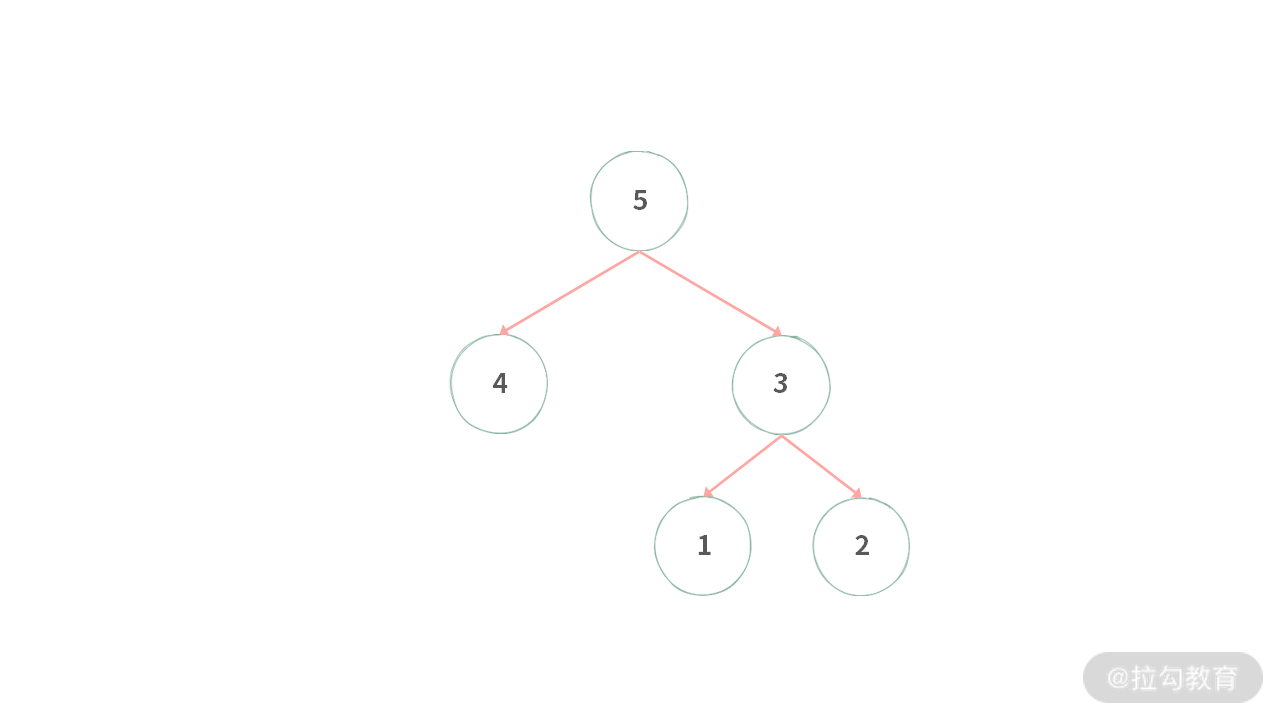
输出：[[5,4], [5,3,1]]

解释：从根结点到叶子结点形成的路径有 3 条：[5, 4], [5, 3, 1], [5, 3, 2]，其中只有 [5, 4], [5, 3, 1] 形成的和为 9。

【分析】这是一道来自头条的面试题目。首先题目要求从根结点出发，最后到达叶子结点。因此，从遍历的顺序上来说，符合前序遍历。

【模拟】那么接下来我们进行一轮模拟，过程如下所示：

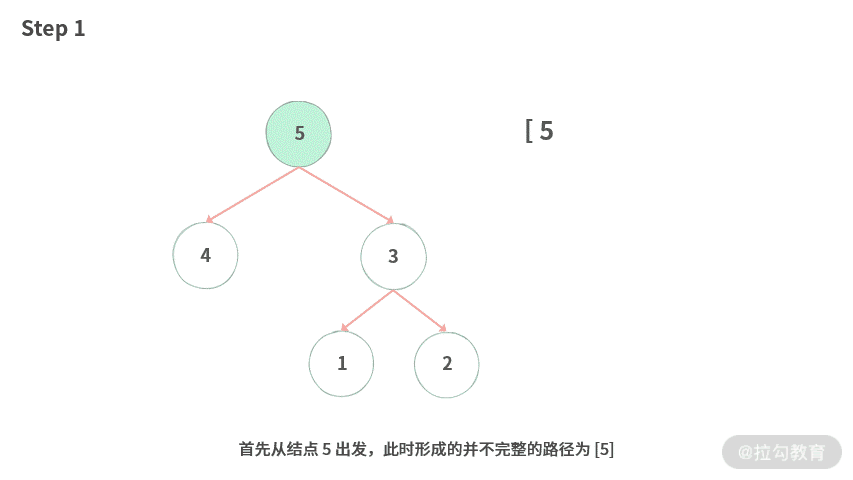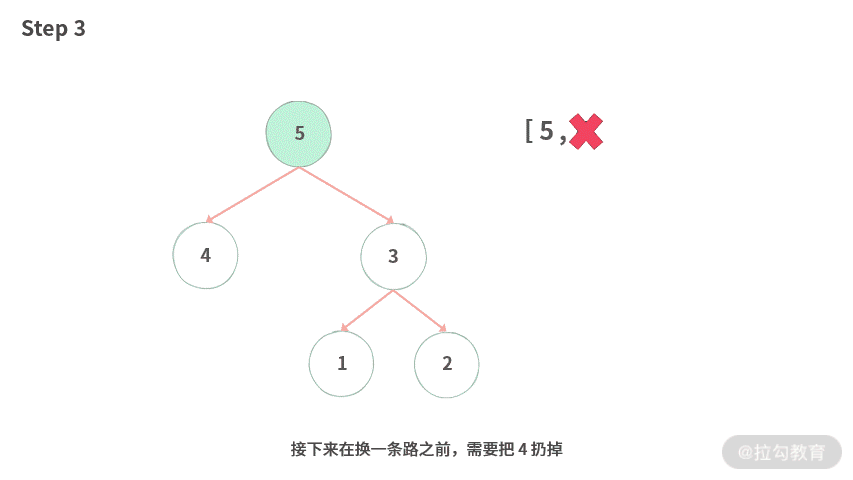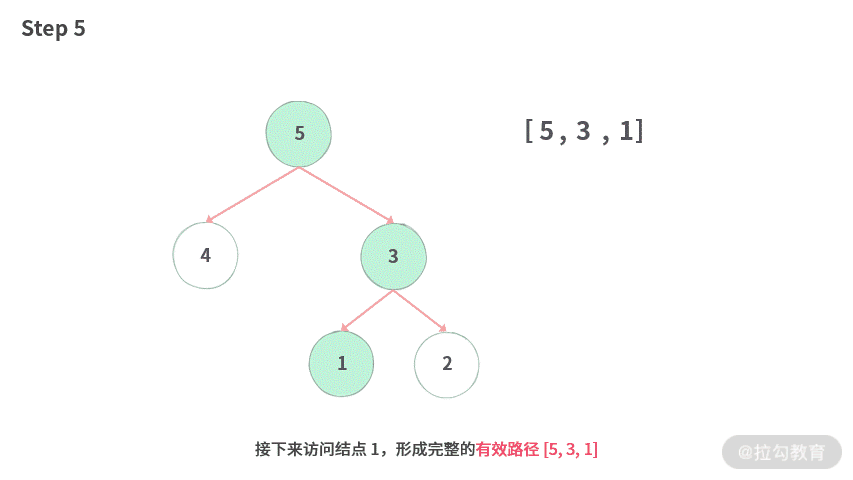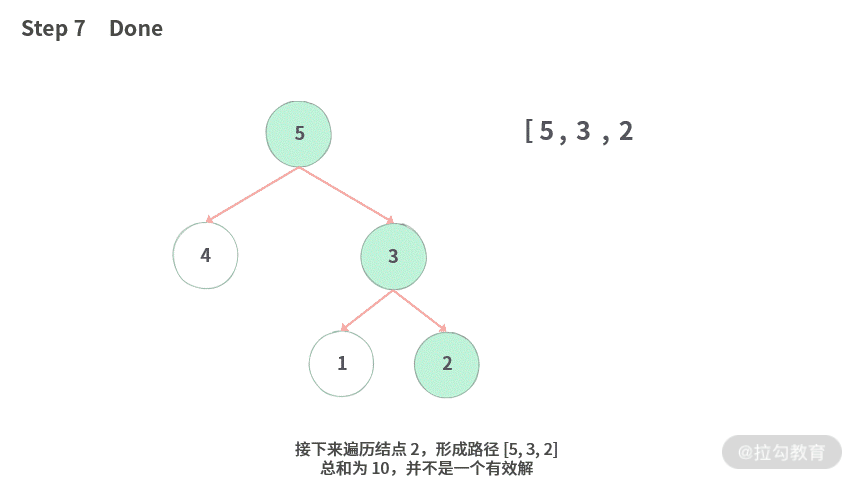
Step 1. 首先从结点 5 出发，此时形成的并不完整的路径为 [5]。

Step 2. 接着走向左子结点 4，形成一个有效路径 [5, 4]。

Step 3. 接下来在换一条路之前，需要把 4 扔掉。

Step 4. 按照前序遍历顺序访问 3，形成并不完整的路径 [5, 3]。

Step 5. 接下来访问结点 1，形成完整的有效路径 [5, 3, 1]。

Step 6. 当结点 1 遍历完之后，需要从路径中扔掉。

Step 7. 接下来遍历结点 2，形成路径 [5, 3, 2]。总和为 10，并不是一个有效解。

因此，我们一共找到两个有效解 [5, 4], [5, 3, 1]。

【规律】经过模拟的过程，可以发现了以下特点：

• 遇到新结点，路径总是从尾部添加结点；
• 遍历完结点，路径就把它从尾部扔掉；

路径里面的元素刚好与递归时压栈的元素完全一样。因此，我们需要在递归结束时，把路径里面的元素像 “弹栈” 一样扔掉。

【匹配】基于二叉树而言，这里的考点当然是前序遍历。但是我们发现：还需要另外一个信息 “路径”：随着参数的压栈、弹栈而变化。

【边界】按照题意，这里需要注意两点：

• 题目一定要根结点到叶子结点
• 注意代码要支持空树

【代码】此时，我们已经可以写一写代码了（解析在注释里）：

class Solution {
private List<List<Integer>> ans = new ArrayList<>();
private void backtrace(TreeNode root, 
      List<Integer> path, int sum, int target) {
if (root == null) {
return;
        }
        sum += root.val;
        path.add(root.val);
if (root.left == null && root.right == null) {
if (sum == target) {
                ans.add(new ArrayList<>(path));
            }
        } else {
            backtrace(root.left, path, sum, target);
            backtrace(root.right, path, sum, target);
        }
        path.remove(path.size()-1);
    }
public List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<Integer> path = new ArrayList<>();
        backtrace(root, path, 0, sum);
return ans;
    }

代码：Java/C++/Python

复杂度分析：首先遍历每个结点，复杂度肯定是 O(N)。但是最大的复杂度在于复制有效路径。假设有一棵满二叉树，最下面一层结点都符合要求。那么一共需要复制 N/2 次。而每次需要复制路径深度为 log(N)。因此，复杂度为 N/2 * log(N)，即 NlgN。

【小结】本质上，这道题的考点就是：回溯，只不过借用了二叉树这个皮。反过来，在二叉树上进行回溯的代码模板，你也需要熟练掌握。

如果我们把题目中 “路径之和等于 target” 这个条件去掉，那么题目就变成了需要输出二叉树到叶子结点的所有路径。想必这道题目你也能够解决了吧？

到这里，我们又可以进一步丰富了前面总结出的关于 “二叉树的前序遍历” 的思维导图了，如下图所示：

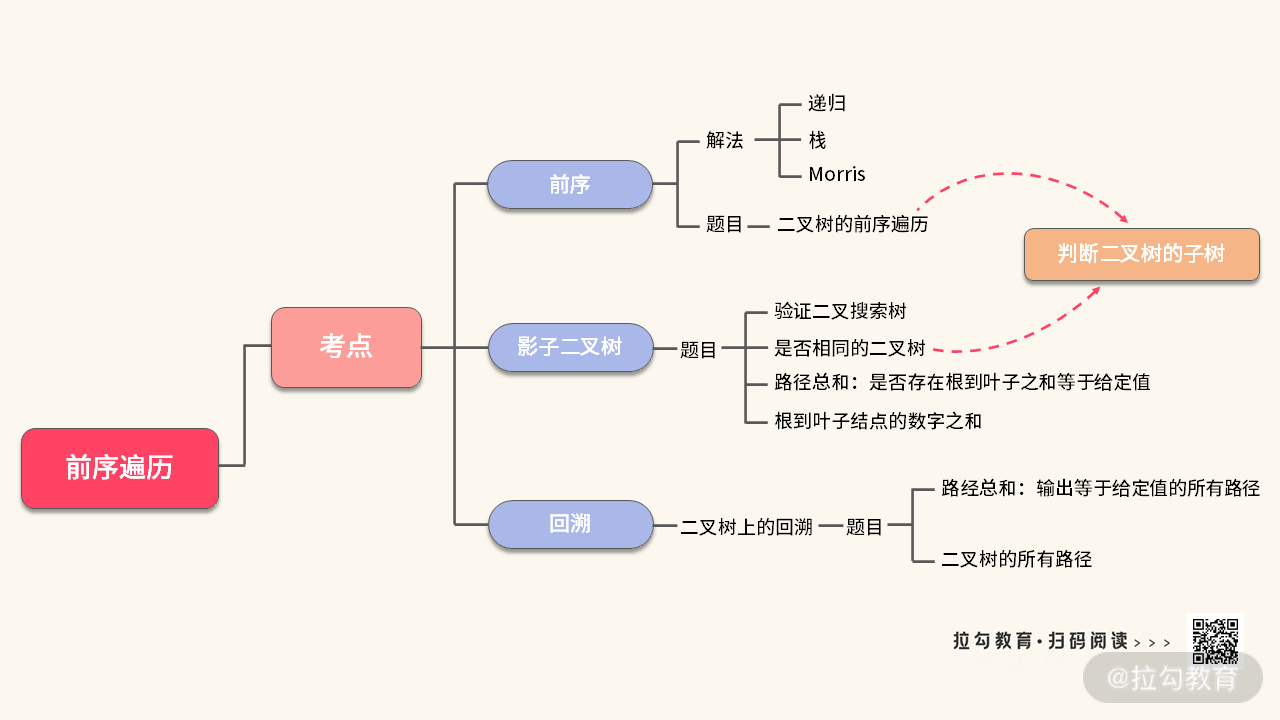
在这里，我们收获了：二叉树上的回溯模板。

前序遍历的变种还有很多，结合不同的考点，还会有新的题型出现，但是只要我们能分析出题目的考点，有效地掌握一些代码模板进行相互组合，一定能克服这些新鲜的题目。

中序遍历

接下来我们看一下中序遍历。中序遍历的顺序：

1. 左子树
2. 根结点
3. 右子树

这里不再按照课本上一步一步演示的方式，同样可以采用一种概括处理的思路，如下所示：

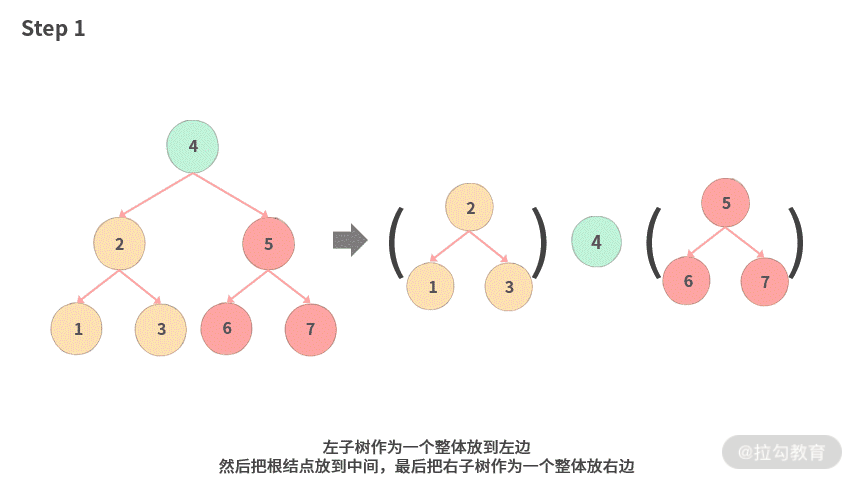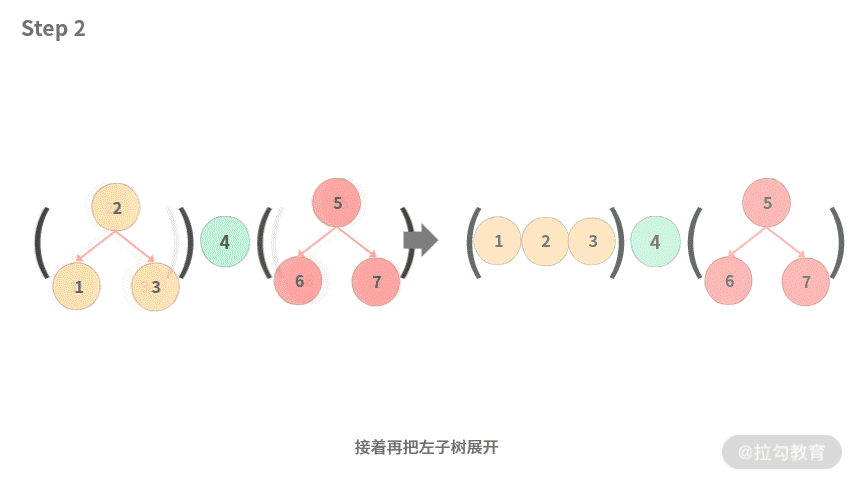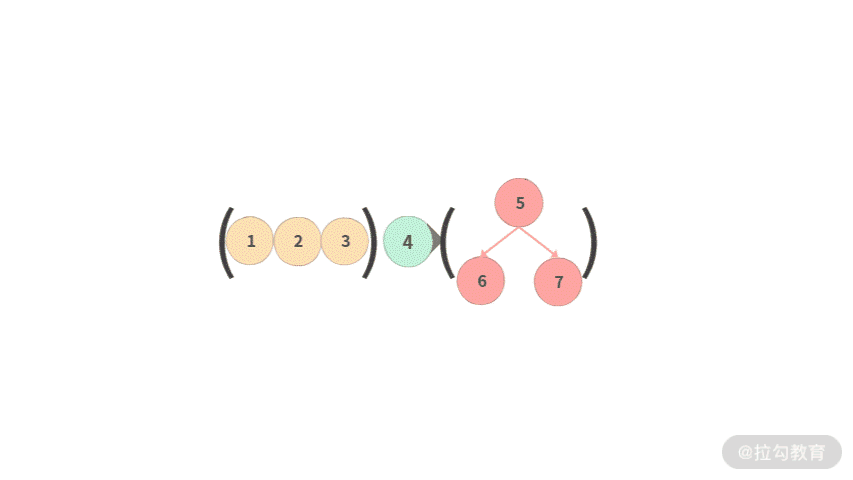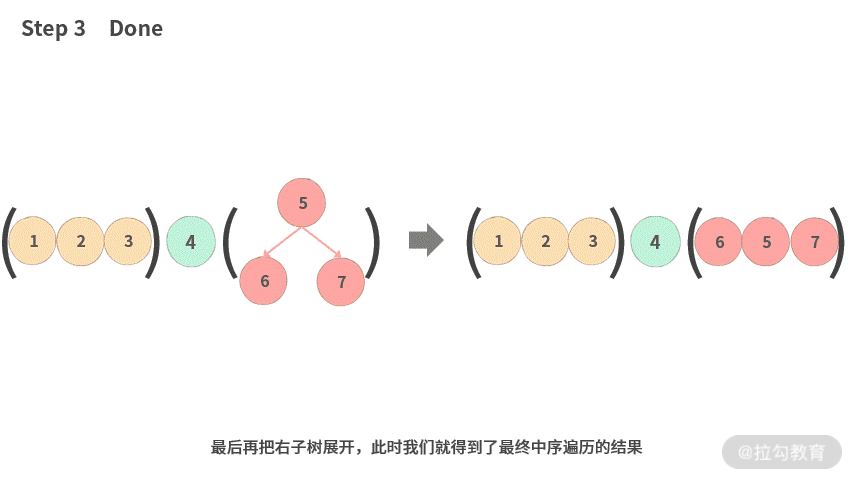
• Step 1. 左子树作为一个整体放到左边；然后把根结点放到中间；最后把右子树作为一个整体放右边。
• Step 2. 接着再把左子树展开。
• Step 3. 最后再把右子树展开，此时我们就得到了最终中序遍历的结果。

经过上述过程的拆解和分析，有助于帮助你理解中序遍历。但是仍然要注意输出结点的顺序，结点真正输出顺序如下图所示：

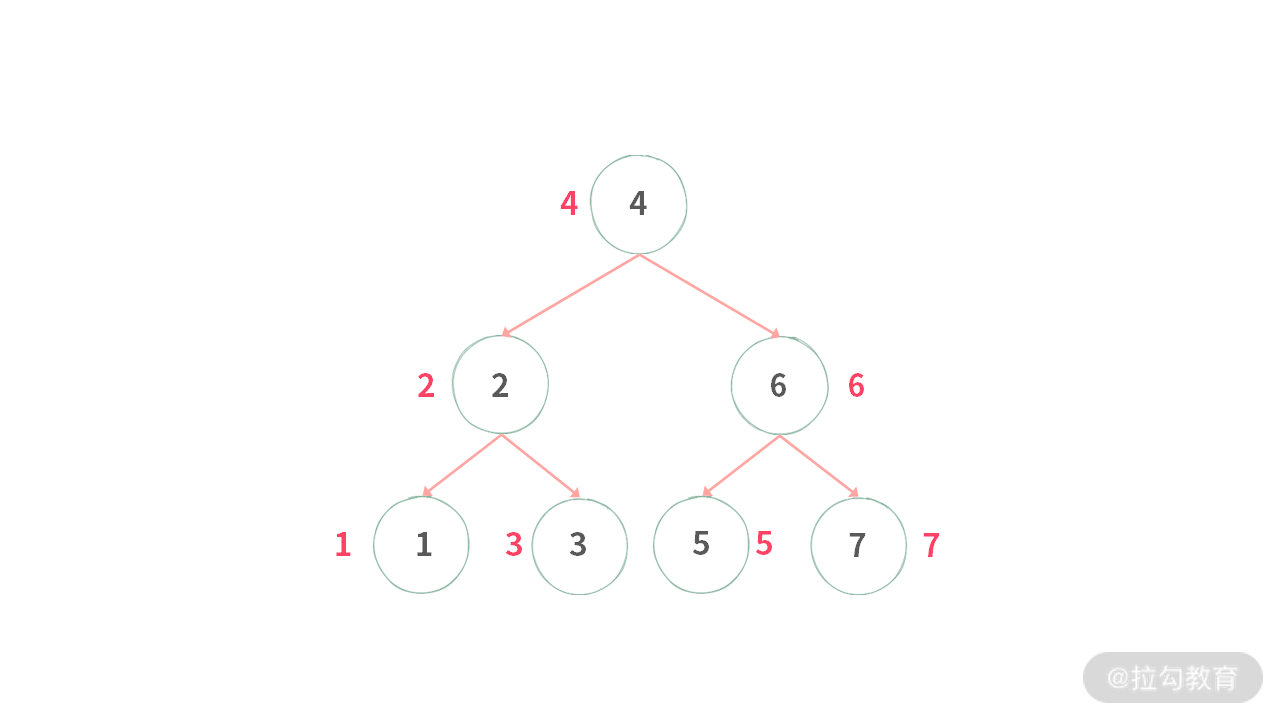
递归中序遍历

基于以上思路，我们可以写出递归的中序遍历的代码（解析在注释里）：

void preOrder(TreeNode root, List<Integer> ans) {
if (root != null) {
        preOrder(root.left, ans);
        ans.add(root.val);
        preOrder(root.right, ans);
    }
}

代码：Java/C++/Python

复杂度分析：时间复杂度为 O(N)，每个结点都只遍历一次，并且每个结点访问只需要 O(1) 复杂度的时间。空间复杂度为 O(H)，其中 H 为树的高度。

使用栈完成中序遍历

接下来，我们看一下如何将递归的中序代码，改成非递归的中序代码（解析在注释里）：

class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> s = new Stack<>();
        List<Integer> ans = new ArrayList<>();
while (root != null || !s.empty()) {
while (root != null) {
                s.push(root);
                root = root.left;
            }
            root = s.peek();
            s.pop();
            ans.add(root.val);
            root = root.right;
        }
return ans;
    }
}

代码：Java/C++/Python

复杂度分析：时间复杂度为 O(N)，每个结点都只遍历一次，并且每个结点访问只需要 O(1) 复杂度的时间。空间复杂度为 O(H)，其中 H 为树的高度。

备注：虽然面试的时候极难考到 Morris，但如果你想多掌握一种解题方法，可以尝试用 Morris 遍历，其优点是只需要使用 O(1) 的空间复杂度。这里我先给出完整实现代码，如有你有疑问可以写在留言区，我们一起讨论。

代码：Java/C++/Python

例 3：验证二叉搜索树

【题目】（与例 1 一样）给定一棵二叉树，要求验证是不是一棵二叉搜索树。

【分析】根据二叉搜索树的特性，可以知道。中序遍历一定有序。因此，可以利用这个特性进行验证。如果从这个角度来切入，那么题目的考点就可以总结如下：

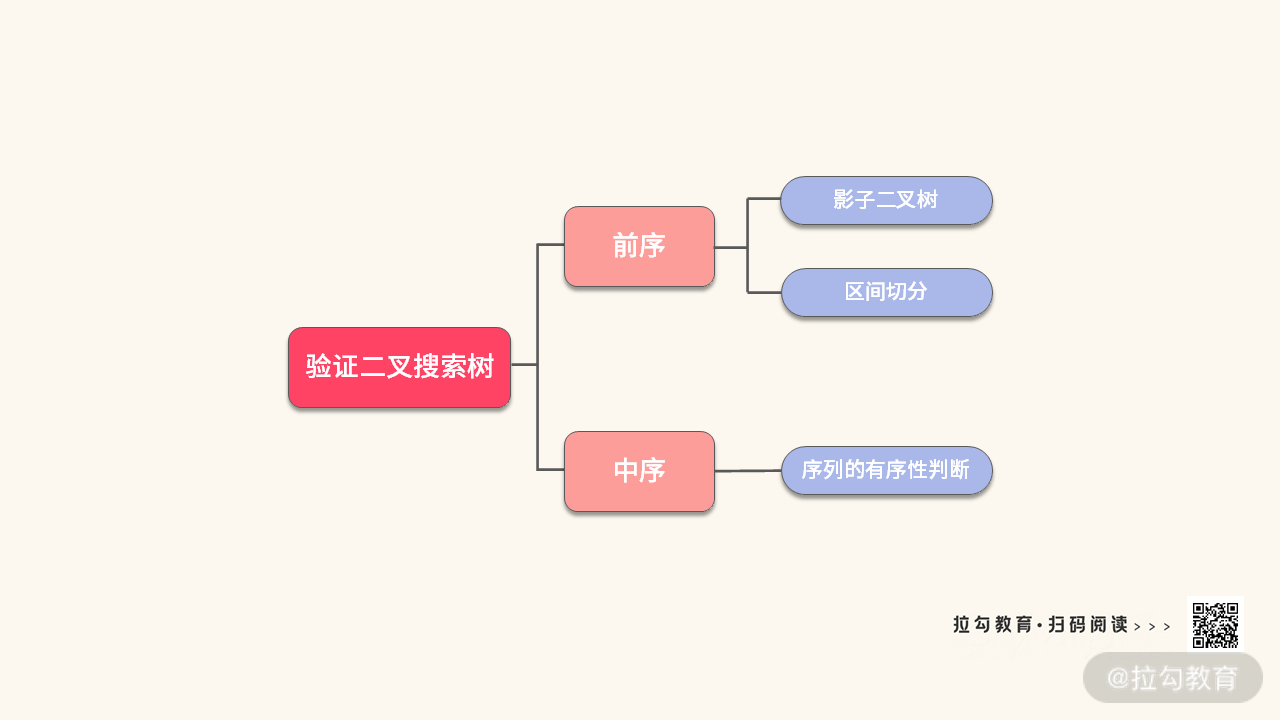
接下来我们就尝试用中序遍历解决这道题目，代码如下（解析在注释里）：

class Solution {
boolean ans = true;
    Long preValue = Long.MIN_VALUE;
private void midOrder(TreeNode root) {
if (!ans) {
return;
        }
if (root != null) {
            midOrder(root.left);
if (preValue >= root.val) {
                ans = false;
return;
            }
            preValue = Long.valueOf(root.val);
            midOrder(root.right);
        }
    }
public boolean isValidBST(TreeNode root) {
        ans = true;
        preValue = Long.MIN_VALUE;
        midOrder(root);
return ans;
    }
}

代码：Java/C++/Python

复杂度分析：时间复杂度 O(N)，每个结点只遍历一次，并且每个结点访问只需要 O(1) 时间复杂度。空间复杂度为 O(H)，其中 H 为树的高度。

【小结】平时练习的时候，你不妨将同类型的二叉树题目串起来进行比较，也许会发现题目真正的考点。比如将 “二叉树的中序遍历” 与 “验证二叉搜索树” 这两类题目放在一起思考，就会发现，考点是将中序遍历访问结点时候的处理做了一点小小的变化。

另外，在处理二叉搜索树的时候，还需要利用有序性。中序遍历二叉搜索树的时候，可以把它看成一个有序的数组，在此基础上展开思路。

练习题 3：找出二叉搜索树里面出现次数最多的数。

代码：Java/C++/Python

我们还可以做进一步思考。经典的中序遍历只访问了一个结点，关心一个结点的性质。而 “验证二叉搜索树” 需要访问两个结点，用两个结点的信息做决策。

因此，从 “需要用的结点个数” 角度出发，也可以衍生出一些题目。这里给你留两道练习题，帮助你巩固前面所讲的知识，希望你可以在课下完成它。

练习题 4：找出二叉搜索树任意两结点之间绝对值的最小值

代码：Java/C++/Python

练习题 5：一棵二叉搜索树的两个结点被交换了，恢复这棵二叉搜索树

解法 1（递归）：Java/C++/Python
解法 2（栈）：Java/C++/Python
解法 3（Morris）：Java/C++/Python

至此，我们已经挖掘了中序遍历可能的考点，如下图所示：

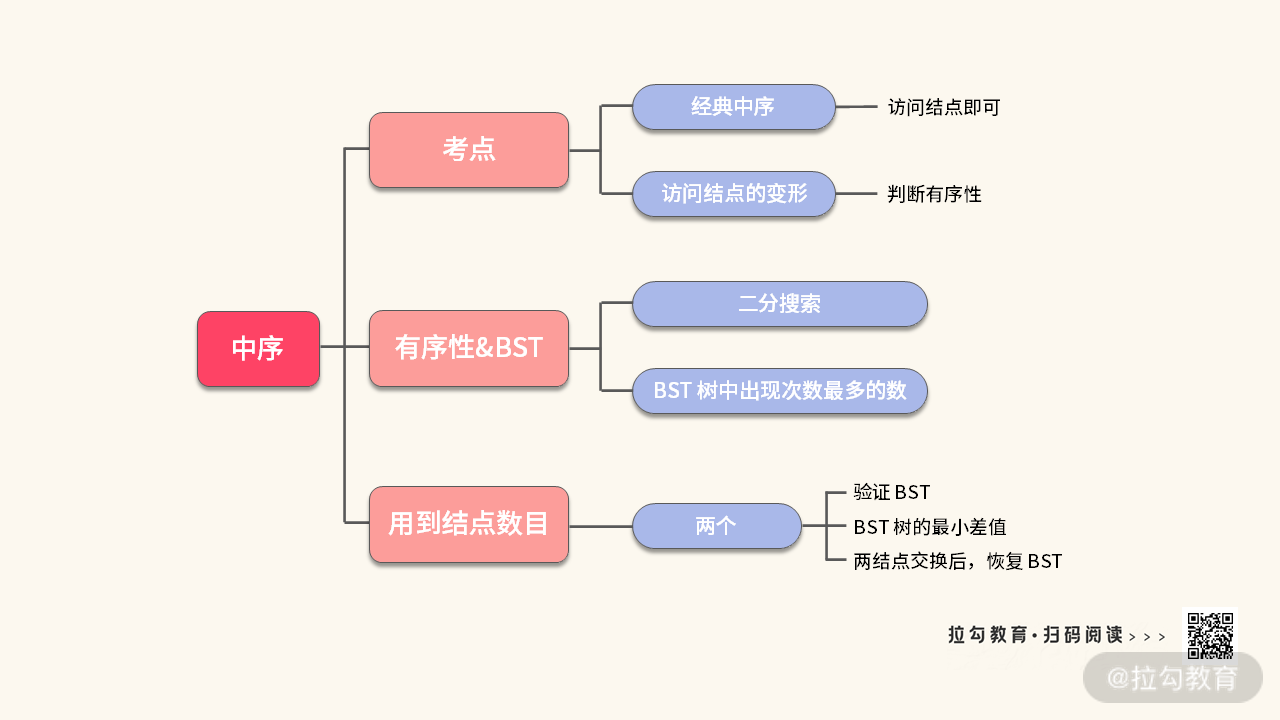
讲完二叉搜索树（BST），我们再来看看 “如何删除二叉搜索树的结点”，这也是面试中很重要的一个考点。

例 4：删除二叉搜索树的结点

【题目】删除二叉搜索树的指定结点。返回删除之后的根结点。接口如下：

TreeNode deleteNode(TreeNode root, int value);

【分析】这是一道来自微软的面试题。它的难点在于需要考虑各种情况。因此，针对这道题的题目特点，我们把重点放在分析各种 Case。

Case 1：空树。如果树是空树，那么只需要返回 null 即可。

Case 2：如果 value 比根结点小，那么去左子树里面删除相应结点，执行：

if (value < root.val) {
    root.left = deleteNode(root.left, value);
}

这里只有一行核心代码，但却非常有意思。因为这行代码统一处理了以下几种情况。

a）当结点 1 删除之后，左子树为空，需要设置 root.left = null。如下图所示：

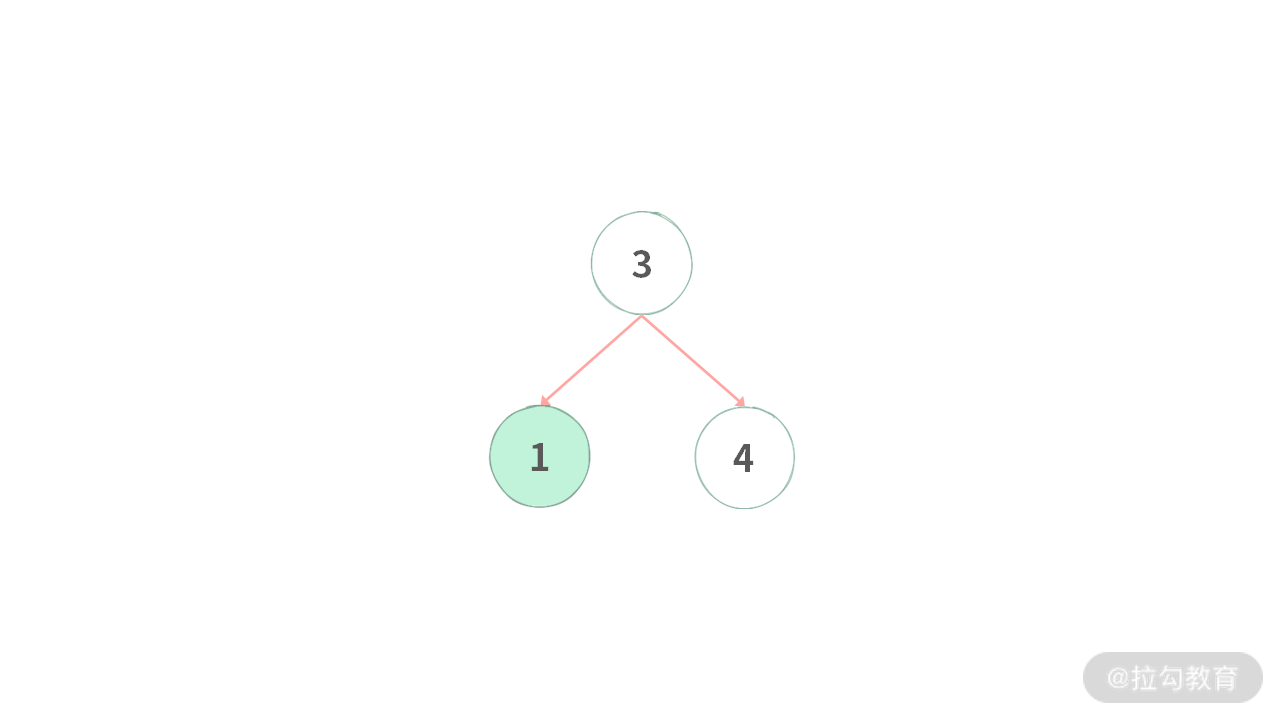
b）当结点 1 删除之后，左子树的根结点为 2，需要设置 root.left 指向结点 2。如下图所示：

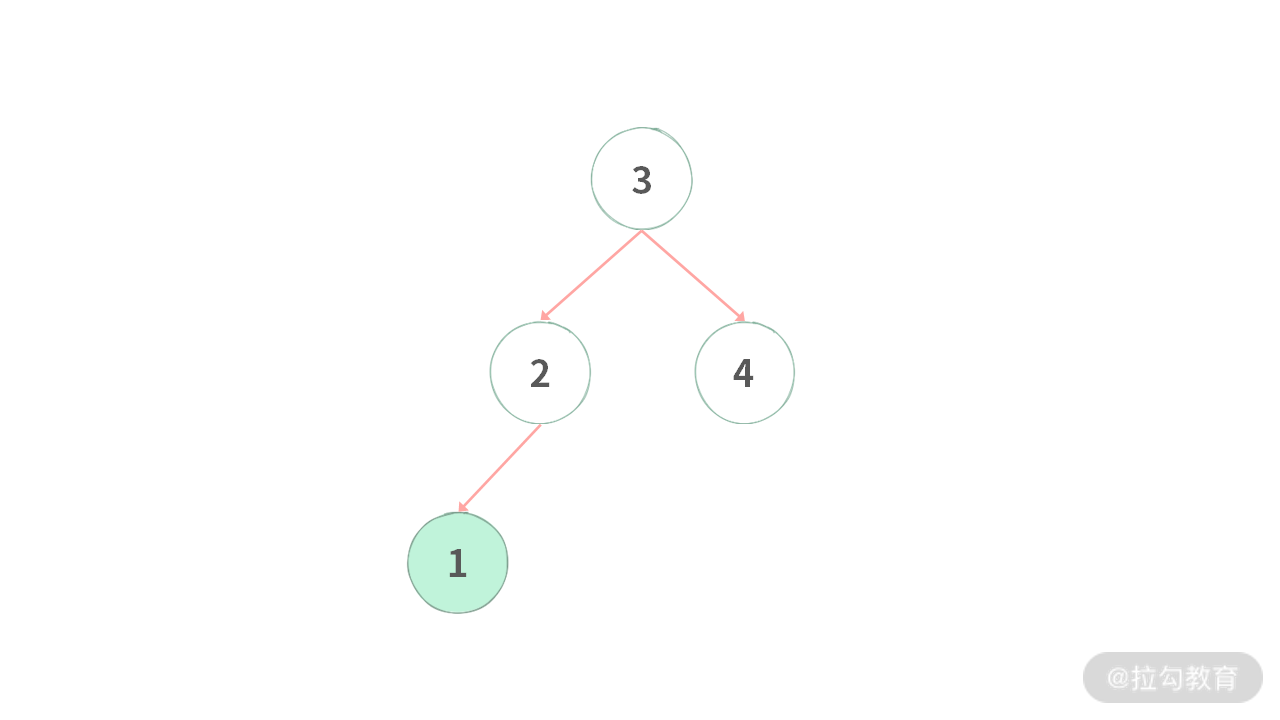
c）当结点 1 删除之后，左子树根结点变成 2，需要设置 root.left 指向结点 2。如下图所示：

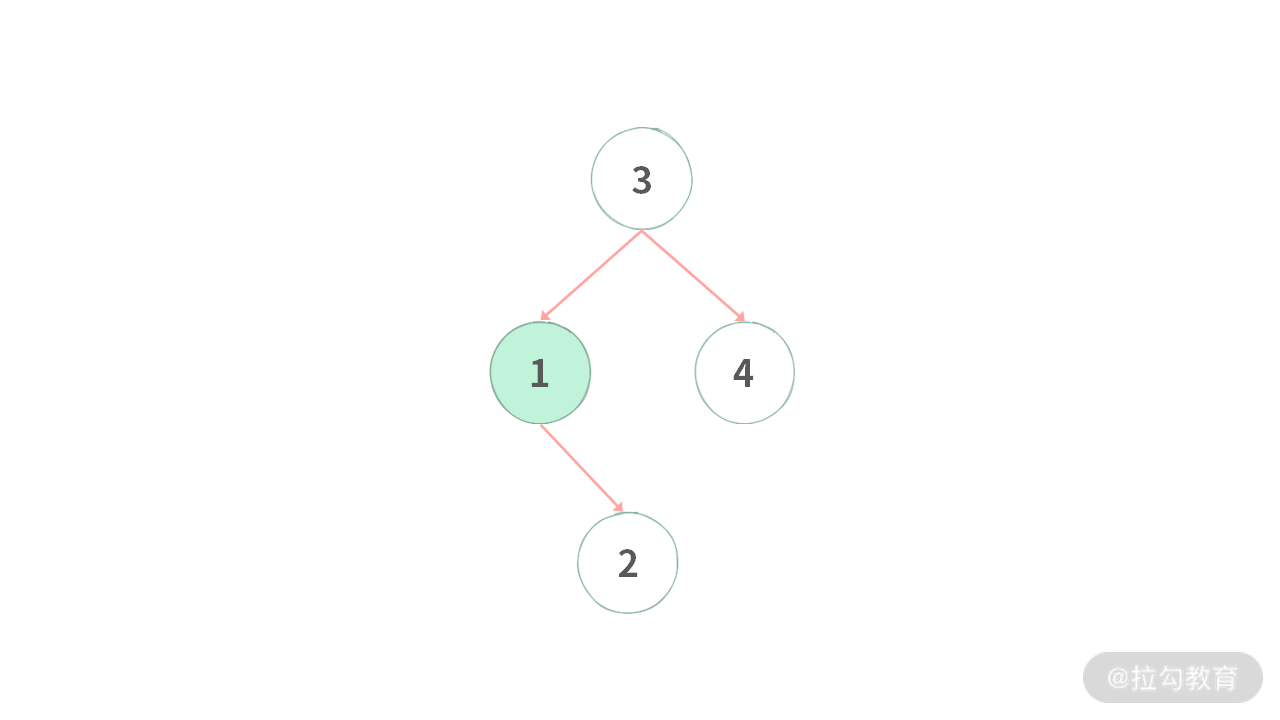
因此，删除结点时，需要：

root.left = deleteNode(root.left, value);
或
root.right = deleteNode(root.right, value);

虽然看起来 b）没有重新赋值的必要，但是利用这一句话，却把 a）、b）、c）三情况都统一起来了。我们再思考时，就不需要考虑更多的情况了。

Case 3：如果 value 比根结点大，那么需要执行：

if (value > root.val) {
    root.right = deleteNode(root.right, value);
}

Case 4：如果 value 与根结点的值相等，那么需要再分四种情况考虑。

a）此时只有一个结点。比如：

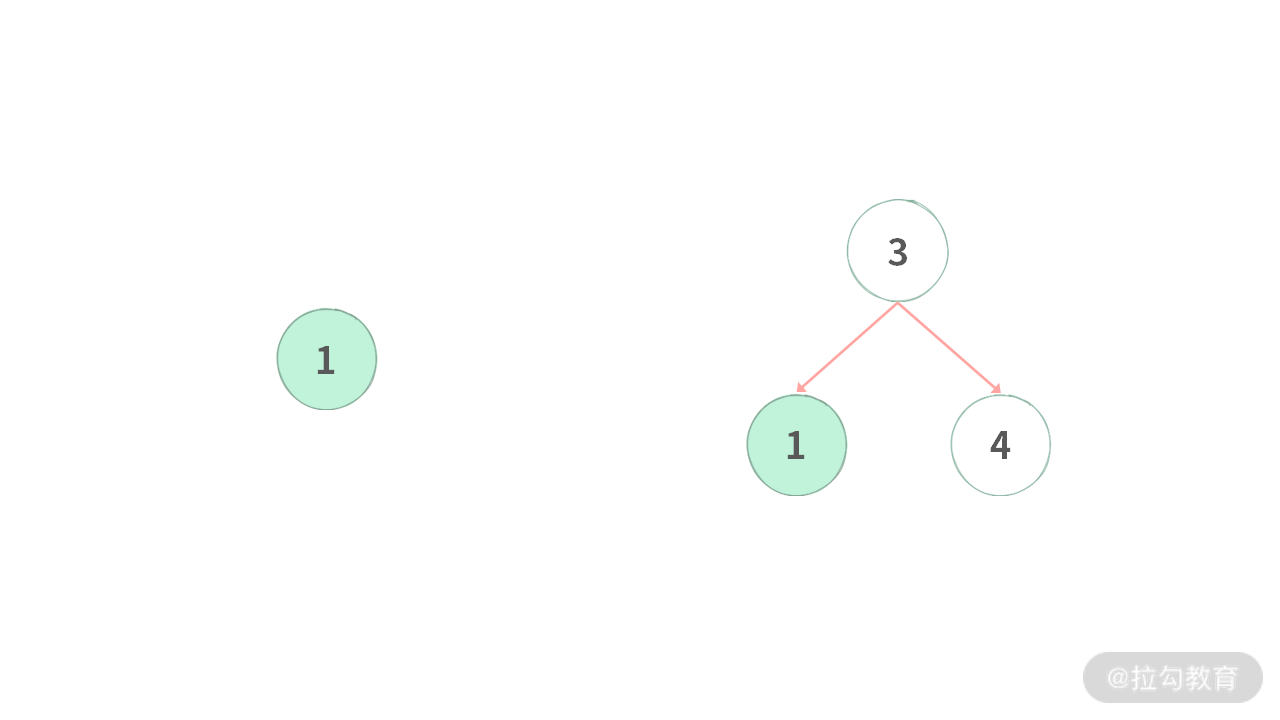
在删除 1 之后，都需要返回 null。

b）如果被删除的结点有左子树。那么需要从左子树中找到最大值，然后与当前结点进行值交换。最后再在左子树中删除 value。步骤如下：

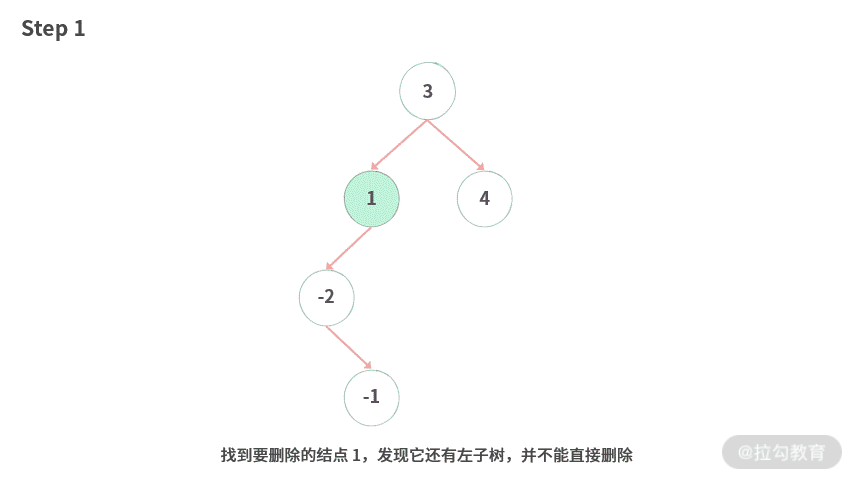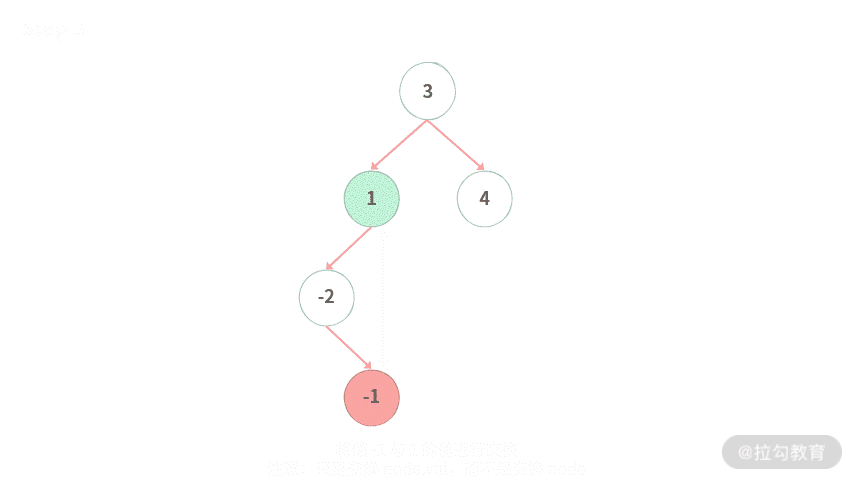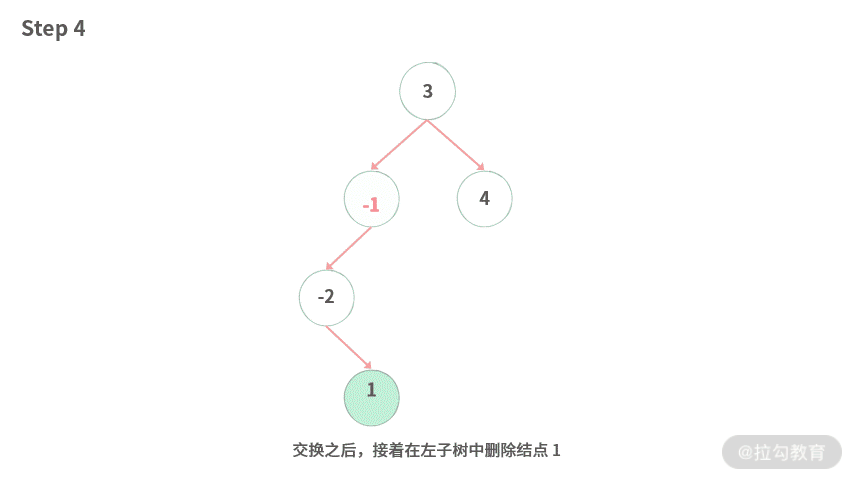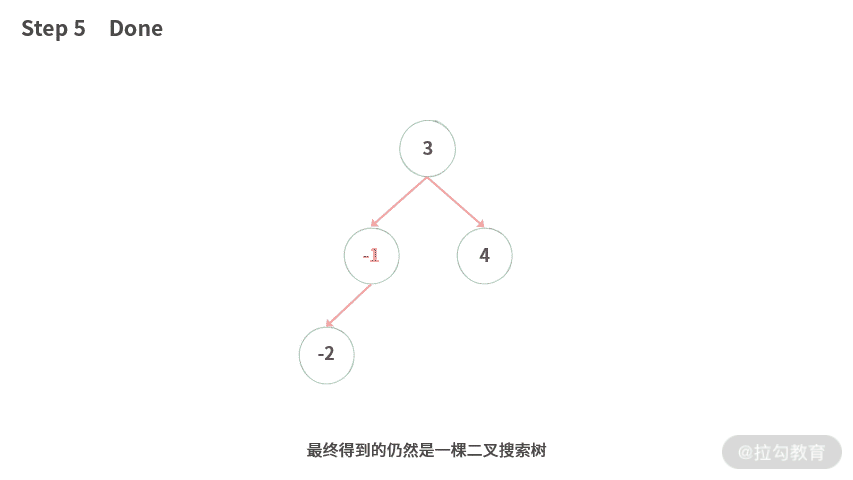
Step 1. 找到要删除的结点 1，发现它还有左子树。并不能直接删除。

Step 2. 找到左子树里面的最大值 -1。

Step 3. 将值 -1 与 1 的值进行交换。注意：我们只是交换 node.val，而不是交换 node。

Step 4. 交换之后，接着在左子树中删除结点 1。

Step 5. 最终得到的仍然是一棵二叉搜索树。

c）如果要删除的结点只有右子树。那么需要从右子树中找到最小值，然后与当前结点进行值交换。然后再在右子树中删除 value。步骤如下：

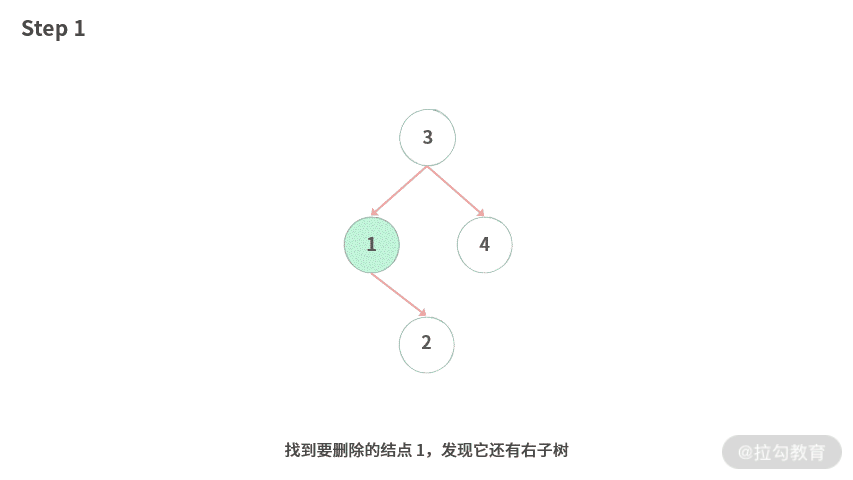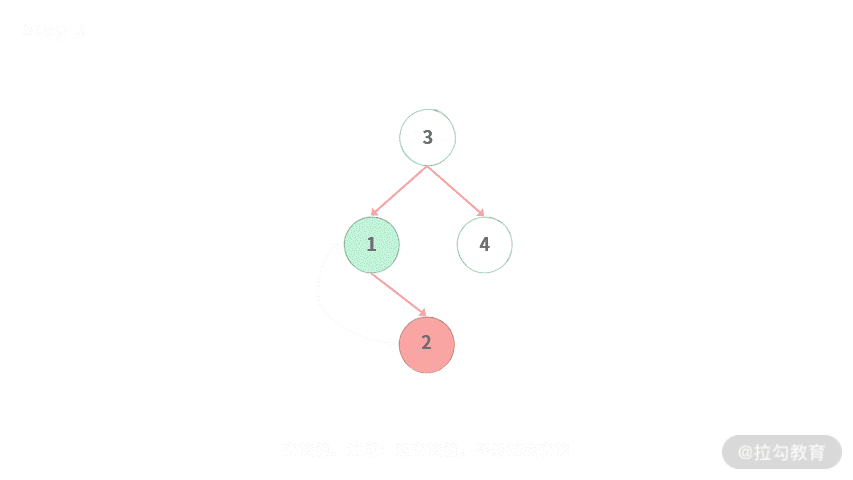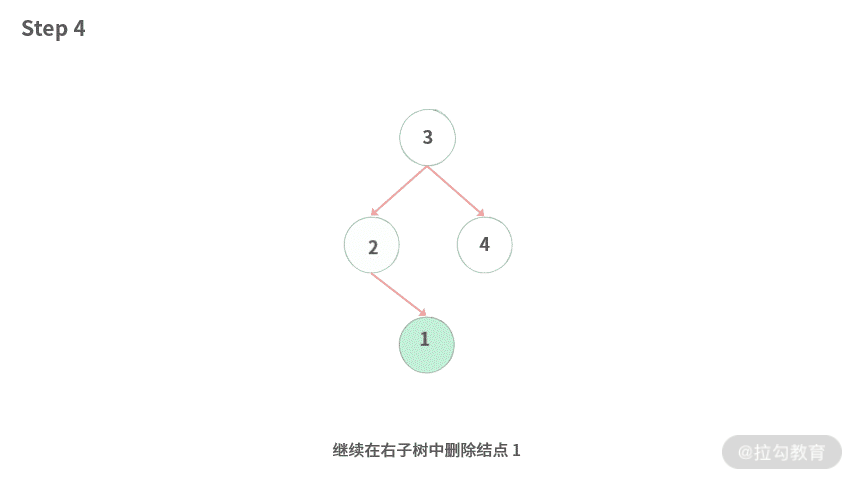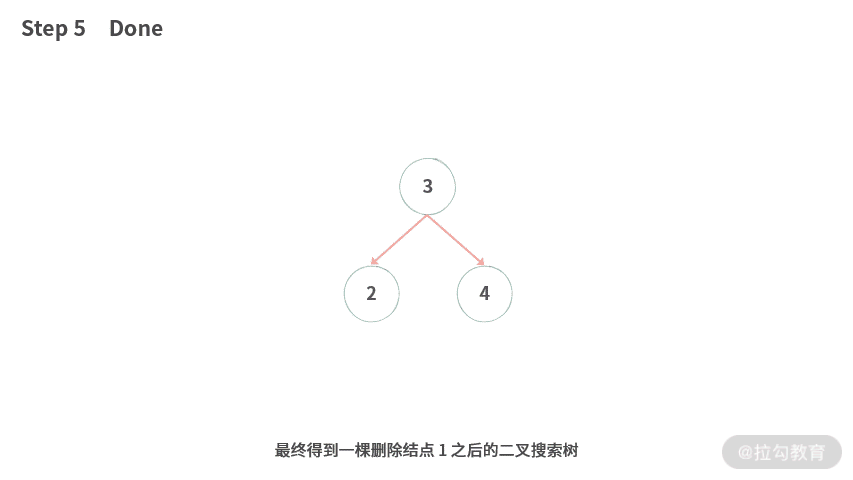
Step 1. 找到要删除的结点 1，发现它还有右子树。

Step 2. 在右子树中找到最小的值 2。

Step 3. 交换值。注意：是交换值，不是结点交换。

Step 4. 继续在右子树中删除结点 1。

Step 5. 最终我们得到一棵删除结点 1 之后的二叉搜索树。

d）被删除的结点既有左子树，也有右子树。这时，假设它只有左子树，或者假设它只有右子树，这两种假设你可以任选一个进行删除即可。

不过这里我要给你留道思考题：如果我们想要删除结点之后，想让二叉搜索树尽量保持平衡，有什么办法呢？提示：可以增加一些结点信息。

【代码】至此，我们把删除二叉搜索树的结点涉及的所有情况都分析清楚了，接下来就可以直接写代码了（解析在注释里）：

class Solution {
private void swapValue(TreeNode a, TreeNode b) {
int t = a.val;
        a.val = b.val;
        b.val = t;
    }
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
        }
if (key < root.val) {
            root.left = deleteNode(root.left, key);
        } else if (key > root.val) {
            root.right = deleteNode(root.right, key);
        } else {
if (root.left == null && root.right == null) {
return null;
            } else if (root.left != null) {
                TreeNode large = root.left;
while (large.right != null) {
                    large = large.right;
                }
                swapValue(root, large);
                root.left = deleteNode(root.left, key);
            } else if (root.right != null) {
                TreeNode small = root.right;
while (small.left != null) {
                    small = small.left;
                }
                swapValue(root, small);
                root.right = deleteNode(root.right, key);
            }
        }
return root;
    }
}

代码：Java/C++/Python

复杂度分析：如果是一棵平衡的二叉搜索树，那么时间复杂度为 O(lgn)，否则时间复杂度为 O(N)。

【小结】我们对 “二叉搜索树的删除结点” 的考点做一下小结。一方面是利用有序性，另一方面就是考察应聘者的分析能力。因此，这道题的重点是清晰分析出其中涉及的四种情况。面试的时候，面试官会要求你：

• 能清晰地讲出每种情况的处理办法
• 能清晰简洁地实现代码

既然我们已经学习了二叉搜索树删除结点操作，那么另外两种操作想必你可以拿来练练手了。

练习题 6: 二叉搜索树插入一个新结点

代码：Java/C++/Python

练习题 7：二叉搜索树查找结点

代码：Java/C++/Python

此时我们就可以将二叉搜索树的中序遍历、查找、插入，以及删除加入我们的知识树里面了，如下图所示：

后序遍历

接下来我们看一下后序遍历。后序遍历的顺序：

1. 左子树
2. 右子树
3. 根结点

这里我们同样采用一种概括处理的思路，不再按照课本上一步一步演示的方式。下图是我们处理的步骤：

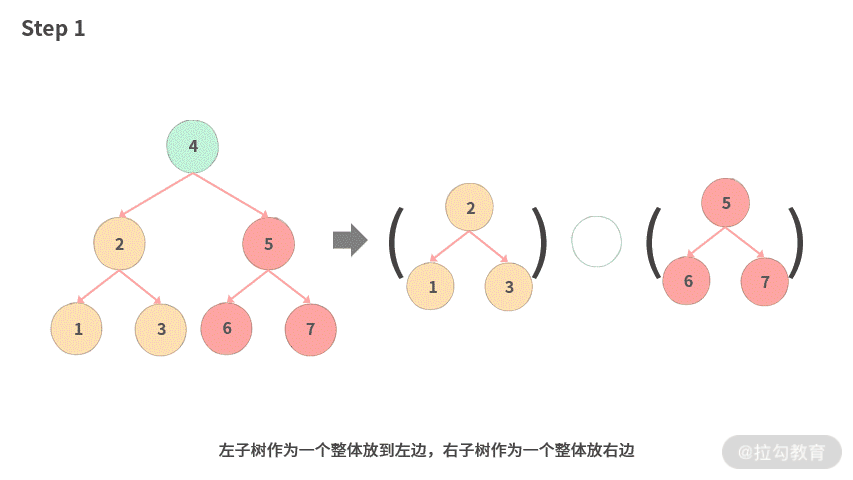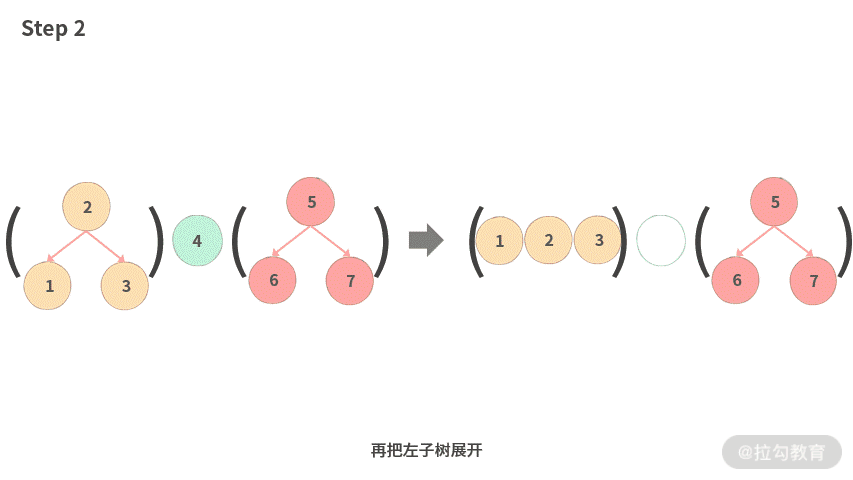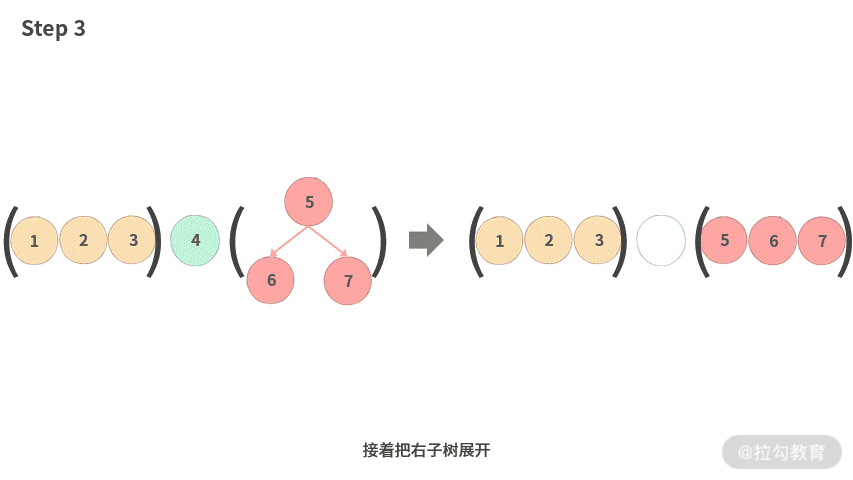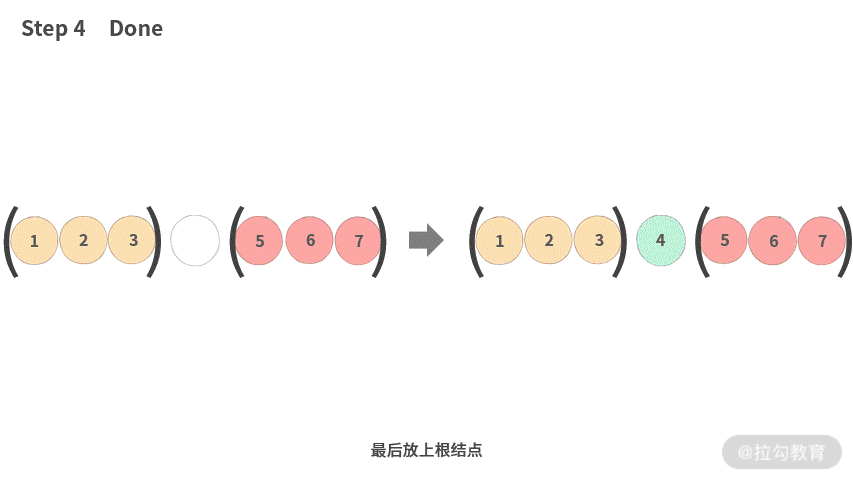
• Step 1. 左子树作为一个整体放到左边，右子树作为一个整体放右边。
• Step 2. 再把左子树展开。
• Step 3. 接着把右子树展开。
• Step 4. 最后放上根结点。

这样有助于帮助你理解后序遍历。但是仍然要注意输出结点的顺序。结点真正输出顺序如下图所示（红色表示顺序）：

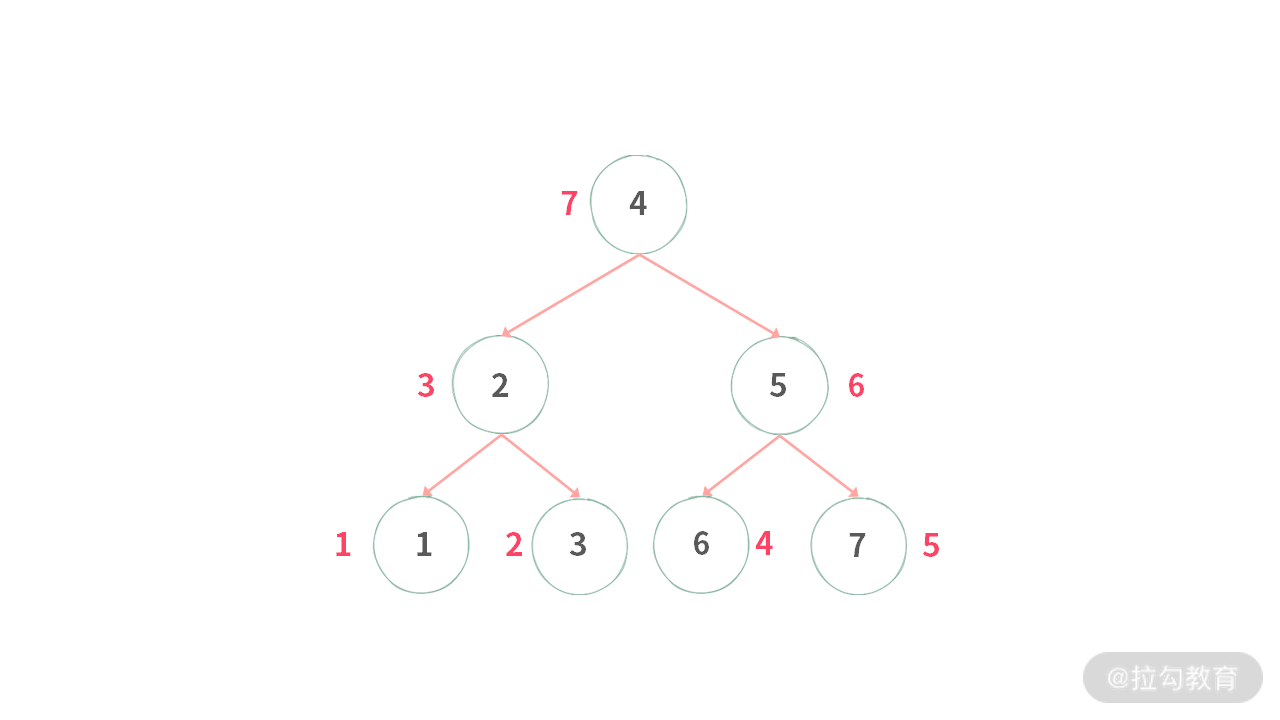
递归后序遍历

基于以上思路，我们可以写出递归的后序遍历代码（解析在注释里）：

void postOrder(TreeNode root, List<Integer> ans) {
if (root != null) {
    postOrder(root.left, ans);
    postOrder(root.right, ans);
    ans.add(root.val);
  }
}

代码：Java/C++/Python

复杂度分析：时间复杂度为 O(N)，每个结点都只遍历一次，并且每个结点访问只需要 O(1) 复杂度的时间。空间复杂度为 O(H)，其中 H 为树的高度。

使用栈完成后序遍历

接下来，我们看一下如何将递归的后序代码，改成非递归的后序代码（解析在注释里）：

class Solution {
public List<Integer> postorderTraversal(TreeNode t) {
        List<Integer> ans = new ArrayList<>();
        TreeNode pre = null;
        Stack<TreeNode> s = new Stack<>();
while (!s.isEmpty() || t != null) {
while (t != null) {
                s.push(t);
                t = t.left;
            }
            t = s.peek();
if (t.right == null || t.right == pre) {
                ans.add(t.val);
                s.pop();
                pre = t;
                t = null;
            } else {
                t = t.right;
            }
        }
return ans;
    }
}

代码：Java/C++/Python

复杂度分析：时间复杂度 O(N)，每个结点都只遍历一次，并且每个结点访问只需要 O(1) 复杂度的时间。空间复杂度为 O(H)，其中 H 为树的高度。

迭代写法的考点：判断当前结点是不是应该放到 ans 中。 这里我们用了两个条件进行判断：

• 是否有右子树
• pre 指针是不是指向当前结点的右子树

备注：虽然面试的时候极难考到 Morris，但如果你有时间我还是建议你看看 Morris 后序遍历，其优点是只需要使用 O(1) 的空间复杂度。

代码：Java/C++/Python

相比前序遍历、中序遍历，后序遍历出题形式变化更多样。接下来我们看一下如何用后序遍历处理例 1。

例 5：验证二叉搜索树

【题目】（与例 1 一样）给定一棵二叉树，要求验证是不是一棵二叉搜索树。

【分析】这里要利用后序遍历来求解这道题目。回到二叉搜索树的定义：左子树所有值都比根结点小，右子树所有值都比根结点大。

如果我们能够拿到左右子树的信息，根结点就可以利用这些信息判断是否满足二叉搜索树的要求。

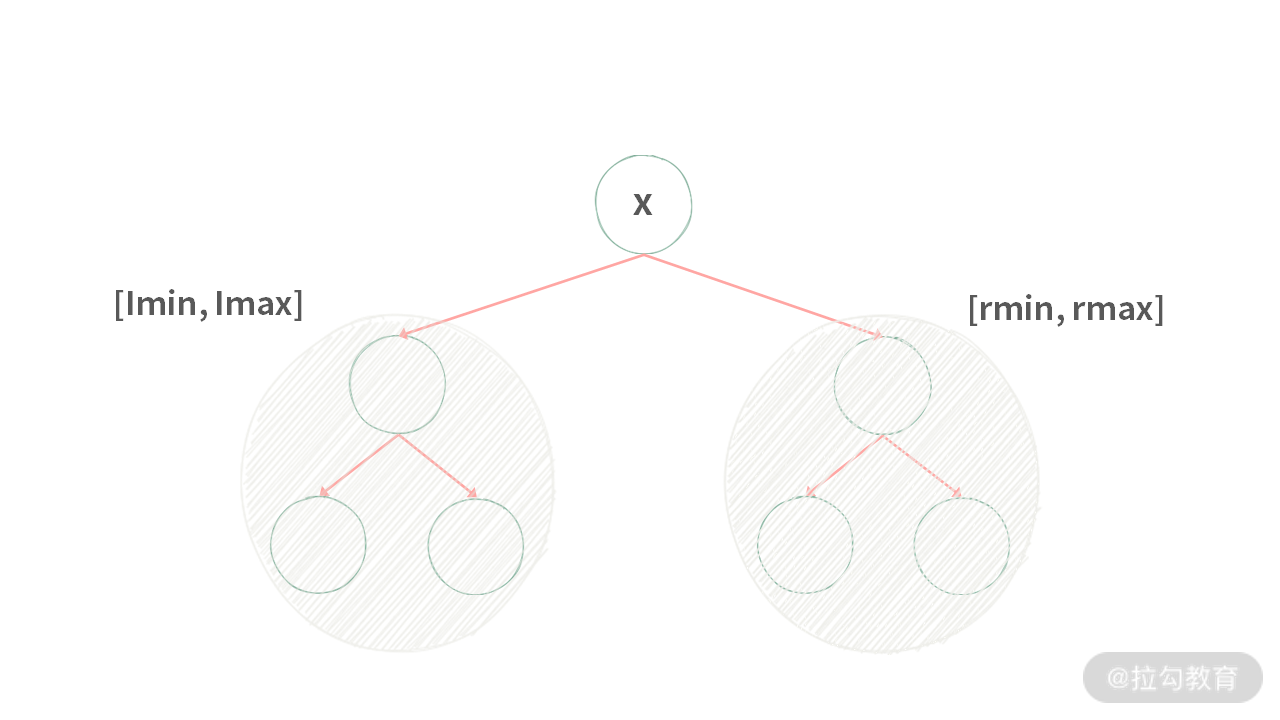
如上图所示：如果满足 lmax < x 并且 x < rmin，那么可以认为这棵树是二叉搜索树。注意，我们是先拿到了左子树与右子树的信息，然后再利用这个信息做出判断。这样的操作符合后序遍历的要求。

【画图】这里我们拿一棵二叉搜索树来画图演示步骤，动图如下：

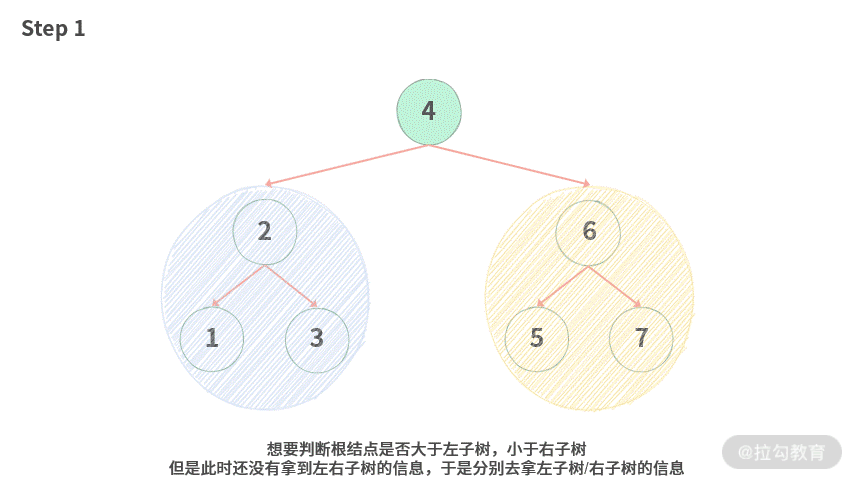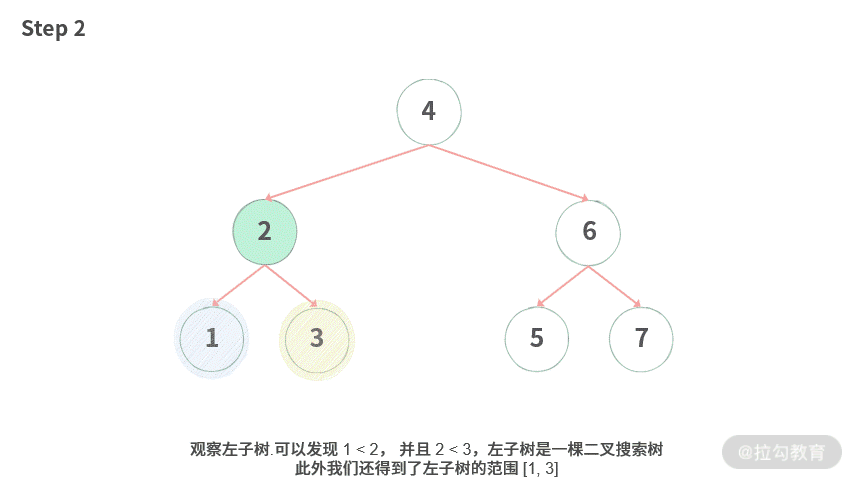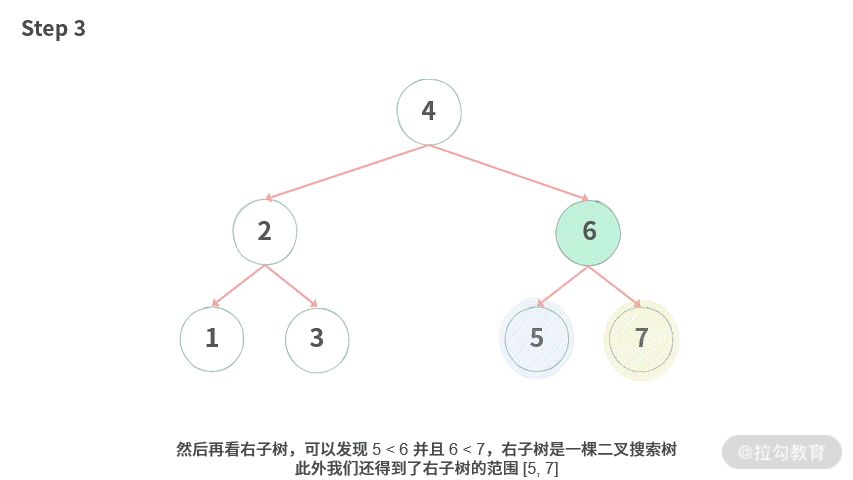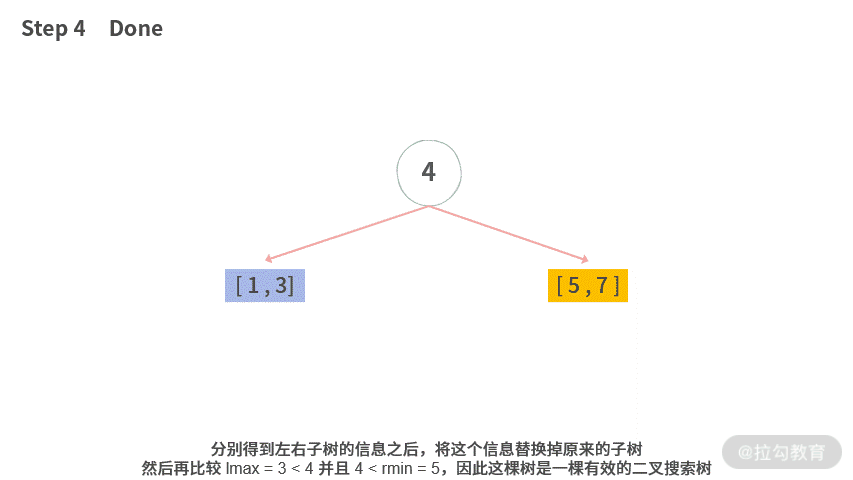
Step 1. 想要判断根结点是否大于左子树，小于右子树。但是此时还没有拿到左右子树的信息，于是分别去拿左子树 / 右子树的信息。

Step 2. 观察左子树. 可以发现 1 < 2， 并且 2 < 3，左子树是一棵二叉搜索树，此外我们还得到了左子树的范围 [1, 3]。

Step 3. 然后再看右子树，可以发现 5 < 6 并且 6 < 7，右子树是一棵二叉搜索树，此外我们还得到了右子树的范围 [5, 7]。

Step 4. 分别得到左右子树的信息之后，我们将这个信息替换掉原来的子树，然后再比较 lmax = 3 < 4 并且 4 < rmin = 5，因此这棵树是一棵有效的二叉搜索树。

【技巧】在利用后序遍历处理这道题目的时候，还需要考虑空结点带来的麻烦，如下图所示：

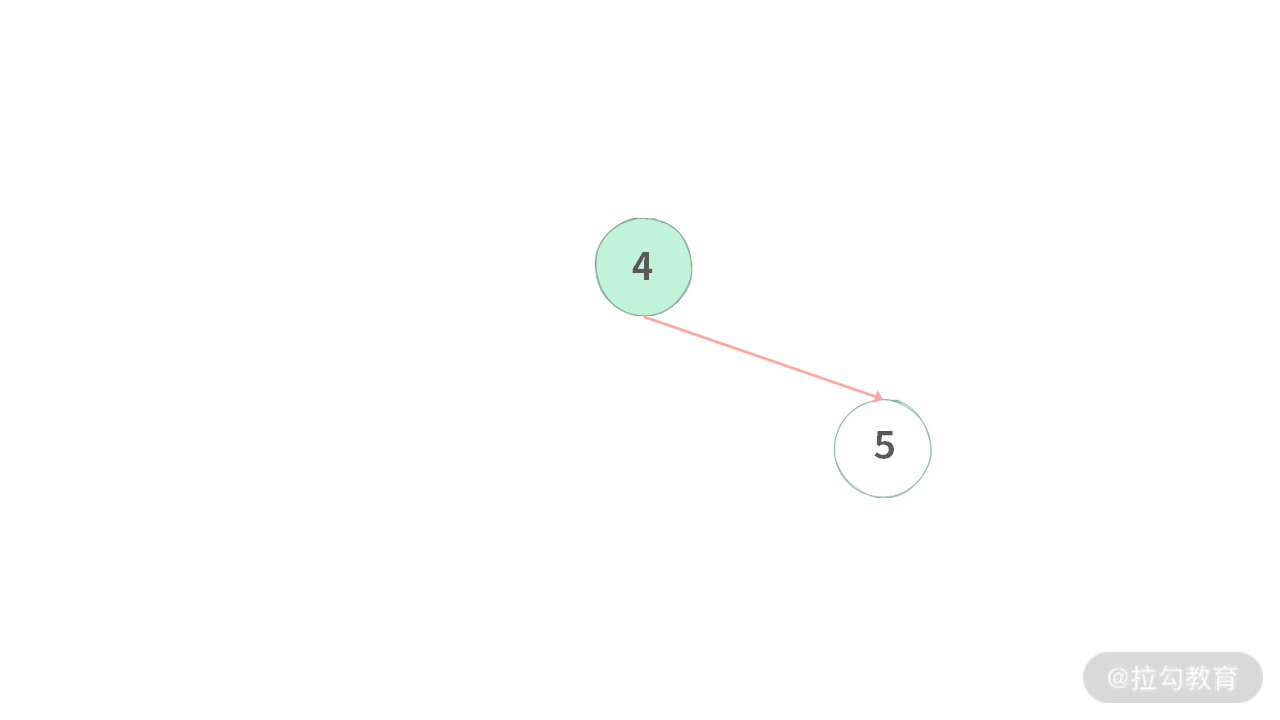
我们在处理结点 4 的时候，右子树的范围比较容易确定 [5, 5]。但是左子树是一棵空树，返回什么范围给结点 4 合适呢？有什么办法可以比较好地避免用 if/else 去判断空结点呢？

这里给你介绍一个技巧：用 [Long.MAX_VALUE, Long.MIN_VALUE] 表示一个空区间，也就是下界是一个最大的数，上界是一个最小的数。

下面我们利用动图演示一下为什么在这种情况下可以工作（画图时分别用 -inf 取代最小值，用 inf 取代最大值）：

Step 1. 根据后序遍历的要求，首先应该去查看左子树和右子树的信息。

Step 2. 左子树是一棵空树，那么得到的区间就是 [inf, -inf]。注意这里表示空区间的方式。

Step 3. 右子树只有一个结点 5，其左右子树也是空树，因此结点 5 的左右区间分别为 [inf, -inf] 和 [inf, -inf]。接下来进行比较，lmax = -inf < 5 并且 5 < rmin = inf。

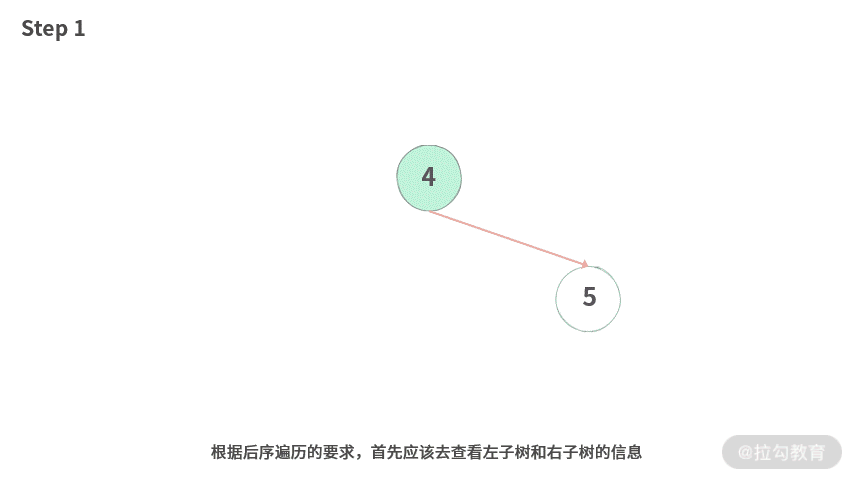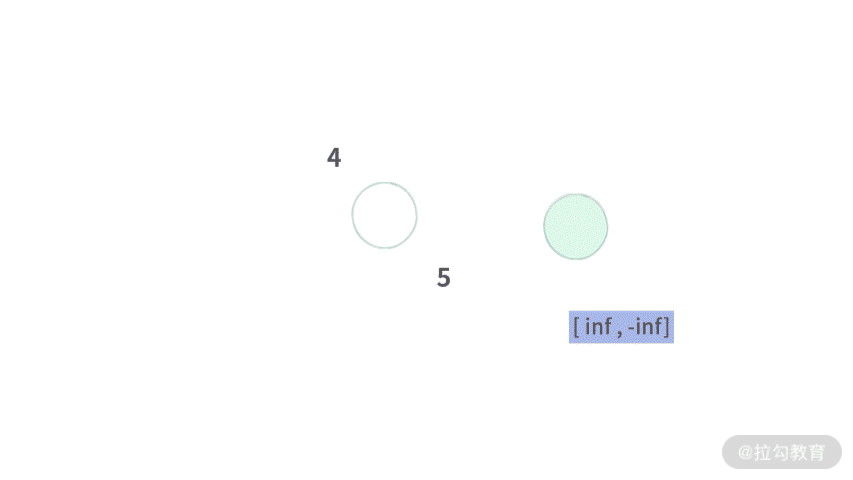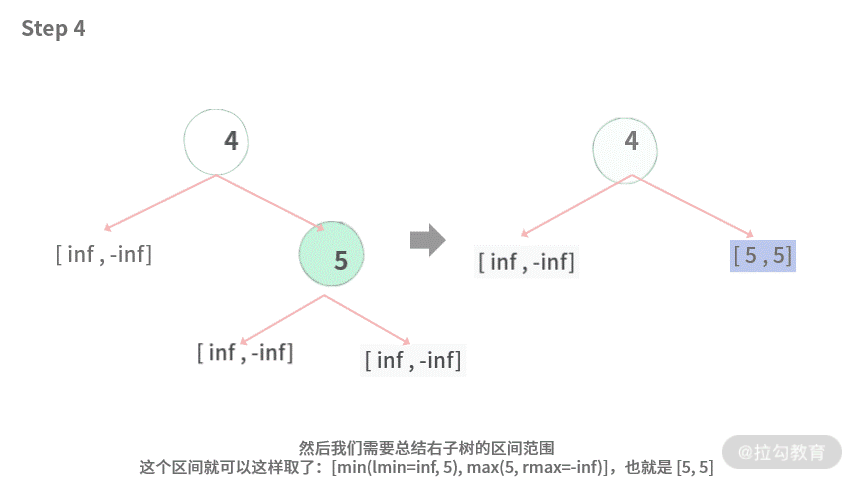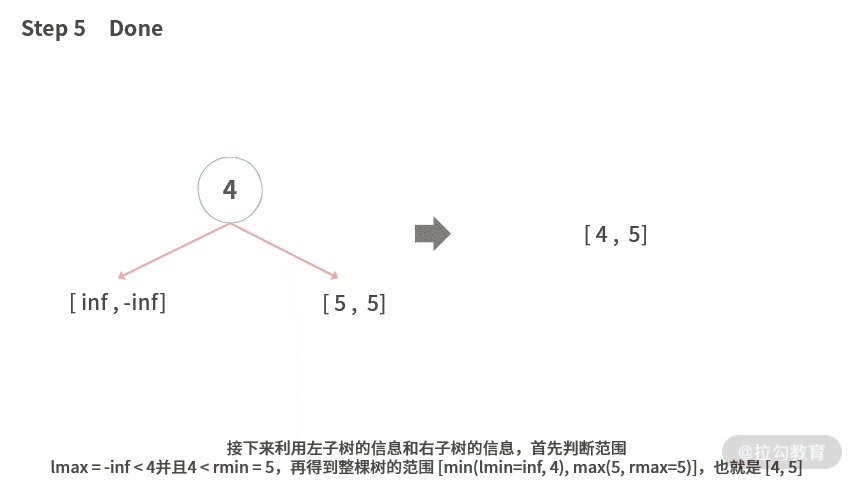
Step 4. 然后我们需要总结右子树的区间范围。这个区间就可以这样取了：[min(lmin=inf, 5),max(5, rmax=-inf)]，也就是 [5, 5]。

Step 5. 接下来利用左子树的信息和右子树的信息，首先判断范围，lmax = -inf < 4 并且 4 < rmin = 5，再得到整棵树的范围[min(lmin=inf, 4),max(5, rmax=5)]，也就是 [4, 5]。

【代码】到这里，我们已经可以开始写一下代码了（解析在注释里）：

class Solution {
class Range {
public Long min = Long.MAX_VALUE;
public Long max = Long.MIN_VALUE;
public Range() {}
public Range(Long l, Long r) {
      min = l;
      max = r;
    }
  }
private boolean ans = true;
private Range emptyRange = new Range();
private Range postOrder(TreeNode root) {
if (root == null || !ans) {
return emptyRange;
    }
    Range l = postOrder(root.left);
    Range r = postOrder(root.right);
if (!(l.max < root.val && root.val < r.min)) {
      ans = false;
return emptyRange;
    }
return new Range(Math.min(l.min, root.val),
                    Math.max(r.max, root.val));
  }
public boolean isValidBST(TreeNode root) {
    ans = true;
    postOrder(root);
return ans;
  }
}

代码：Java/C++/Python

复杂度分析：时间复杂度为 O(n)，空间复杂度为 O(H)，其中 H 表示树的高度。

【小结】写完代码之后，我们来看一下这道题的考点：

• 拿到子树的区间
• 利用子树的区间，整合出整棵树的区间
• 如何处理空结点

我们可以把这些知识点浓缩一下，方便我们以后复习，如下图所示：

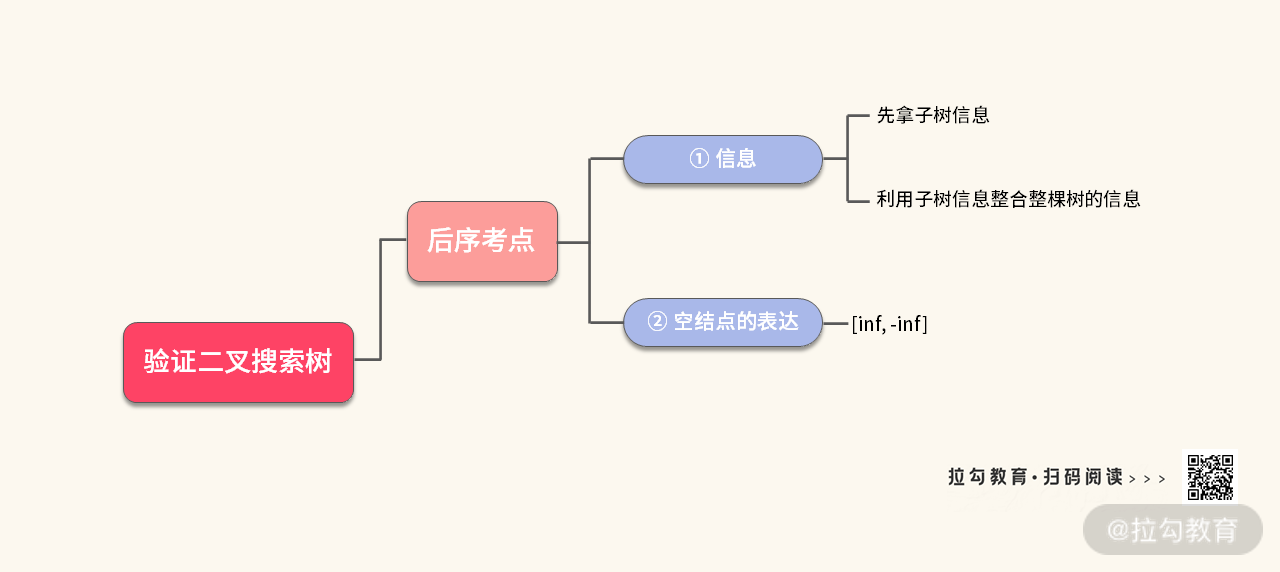
如果我们再深入思考一下，就会发现，后序遍历的时候有个特点：想要验证一棵树是否是二叉搜索树，后序遍历的返回值却是整棵树的信息。

这里画图来表示一下：

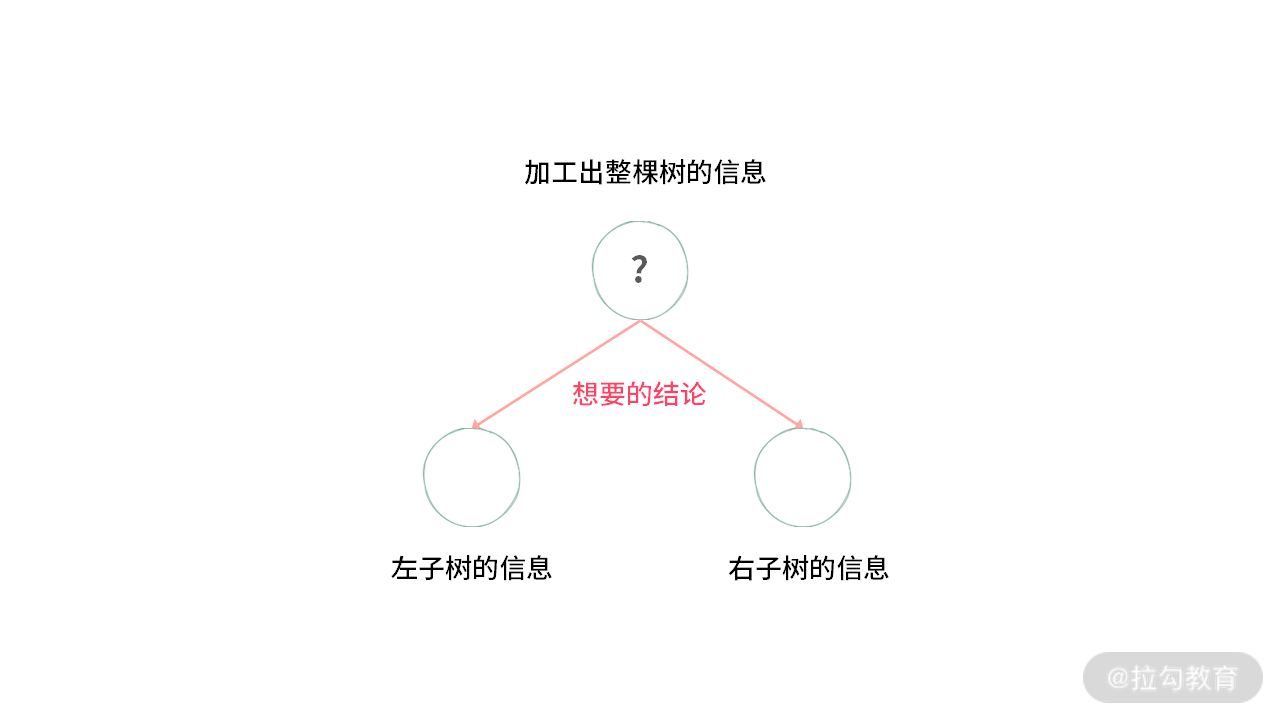
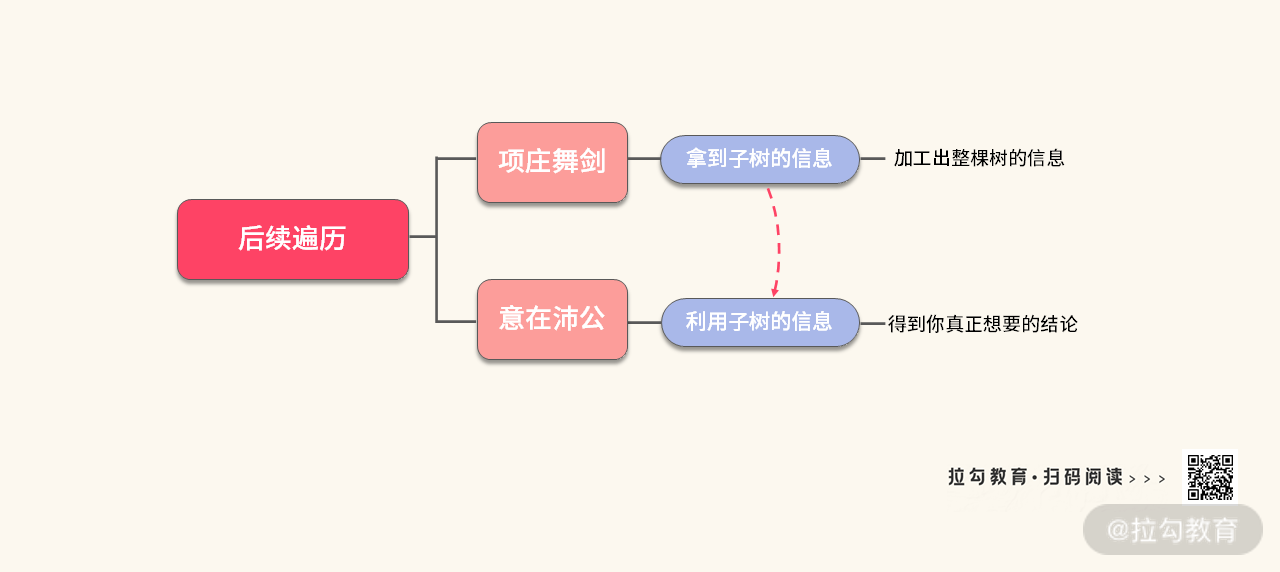
有点 “项庄舞剑，意在沛公” 的味道。那么我们再对后序遍历做一个小结，如下图所示：

完成总结后，我们再通过一道题目，加深对这个考点的理解。

例 6：最低公共祖先

【题目】给定一棵二叉树，和两个在树上的结点，返回这两个结点的最低公共祖先。比如 [5,3] 两个结点的最低公共祖先是结点 6。

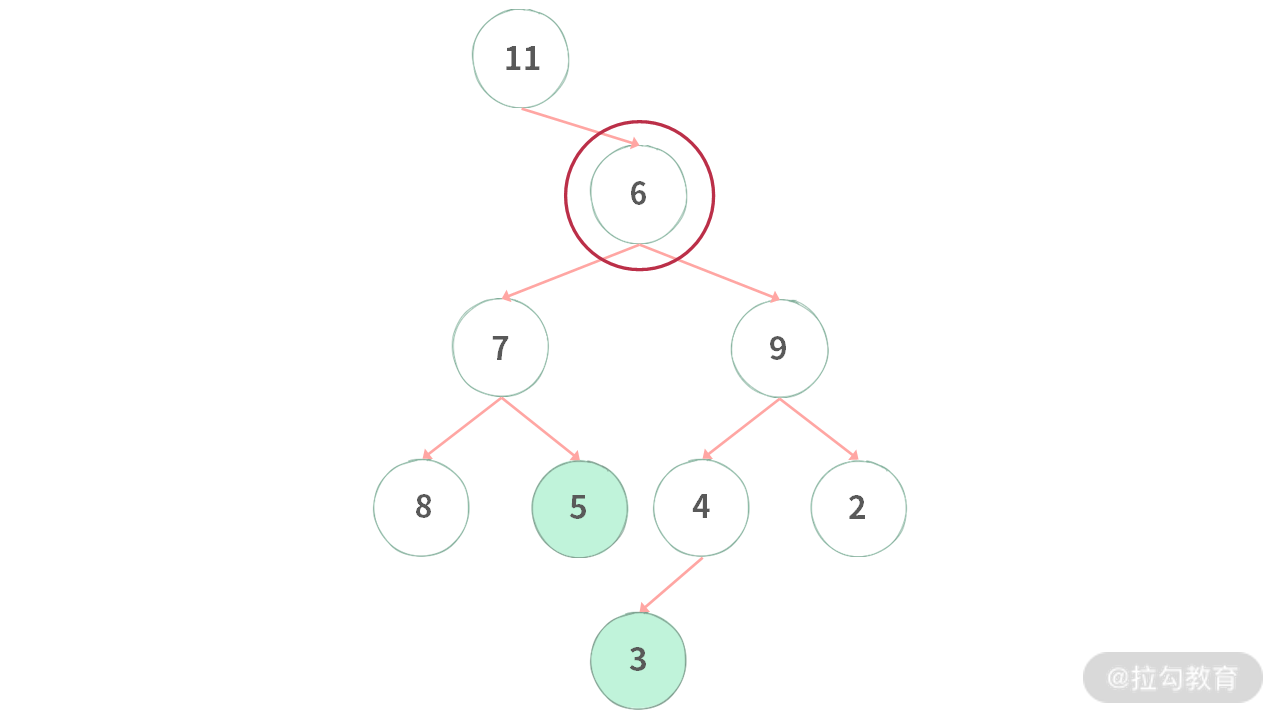
【分析】这是一道来自微软的面试题。在面试时，注意面试官要求的是两个结点的最低公共祖先。

一个结点 x 如果是 p，q 的最低公共祖先，那么以结点 x 为根的树，必然包含了 p，q 这2个结点。并且只可能下面 2 种 Case。

Case 1：两个结点 p，q 分别在 x 的左边和右边。此时左子树会找到 1 个结点，右子树会找到 1 个结点。如下图所示：

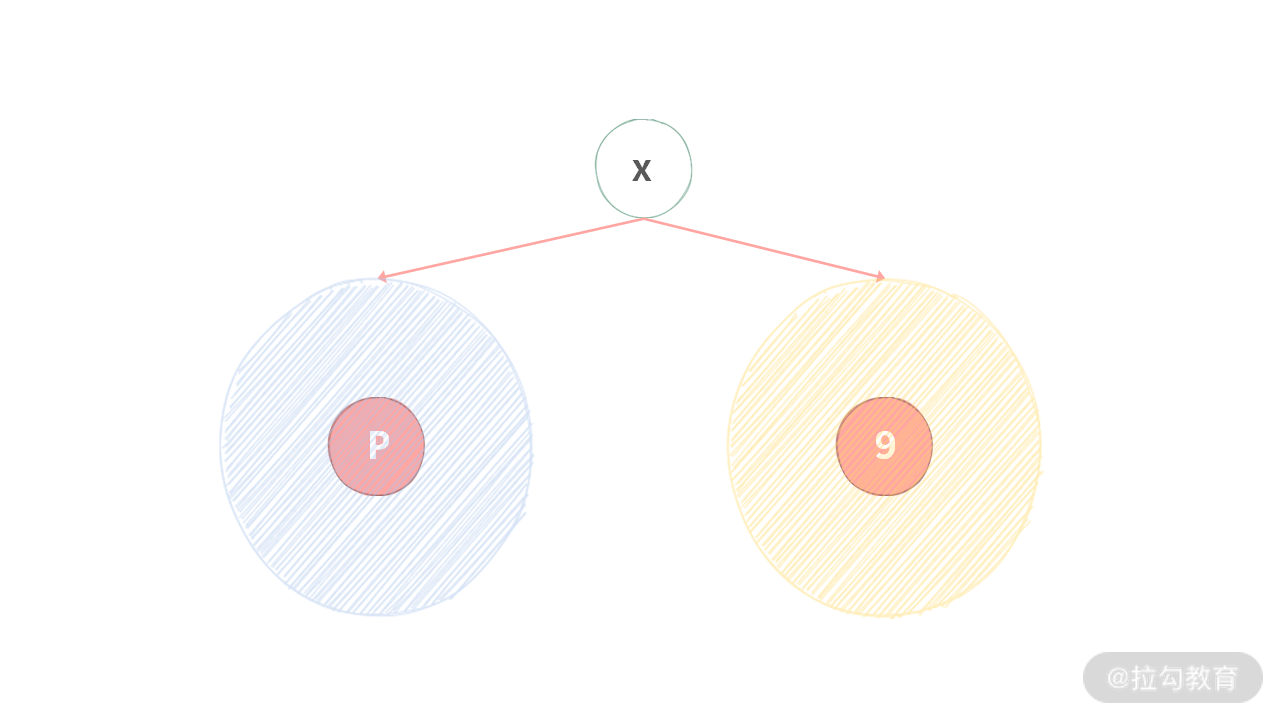
Case 2：根结点为 q，另外一个结点 p 在子树里，反之亦然。如下图所示：

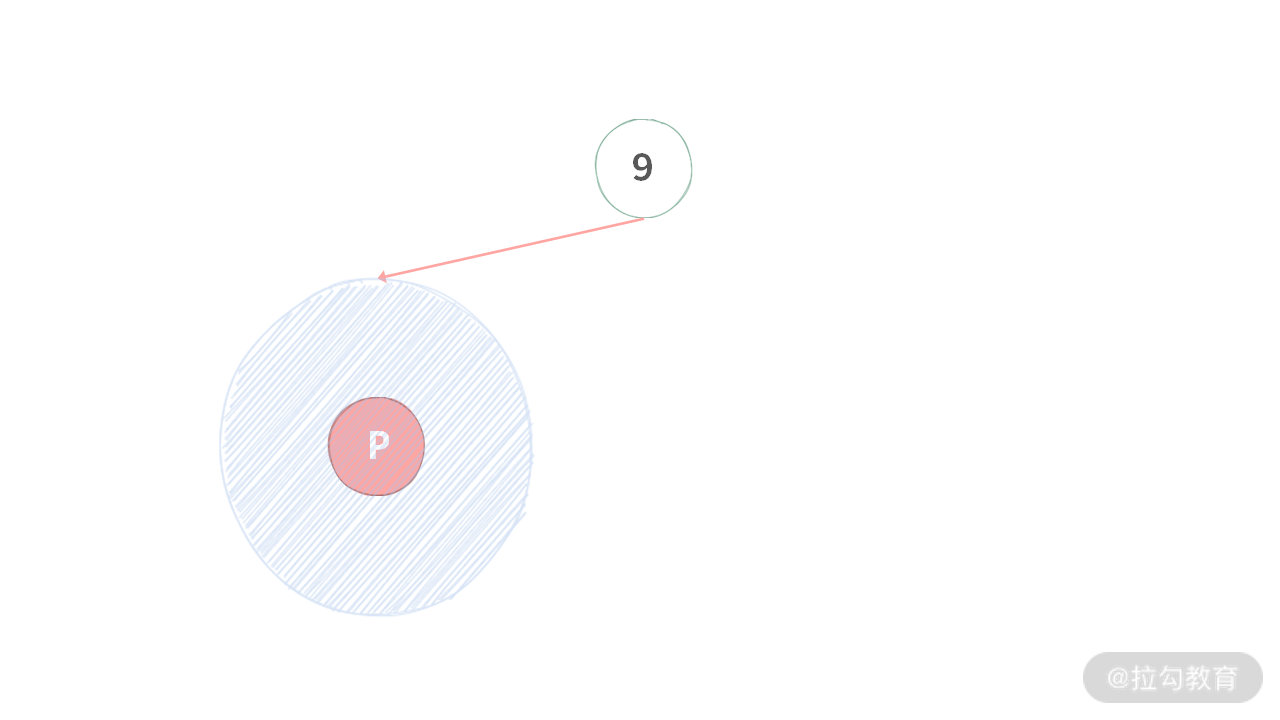
这里你可能会想，如果左子树找到 2 个结点怎么办？比如下图展示的情况：

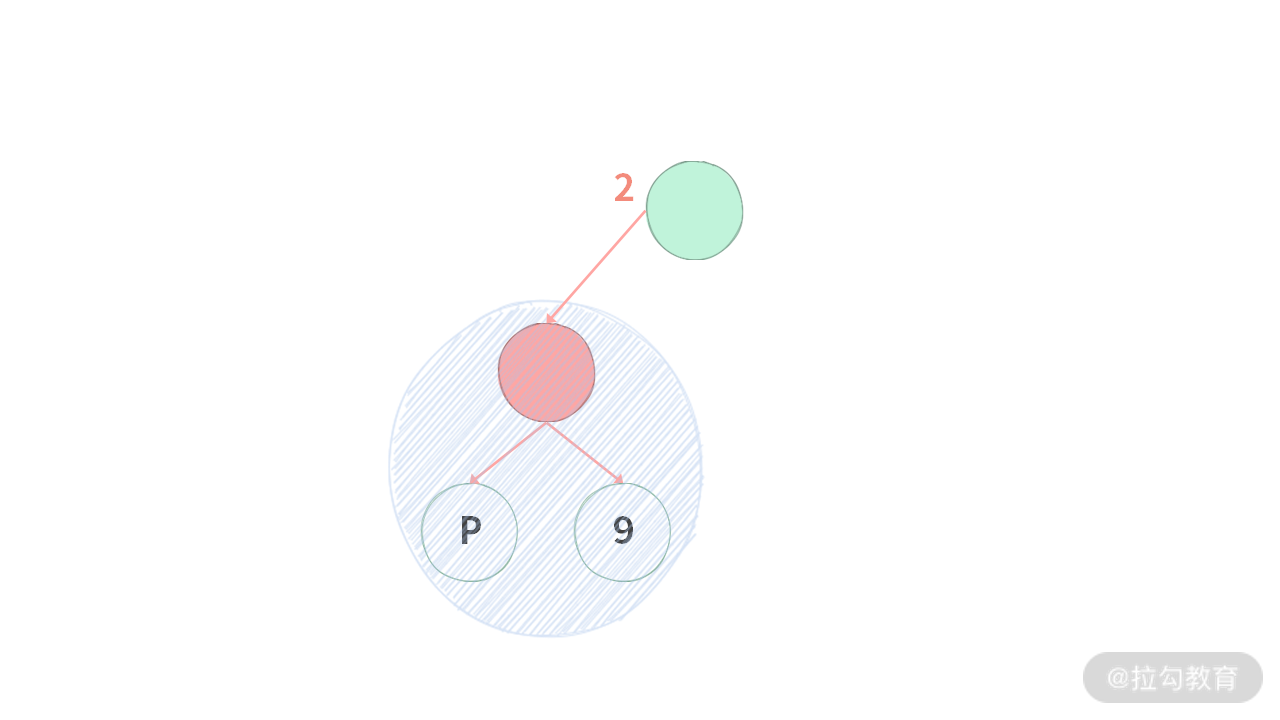
绿色结点发现左子树计数有两个结点，那么绿色结点肯定不是最低公共祖先，最低公共祖先应该是左子树，比如红色结点。说明在处理左子树时，已经找到了最低公共祖先。这种情况不需要做什么处理。

我们再提取一下分析思路里的关键信息。

• 最终想要的结论（沛公）：找到二叉树里面的最低公共祖先。
• 函数的返回值（项庄）：在当前子树中，统计结点为 p，q 的个数。

此时，我们已经有了 “沛公，项庄”，就可以展开 “鸿门宴” 了。

【画图】接下来通过一个实例先在一棵树上进行模拟，动图演示如下：

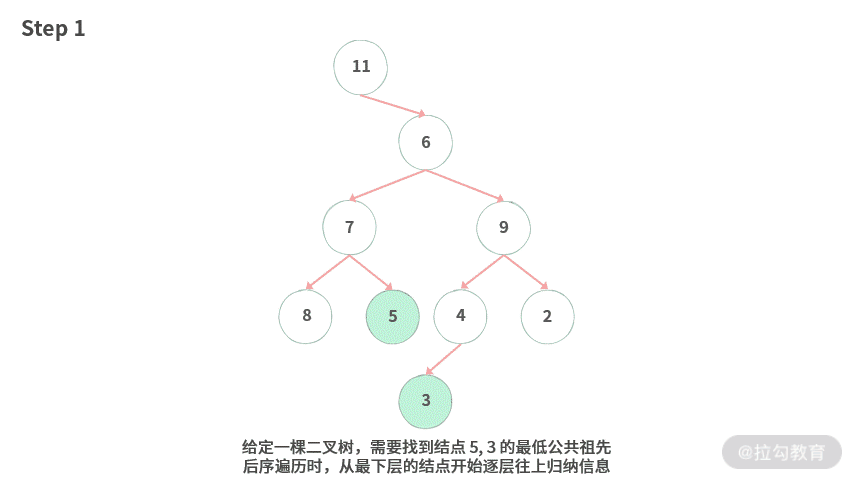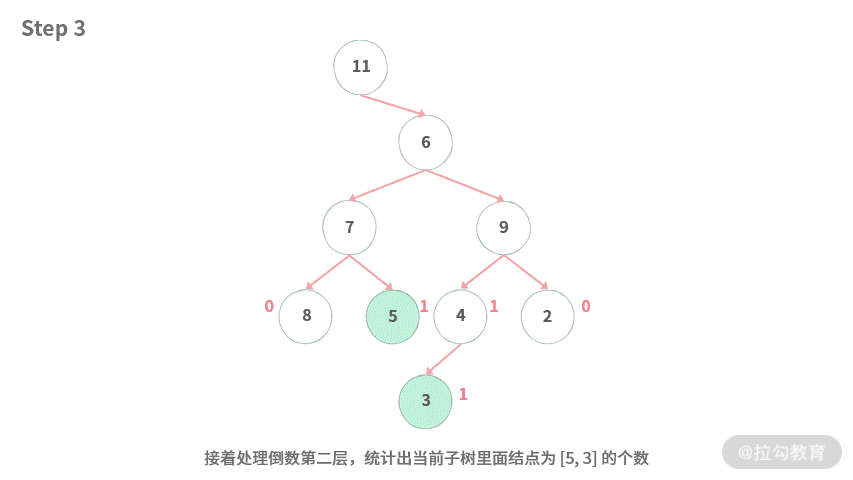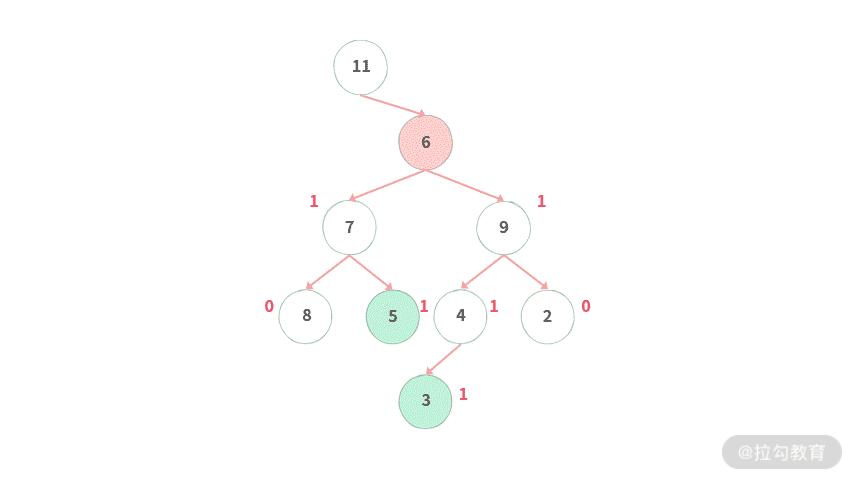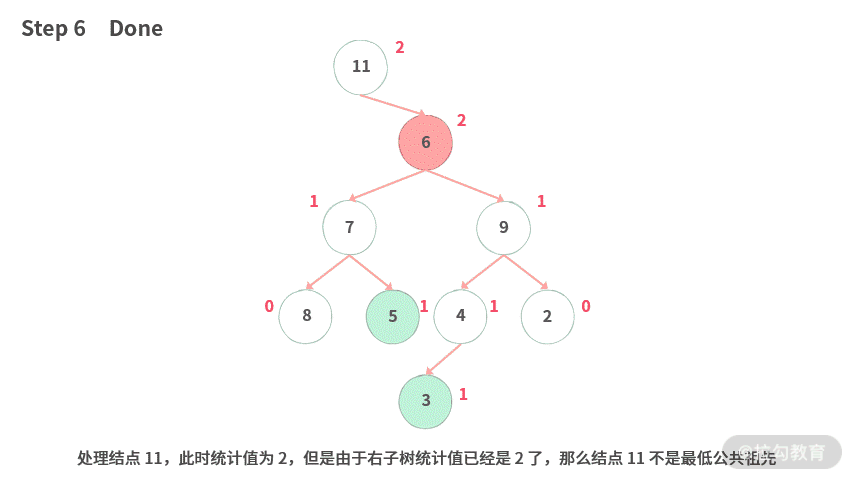
Step 1. 给定一棵二叉树，需要找到结点 5, 3 的最低公共祖先。后序遍历时，从最下层的结点开始逐层往上归纳信息。

Step 2. 最下层的结点为 3，统计数目为 1。

Step 3. 接着处理倒数第二层，统计出当前子树里面结点为 [5, 3] 的个数。

Step 4. 处理倒数第 3 层，分别统计出结点 7, 9 里面结点为 [5, 3] 的个数，[7, 9] 得到的统计值都为 1。

Step 5. 处理结点 6，此时左结点统计值为 1，右子树统计值为 1，那么最低公共祖先为结点 6。

Step 6. 处理结点 11，此时统计值为 2，但是由于右子树统计值已经是 2 了，那么结点 11 不是最低公共祖先。

【代码】至此，我们已经定义好了函数的返回值，也知道了利用子树的统计值处理前面提到的两种 Case，进而得到真正的答案。代码如下（解析在注释里）：

class Solution {
private TreeNode ans = null;
private int postOrder(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) {
return 0;
    }
int lcnt = postOrder(root.left, p, q);
int rcnt = postOrder(root.right, p, q);
if (lcnt == 1 && rcnt == 1) {
      ans = root;
    } else if (lcnt == 1 || rcnt == 1) {
if (root == p || root == q) {
        ans = root;
      }
    }
return lcnt + rcnt + ((root == p || root == q) ? 1 : 0);
  }
public TreeNode lowestCommonAncestor(TreeNode root,
                              TreeNode p, TreeNode q) {
    ans = null;
    postOrder(root, p, q);
return ans;
  }
}

代码：Java/C++/Python

复杂度分析：时间复杂度为 O(N)，空间复杂度为 O(H)，H 为树的高度。

【小结】就这道题来说，考点为：

• 定义函数的返回值为统计结点 p，q 的个数;
• 利用子树返回的结点个数，得到想要的最低公共祖先。

如果仔细思考一下，这道题还可以用前序遍历的方法来解决。你能思考一下吗？

代码：Java/C++/Python

思考题：我们再把这道题从广度和深度上进行展开：

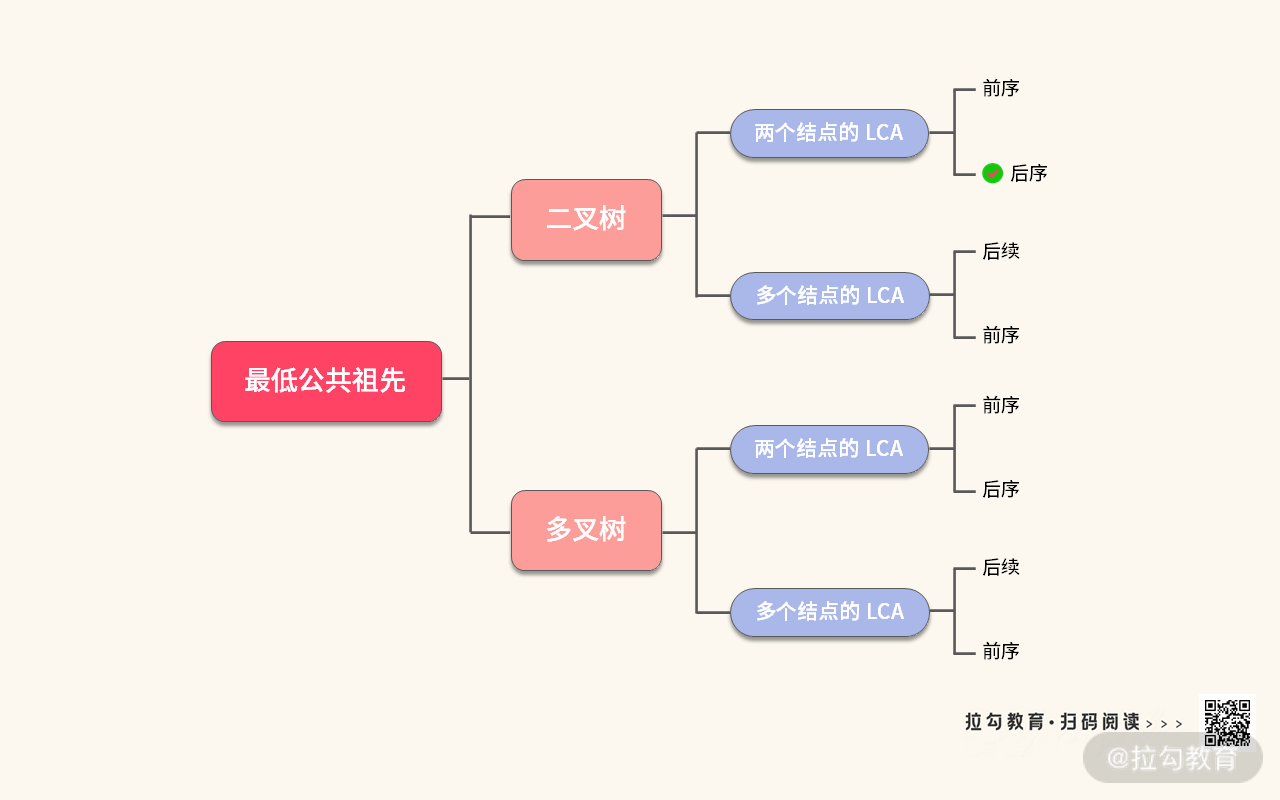
虽然我们只介绍了两个结点的后序遍历解法，但你也可以开阔思路来试一下多叉树的题目。

我们再归纳一下后序遍历的思路，可以总结为 8 个字 “项庄舞剑，意在沛公”，如下图所示：

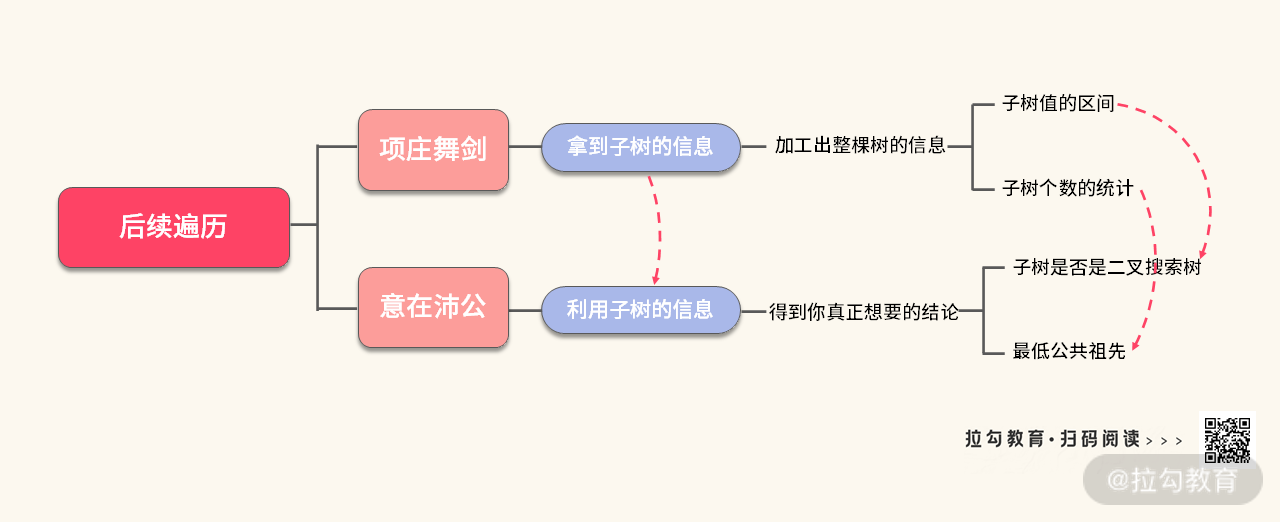
• 子树的信息：即如何定义函数的返回值。可以巧妙记为 “项庄是谁？”。
• 信息的处理：如何利用子树返回的信息，得到我们最终想要的结论，可以巧妙地记为 “如何得到沛公？”。

总结与延伸

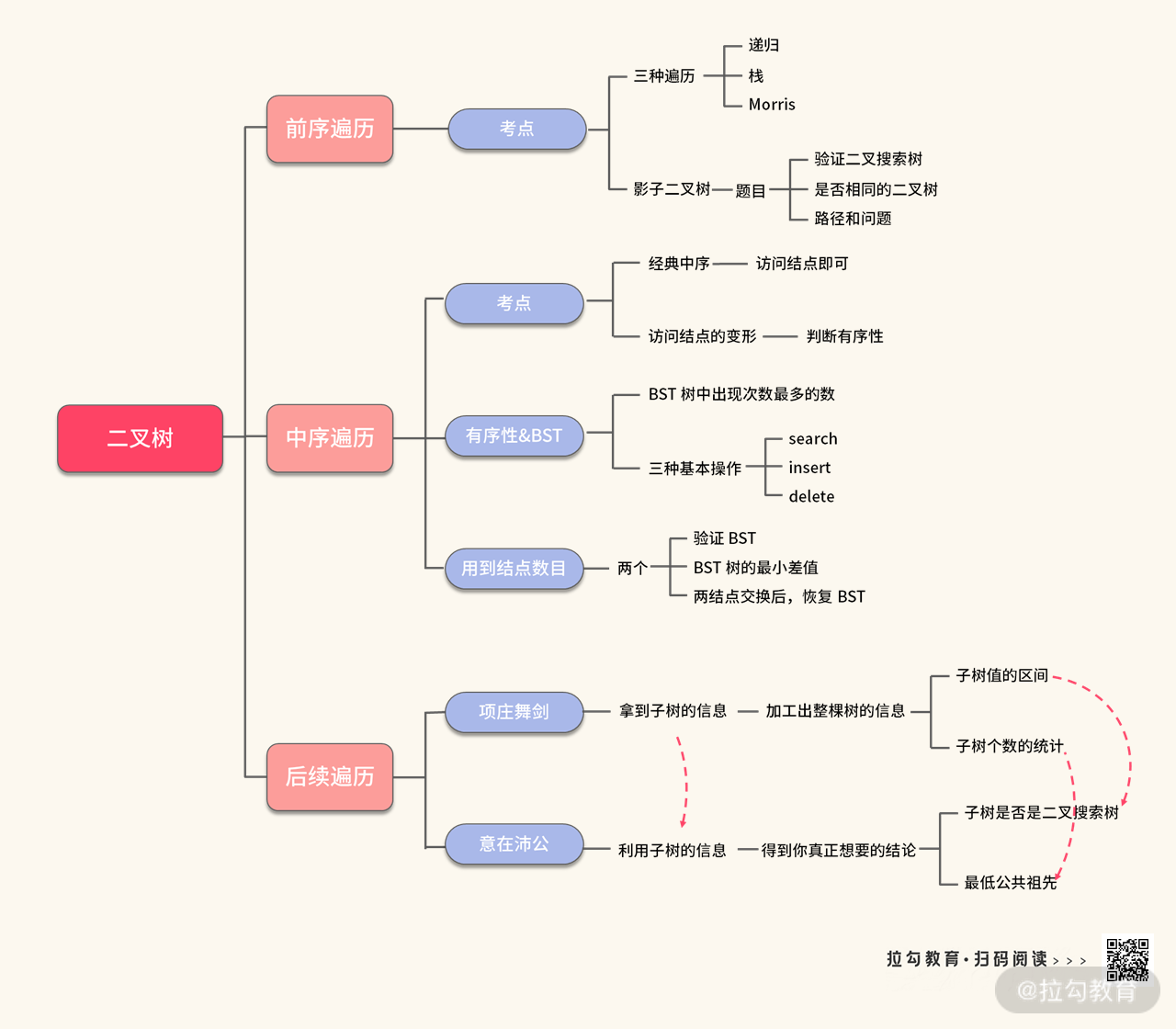
经过前面几讲的学习，我们马上就要和二叉树说再见了，回到知识层面，我再把本讲重点介绍，且需要你掌握的内容总结在一张思维导图中，如下图所示：

除去知识的扩展，你还要学会浓缩和简化，抓住三种遍历的核心。我同样为你总结了一张思维导图：

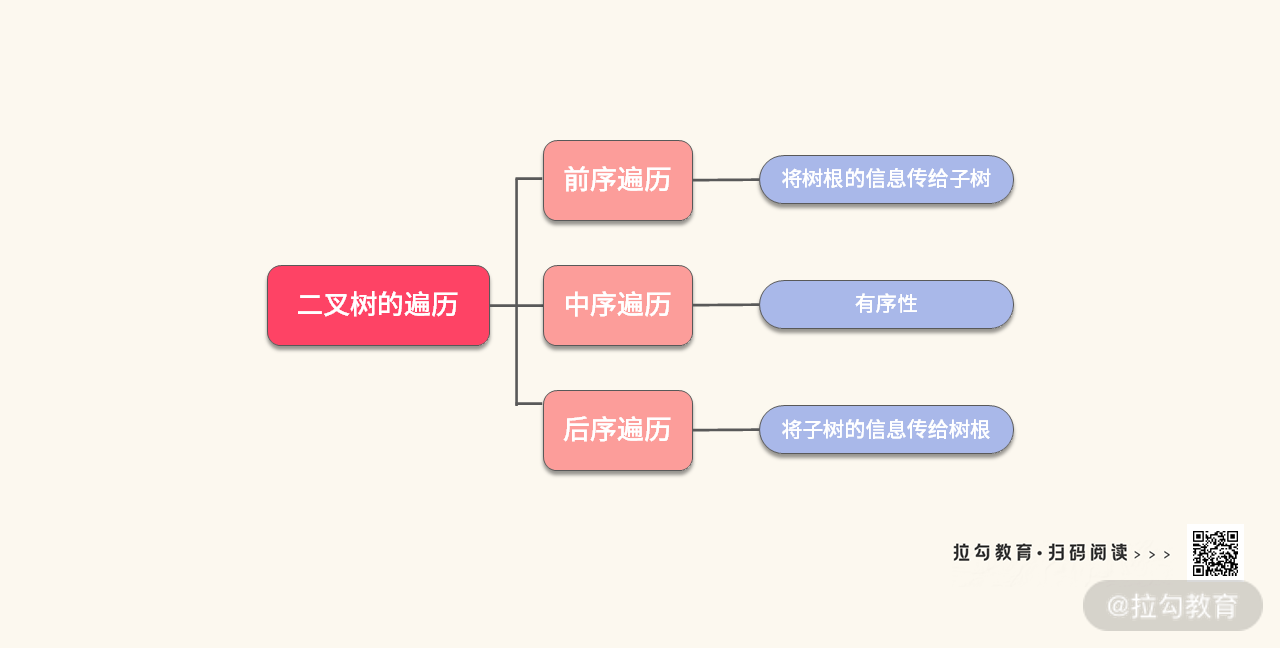
除去介绍知识本身，这里我重点介绍了 “我是如何通过三种遍历搞定所有的二叉树的题目”。由于篇幅的限制，关于 “树” 的介绍就要到这里。今天所讲的内容只是一引子，期待你还能发现更多树的特点和巧妙用法。欢迎在评论区和我交流，期待看到大家的奇思妙想。

思考题

我再给你留一道思考题：给定一个二叉树的前序遍历和中序遍历，请构建出这棵二叉树。

输入：pre = [2,1,3], mid = [1, 2, 3]

输出：返回二叉树根结点 [2]，左子结点为 1，右子结点为 3.

代码：Java/C++/Python

你可以把答案写在评论区，我们一起讨论。接下来请和我一起踏上更加奇妙的算法与数据结构的旅程。你可以把答案写在评论区，我们一起讨论。接下来请和我一起踏上更加奇妙的算法与数据结构的旅程。下一讲将介绍 07 | 并查集，如何利用两行代码完成并查集的解题技巧？让我们一起前进。