数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
二分搜索在工程中有很多的应用,比如:操作系统、MySQL 、Hadoop、Spark,查找数据的时候都会用到二分搜索。
今天我们主要介绍如何使用两个简单的二分搜索模板,搞定所有的二分题目。你将收获:
- 二分搜索的两个标准模板
- 二分搜索的提问破题法
- 二分搜索的切分法
掌握这些知识点,足够应对面试中出现的二分搜索题了。Let’s GO!
二分搜索基础
二分搜索的目的是在一个有序的数组 A 里面,找到一个给定的数。比如我们想要在下面的数组里面查找 target=3。(小写字母 l 与 1 不太容易区分,文中都用大写 L 来表示。但是在图片和代码中,仍然用小写。 )
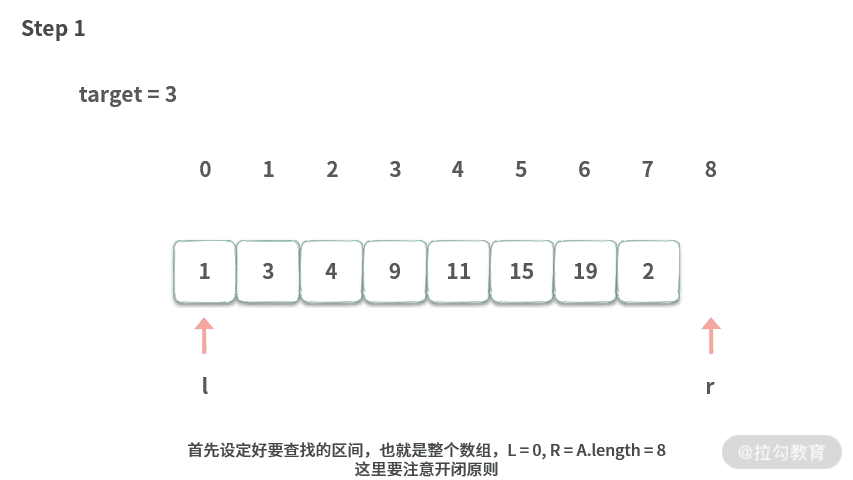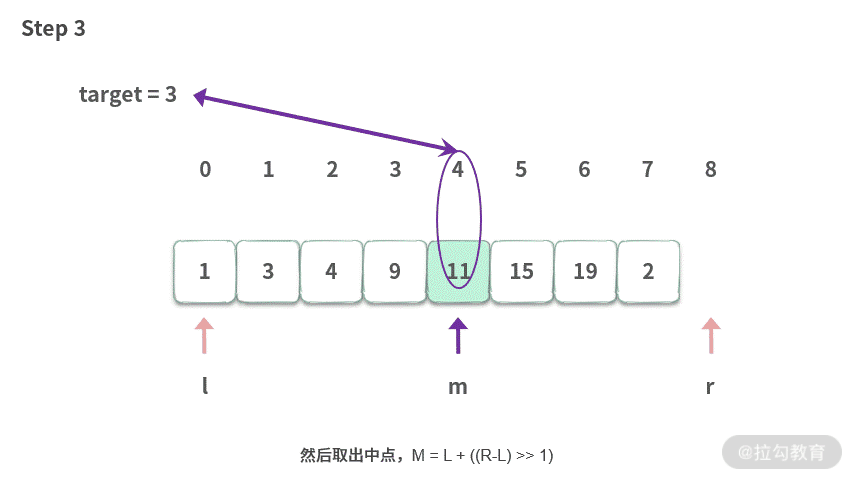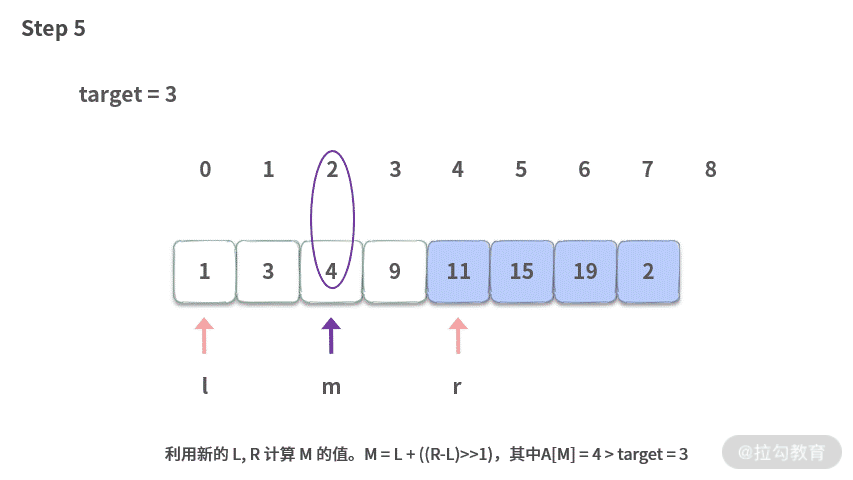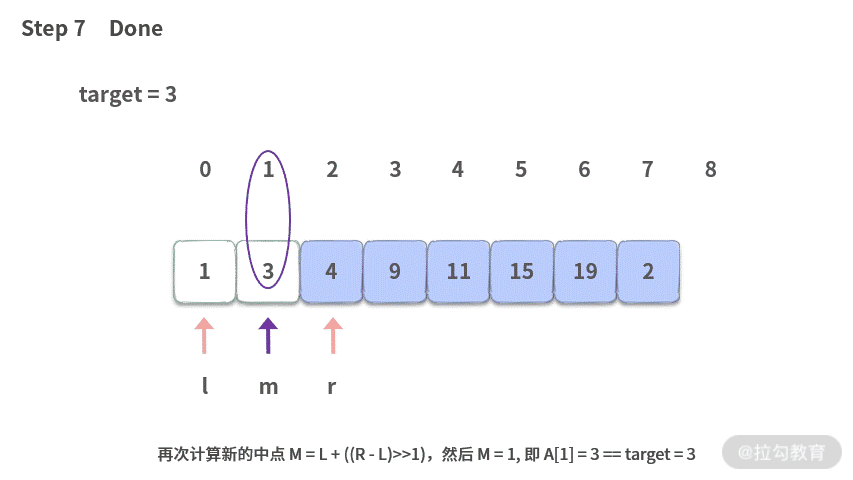
【代码】这里我们一起来复习一下这段代码(解析在注释里):
boolean binarySearch(long[] A, long target) {if (A == null || A.length == 0) {return false;}int l = 0, r = A.length;while (l < r) {final int m = l + ((r - l) >> 1);if (A[m] == target) {return true;}if (A[m] < target) {l = m + 1;} else {r = m;}}return false;}
复杂度分析:在实行二分查找时,由于每次我们都会扔掉一半的数据,所以总共只需要 O(lgn) 的时间复杂度,空间复杂度是 O(1)。
【小结】虽然二分搜索是一个非常基础的题目,但作为面试官,我看到很多候选人一不小心就栽在它上面。因此,这里我需要重点强调一下二分搜索里面的几个关键考点。
1. 开闭原则,开闭原则是一段区间的表示法。你一定要注意,写二分搜索的时候,每一个区间的表示都是严格按照开闭原则进行的。这是面试中一个非常重要的考点(敲黑板,我待过的几家公司都喜欢考察)。
2. 区间的变化,要深度理解区间的三种情况:
1)扔掉左区间为什么是 L = M + 1,扔掉右区间为什么是 R = M;
2)为什么一个 L 要加 1,一个 R 不加 1;
3)为什么循环的条件需要是 L < R。
3. 代码流畅度,这已经是一个非常非常基础的算法了,如果你在写代码的时候还会出现卡壳,那么我建议你思考以下两个问题:
1)是否真的深度理解开闭原则在二分搜索里面的体现?
2)是否真的记住这个代码模板了?
这里请你思考,或者说再联想一下,其他算法是否深度依赖开闭原则呢?
根据条件,在运行过程中,不断扔掉一半数据,然后在剩下的一半数据进行查找的算法还有哪些?这里我简单罗列了一下,如下图所示:
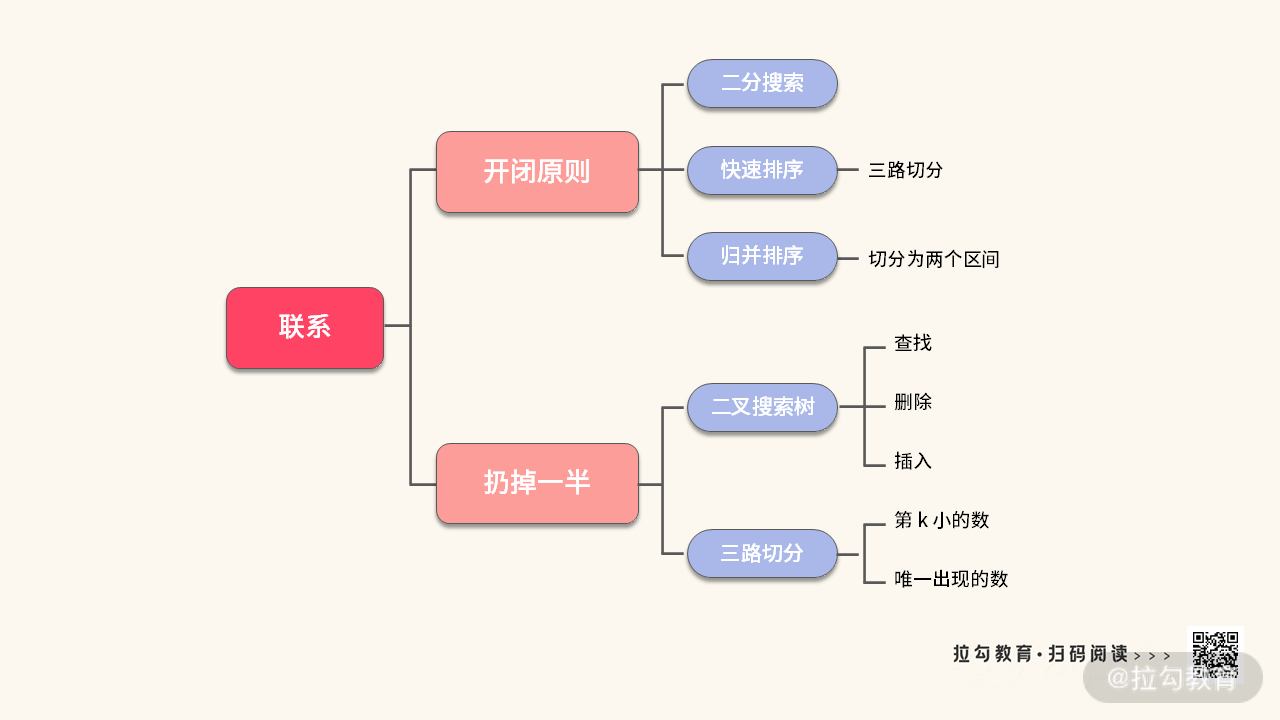
你还能做进一步的补充吗?在学习的过程中,一定要有意识地让新的知识与旧的知识产生联系。上图展示的是一种广度拓展,接下来我们来看一下深度拓展。
例 1:有序数组中最左边的元素
【题目】给定一个有序数组,返回指定元素在数组的最左边的位置
输入:A = [1, 2, 2, 2, 2, 3, 3], target = 2
输出:1
解释:第一个出现的 2 位于下标 1,是从左往右看时,第一个出现 2 的位置。
【分析】我曾经在很多公司的电面中遇到过这个题目。其实它并不难,本质上,是一个模板题,是我们解决后续问题的基础,你需要非常牢固地理解并且记忆它的代码。否则你的二分搜索就是 “沙上建塔”。
这道题目可能会存在一些变形,比如:“找到有序数组中第一个出现的 2”,或者 “找到数组中最后一个出现的 2”。
一个不正确的回答是:“先利用二分找到一个 2,然后再向左右两边搜索”。但是这么一来,时间复杂度就变成 O(N)。
那么有没有办法降低复杂度呢?这里我们一起来看一下在二分搜索的基础上,如何找到最左边的元素。我们还是先模拟一把。
1. 模拟
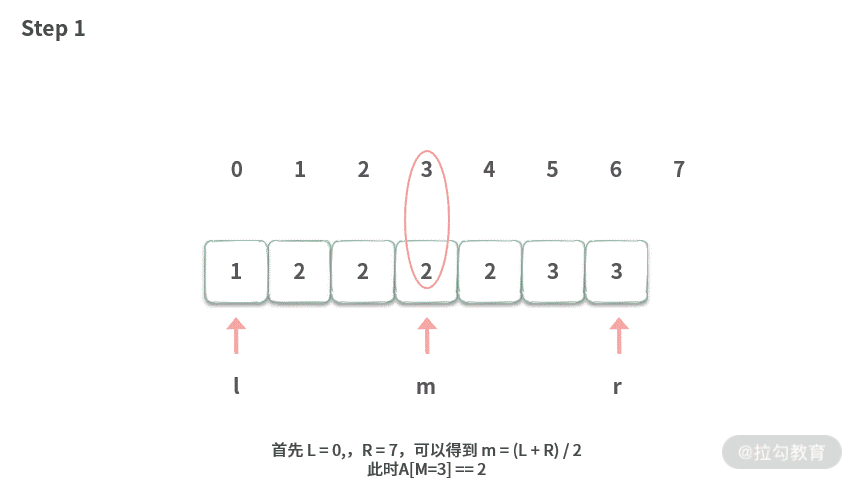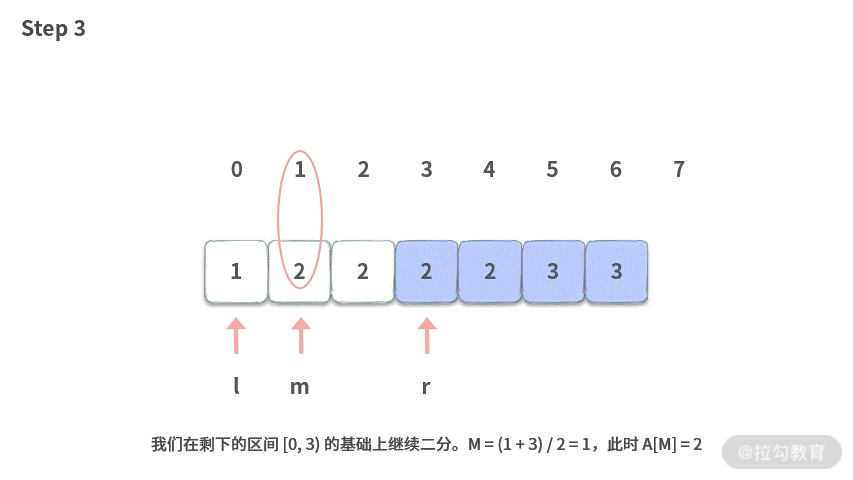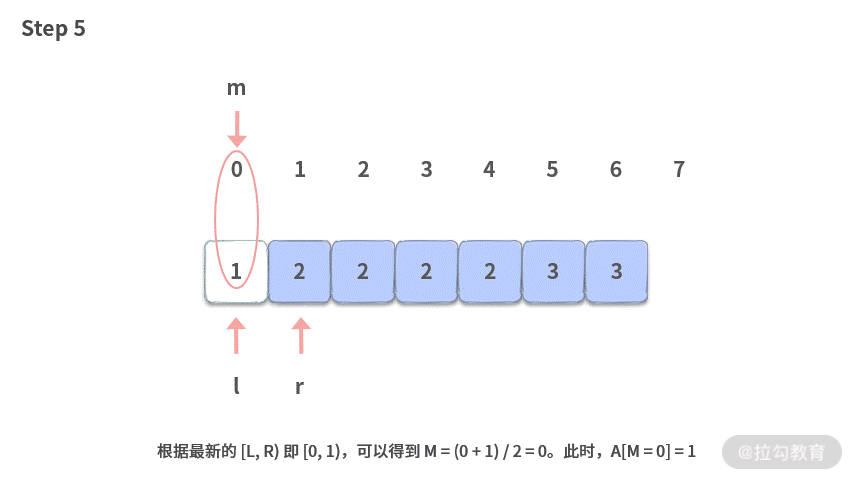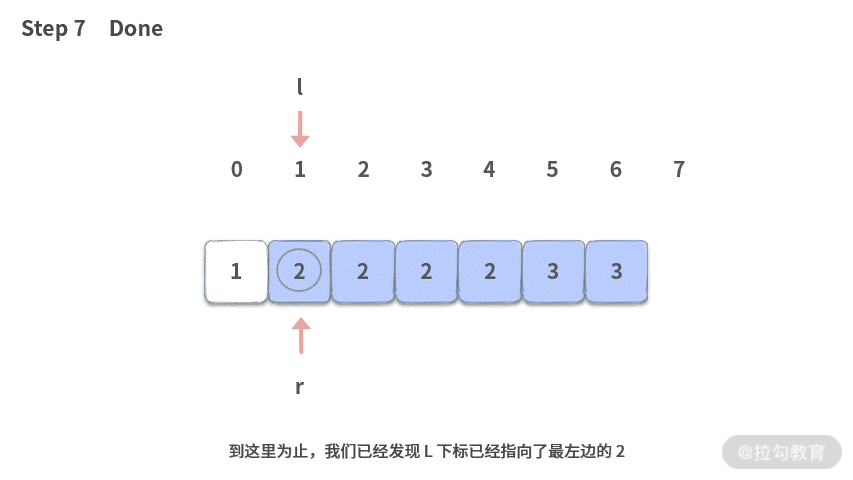
2. 规律
我们看一下上面模拟的目的已经变为:找到一个最终切分点 L,需要满足 [0, L) 区间里面的元素都必须小于 target,而 [L, ~) 右边的元素都 >= target。左边界操作原则如下:
- 查找的区间一直是一个左开右闭区间 [L, R);
- 每次总是把 >= target 的区间扔掉,大于等于的不要了,然后设置 R = M;
- 当最后的区间元素都小于 target 的时候,移动 L,小于的也不要了,然后设置 L = M + 1。
可以总结为 “这也不要,那也不要”。
那么当程序最终执行结束的时候,L 必然处于以下情况之一。
- 如果有序数组中存在 target,那么必然找到最左边的 target 的位置。也就是我们模拟的情况,找到最左边的第一个 2。
- 如果有序数组中不存在 target,那么:
1)当数组中的元素都比 target 小时,L 指向数组的长度,此时访问 A[L] 非法;
2)否则,A[L] 必然 > target。
可以总结为 “要么越界,要么大于等于 target”。
3. 匹配
如果仔细一点,可以发现,这里我们在二分的时候,与传统的二分搜索相比,只是去掉了如下这个条件,最终就可以让 L 指到正确的位置。
if (A[m] == target) {return true;}
4. 边界
实际上还有几种边界情况需要讨论:
- 空数组,或长度为 0 的数组;
- 数组中的元素都小于 target;
- 数组中的元素都大于 target;
- 数组中的元素有大有小,但是 target 不存在里面;
- 数组中的元素只有一个 target。
以上这些边界都很重要,由于篇幅的原因,这里我不再详细展开。你可以自己找到一些例子来试一下 “左边界操作原则”。
面试官的建议:真实的面试中,很多人写的二分搜索的代码,经常卡在上面这几种边界上。因此,在面试中写完代码之后,主动写上测试用例是一个加分项。
【代码】模板代码如下:
int lowerBound(long[] A, int n, long target) {int l = 0, r = n;while (l < r) {final int m = l + ((r - l) >> 1);if (A[m] < target) {l = m + 1;} else {r = m;}}return l;}
复杂度分析:我们总是利用二分搜索一直进行下去,直接找到目标解。因此,算法的时间复杂度为 O(lgn),空间复杂度为 O(1)。
【小结】代码虽然短,但是我在面试候选人的时候,发现大家很容易写错这块代码。下面我给你总结一下面试时的考点。
面试考察点:
- 循环什么时候终止?(对应代码第 3 行)
- 什么情况下更新左边界?如何更新的?(对应代码第 5~6 行)
- 什么情况下更新右边界?如何更新的?(对应代码第 7~8 行)
所有这些问题的本质,都可以归结到一个知识点:开闭原则。
变形与延伸:
如果我们有了 lowerBound 函数,就可以利用 lowerBound 函数来写新的 binarySearch 算法了。
boolean binarySearch(long[] A, int n, long target) {int l = lowerBound(A, n, target);return l < n && A[l] == target;}
实际上,在 C++ 的 STL 库里面的 binary_search 函数就是通过这种方式实现的。
接下来我们看第二个模板 upperBound,它的要求是:写一个函数 upperBound 寻找数组中给定元素的上界。注意,上界是刚好比 target 大的那个元素的位置。比如 A = [1, 1, 100, 100],target = 1,那么 upperBound 应该返回下标 2。
upperBound 函数是找一个切分点 y,使得:
- 所有 [0, y) 左区间里面的元素 <= target
- target < 所有 [y, ~) 右区间里面的元素
根据 upperBound 的目标,我们需要调整一下二分的策略:
- 当 A[M] <= target 的时候,需要把 [L, M] 区间扔掉。此时需要设置 L = M + 1;
- 当 A[M] > target 的时候,需要把 (M, R) 区间扔掉。此时需要设置 R = M。
那么我们可以写出模板代码如下:
int upperBound(long[] A, int n, long target) {int l = 0, r = n;while (l < r) {final int m = l + ((r - l) >> 1);if (A[m] <= target) {l = m + 1;} else {r = m;}}return l;}
到现在为止,我们已经收获了两个模板代码:
- lowerBound,可以用来顺便解决掉 binarySearch;
- upperBound。
重要:在准备面试前,一定要理解并且熟记这两个模板代码。有个小技巧,其实 lowerBound 与 upperBound 代码是完全一样的。唯一不一样的是 A[m] 与 target 比较的时候:
- lowerBound 是 A[m] < target
- upperBound 是 A[m] <= target
如果熟练地掌握了这两个模板,那么已经有一些题目就可以轻松解决了,这里我给你留了 2 道练习题,帮你巩固下这个知识点。
练习题 1:给定一个有序数组和一个数 target,请返回起始位置和终止位置。
练习题 2:给定一个有序数组,如果要将一个数 target,插入到数组中,结果仍然有序。返回插入位置。
这里我们就这两个模板做个简单的小结:
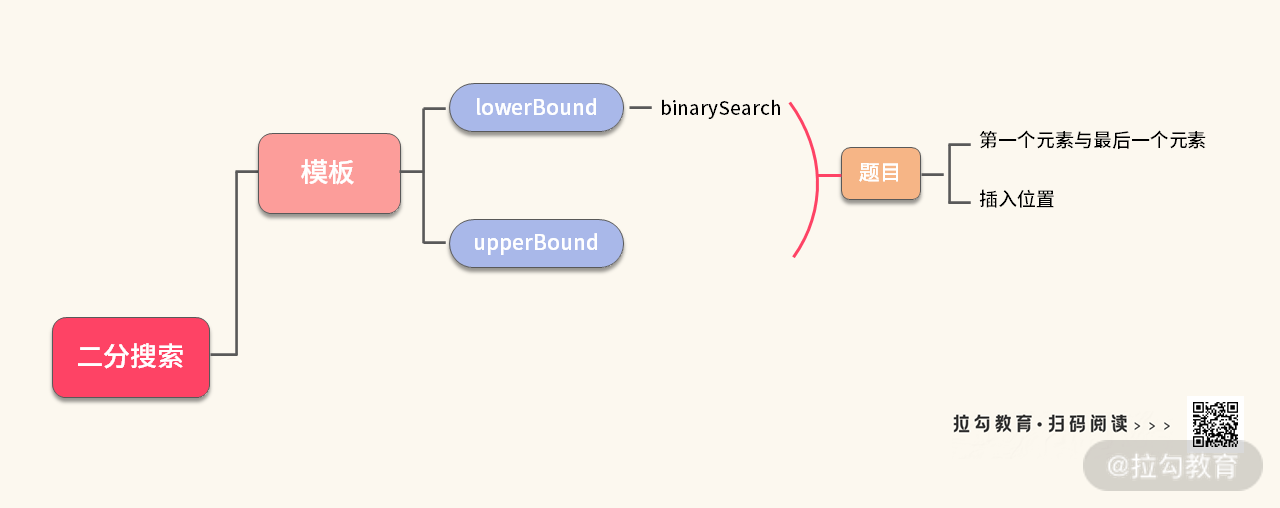
接下来我们看一下一些藏得比较 “深”,但是可以用二分搜索来破解的题。
提问破题法
到这里我们已经学习了两个二分的模板,一个 lowerBound,一个 upperBound。如果将前面学过的二分搜索进行更高层次的抽象,可以发现,利用二分搜索需要2 个条件:
- 确定搜索空间
- 搜索空间里面的值有序
这里我们引入两个符号:x 和 f(x)(放心,我们不会讲太多数学的)。
- x 表示搜索空间
- f(x) 表示通过 x 得到的值
对于最原始版本的二分搜索来说:
- x 就是下标 i,范围为 [0, N),其中 N 表示数组的长度;
- f(x) 就是 A[i]。
不过,有的面试题给的数组 A[] 并不是有序的,此时需要寻找新的 x 和 f(x) 来破题。
那么如何找到 x 和 f(x)?这里就一句话:提问就是关键。是时候拿出二分搜索比较通用的提问破题法了,不过这个方法需要通过例题才能学会,让我们一起看例题。
例 2:寻找山峰
【题目】数组里的元素组成一个山峰,位于峰顶的元素,总是比它左边和右边的元素大。请把这个下标找出来。
输入:A = [1, 2, 3, 2, 1]
输出:2
解释:我们发现 A[2] = 3 大于左边和右边的所有元素,并且数组刚好是个山峰。
【分析】前面我们说过击破二分搜索题的关键就是看提问。提问破题法的第一步:要什么,什么就是 x。
找到下标,满足比左边和右边的元素都大
问题要的是 “数组的下标”,所以我们可以确定:x 就是数组的下标。范围就是 [1, N-1),其中 N 表示数组的长度。
注意这道题的要求,因为最优解的左边有元素,所以最小下标必然为 1。而最优解的右边也有元素,所以最大下标值为 N-2。那么范围用开闭原则表示,就应该是 [1, N-1)。此时我们已经可以写出一点草稿代码了:
int l = 1, r = N-1;while (l < r) {final int m = l + ((r-l)>>1);final int mov = f(m);}
那么我们再看一下如何确定 f(x)。提问破题法的第二步:满足约束条件的 f(x)=0。

这就得出 f(x) 表示的含义:当给定一个下标 x,如果 A[x - 1]
int f(int m) {if (A[m-1] < A[m] && A[m] < A[m+1]) return 0;}int l = 1, r = N-1;while (l < r) {final int m = l + ((r-l)>>1);final int mov = f(m);}
接下来我们看一下不满足要求的 f(x)。这里需要用提问破题法的第三步:不满足约束条件的 f(x) 设置为 -1 或者 1。那么到底是设置为 -1,还是 1 呢?这个时候需要回到题目的场景中。
由于整个数组形成了一个山峰,山峰的左边是升序,山峰的右边是降序。我们发现 f(x) 的值空间就只有三种情况:
- 山峰左边的元素满足 A[i-1] < A[i] < A[i+1],可以把这种关系记录为 -1;
- 山峰元素满足 A[i-1] < A[i] && A[i] > A[i+1],可以把这种关系记录 0;
- 山峰右边的元素满足 A[i-1] > A[i] > A[i+1],可以把这种关系记录为 1。
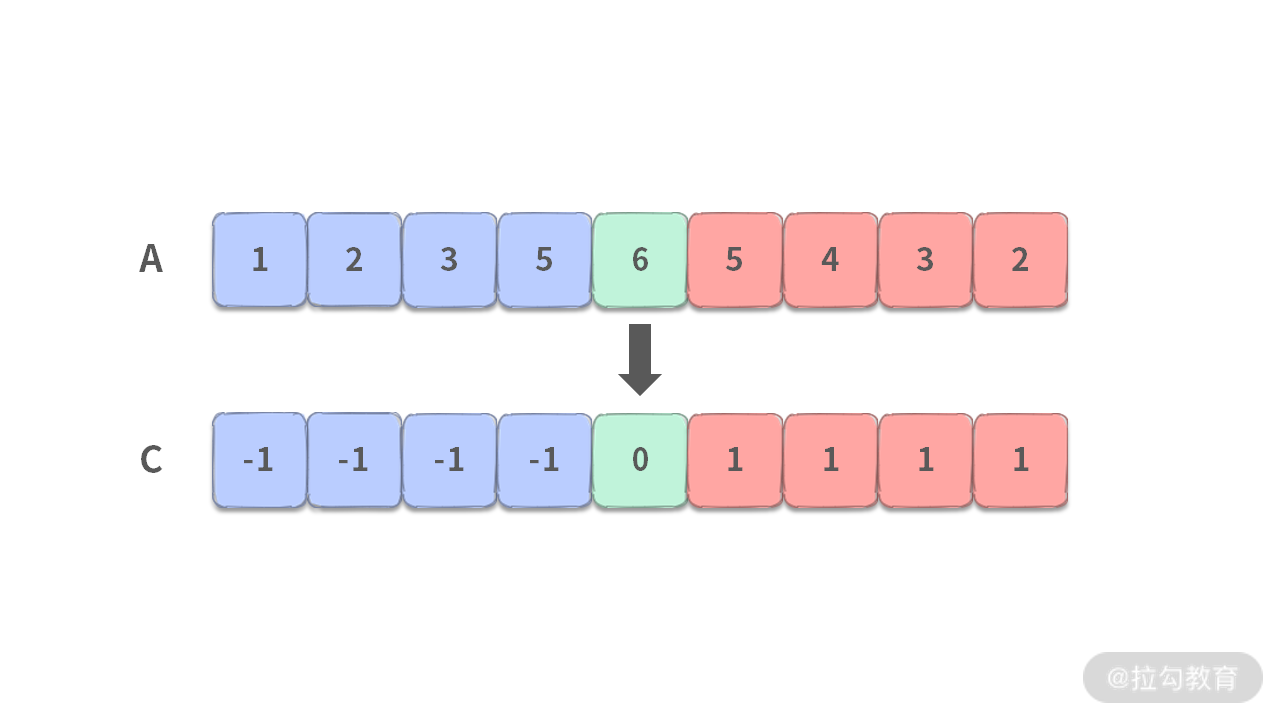
经过再次映射,就可以得到 C 数组,此时,C 数组就是一个有序的数组了。最终确定 f(x) 可以映射成一个有序数组 C[] = {-1, -1, 0, 1, 1, 1}。
此时我们我们已经可以补全 f(x) 函数了,如下所示:
int f(int m) {if (A[i - 1] < A[i] && A[i] < A[i + 1]) {return -1;}if (A[i - 1] < A[i] && A[i] > A[i + 1]) {return 0;}return 1;}int l = 1, r = N-1;while (l < r) {final int m = l + ((r-l)>>1);final int mov = f(m);}
在写代码时,还有一个问题待定:到底应该使用 lowerBound 还是 upperBound?提问破题法的第四步:最优解 0 在 C[] 的最左边还是最右边,决定使用 lowerBound 还是 upperBound。
比如在这里 C[] = {-1, -1, 0, 1, 1, 1}。山峰元素就只有一个,可以认为是一个最左边的元素,那么只需要用 lowerBound 就可以了。
转念一想,那么岂不是要先遍历一遍生成 C 数组?实际上没有必要,这个映射关系可以通过函数来完成。每次要获取的时候,就生成 C[i] 的值好了。
【代码】到这里我们已经可以写出代码了(解析在注释里):
int getC(int[] A, int i) {if (A[i - 1] < A[i] && A[i] < A[i + 1]) {return -1;}if (A[i - 1] < A[i] && A[i] > A[i + 1]) {return 0;}return 1;}int peakIndexInMountainArray(int[] A) {if (A == null || A.length < 3) {return -1;}int l = 1, r = A.length - 1;while (l < r) {final int m = l + ((r - l) >> 1);final int mov = getC(A, m);if (mov < 0) {l = m + 1;} else {r = m;}}return l;}
复杂度分析:时间复杂度 O(lgN),空间复杂度 O(1)。这里比较有趣的是,映射数组 C[] 并不需要构建,而是通过一个函数 getC 生成的。
【小结】这里我们总结一下提问破题法。
- 第一步:要什么,什么就是 x。
- 第二步:满足约束条件的 f(x) = 0。
- 第三步:不满足约束条件的 f(x) 设置为 -1 或者 1。
- 第四步:最优解 0 在 C[] 的最左边还是最右边,决定使用 lowerBound 还是 upperBound。
接下来,我们看一些练习题,在头条和美团的面试中都遇到过这个题目。希望你可以在课下尝试解答一下,如果有什么疑问,也可以写在留言区,我们一起讨论。
练习题 3:给定一个有序数组,找出数组中下标与值相等的那些数。
练习题 4:给定一个有序数组,找出数组中下标与值相等的数的范围。
如果从考点上来说,x 和 f(x) 还可以进行一些变化。我们还需要进一步深挖这个考点,以应对面试中可能出现的变形。
例 3:最小长度连续子数组
【题目】一个正整数数组 A,以及正数 s,找出最小长度的连续子数组,使得子数组和 >= s。
输入:A = [5, 2], s = 3
输出:1
解释:数组中存在长度为 1 的子数组 [5],其和大于给定数 3。
【分析】提问破题法的四步法我们依次使用出来。
1. 第一步:要什么,什么就是 x。
最小长度的连续子数组,使得子数组和 >= s

我们要求的是 “最小长度的连续子数组”。不过在实施的时候,需要把 “最小,最大” 这种字样去掉,然后变为 x。

确定了 x 之后,我们还需要确定 x 的范围。连续子数组的长度,在这个题里面只能可能是 [1, N + 1)。因为 A[] 数组和 s 都是正数。所以最短的连续子数组不可能为 0。 而最长可以是整个数组 N。那么用开闭原则表示就应该是 [0, N + 1)。
2. 第二步:满足约束条件的 f(x) = 0。

对于一个给定的子数组长度 x,f(x) 表示的含义:满足约束条件(长度为 x 的连续子数组的和的最大值 >= s),f(x) = 0。
3. 不满足约束条件的 f(x) 设置为 -1 或者 1。
那么到底是设置为 -1,还是 1 呢?这个时候我们需要回到题目的场景中进一步思考。此时可以确定 f(x) = 长度为 x 的子数组最大和。接下来可以得出:f(x + 1)≥f(x)
证明:当已经得到 f(x) 之后,只需要在长度为 x 的子数组的左边 / 右边再加延长一下就可以得到 f(x+1)。如下图所示:
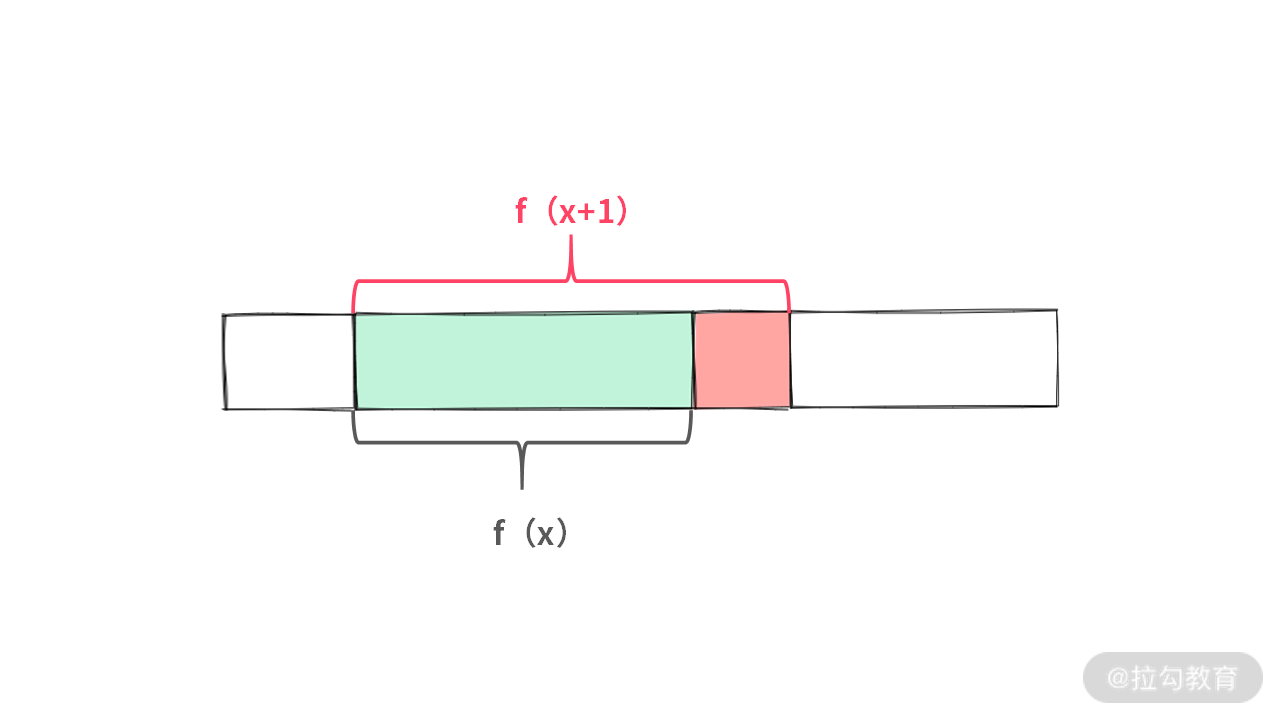
由于数组中的元素都是正数,那么可以肯定的是 f(x + 1) ≥ f(x)。那么我们可以得到一个单调递增的函数,那就是:
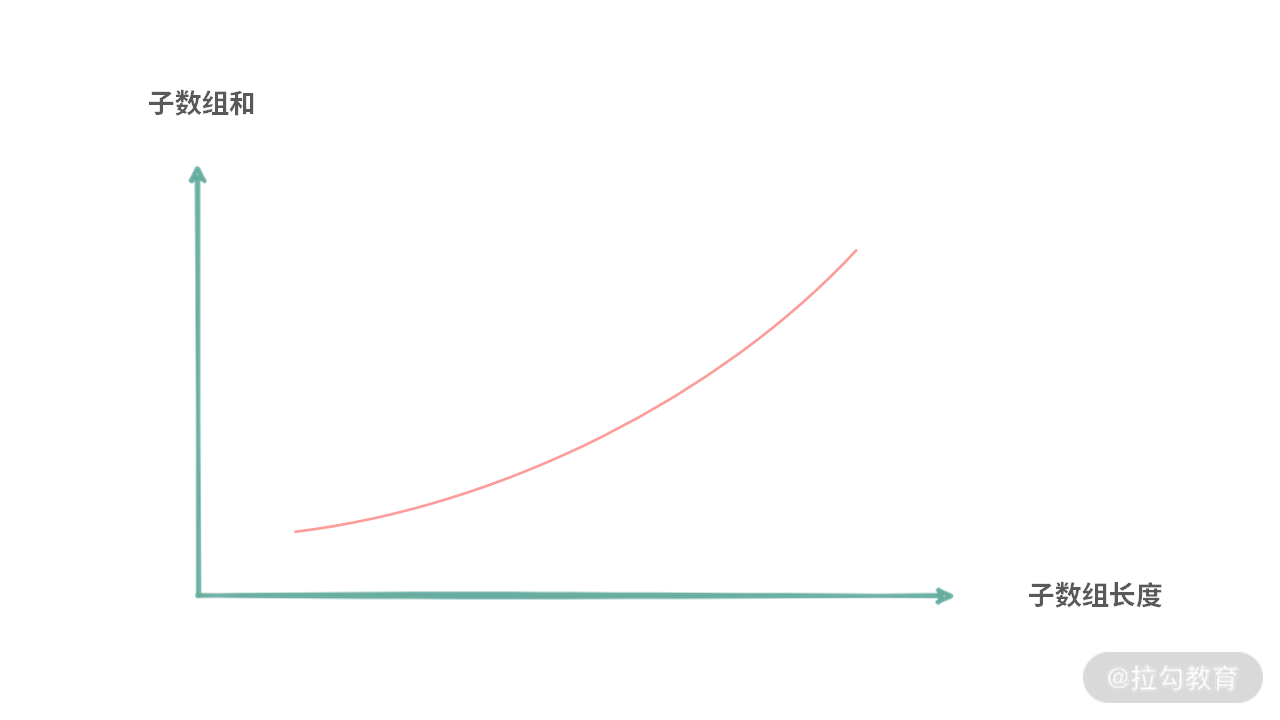
那么子数组的和实际上只有 2 种情况:
- 小于 s,此时可以设置 f(x) = -1;
- 大于等于 s(这道题只需要求大于等于,所以这里把等于和大于合在一起)f(x) = 0。
如果把 f(x) 看成一个映射,那么映射之后的数组 C[] = {-1, -1, 0, 0, 0}。
4. 最优解 0 在 C[] 的最左边还是最右边,决定使用 lowerBound 还是 upperBound。
按照题目要求,需要找到的是长度最小的连续子数组,实际上就是在 C[] 数组中找到最左边的 0,所以应该用 lowerBound。
【代码】到此为止,我们已经能够写出代码了(解析在注释里):
int getC(int[] A, int len, int s) {long sum = 0;final int N = A == null ? 0 : A.length;for (int i = 0; i < N; i++) {sum += A[i];if (i < len - 1) {continue;}if (sum >= s) {return 0;}sum -= A[i - (len - 1)];}return -1;}int minSubArrayLen(int s, int[] A) {final int N = A == null ? 0 : A.length;int l = 1, r = N + 1;while (l < r) {final int m = l + ((r - l) >> 1);final int mov = getC(A, m, s);if (mov < 0) {l = m + 1;} else {r = m;}}return l > N ? 0 : l;}
复杂度分析:搜索空间长度为 N 并且有序,在里面二分的时候,只需要运行 O(lgN) 次。而在每次 getC 获取映射值的时候,复杂度为 O(N)。那么时间复杂度为 O(NlgN),空间复杂度为 O(1)。
【小结】到这里,我们已经可以总结出二分搜索比较通用的提问破题法了,通过提问来确定:
- 确定搜索空间,即 x 的范围;
- 确定 f(x) 是否有序。有可能你还需要一个简单的证明。
这里我们可以再看一下下面这几个练习题。
练习题 5:包含所有子串的最短子串。给定两个字符串 A,B。要求在字符串 A 中找到一个最短的子串,在这个子串中包含了所有的 B 中的字符。
注:我们使用了复杂度为 O(NlgN) 的二分搜索来求解例 3 和练习题 5,实际上有 O(N) 的求解办法,你能想一下吗?(关于这块内容,我们将在 “第 10 讲” 中详细介绍)。
例 4:最大平均值
【题目】给定一个正整数数组 A 和 k,要求找到子数组,输出其最大平均值,并且子数组长度要满足大于等于 k。
输入:A = [1,12,-5,-6,50,3], k = 3
输出:15.667
解释:在所有长度大于等于 3 的子数组中,(-6 + 50 + 3) / 3 = 15.667 是最大的。
【分析】提问破题法的四步法我们依次使用出来。
1. 第一步:要什么,什么就是 x
输出子数组最大平均值,并且子数组长度 >= k。
要输出的是子数组的最大平均值,所以搜索空间 x 就是连续子数组的平均值,如下图所示:
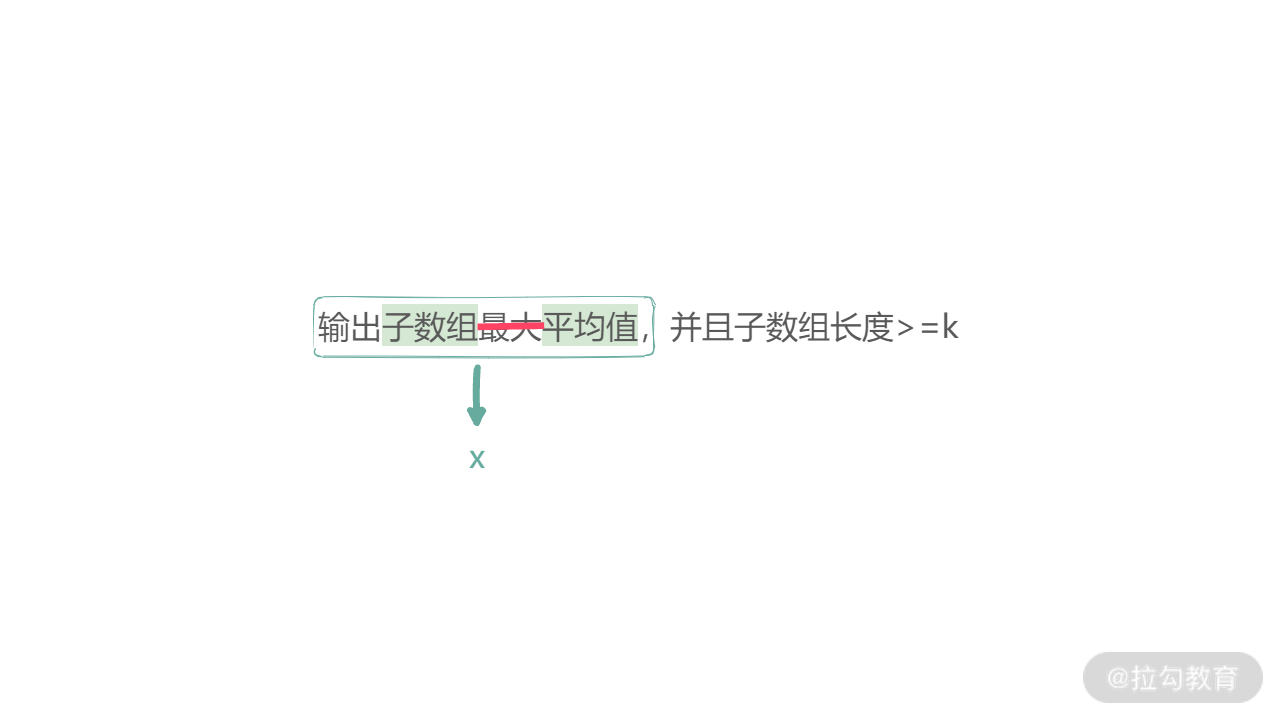
再看一下范围:x 的最小值,就是数组的最小值。而 x 的最大值,就是数组的最大值。
如果是在面试时,那么我们已经可以写出如下代码框架了:
int small = Integer.INT_MIN;int large = Integer.INT_MAX;for (int i = 0; i < N; i++) {small = Math.min(small, A[i]);large = Math.max(large, A[i]);}double l = small, r = large + 1;while (l < r) {double m = (l + r) / 2.0;double mov = ? ?if (mov < ? ?) {l = m + 1;} else {r = m;}}
剩下的就是需要找到 f(x)。
2. 第二步:满足约束条件的 f(x) = 0。

对于 f(x) 来说,其含义为:给定的平均值 x,如果存在:
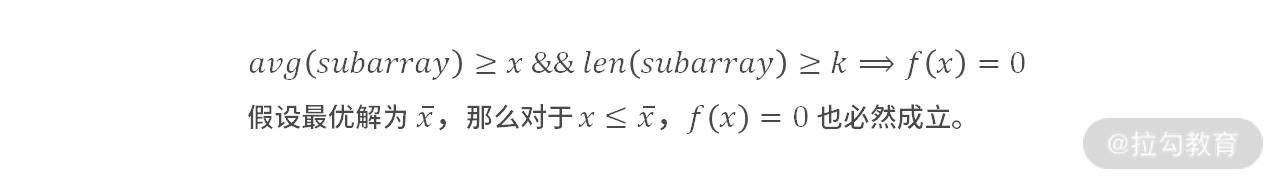
3. 不满足约束条件的 f(x) 设置为 -1 或者 1。

4. 最优解 0 在 C[] 的最左边还是最右边,决定使用 lowerBound 还是 upperBound。
由于我们求解最大平均值,就是找到满足条件的最大的 x。也就是 C[] 数组里面的最右边的 0。此时应该使用 upperBound 的模板。
难点:f(x) 函数的代码。
我们之前写过的代码里面,f(x) 都比较直观,比较容易写。但是这道题里面。你先弄懂如下问题 1,才能继续往后思考。
问题 1:给定的平均值 x,是否存在连续子数组平均值 >= x,并且长度 >= k
要解决这个问题,我们不妨把问题化简一下。把子数组长度 >= k 去掉,看看可不可以简单一点,如果可以,那么我们就可以从简单一点的问题入手。问题就变成如下问题 2。
问题 2:给定的平均值,是否存在连续的子数组平均值 >= x
平均值最后是平均到每个元素身上的。那么我们事先从数组 A[] 中将这个平均值 x 减掉。用代码可以表示如下:
int B[] = new int[A.length];for (int i = 0; i < A.length; i++) {B[i] = A[i] - x;}
如果要找到 “连续的子数组的平均值>= x”,实际上就变成在 B[] 数组上找到一个连续的子数组,要求其和 >= 0。如果我们能找到 B[] 数组上的连续子数组的最大和,再看一下这个最大和是否 >= 0 就可以了。这样问题已经变成求一个数组的最大子数组和,如下问题 3。
问题 3: 给定一个数组 B[],求这个数组上的最大子数组和。
在解决问题 3 时,我们采用一种落差法,求出 B[] 数组的前缀和数组 C[],所以说前缀和数组,即 C[i] = B[0] + B[1] + .. + B[i]。当得到 C[] 数组之后,C[i] 与 min(C[0], …. , C[i-1]) 的差就是以 B[i] 结尾的连续子数组的最大和。用图表示如下:
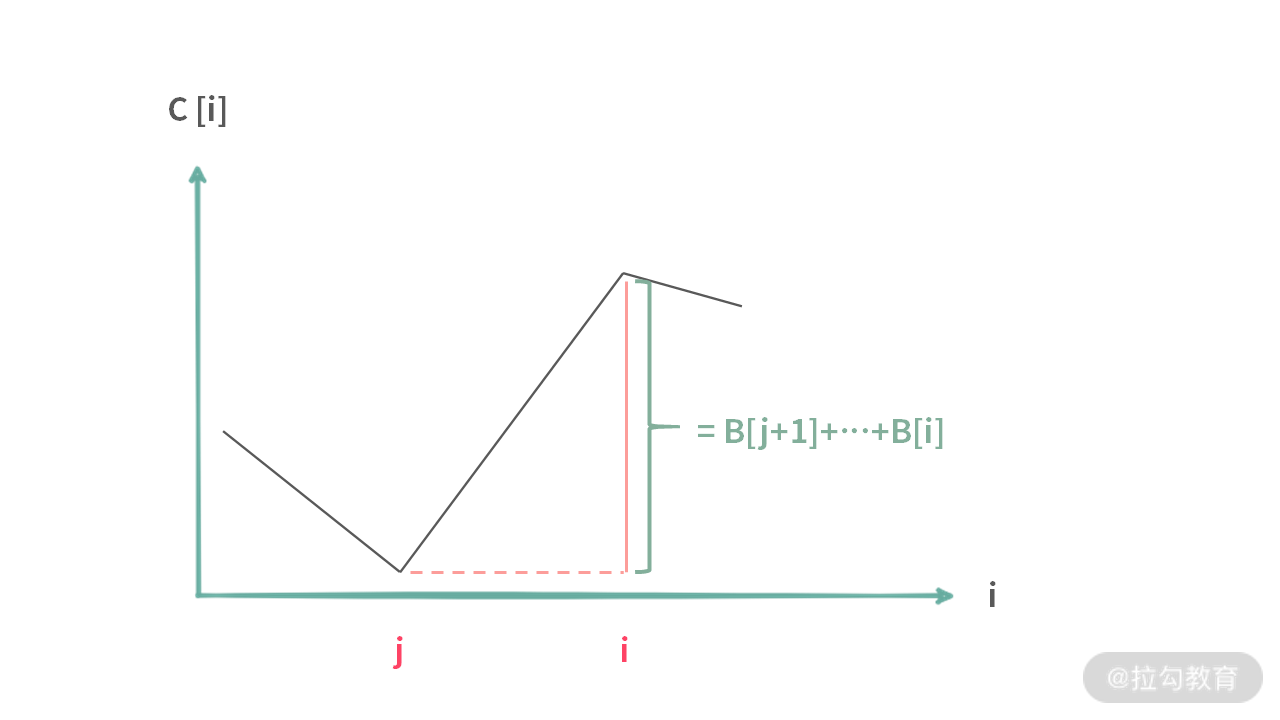
那么问题 3 可以求解如下(解析在注释里):
int Q3(int[] B) {final int N = B == null ? 0 : B.length;long pre = 0;long pre_min = 0;long ans = Integer.MIN_VALUE;for (int i = 0; i < N; i++) {pre += B[i];ans = Math.max(ans, pre - pre_min);pre_min = Math.min(pre_min, pre);}return (int)ans;}
有了问题 3 的求解,我们就可以返回去求解问题 2。只需要在问题 3 的基础上做如下操作即可。
boolean Q2(int[] A) {if (Q3(A) >= 0) return true;return false;}
接下来,我们再返回去看问题 1。当我们仍然利用 A[] 数组中的每个元素减去 x 得到 B[] 数组之后,问题 1 等价于以下问题 4。
问题 4: 给定一个数组 B[],是否存在长度 >= k 的连续子数组,其和 >= 0。
这里多加的一个条件 “长度>= k”,实际上是要求:
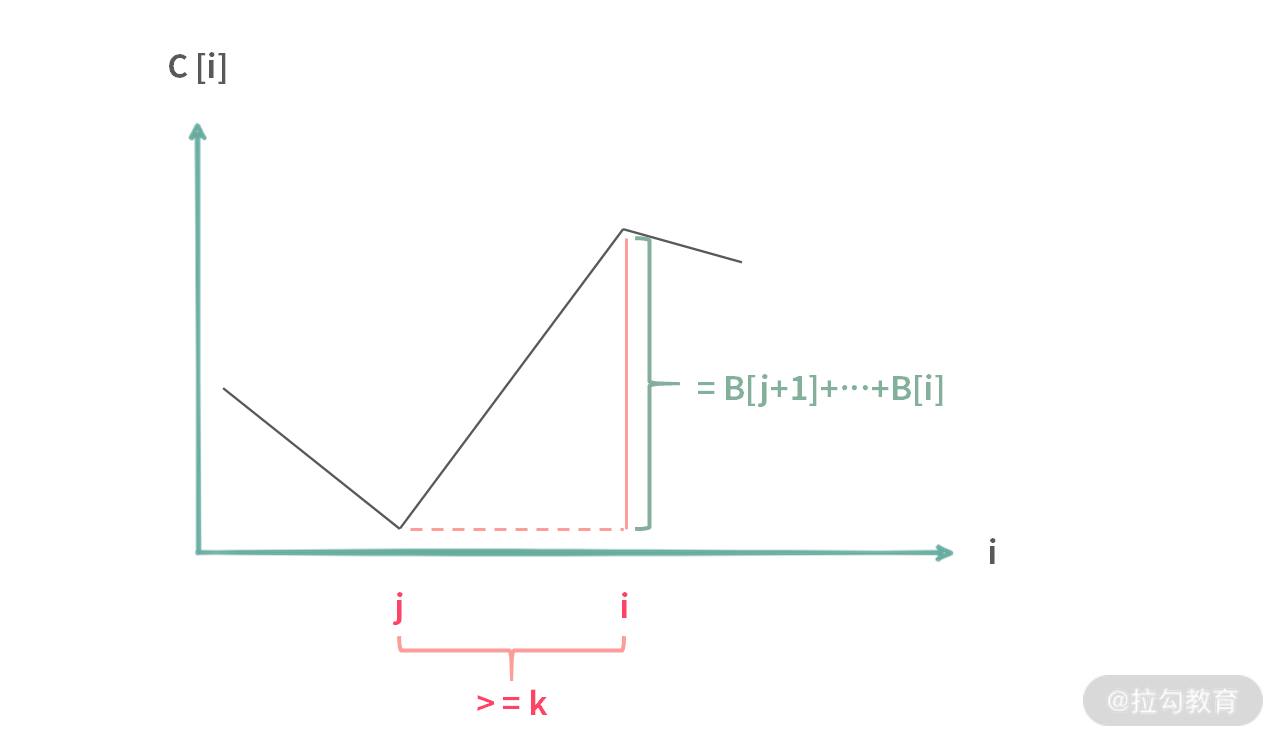
也就是 j 和 i 的距离要 >= k。这里就需要用到滑动窗口的方法了。可以将代码写为如下的样子(解析在注释里):
int Q4(int[] A, double m, int k) {final int N = A == null ? 0 : A.length;int[] B = new int[N];int[] C = new int[N];for (int i = 0; i < N; i++) {B[i] = (double)A[i] - m;}C[0] = B[0];for (int i = 1; i < N; i++) {C[i] = C[i - 1] + B[i];}double pre_min = 0;for (int i = k - 1; i < N; i++) {if (C[i] >= pre_min) {return 0;}pre_min = Math.min(pre_min, C[i + 1 - k]);}return 1;}
到这里,我们已经求解出 f(x)。
【代码】根据前面的分析,相信你已经可以根据思路写出代码了(解析在注释里):
int getC(int[] A, double[] B, double m, int k) {final int N = A == null ? 0 : A.length;for (int i = 0; i < N; i++) {B[i] = (double)A[i] - m;}for (int i = 1; i < N; i++) {B[i] += B[i - 1];}double pre_min = 0;for (int i = k - 1; i < N; i++) {if (B[i] >= pre_min) {return 0;}pre_min = Math.min(pre_min, B[i + 1 - k]);}return 1;}double maxAverage(int[] A, int k) {final int N = A == null ? 0 : A.length;int small = Integer.MAX_VALUE;int large = Integer.MIN_VALUE;for (int i = 0; i < N; i++) {small = Math.min(small, A[i]);large = Math.max(large, A[i]);}double[] B = new double[N];double l = small;double r = (double)large + 1.0;while (r - l > 1e-6) {double m = (l + r) / 2.0;int mov = getC(A, B, m, k);if (mov <= 0) {l = m;} else {r = m;}}return Math.abs(l) < 1e-6 ? 0 : l;}
复杂度分析:upperBound 主循环部分为 O(lgN),但是在每次 getC 函数执行时,其复杂度为 O(N)。所以时间复杂度为 O(NlgN),空间复杂度为 O(N)。
【小结】写出这道题之后,这里我们再总结一下这道题的考点,如下图所示:
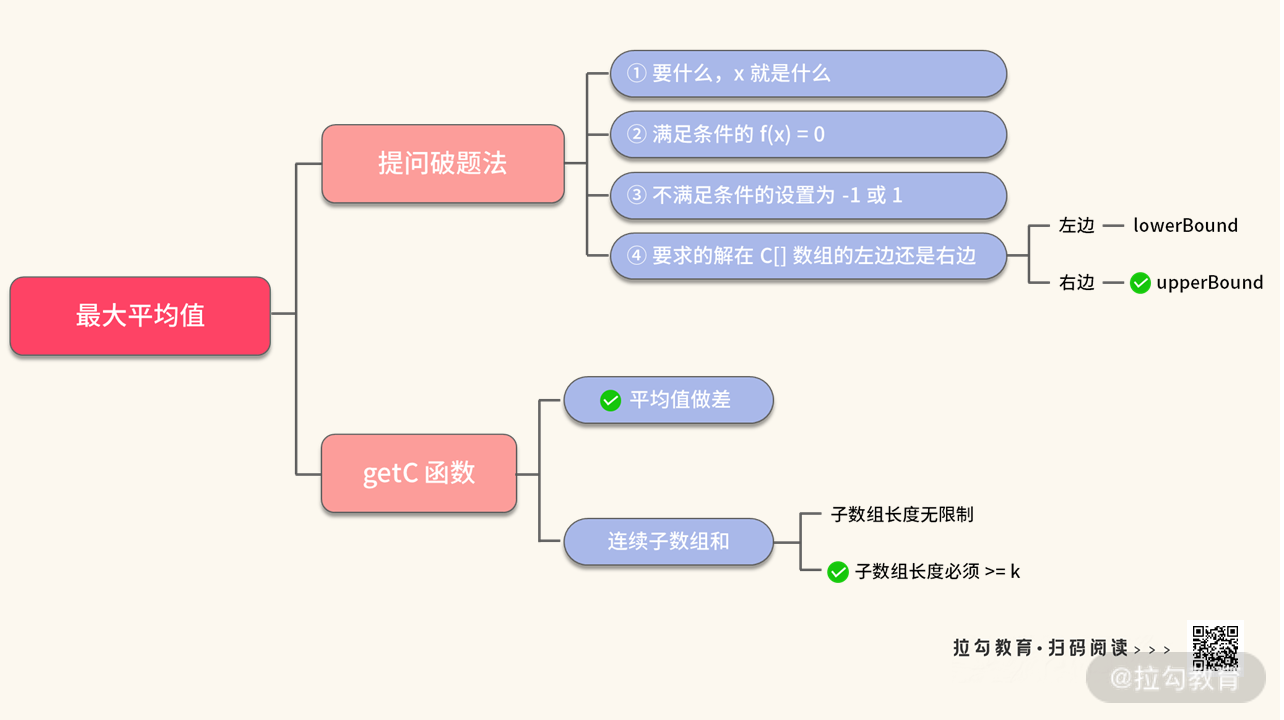
这道题的考点无非就是将连续子数组和与二分搜索组合了一下,只要你熟练地掌握这 2 个关键技能,击破这类面试题就不难了。
关于二分搜索的扩展,我们已经讲了很多,那么就这道题而言,是否还有可以深挖的点呢?比如:连续子数组求最大平均值的小技巧就是每个元素减去平均值。我们可以将题目变成连续子数组的最大和问题。而连续子数组的最大和问题又可以分出 4 种情况。
1. 长度无限制,是最常见的连续最大子数组和问题。这里我们采用落差法来求解,也可以利用双指针或者 DP 来进行求解(这两种解法分别会在 “第 10 讲” 和 “第 14 讲” 详细讲解)。
2. 连续子数组的长度必须等于 k。采用滑动窗口法来求解。
3. 长度 >= k 的连续子数组,采用滑动窗口 + 落差法来求解。代码参考前面例题 4 的代码。
4. 如果限制长度必须要 <= k 的连续子数组的最大和,这个时候应该怎么办?
三步切分法
前面介绍的提问破题法已经能够解决相当一部分问题了,下面我们再来看一下二分搜索的最后一种面试中的常考题型——切分题,这种题目比较适合使用切分法。
所谓切分法,顾名思义就是把搜索范围分为两半,然后把我们不想要的那部分搜索区域切掉(扔掉),也可以叫三步切分法:
- 找出一个分界元素;
- 将有序的搜索空间分为两半(复杂度为 O(1)),扔掉不需要的那一半;
- 在剩下的空间中递归使用切分法。
实际上在 “第 08 讲” 里面,我们介绍三路切分的时候,也用到了切分法的思路。这里我们将两者做个对比。
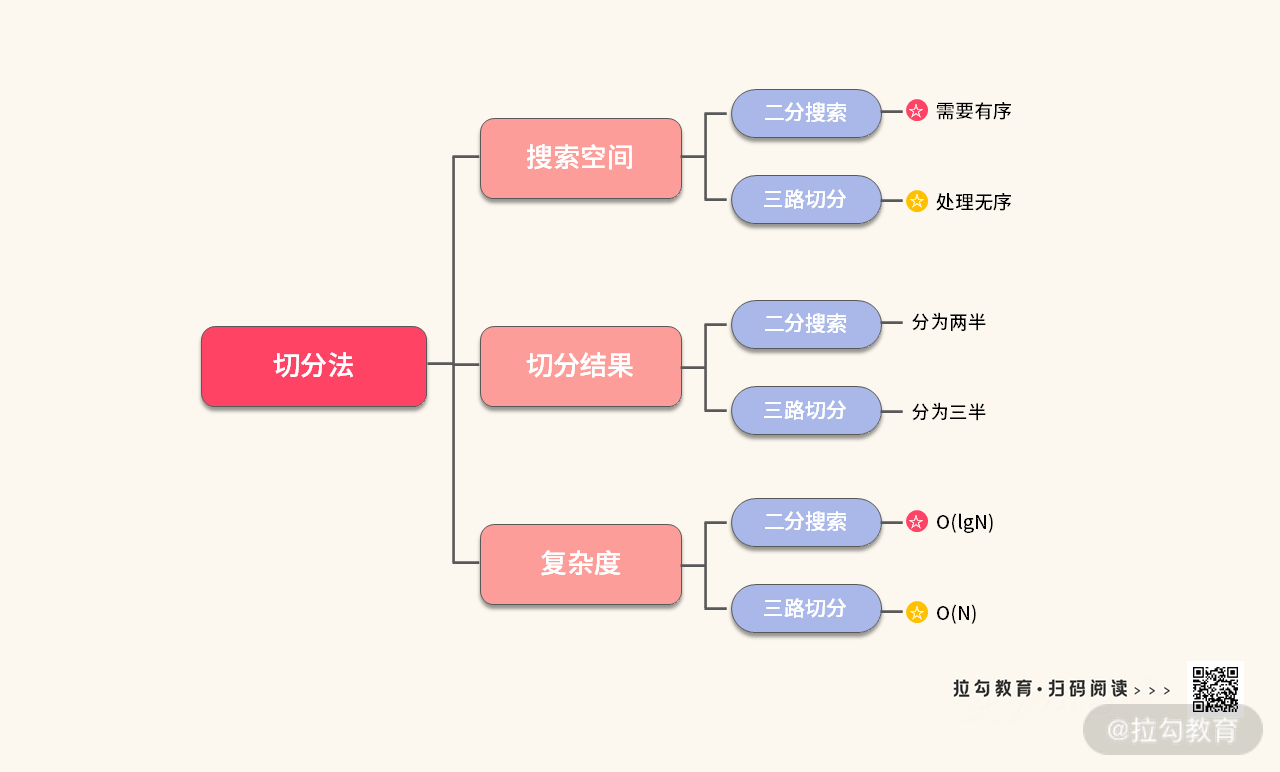
二分搜索和三路切分都可以不停地缩小搜索空间,但是两者的使用条件也不太一样:
- 二分搜索需要有序性,复杂度为 O(lgN);
- 三路切分不需要有序性,复杂度为 O(N)。
在标准的模板代码 lowerBound 和 upperBound 里面,我们在查找时,都使用了切分法切掉我们不想要的搜索空间,只在剩下的搜索空间里面继续搜索。
不过,对于有的面试题来说,有序性并不会给得那么赤祼祼,此时就需要利用三步切分法的帮助。下面我们一起通过例题看看怎么运用切分法。
例 5:旋转数组的查找
【题目】给定一有序数组 A(没有重复元素),某个位置发生了旋转,给定元素 x,请输出 x 在数组 A 中的下标。如果不存在,输出 -1。
输入:A = [1, 2, 3, -1, 0], x = 3
输出:2
解释:因为 A[2] == 3 所以返回下标 2
【分析】这里如果我们要使用二分搜索来解决这个问题。面临的最大问题是,数组并不是有序的。如果将数组的值画在坐标轴上,那么形成的效果可能是:
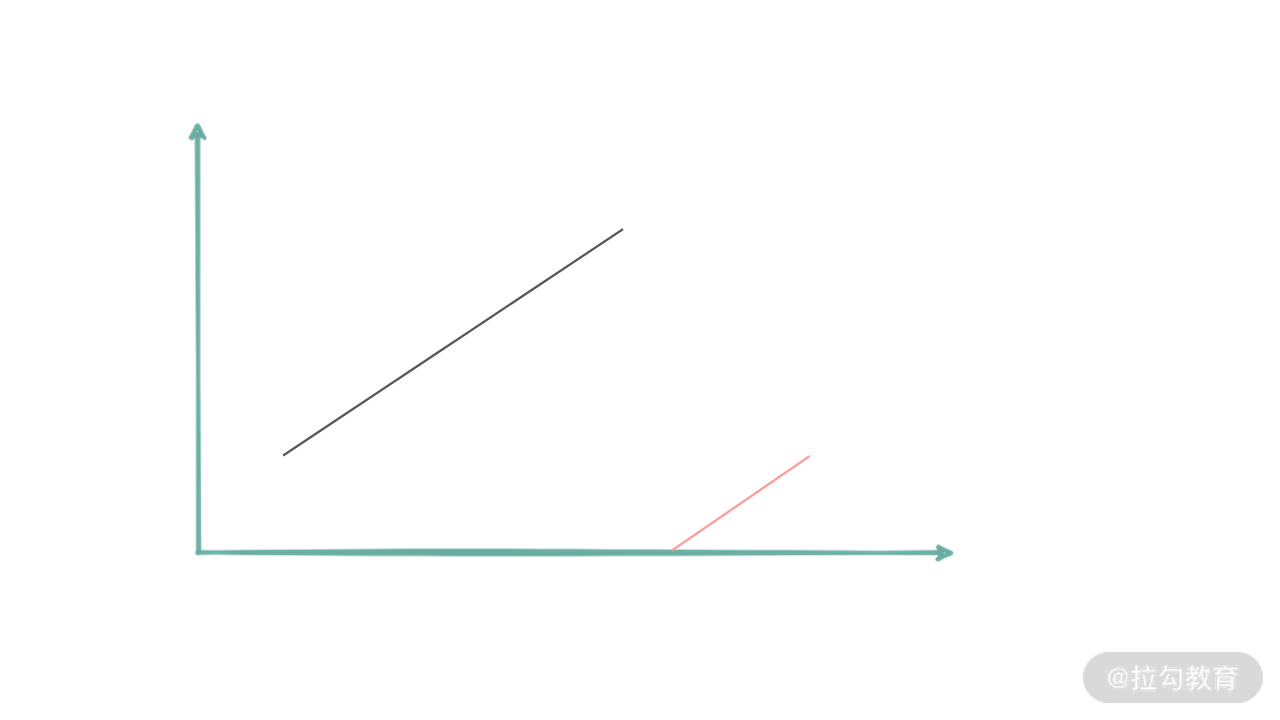
但是,我们很快可以发现,虽然整个数组不是有序的,但是数组的两个部分分别是有序的。这个信息很关键,如果能够利用上,就一定能够破题。
在进行二分搜索的时候,我们首先是需要取中间值。
final int m = l + ((r-l)>>1);
那么此时我们已经知道了 A[L]、A[M]、A[R] 三个值,可以在进一步二分之前加一个处理。
if (A[l] == x) return l;if (A[m] == x) return m;if (A[r-1] == x) return r-1;
通过这样的处理之后,后面我们在进行二分操作的时候,会更加简单一点。接下来我们再看 A[M] 的值,A[M] 有两种可能:一种是掉落在左边,一种是掉落在右边区域。
1. A[m] 掉落在左边区域。如下图所示:
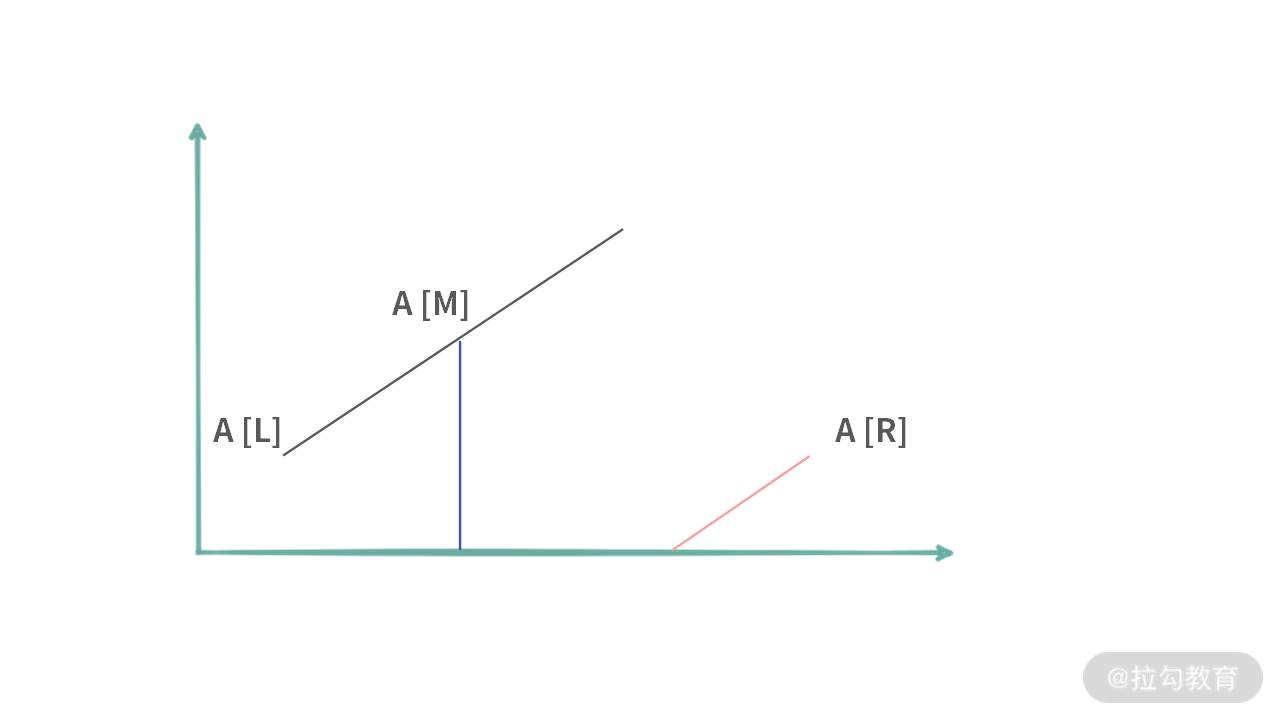
当 A[L] < A[M] 的时候,中间值肯定是掉落在左边的。在这种情况下,我们需要再分 (a)、(b) 两种情况。
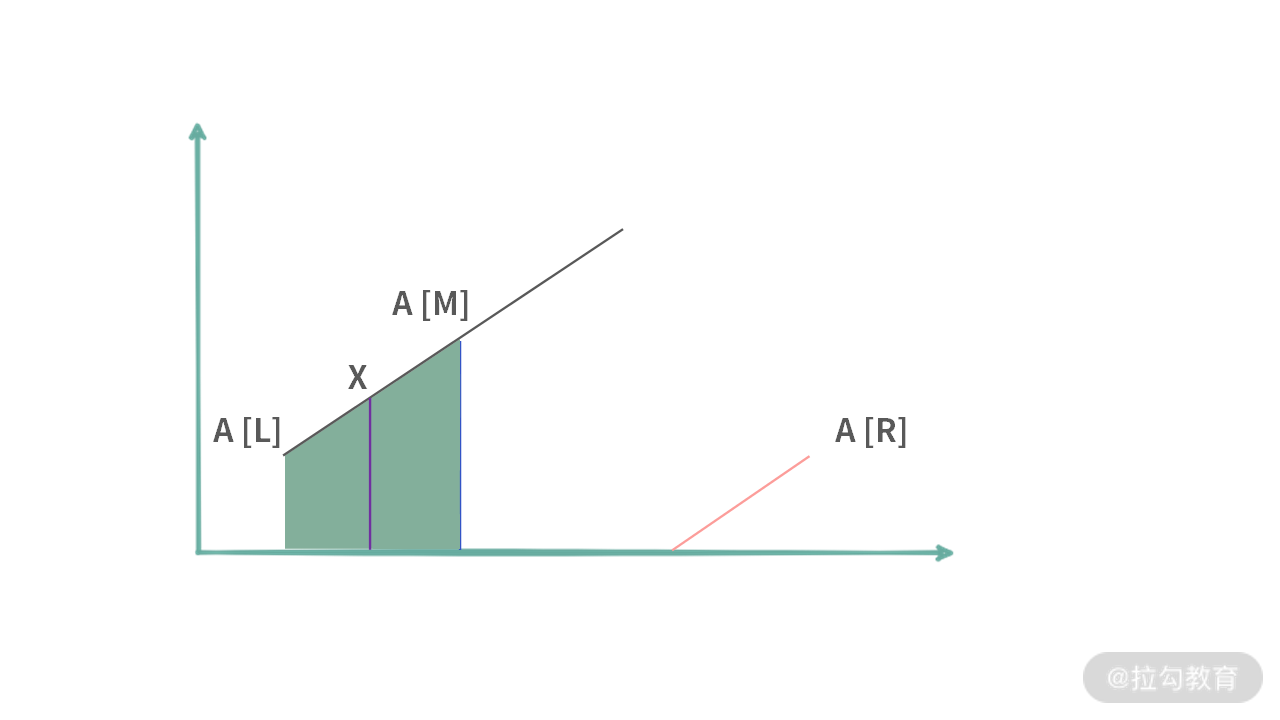
(a)x 位于 A[m] 的左边。此时需要满足条件:A[L] < x < A[M]。在这种情况下,右边的区域是没有必要保留的。可以通过 R = M 来扔掉。
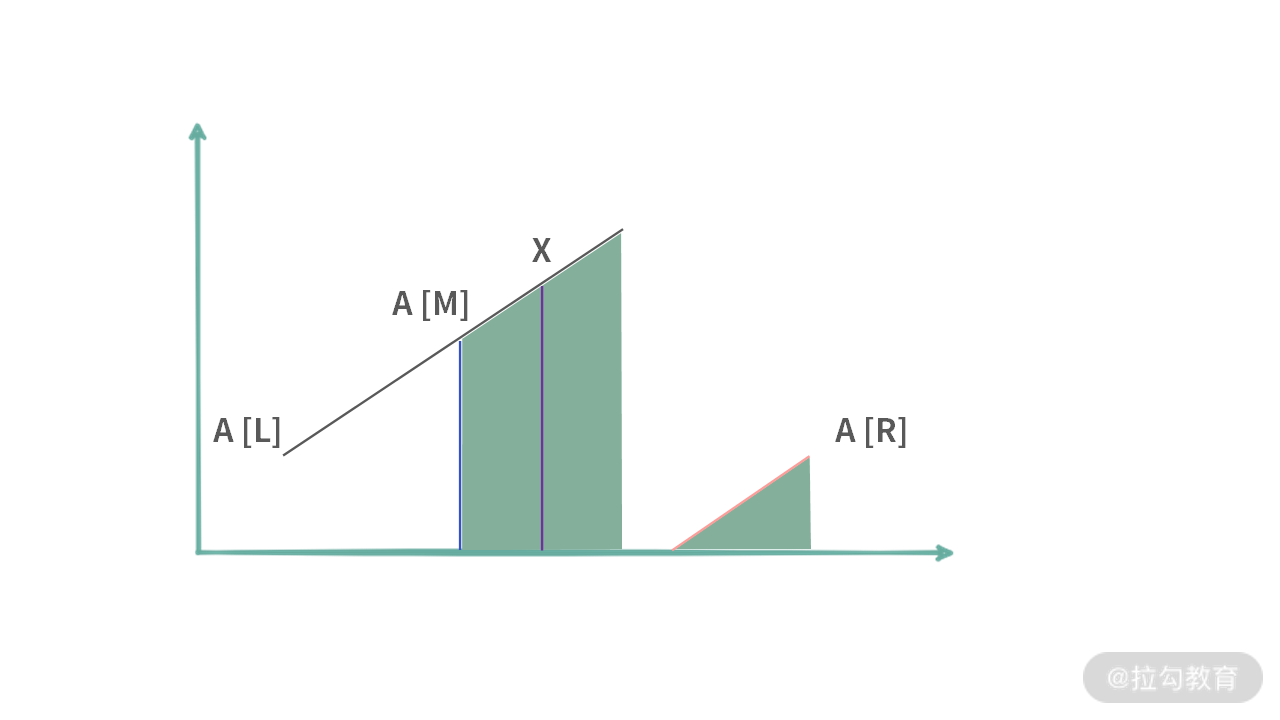
(b)x 位于 A[m] 的右边。此时左边的部分是没有必要保留的,把左边切掉,让 L = M+ 1。
2. A[m] 掉落在右边区域。需要满足条件 A[M] < A[R]。如下图所示:
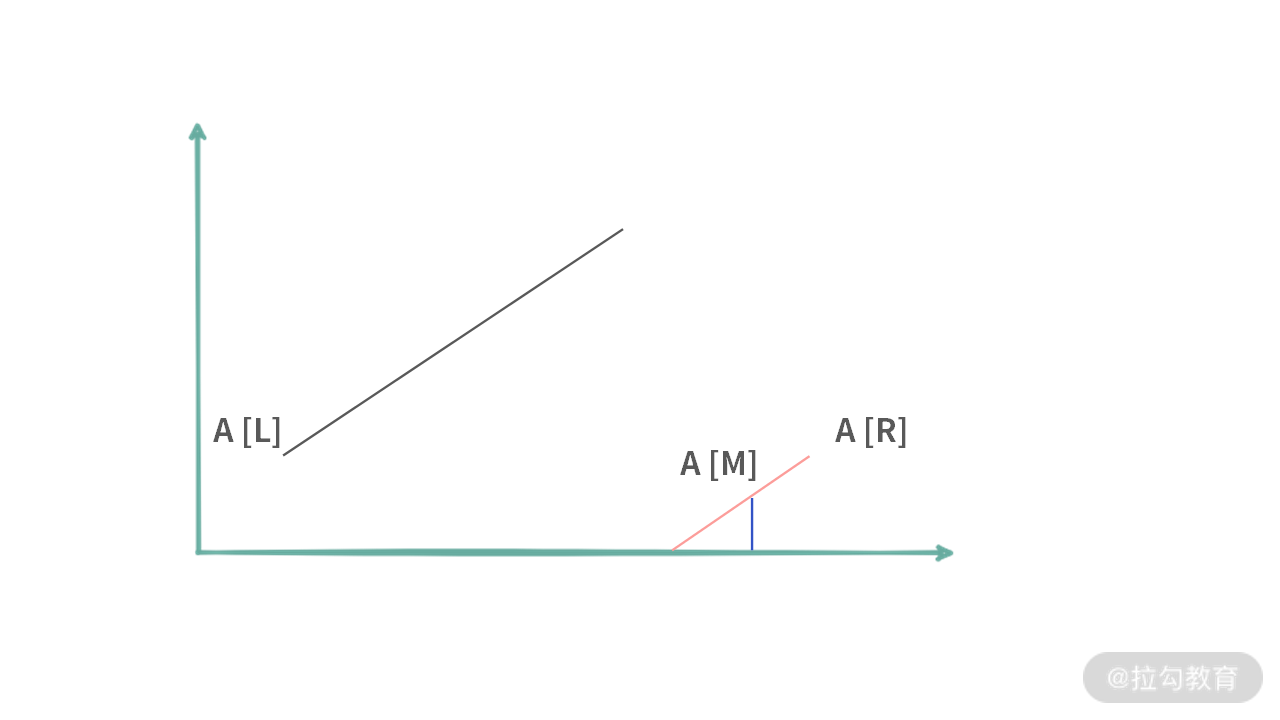
此时我们要找的值 x 可以分成(c)、(d)两种情况:
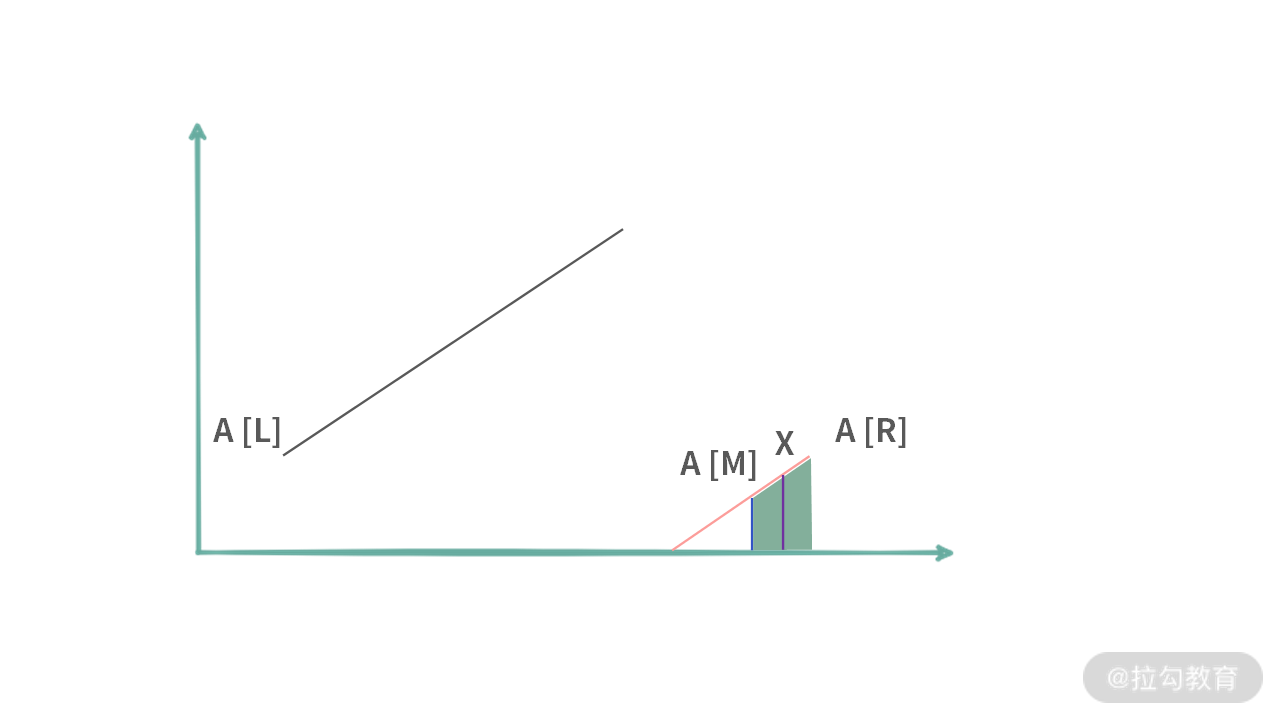
(c)位于最右边区域。此时需要满足条件,A[M] < x < A[R]。那么可以直接把左边区域扔掉,设置 L = M + 1 即可。
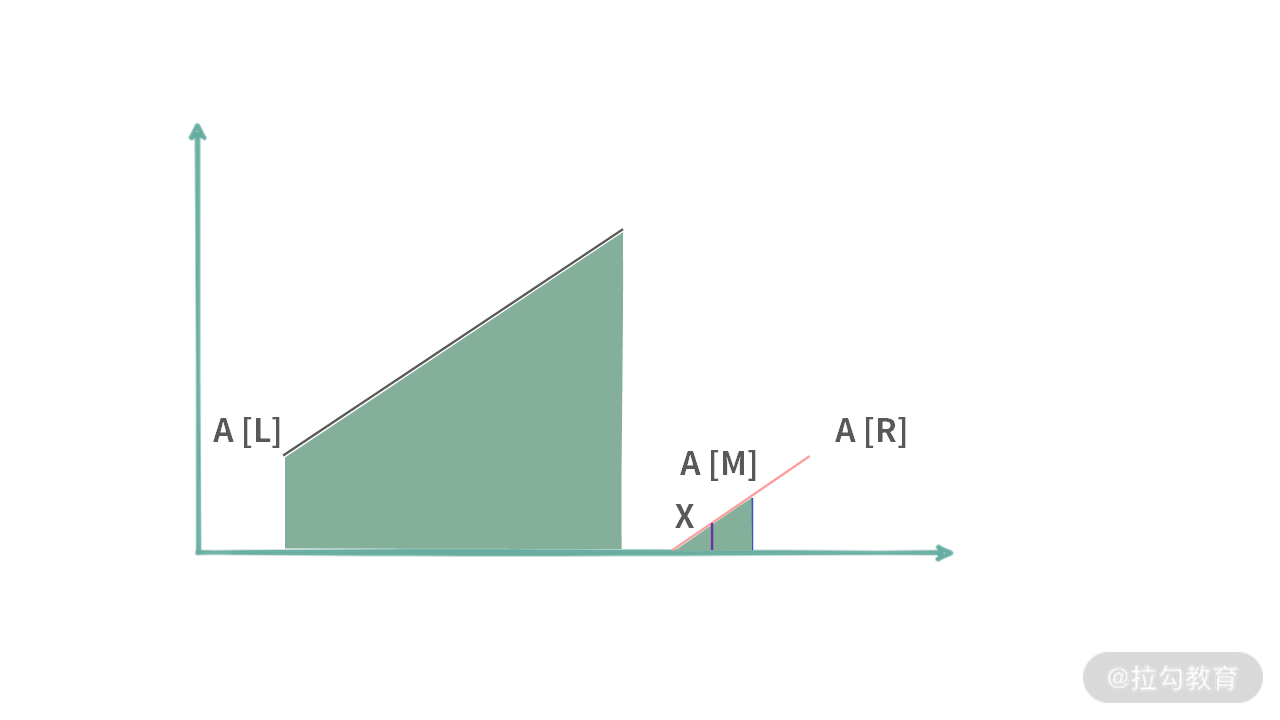
(d)位于左边区域,此时只需要把右边区域扔掉即可。即设置 R = M。
【代码】经过详细的分析,我们已经可以写代码了(解析在注释里):
int search(int[] A, int x) {final int N = A == null ? 0 : A.length;int l = 0, r = N;while (l < r) {final int m = l + ((r - l) >> 1);if (A[l] == x)return l;if (A[m] == x)return m;if (A[r - 1] == x)return r - 1;if (A[m] > A[l]) {if (A[l] < x && x < A[m]) {r = m;} else {l = m + 1;}} else {if (A[m] < x && x < A[r - 1]) {l = m + 1;} else {r = m;}}}return -1;}
复杂度分析:时间复杂度为 O(lgN),空间复杂度 O(1)。
【小结】虽然整个数组不是有序的,但是我们可以每次都在一个小范围里面利用二分进行搜索。
考点: 这道题的考点就是分清楚 (a)、(b)、(c)、(d)四种情况。要特别注意的是,在处理(a)、(b)两种情况的时候,要用 if 判断有序的部分,else 处理无序的部分。比如:
if (A[l] < x && x < A[m]) { }else { };
(c)、(d)两个条件的处理也是如此。
if (A[m] < x && x < A[r-1]) { }else { }
我在面试时,曾经遇到不少候选人在处理这四情况的时候没有想到上面这个小技巧,因此浪费了很长时间。
练习题 6:例 5 还可以利用前面我们介绍过的提问破题法来进行求解。你能想一下吗?
练习题 7:题目限制了没有重复元素,如果有重复元素,如何进行查找呢?
练习题 8:一个有序数组经过了旋转,请找出这里面最小的元素(有重复元素)。
总结
到这里我们已经可以总结一下二分搜索涉及的知识点了,如下图所示:
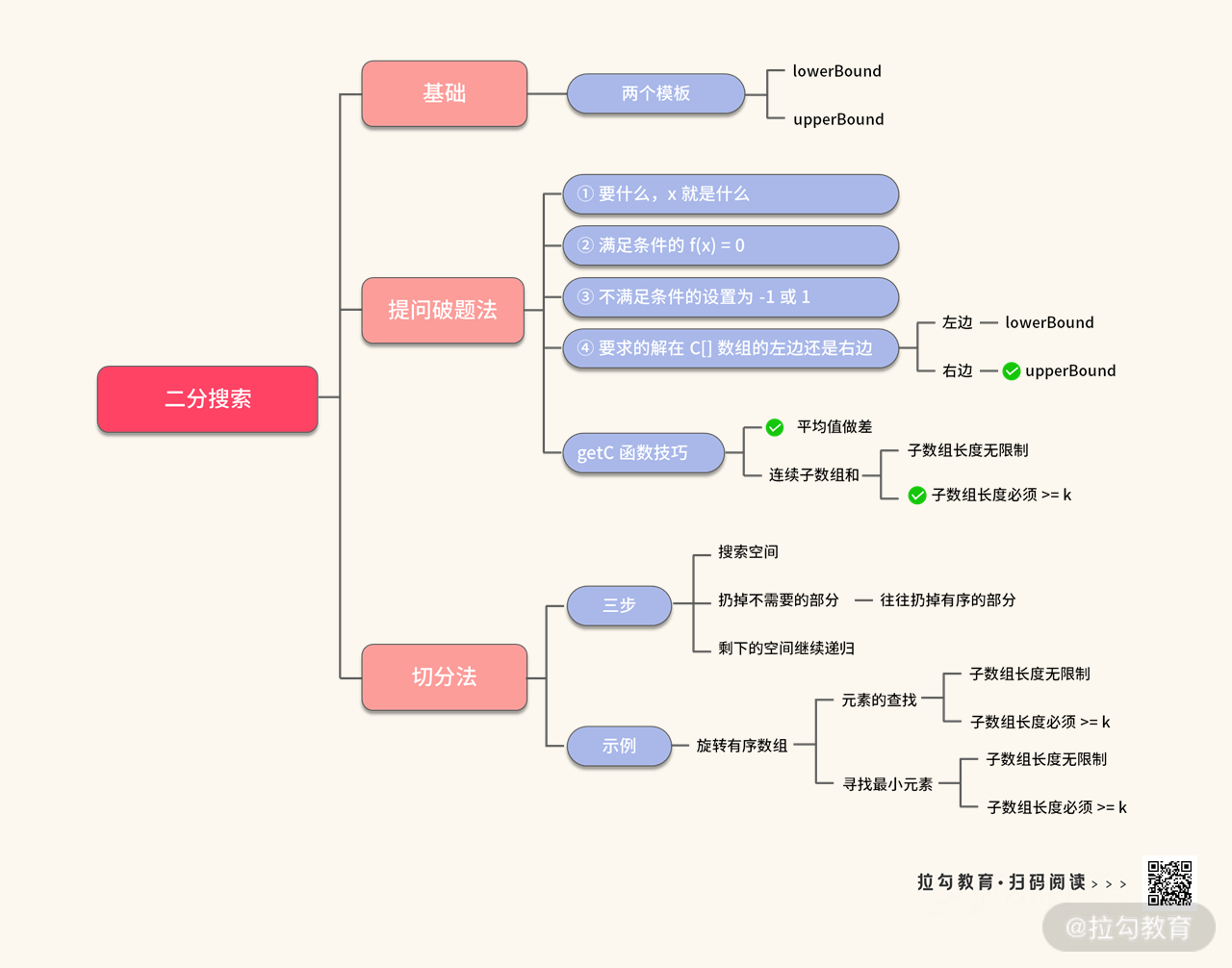
如果要顺利地解决二分搜索,那么:
- 首先你需要熟练地写出两个 lowerBound 和 upperBound 的模板
- 然后你需要学会应用提问破题法和切分法
掌握以上两个技巧,那么绝大部分涉及二分搜索的面试题就再也难不住你了。
思考题
我再给你留一道思考题:给定两个有序数组,请找出这两个有序数组的中位数。(是的,这是 “第 08 讲” 例 2)。不过我希望你能够用二分搜索的办法来进行求解。
接下来请和我一起踏上更加奇妙的算法旅程。让我们继续前进。下一讲将介绍 10 | 双指针:如何掌握解决最长,定长,最短区间问题的决窍。

