数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
今天开始进行算法模板的复习和整理。授人以鱼,不如授人以渔。在本讲,我的目的是教会你如何做知识的整理和模板的整理,而不是直接给你一些现成的东西,让你去死记硬背。无论是思维导图,还是代码模板,你自己整理一遍的收获会更大。
今天我们主要介绍两种方法:
- 通过思维导图将学过的知识添加到你的知识树中;
- 将刷过的题目整理成代码模板,放到你的代码模板库中。
排序
我们在学习排序的时候,主要讨论了合并模板和快速排序两种排序,现在就可以利用下面这个思维导图进行快速复习。
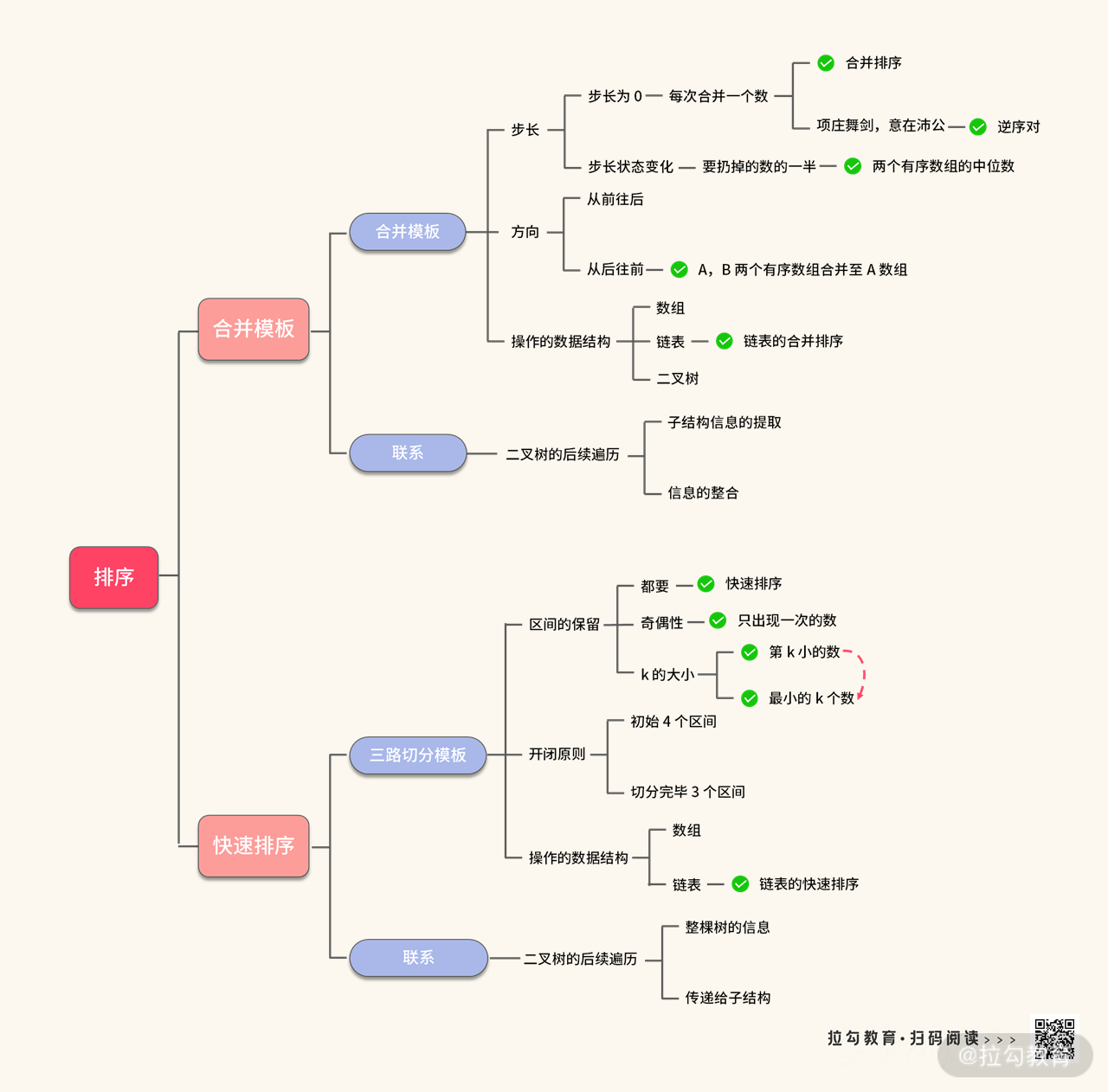
合并的技巧
对于合并排序来说,我觉得最重要的是掌握下面这段合并的小技巧:
int i = b;int j = m;int to = b;while (i < m || j < e) {if (j >= e || i < m && a[i] <= a[j]) {t[to++] = a[i++];} else {t[to++] = a[j++];}}
可以看到 while 语句中 if 语句的写法(上述代码第 11 行)用了最简洁的代码处理了各种边界条件!
三路切分
在《08 | 排序:如何利用合并与快排的小技巧,解决算法难题?》介绍快速排序时,三路切分也是一个高频出现的知识点,所以我们需要掌握这个代码模板,如下所示:
void swap(int[] A, int i, int j) {int t = A[i];A[i] = A[j];A[j] = t;}int threeSplit(int[] A, int b, int e) {if (b >= e) {return 0;}final int m = b + ((e - b) >> 1);final int x = A[m];int l = b;int i = b;int r = e - 1;while (i <= r) {if (A[i] < x) {swap(A, l++, i++);} else if (A[i] == x) {i++;} else {swap(A, r--, i);}}if (i - l == 1)return A[l];if (((l - b) & 0x01) == 1) {return threeSplit(A, b, l);}return threeSplit(A, i, e);}
二分
我们将二分的知识点整理如下:
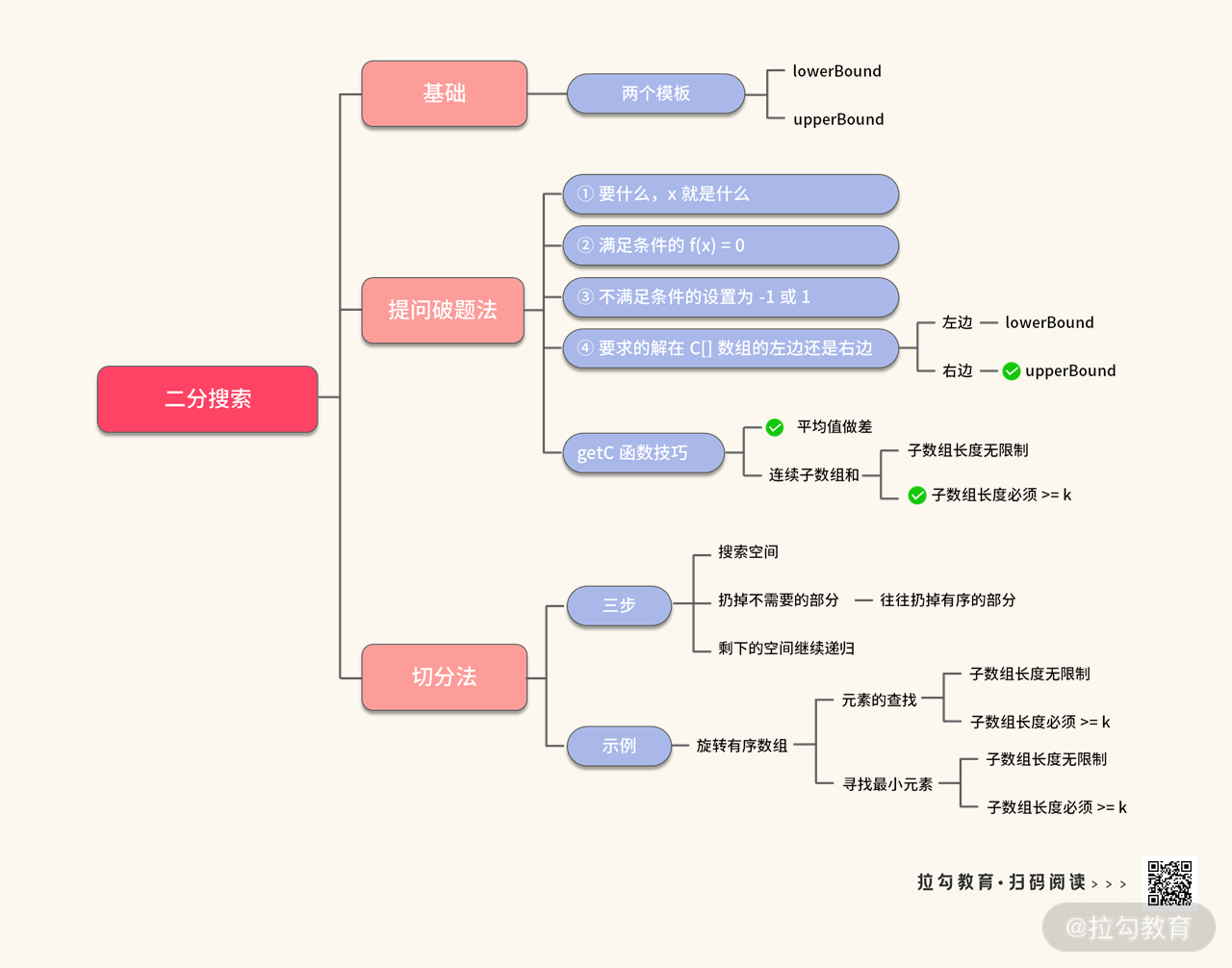
当已知一个题目可以用二分进行破解时,就可以使用 lowerBound 和 upperBound 这两个标准的二分的模板了。
此外,我们还需要记住这两个模板的使用的条件:
- lowerBound 用于查找有序数组中最左边出现的元素(闭)。
- upperBound 用于查找有序数组中最右边出现的元素(开)。
注意,我们在条件部分加了 “开闭” 两个字!其含义如下:
当给定数组 A[] = {1,2,2,2,3},运行 lowerBound(A, 2) 返回下标 1,而运行 upperBound(A,2) 却返回下标 4,但此时 A[4] = 3。
因此,我们还需要注意,lowerBound 与 upperBound 返回值组成的区间是一个左闭右开的区间,如下所示:
[lowerBound(A,2), upperBound(A,2)) = [1, 4)
一定要记住这里的左闭右开原则!
lowerBound
其中 lowerBound 的代码模板如下:
int lowerBound(long[] A, int n, long target) {int l = 0, r = n;while (l < r) {final int m = l + ((r - l) >> 1);if (A[m] < target) {l = m + 1;} else {r = m;}}return l;}
upperBound
upperBound 的模板代码如下:
int upperBound(long[] A, int n, long target) {int l = 0, r = n;while (l < r) {final int m = l + ((r - l) >> 1);if (A[m] <= target) {l = m + 1;} else {r = m;}}return l;}
其实我们只需要记忆 lowerBound 模板就够了,因为两个模板之间的差异只有一处:
lowerBound:A[m] < target
upperBound:A[m] <= target
这里和你分享一个我的记忆方法。当 A[m] <= target 的时候,标志着 m 还可以往右移动一段距离,因为 upperBound 找到的一般都在更右边的位置,因此带有 “A[m] <= target” 的是 upperBound。
双指针
双指针的知识我们总结如下:
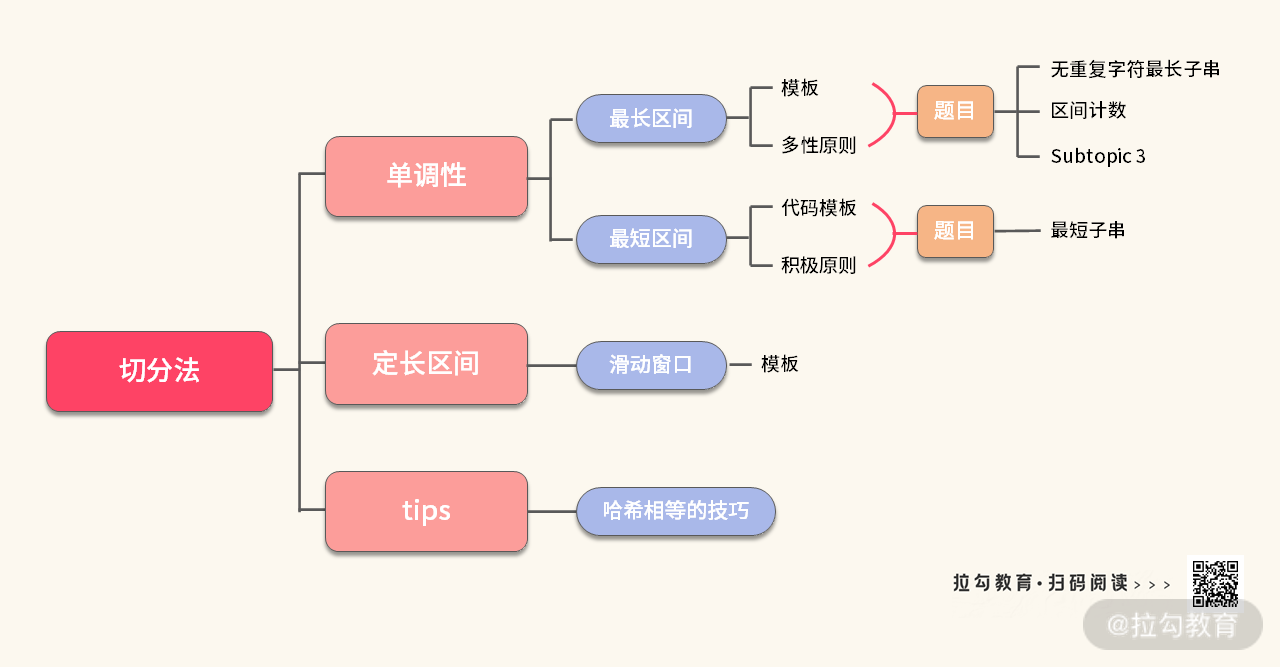
需要熟练掌握的代码模板,一共有 3 个。
最长区间
求最长区间的代码模板长成这样:
int maxLength(int[] A) {int N = A.length;int left = -1;int ans = 0;for (int i = 0; i < N; i++) {while (check((left, i]))) {++left;}ans = max(ans, i - left);}return ans;}
注意:在解题的时候,需要根据具体的题目条件,在模板的基础上写一点状态更新的代码,也就是要替换掉代码模板中的 “TODO” 部分。
定长区间
其实定长区间就是固定窗口大小的滑动窗口算法,这里我整理好了一个通用的模板,如下所示:
int fixedLength(int[] A, int windowSize) {final int N = A == null ? 0 : A.length;int left = -1;for (int i = 0; i < N; i++) {if (i - left < windowSize) {continue;}left++;}return ans;
注意:这个代码模板也是需要根据具体的题目条件完成 “TODO” 的部分。不同的题目,状态更新的代码可能会稍有不同。
最短区间
最短区间的代码模板如下:
int minimalRange(int[] A) {final int N = A == null ? 0 : A.length;int left = -1;int ans = A.length + 1;for (int i = 0; i < N; i++) {while (区间超出/满足条件) {ans = Math.min(ans, i - left);}}return ans;}
注意:状态更新的代码同样需要根据题目的条件完成 “TODO” 的部分。
贪心
虽然说贪心算法是一种思想,不过还是有一些代码模板需要你掌握。比如区间不重复的最大数目模板,如下所示:
int nonOverlapIntervals(int[][] A) {final int N = A == null ? 0 : A.length;Arrays.sort(A, new Comparator<int[]>() {public int compare(int[] a, int[] b) {return a[1] == b[1] ? 0 : (a[1] < b[1] ? -1 : 1);}});int maxEnd = Integer.MIN_VALUE;int ans = 0;for (int i = 0; i < N; i++) {final int start = A[i][0];if (maxEnd <= start) {maxEnd = A[i][1];ans++;}}return ans;}
此外,在《11 | 贪心:这种思想,没有模板,如何才能掌握它?》中我们介绍过 “青蛙跳” 问题, 实际上该解法还可以解决一系列题目,比如“第 11 讲” 的练习题 5,练习题 6 等。因此,我把这个算法模板叫作青蛙跳模板。
boolean canJump(int[] A) {final int N = A == null ? 0 : A.length;int preScanedPos = -1;int curCoveredRange = 0;while (curCoveredRange < N - 1) {int oldCoveredRange = curCoveredRange;for (int i = preScanedPos + 1; i <= oldCoveredRange; i++) {if (i + A[i] > curCoveredRange) {curCoveredRange = i + A[i];}}if (oldCoveredRange == curCoveredRange) {return false;}preScanedPos = oldCoveredRange;}return true;}
回溯
关于回溯,我经常从两个方向思考:
- 只看第 i 个人怎么选;
- “有借有还”。
关于这两点,希望你看了下面的这个思维导图还能够想起来。
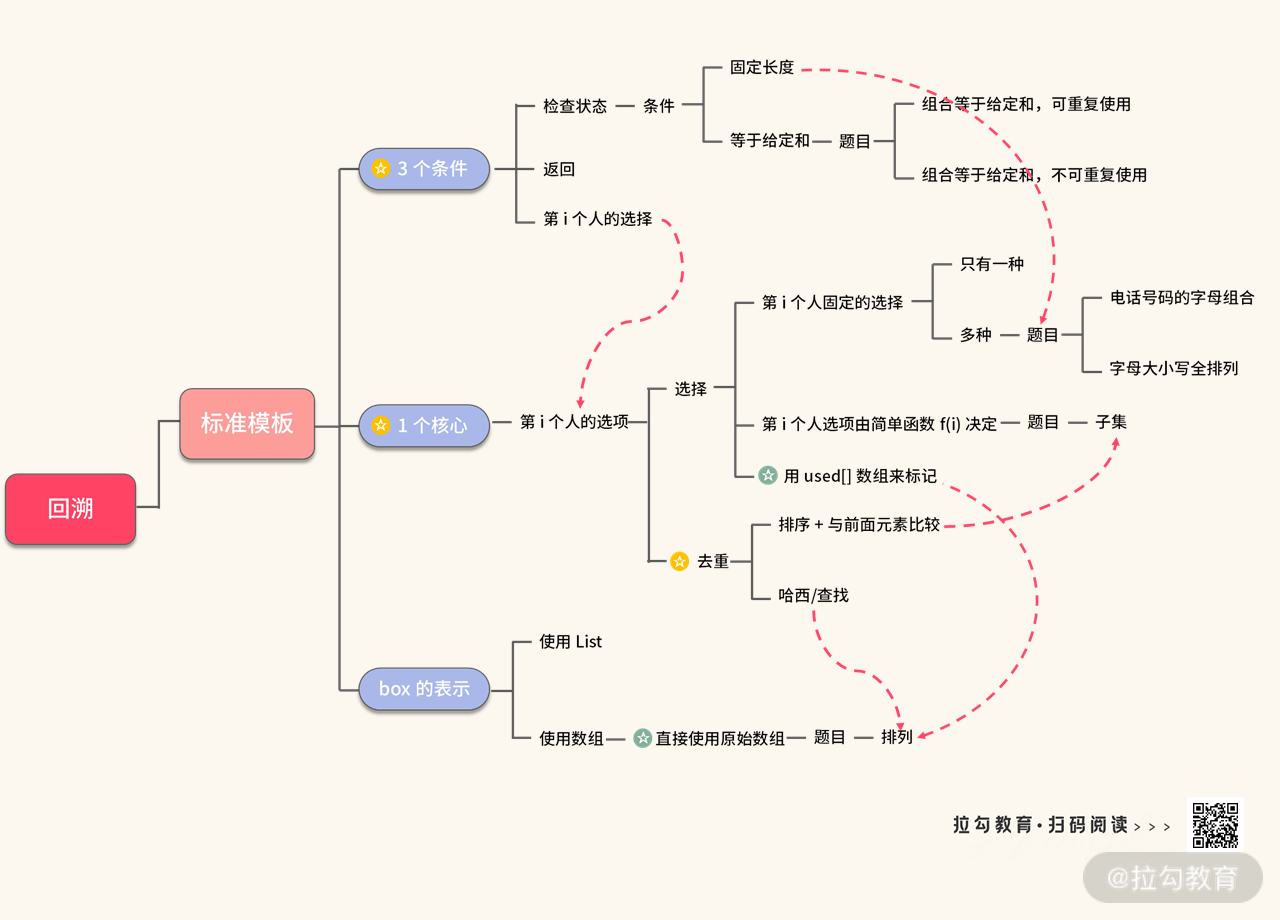
回溯的代码模板只有一个,如下所示:
void backtrace(int[] A,int i,Box s,answer) {final int N = A == null ? 0 : A.length;if (状态满足要求) {answer.add(s);}if ([i, ...., 后面)的人都没有任何选项了) {return;}for 宝石 in {第i个人当前所有宝石选项} {s.push(宝石);backtrace(A, i + 1, s, answer);s.pop();}}
DFS 与 BFS
DFS 与 BFS 的知识点我压缩在了一张思维导图里:
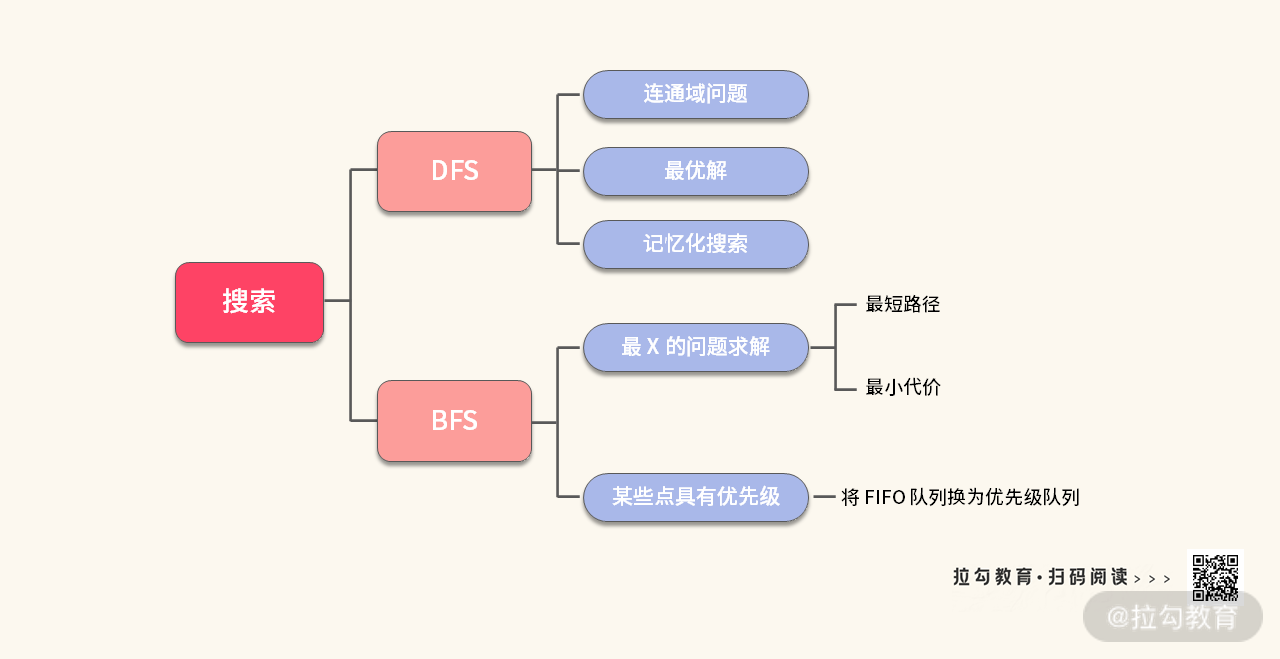
关于代码模板,你只需要掌握两个。
DFS
通常而言,DFS 算法会用到两个模板,一个用于遍历,另一个用于收集符合条件的解。其中用于遍历的代码模板如下:
boolean vis[N];void DFS(int start) {if start == end {success = truereturn}for opt in getOptions(start) {if (vis[opt]) continue;vis[opt] = true;dfs(opt);if success {return;}}}
用于收集符合条件的解的代码模板如下:
void dfs(A,int start,vis,path,answer) {final int N = A == null ? 0 : A.length;if (状态满足要求) {if (s better_than ans) {ans = s}return;}for next in {start点的后继点} {if !vis[next] {path.append(next);vis[next] = true;dfs(A, next, vis, path, answer);path.pop();vis[next] = false;}}}
BFS
巧合的是,BFS 也有两种写法,一种是使用队列,另一种是使用 “两段击”。其中使用队列的代码写法如下:
bfs(s) {q = new queue()q.push(s), visited[s] = truewhile (!q.empty()) {u = q.pop()for next in getNext(u) {if (!visited[next]) {q.push(next)visited[next] = true}}}}
使用 “两段击” 的代码写法如下:
bfs(s) {cur = {s};visited[s] = true;while (!cur.empty()) {next = [];for c in cur {for next in getNext(c) {if (!visited[next]) {next.append(next);visited[next] = true;}}}cur = next;}}
动态规划
动态规划其实并没有太多的模板可以套,你需要通过实战练习不停地提高自己的应对能力。掌握动态规划的重点在于 6 步分析法,如下图所示:
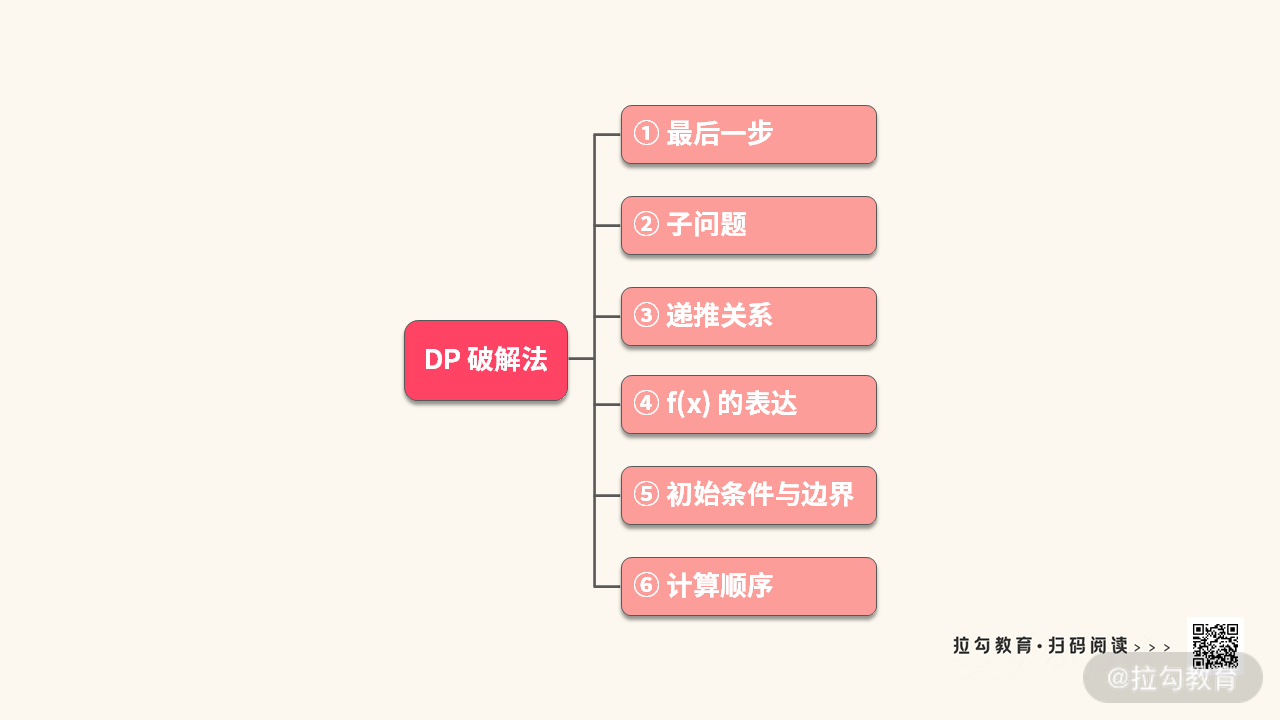
这里我们重点看一下需要你熟练掌握的 KMP 算法模板(你还记得求 next 数组时的动态规划吗?),如下所示:
int[] buildNext(String sub) {final int N = sub == null ? 0 : sub.length();int[] next = new int[N + 1];int i = 0;int j = -1;next[0] = -1;while (i < N) {if (j == -1 || sub.charAt(i) == sub.charAt(j)) {i++;j++;if (i < sub.length() && j < sub.length() &&sub.charAt(i) == sub.charAt(j)) {next[i] = next[j];} else {next[i] = j;}} else {j = next[j];}}return next;}int KMP(String main, String sub) {int i = 0;int j = 0;final int alen = main.length();final int blen = sub.length();int[] next = buildNext(sub);while (i < alen && j < blen) {if (-1 == j || main.charAt(i) == sub.charAt(j)) {i++;j++;} else {j = next[j];}}return j == blen ? i - blen : -1;}
总结
整理好算法的代码模板之后,最后我再强调一点,也是新手往往容易犯错的地方。
不要试图把刷过的所有题都放到代码模板中,因为你复习的时候容易没有重点。另外,人的记忆能力是有限的,如果你强记一段代码,可能效果并不好。更重要的是勤于将知识进行整理、归纳以及压缩。然后将它们打包成知识库中的 “积木”,在需要的时候直接拿来用,而不是再从 0 到 1 推导。
算法模板就整理到这里了,接下来,我将和你聊聊我的大厂面试经历,谈谈我对算法学习的看法,让我们继续前进。

