数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
今天我会带你深度思考子集,介绍掌握 5 种通用解法。
不知道你对子集问题是否还有印象,我们曾在 “12 | 回溯:我把回溯总结成一个公式,回溯题一出就用它”,花了大量篇幅深入讨论过子集相关的问题。但当时的思路是已经知道了解题方法,然后再对题目实施 “精确制导的定向爆破”。
但是,子集问题的解法就只有回溯吗?我们是否还可以继续深挖题目给予的信息?在这个 “一题多解” 的模块里面,我们需要重新审视子集问题,比如看一看:
- 能否挖掘出更多的信息?
- 能不能匹配到更多的算法和数据结构?
- 能不能找到更多有趣的解法。
下面请你带着以上三个问题,开启今天的探索旅程。
题目
首先,子集问题实际上包含两类问题。下面我们通过两个题目详细介绍一下。
【题目 1】给你一个整数数组 nums ,数组中的元素互不相同。返回该数组所有可能的子集。
解集不能包含重复的子集。你可以按任意顺序返回解集。
示例 1
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
【题目 2】给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集。解集不能包含重复的子集。返回的解集中,子集可以按任意顺序排列。
示例 1
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
注:在后文中,我们将分别用题目 1、题目 2 来引用这两个题目。
声明:对于这个题目,在最差情况下,时间复杂度都是 O(N2N)。不算返回值的情况下,空间复杂度为 O(N)(BFS 的空间复杂度会到 O(2N))。因此,后面的代码不会再对时间复杂度和空间复杂度做特别的声明。
通用方法 1:回溯
首先,因为题目中已经说明了,数组中的每个元素都是不相同的,因此题目 1 不涉及去重。我们在 “第 12 讲”中利用 “回溯法:一个核心,三个条件” 写过题目 1 的回溯代码。关于这种方法,不再做过多的叙述,你可以参考如下代码(解析在注释里):
void append(List<Integer> box, List<List<Integer>> all) {all.add(new ArrayList<>());for (Integer x : box) {all.get(all.size() - 1).add(x);}}void backTrace(int[] A,int start,List<Integer> box,List<List<Integer>> all) {final int N = A == null ? 0 : A.length;append(box, all);if (start >= N) {return;}for (int j = start; j < N; j++) {box.add(A[j]);backTrace(A, j + 1, box, all);box.remove(box.size() - 1);}}public List<List<Integer>> subsets(int[] A) {final int N = A == null ? 0 : A.length;List<Integer> box = new ArrayList<>();List<List<Integer>> ans = new ArrayList<>();backTrace(A, 0, box, ans);return ans;
可以看到,题目 2 与题目 1 有一点不同:
题目 2 给定的数组可能存在重复元素,因此,还需要对子集进行去重。
接下来我们讨论题目 2 中涉及的去重问题。
当时,我们采用 “排序 + 判断元素是否出现过” 的方法进行去重。经过优化后的代码如下(解析在注释里):
class Solution {private void append(List<Integer> box,List<List<Integer>> ans) {ans.add(new ArrayList<>());for (Integer x : box) {ans.get(ans.size() - 1).add(x);}}private void backtrace(int[] A,int start,List<Integer> box,List<List<Integer>> ans){final int N = A == null ? 0 : A.length;append(box, ans);if (start >= N) {return;}for (int j = start; j < N; j++) {if (j > start && A[j] == A[j-1]) continue;box.add(A[j]);backtrace(A, j + 1, box, ans);box.remove(box.size()-1);}}public List<List<Integer>> subsetsWithDup(int[] A) {final int N = A == null ? 0 : A.length;List<Integer> box = new ArrayList<>();List<List<Integer>> ans = new ArrayList<>();if (N <= 0) {return ans;}Arrays.sort(A);backtrace(A, 0, box, ans);return ans;}}
其实,这是一道非常经典的题目,我们可以从不同角度思考这个题目,进而得到不同的解法。
通用方法 2:BFS
既然可以利用回溯(可以认为回溯是某种形式的 DFS),那么应该也可以尝试往 BFS 方向思考。因为大部分时候,DFS 的代码都可以改写为 BFS 的代码,
题目 1 不需要考虑去重的问题。我们可以假设数组为 A[] = {1, 2, 3},那么可以进行如下的操作(解析在注释里):
cur = {{}};for x in A:tmp = {};for subset in cur:subset.add(x)tmp.add(subset)for subset in tmp:cur.add(subset)return cur
不过,我们也要注意到,这里在进行 BFS 的时候,与常规的 BFS 不太一样。
BFS 的方法有两种,一种是使用 Queue,另一种是使用 “两段击”。这里我们指的是两段击。
如果你忘了什么是 “两段击”,那么快去看一下 “02 | 队列:FIFO 队列与单调队列的深挖与扩展”。
常规的 BFS 流程如下(我们聚焦于 BFS 的一轮迭代):
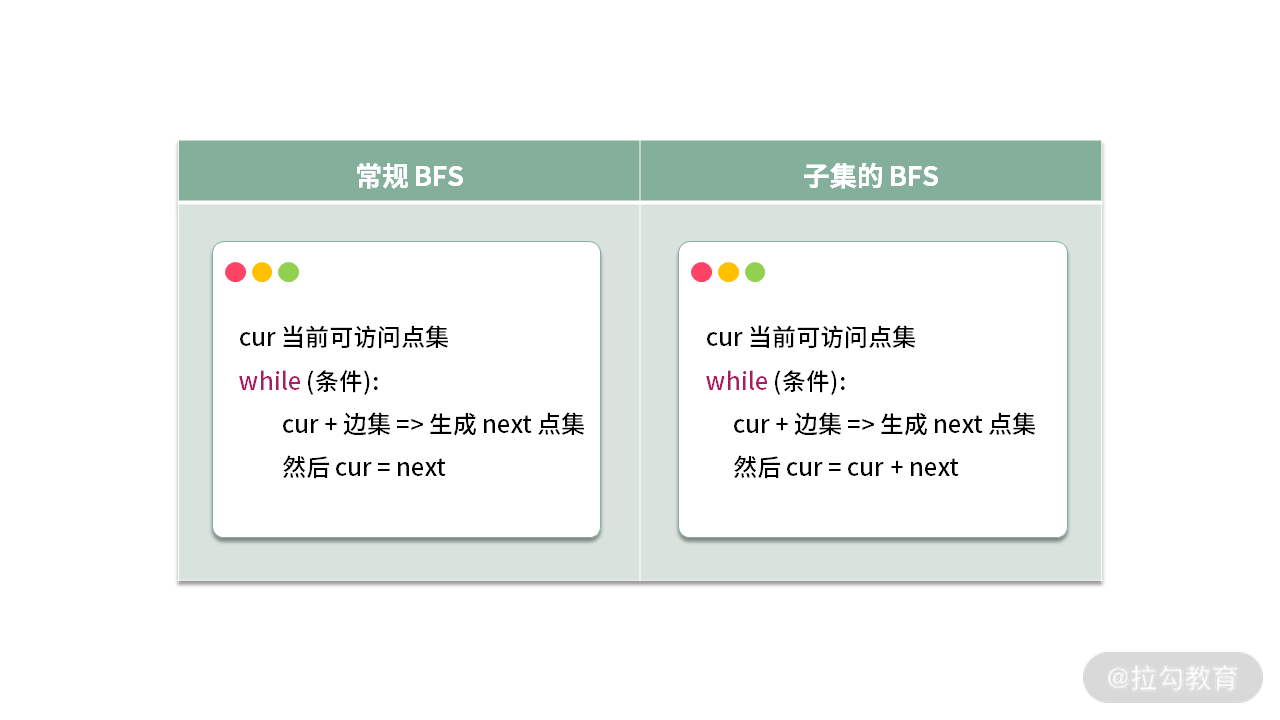
我们发现,进行 BFS 的时候,在生成 next 之后,并不是直接赋值给 cur,而是采用了 cur + next。这里我建议你花点时间完成下面两道常规 BFS 的练习题,巩固一下 BFS 的知识。
练习题 1:从上到下按层打印二叉树,同一层结点按照从左到右的顺序打印,每一层打印到一行。
练习题 2:有 n 个城市通过 m 个航班连接。每个航班都从城市 u 开始,以价格 w 抵达 v。现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到从 src 到 dst 最多经过 k 站中转的最便宜的价格。 如果没有这样的路线,则输出 -1。
输入:n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 1
输出:200
城市航班图如下:
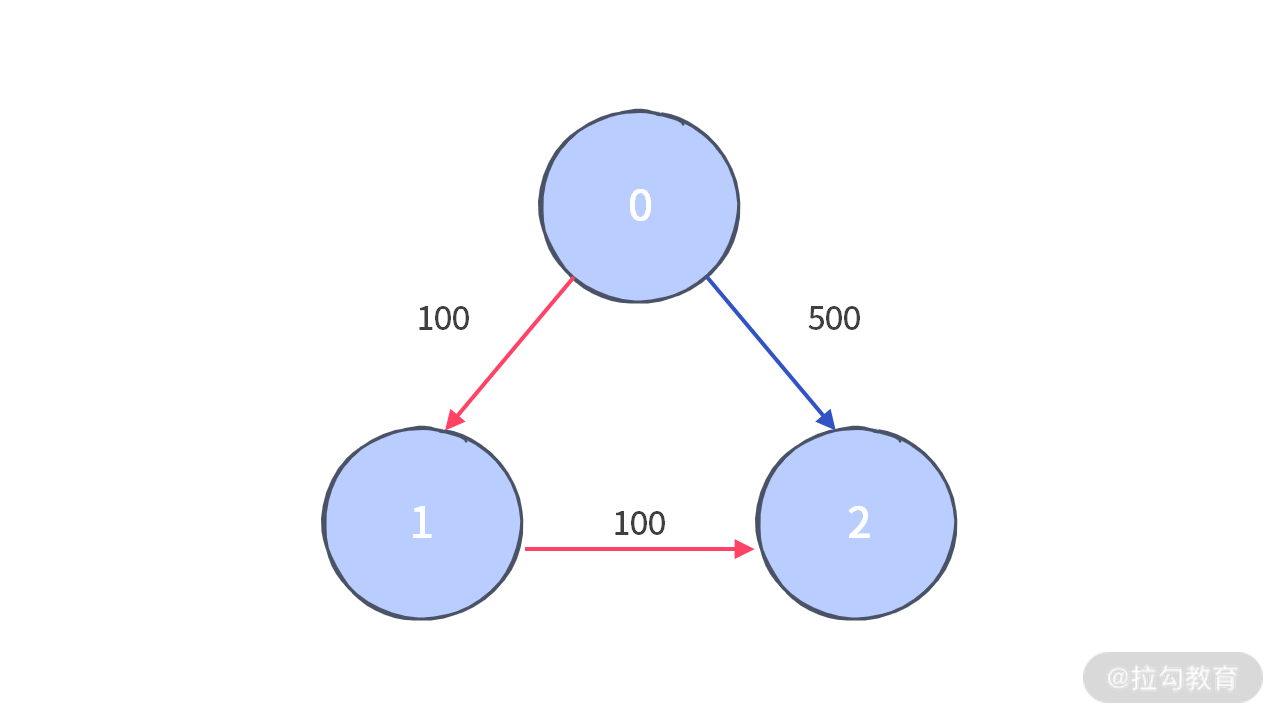
从城市 0 到城市 2 在 1 站中转的最便宜价格是 200,如上图中红色所示:
既然我们已经知道子集的 BFS 的程序框架了,针对题目 1,可以写出代码如下(解析在注释里):
class Solution {public List<List<Integer>> subsets(int[] nums) {List<List<Integer>> cur = new ArrayList<>();cur.add(new ArrayList<>());List<List<Integer>> next = new ArrayList<>();for (int x: nums) {next.clear();for (List<Integer> subset: cur) {List<Integer> newSubset = new ArrayList<>(subset);newSubset.add(x);next.add(newSubset);}for (List<Integer> newSubset: next) {cur.add(newSubset);}}return cur;}}
当题目 1解决之后,我们再来看一下能不能用同样的 BFS 方法解决题目 2。假设 A[] = {1,2,2}。看看是否会出现什么问题,步骤如下:
Step 1. 一开始 cur = [{}];
Step 2. 当加入元素 1,生成 next = [{1}];
Step 3. cur = cur + next = [{}, {1}];
Step 4. 再加入元素 2,生成 next = [{2}, {1,2}];
Step 5. cur = cur + next = [{}, {1}, {2}, {1,2}];
Step 6. 再加入元素 2,生成 next = [{2}, {1,2}, {2,2}, {1,2,2}];
Step 7. 最后执行 cur = cur + next = [{}, {1}, {2}, {1,2},{2}, {1,2}, {2,2}, {1,2,2}]。
我们发现,如果还是沿用题目 1 的 BFS 方法,会在最终解中产生重复的子集。那么,有没有办法去除这些重复的子集?
下面我们需要追踪一下这些重复元素是如何生成的,可以画出下图:
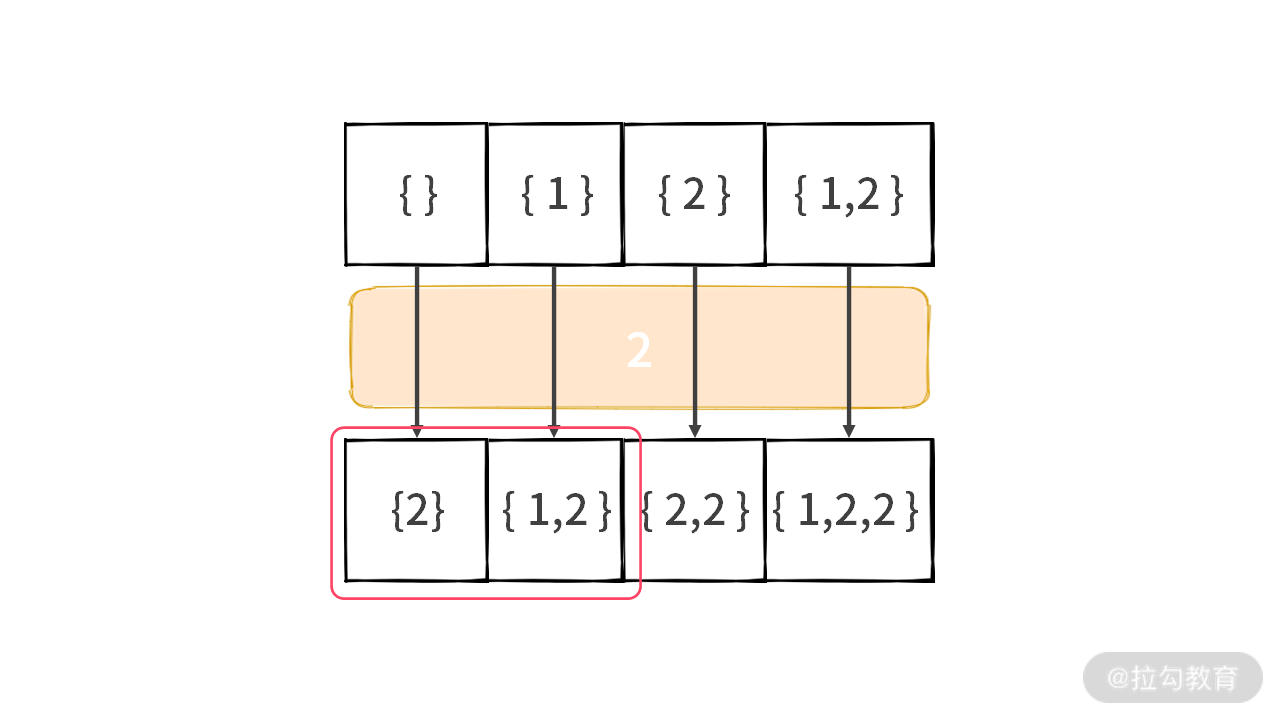
重复元素 [{2}, {1,2}] 是由 [{}, {1}] 加入元素 2 后生成的。重复的元素分别是在 Step 4 和 Step 6 生成的,如下图所示:
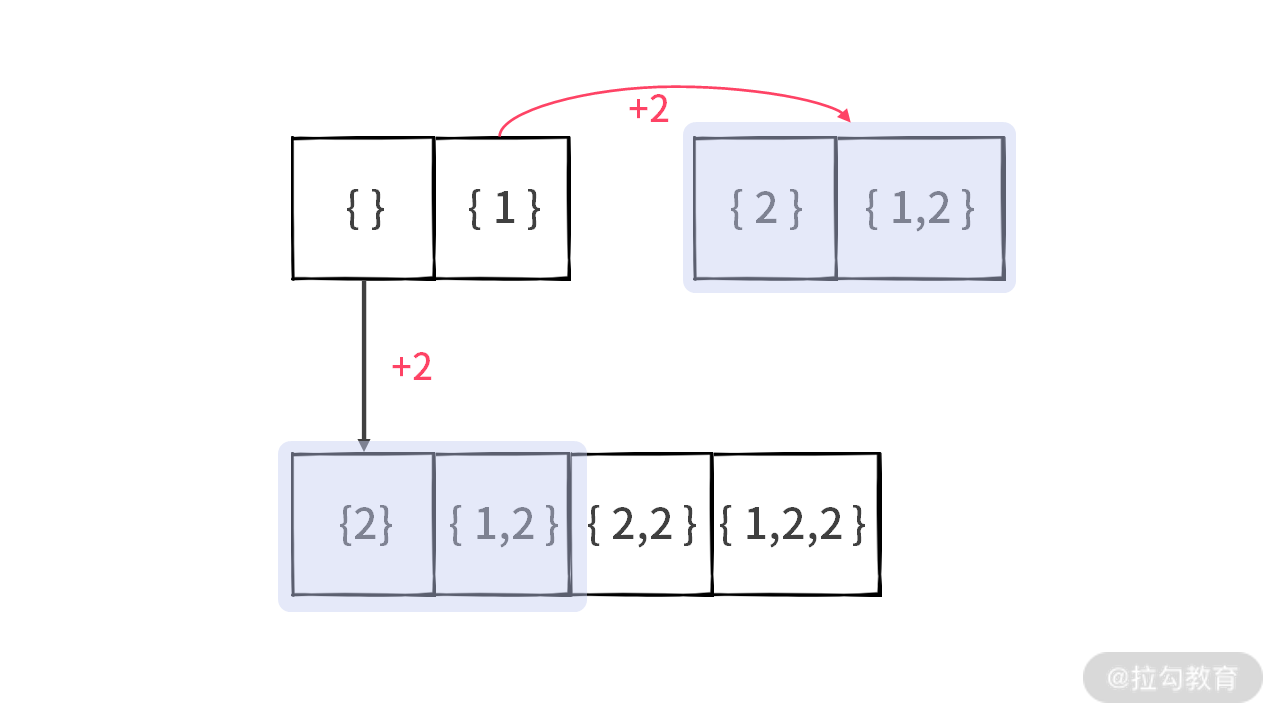
因此,在更新的时候,应该要注意,如果一些元素,比如 [{}, {1}] 已经被元素 2 更新过了。那么后面就不应该再去更新了。
此时,我们应该可以写出伪代码了:
cur = [{}]for x in A:next = []for subset in cur:if updated(subset, x) == False:next.add(subset.clone().add(x))for newSubset in next:cur.add(newSubset)return cur
现在问题的重点在于:如何完成 updated(subset, x) 的检查。我们发现可以按照下图这样的方式操作:
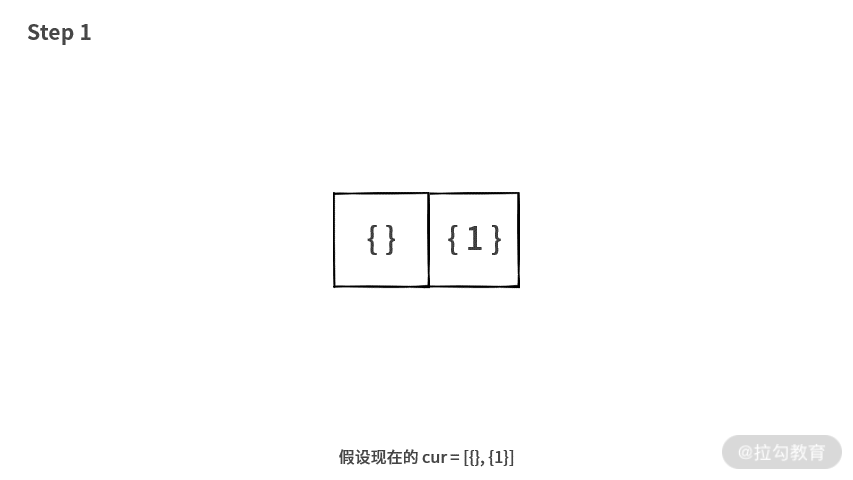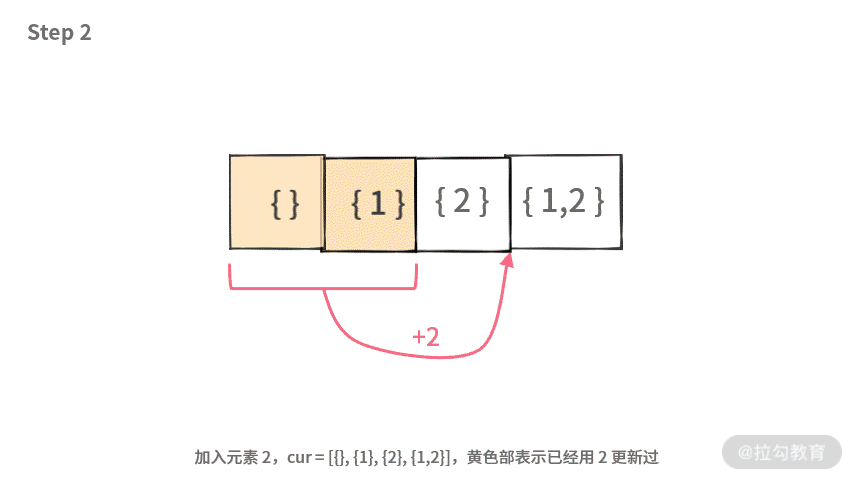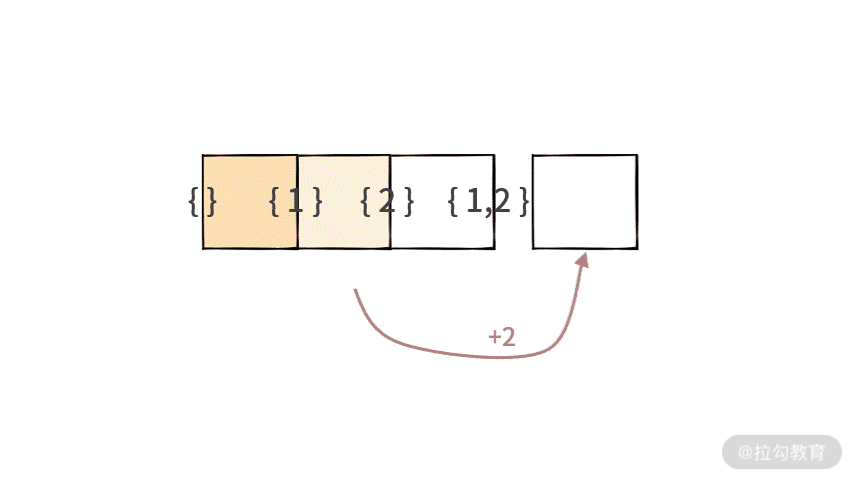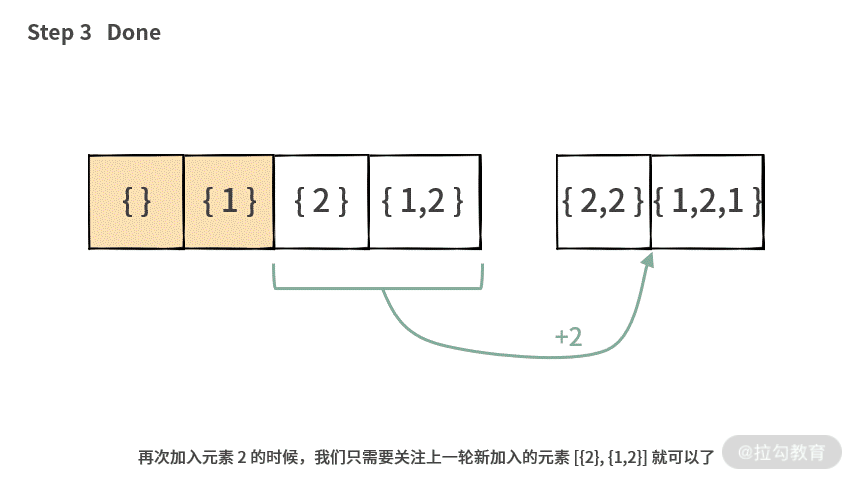
通过上述分析, 我们可以总结出如下结论:
- 如果加入的元素与前面加入的元素一样,那么只需要更新 “新增的部分”;
- 为了同时达到,就需要与前面一轮的元素进行比较,并且记住前面新增的部分。
也就是说,我们需要做两个事情:
- 对数组排序,排序之后,我们总是可以很容易得出与前面一轮的元素是否相等;
- 记住前面新增的部分,我们只需要每次更新之前,记录一下 cur 的 size 就可以了。
基于这两点,可以写出题目 2 的代码如下(解析在注释里):
class Solution {public List<List<Integer>> subsetsWithDup(int[] nums) {Arrays.sort(nums);List<List<Integer>> cur = new ArrayList<>();cur.add(new ArrayList<>());List<List<Integer>> next = new ArrayList<>();int pre = Integer.MAX_VALUE;int beforePreUpdateSize = 0;for (int curValue: nums) {next.clear();int startUpdatePos = 0;if (curValue == pre) {startUpdatePos = beforePreUpdateSize;}for (int i = startUpdatePos; i < cur.size(); i++) {List<Integer> newSubset = new ArrayList<>(cur.get(i));newSubset.add(curValue);next.add(newSubset);}int beforeCurValueUpdateSize = cur.size();for (List<Integer> subset: next) {cur.add(subset);}beforePreUpdateSize = beforeCurValueUpdateSize;pre = curValue;}return cur;}}
【小结】我们不妨将用到的 BFS 进行比较,通过比较它们之间的异同,有助于梳理知识点里面的考点(红色部分是变更之后的考点)。
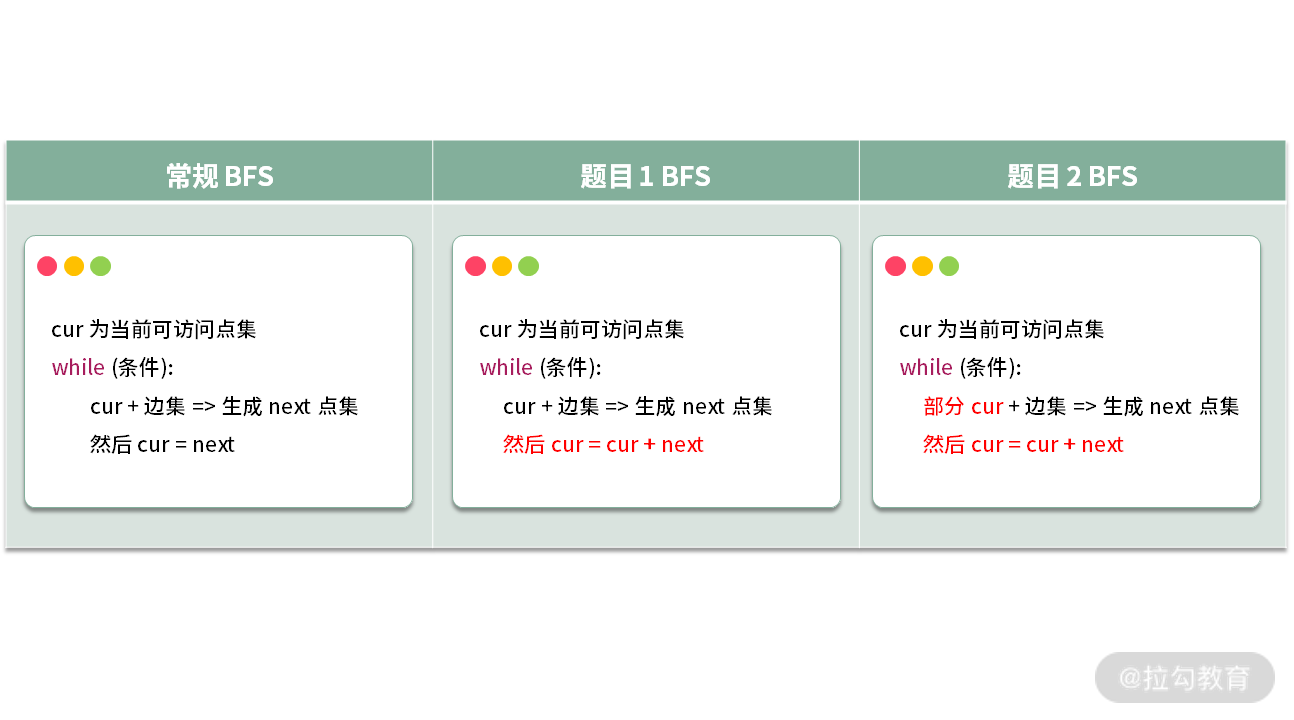
我们发现,题目 1 与题目 2 无非就是在原始的 BFS 上不停地更改 BFS 的条件,然后就出现了新的题型与考点。
这里我再给你留一个练习题,通过这些练习,可以和我们以前学习过的知识产生联动,让你对题目、知识点的理解更加深刻。
练习题 3:在学习 “第 12 讲” 回溯中例 4 的时候,也讲到了题目 2。在那里,我们同样用到了去重的技巧,并且也用到了排序。那么请问,“第 12 讲” 中用到的排序和这里 BFS 的排序的目的有什么异同点?
练习题 4:题目 2 在进行 BFS 的时候,采用了使用部分 cur 里面的元素来进行更新,并且生成 next 的办法。我们在讲解 “11 | 贪心:这种思想,没有模板,如何才能掌握它?”贪心算法例 3“青蛙跳”的时候,曾说过可以采用类似 BFS 的方法进行思考。那么题目 2 和 “青蛙跳” 有什么异同呢?
通用方法 3:选与不选
现在我们换一种思路来看这个题目:生成一个子集的时候,对于一个元素而言,就只有选与不选两种选择。如果用二进制 bit,0 表示选中,1 表示没有选中。
那么对于一个有 n 个元素的数组,可以用一个二进制串表示一个子集。比如空集就是所有的二进制 bit 都是 0。
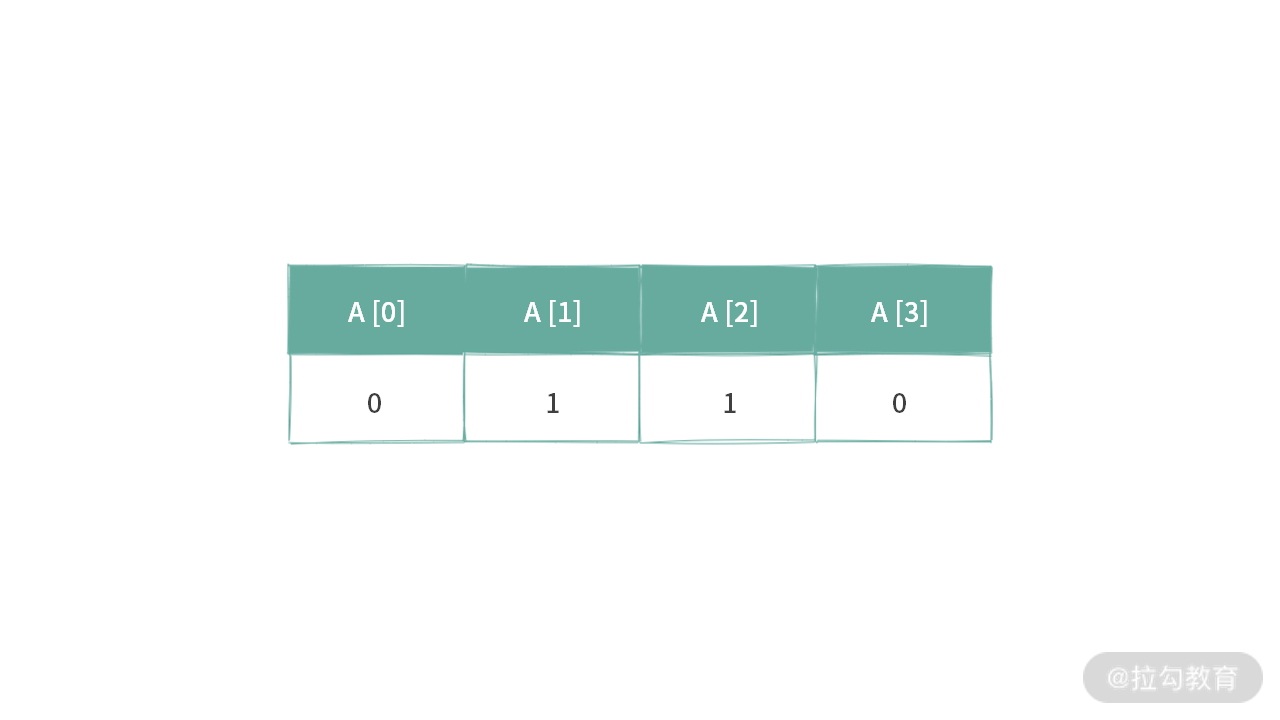
比如,我们还可以用 b0110 表示子集 {A[1], A[2]}。那么现在你应该明白,针对四个元素的子集,可以按照 [0, ~ b1111] 顺序遍历,然后依次遍历二进制串的每一位,通过 bit 0/1 决定是否需要把相应的元素放到集合中。
通过这种思路,我们可以写出题目 1的代码如下(解析在注释里):
class Solution {public List<List<Integer>> subsets(int[] nums) {final int N = nums == null ? 0 : nums.length;List<List<Integer>> ans = new ArrayList<>();for (int i = 0; i < (1<<N); i++) {List<Integer> subset = new ArrayList<>();for (int j = 0; j < N; j++) {final int mask = 1 << j;if ((i & mask) != 0) {subset.add(nums[j]);}}ans.add(subset);}return ans;}}
学完这种解法之后,我们会发现和 “14 | DP:我是怎么治好‘DP 头痛症’的?” 里面的状态压缩有非常类似的地方:
- 都是用 0/1 bit 位来表示一个元素的选中和不选中;
- 都是用一个整数来表示一个集合的状态。
题目 1 解决之后,我们接下来看一下题目 2。如果仍然采用这种方法,可能会面临一个问题。对于给定数组 A[] = {1,2,2,2}。如下图所示:
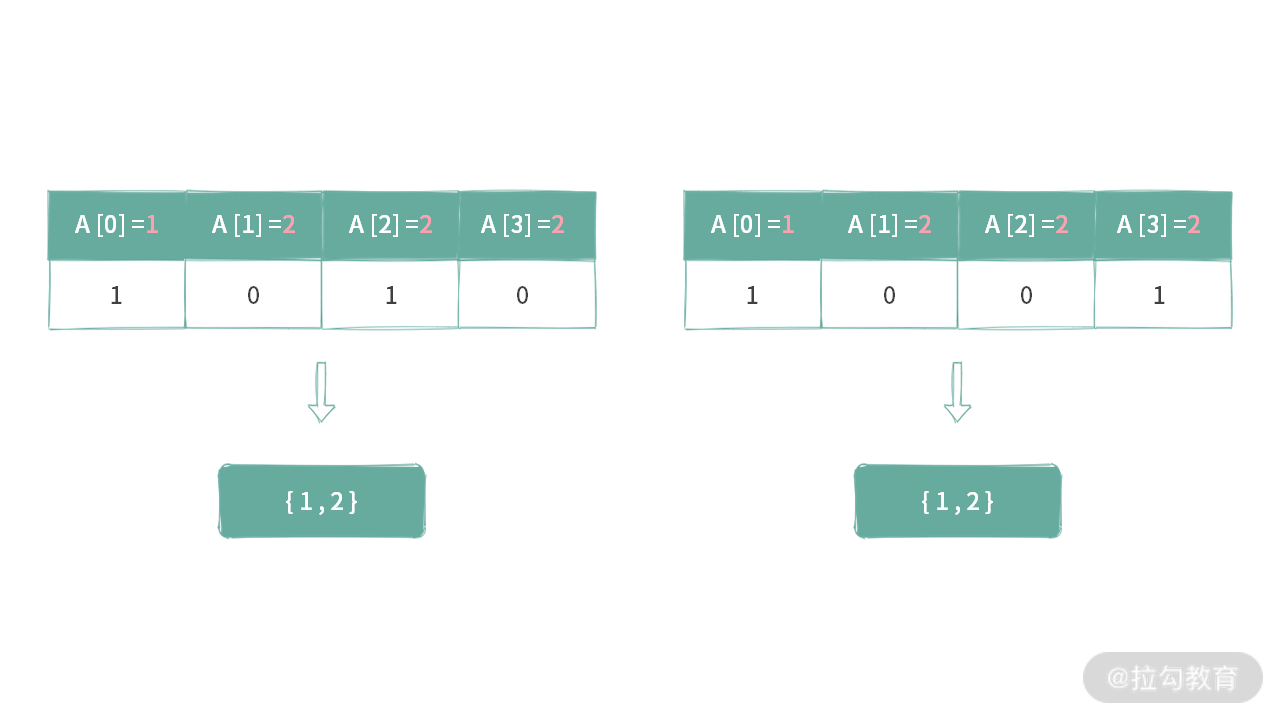
虽然用了两个不同的二进制串,但是会导致它们映射到同样的子集。因此,也就存在重复的可能性。那么,有没有什么办法可以去重呢?
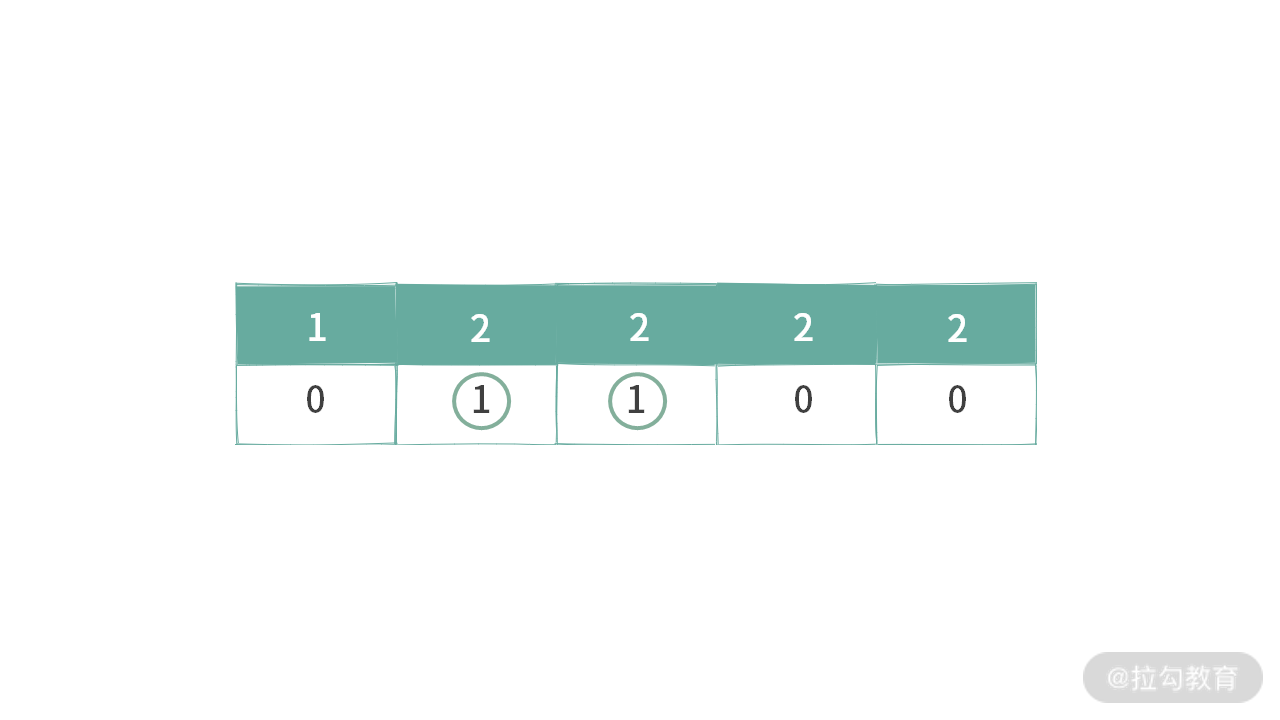
我们接着来看下面这个例子。对于数组 A[] = {1,2,2,2,2},可以发现有些二进制串实际上是等价的。比如只选中一个 1 的时候,如下图所示:
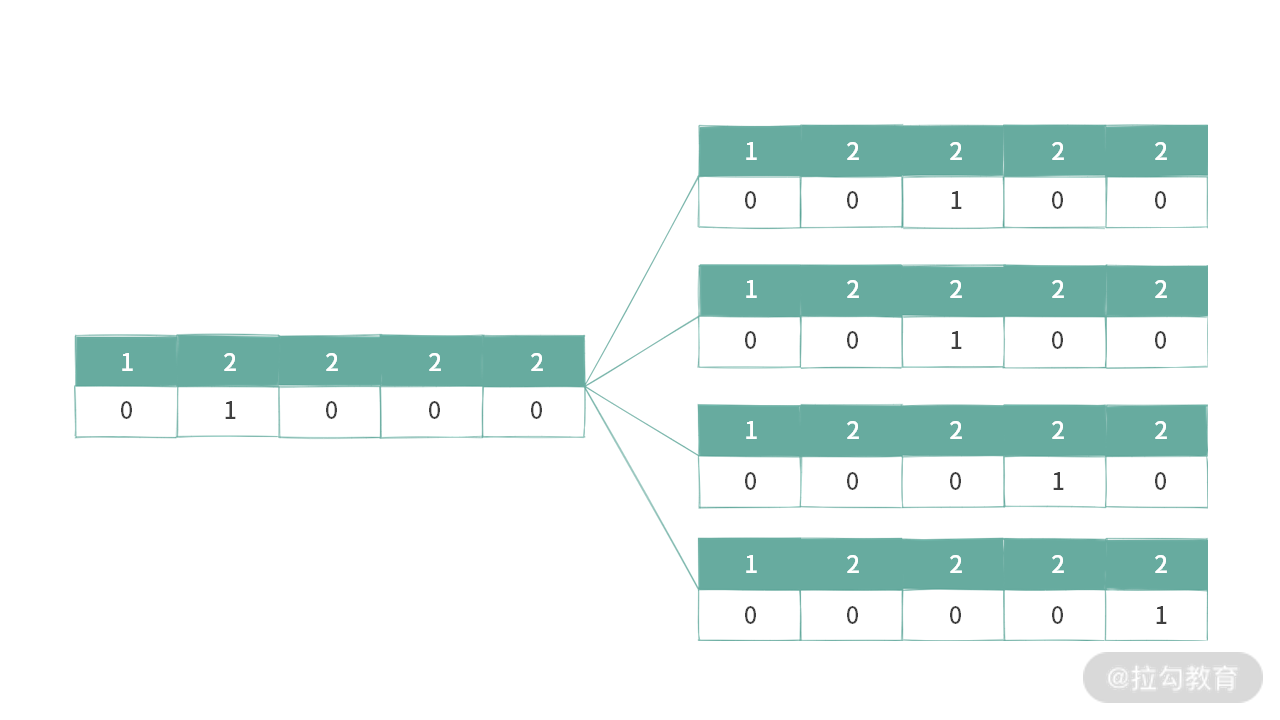
例 2:只选择 2 个 2 到子集里面的时候。如下图所示:
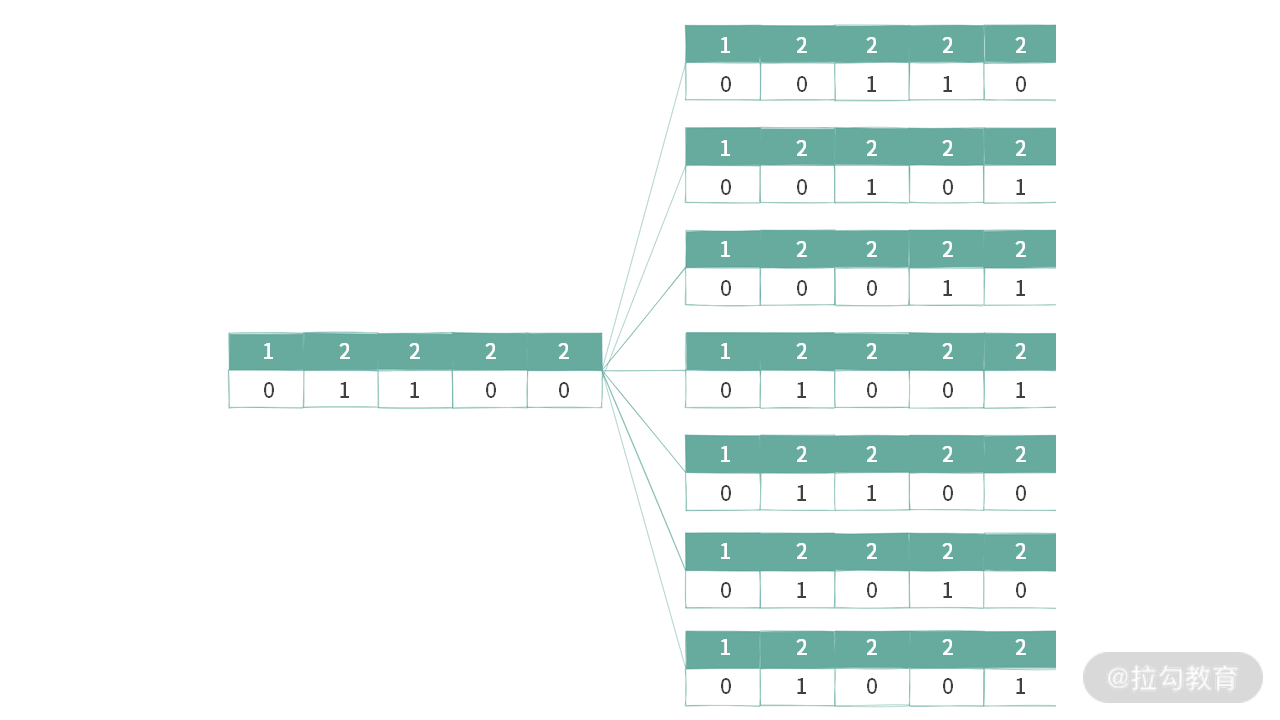
假设需要选择 x 个 2 出来,只需要数字 2 对应的位置 bit = 1 的总数有 x 个就可以了。比如,以选择 2 个 2 为例,只需 2 对应的位置有 2 个 bit=1 就可以了。
那么,在这些二进制串中,需要选择一个我们想要的数字出来。所以,现在问题的重点,就是选谁。
经过一系列挑选,我们精心按照一定规则,即相同的数的 bit = 1,挑选了如下数组的所有二进制串:
也就是说,本质上我们是在具有重复含义的二进制串中选出了 “代表”。比如下面这两个二进制串:
两个二进制串都表示往集合中添加:
- 1 个 1
- 2 个 3
- 2 个 4
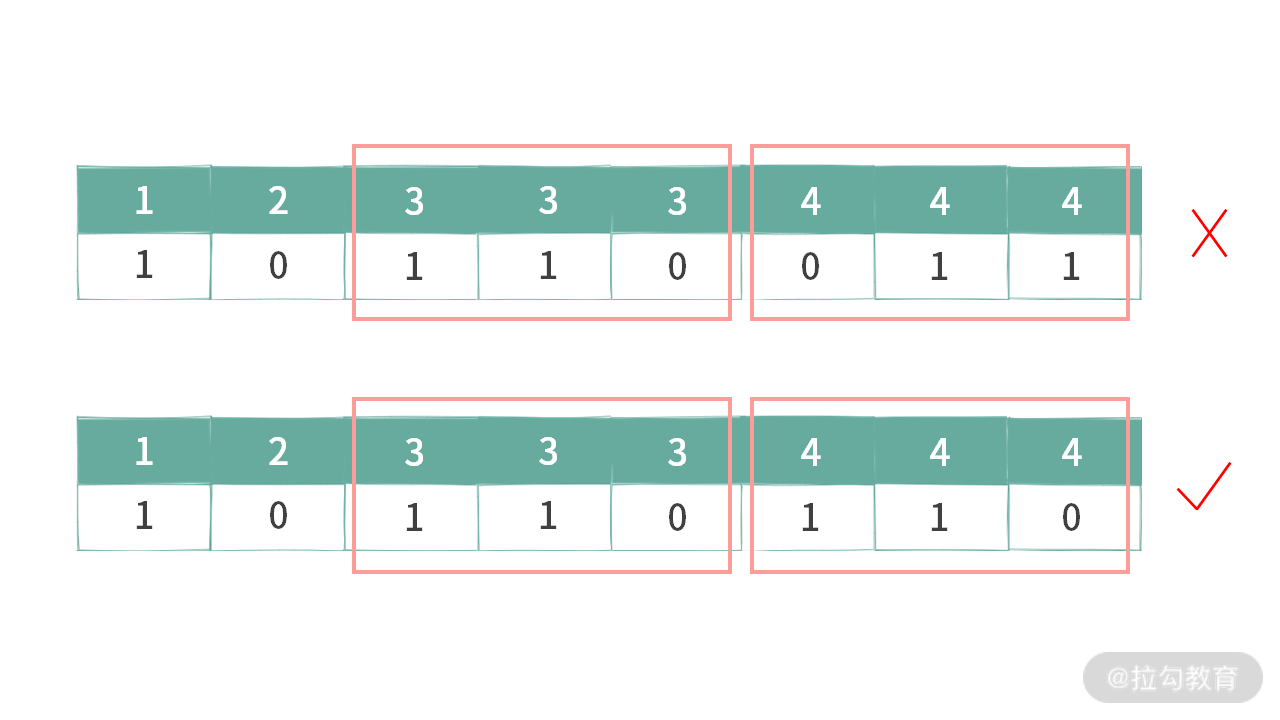
你可以观察上图中红色勾选的二进制串,上述选择规则有 2 个条件。注意,这里的条件都是针对数组中值相同的元素:
- 对于数组中的相同的元素,选中的时候,bit 为 1 时,都必须连在一起;
- 对于数组中的相同的元素,bit 为 1 时,都必须靠左边连续存放。
注意:这里的 “靠左存放” 不是靠整个二进制串的左边,而是靠着相同元素的左边界存放。如下图所示:
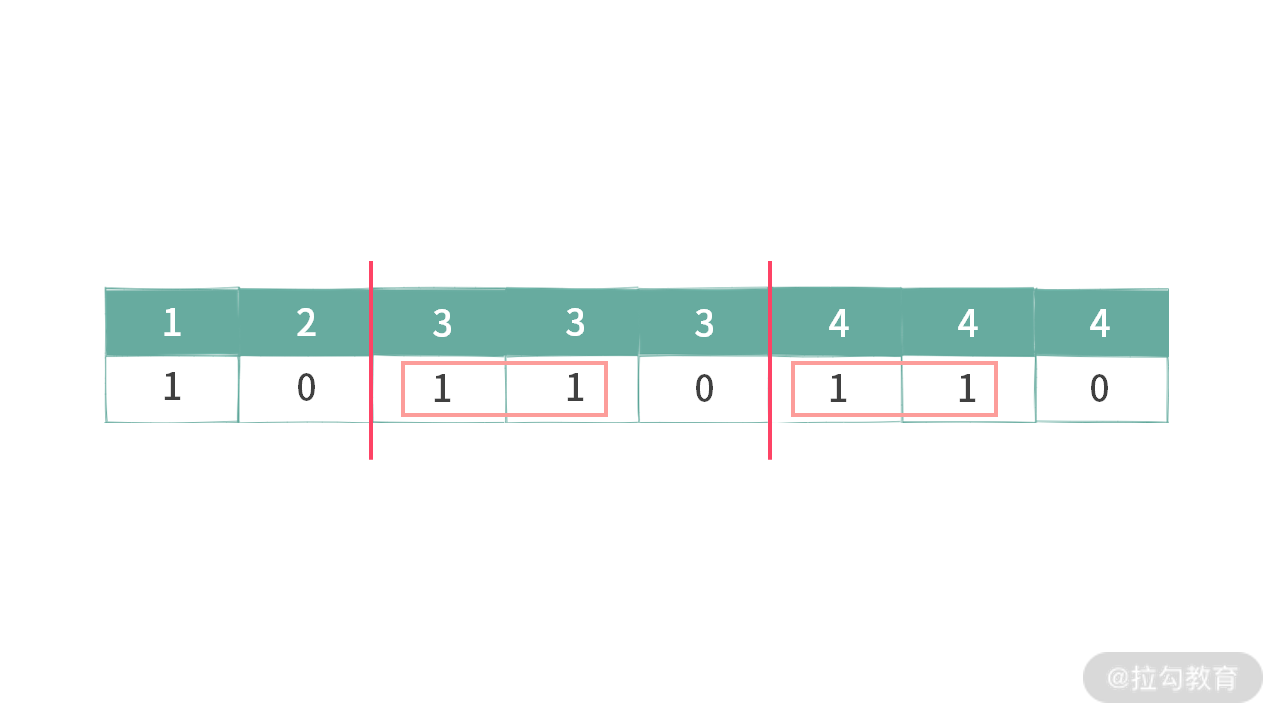
我们认为上图中相同元素 3 和元素 4 的 bit = 1 都是靠其左边连续存放的。
这里我给出一些示例,如下图所示:
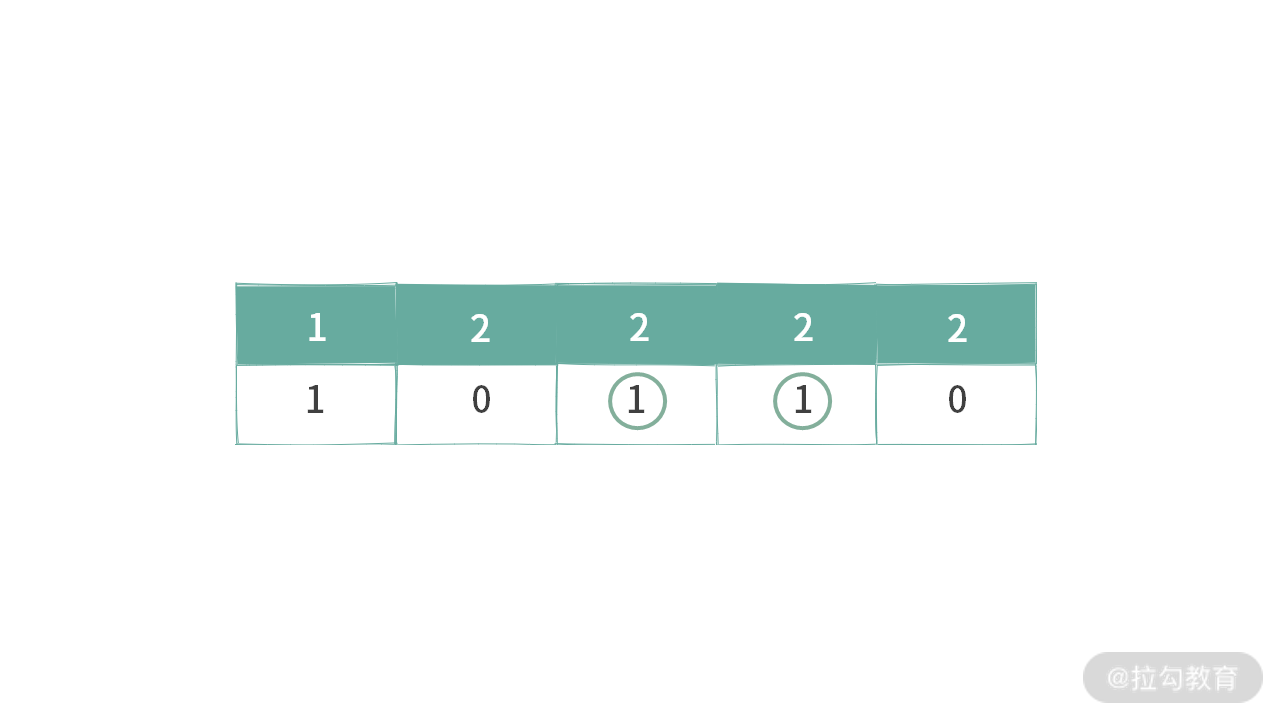
例 1,满足条件 1,不满足条件 2。因为选中元素 2 的 bit = 1 没有连续靠左存放。
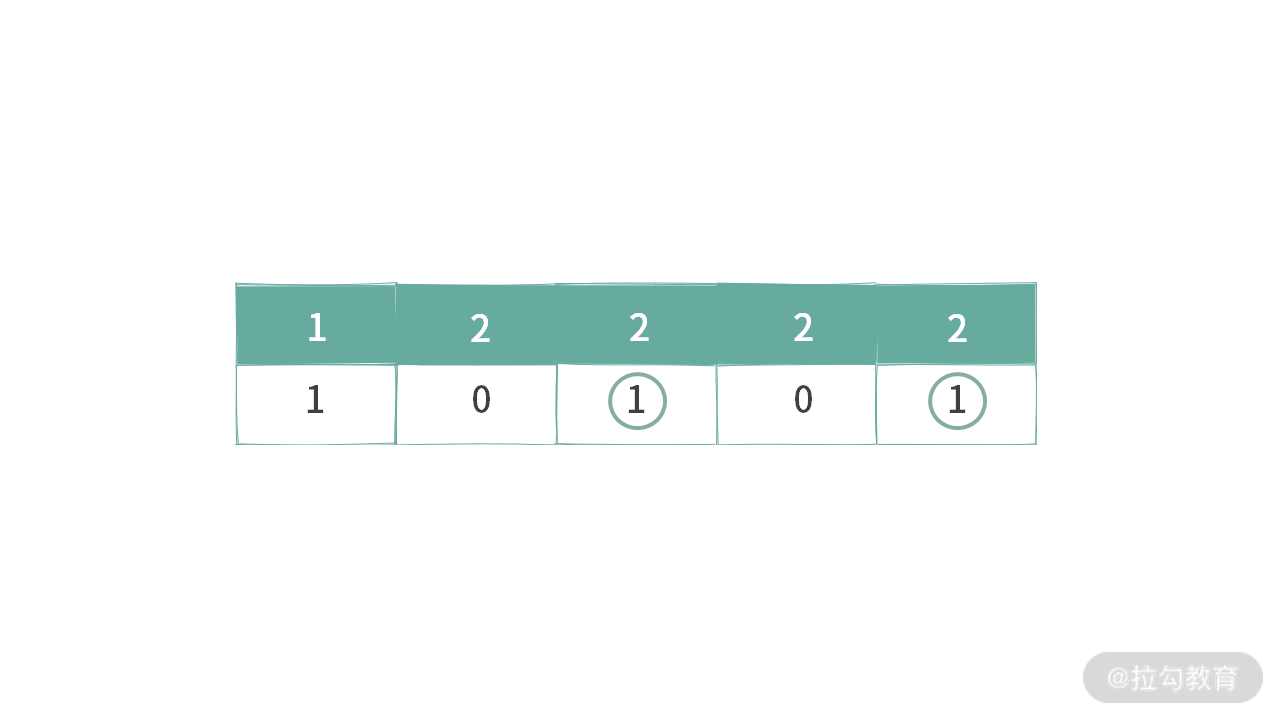
例 2,不满足条件 1,也不满足条件 2,因为选中相同元素的 bit = 1 没有连续,也没有靠左存放。
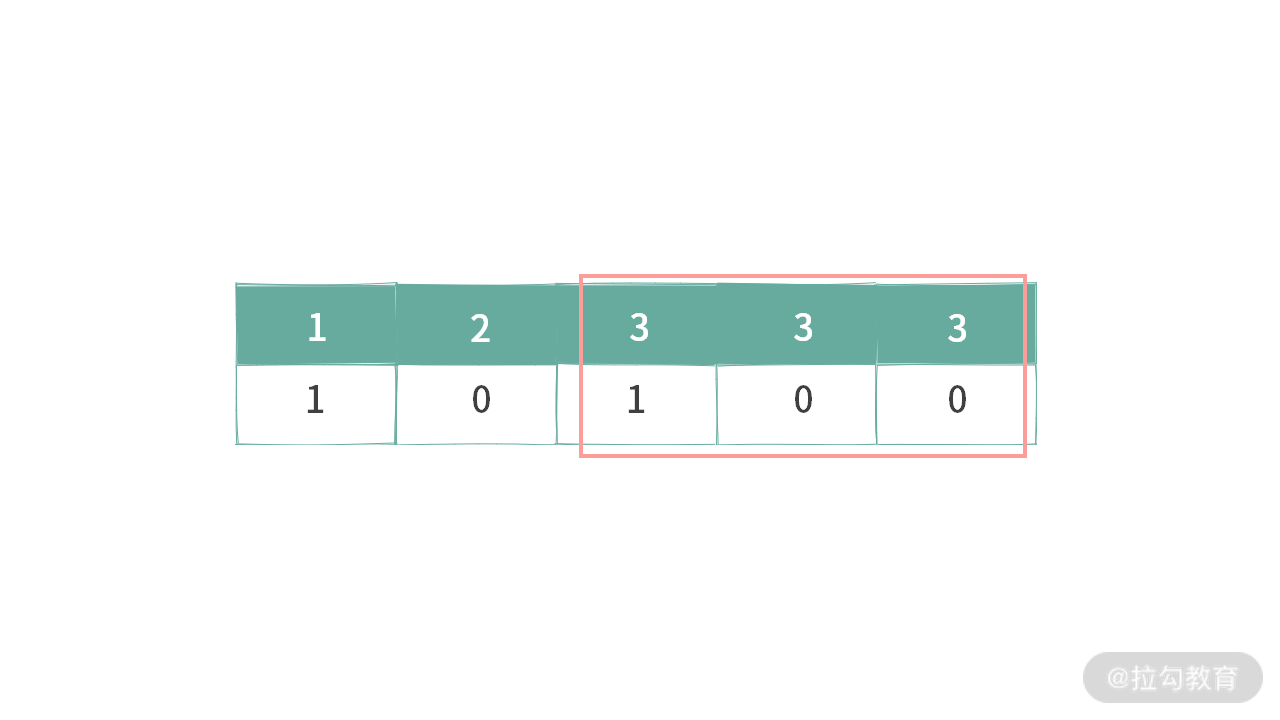
例 3,满足条件 1,也满足条件 2。针对相同元素 3 的 bit = 1 同时满足上面两个条件。
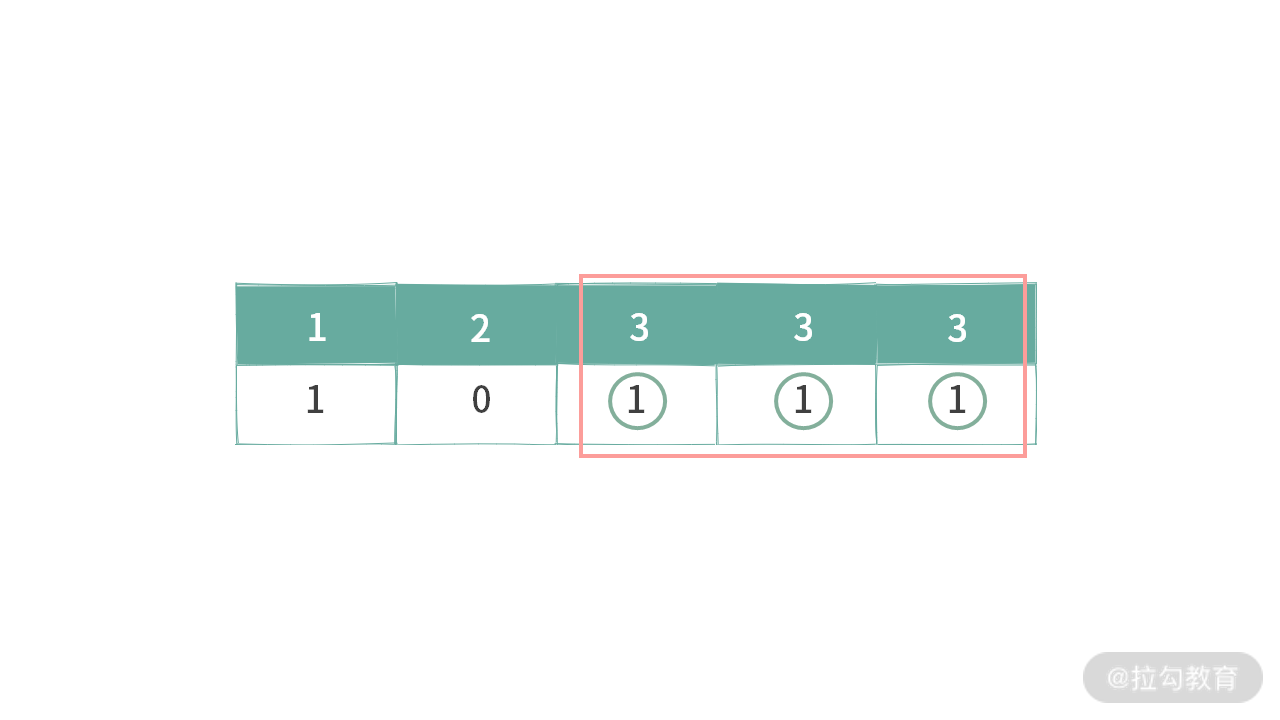
例 4,针对元素 3 的选择,同时满足两个条件。
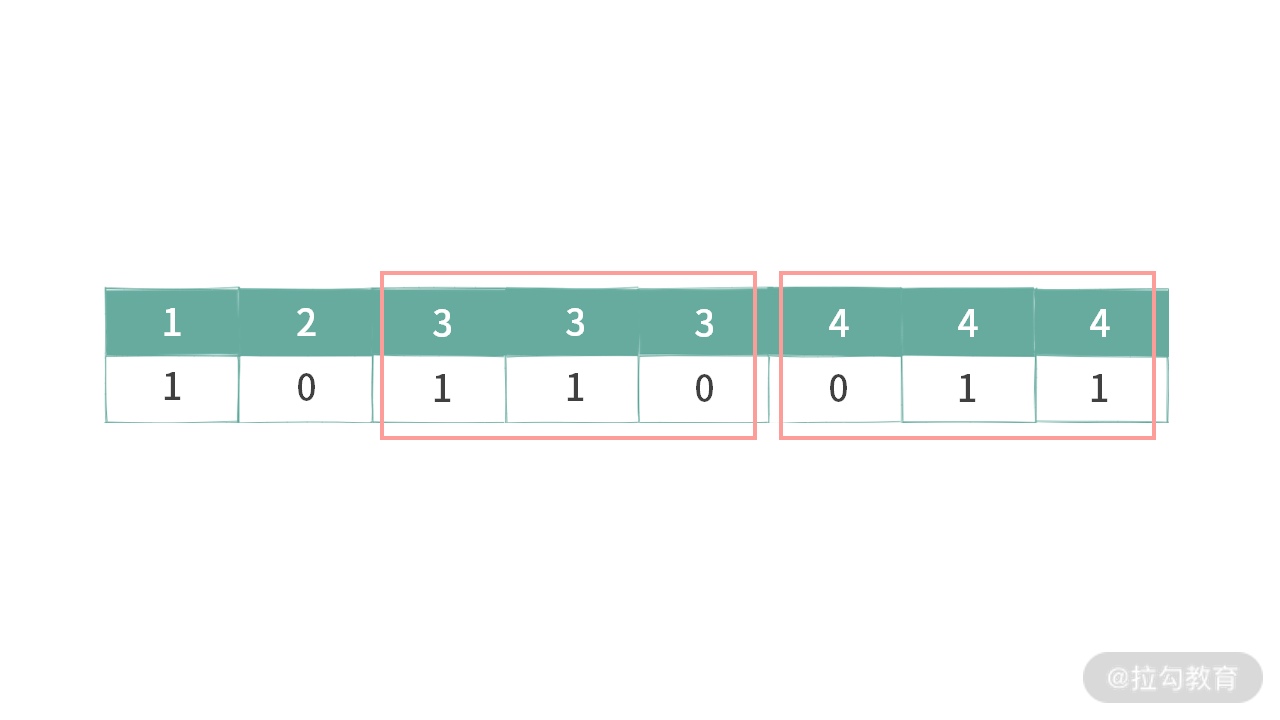
例 5,针对相同元素 3 和 4,其中元素 3 的 bit = 1 满足两个条件,但是元素 4 的 bit 位不满足条件 2。因此,这个二进制串也不满足两个条件。
那么按照这个规则,在生成子集的同时,我们还要检查一下二进制串是否满足条件 1 和条件 2。
注意:这里只是为了方便写代码,所以采用这个规则来挑选二进制串,挑选二进制串的方法并不是唯一的,你也可以选择其他简便的方法。
经过前面的分析,我们可以写出代码如下(解析在注释里):
class Solution {public List<List<Integer>> subsetsWithDup(int[] nums) {final int N = nums == null ? 0 : nums.length;Arrays.sort(nums);List<List<Integer>> ans = new ArrayList<>();for (int i = 0; i < (1<<N); i++) {List<Integer> subset = new ArrayList<>();boolean validSubset = true;for (int j = 0; j < N; j++) {if (j > 0 && nums[j] == nums[j-1]) {final int curBit = i & (1<<j);final int preBit = i & (1<<(j-1));if (curBit != 0 && preBit == 0) {validSubset = false;break;}}if ((i & (1<<j)) != 0) {subset.add(nums[j]);}}if (validSubset) {ans.add(subset);}}return ans;}}
通用方法 4:以退为进
接下来,我们重点讨论一下题目 2。在题目 2 去重的时候。如果我们再深入思考一下挑选二进制串的本质。不难发现,当数组为 A[] = {1, 2, 2, 2, 2} 时,我们只是想往子集中加入 2 的时候,分别往子集中添加:
那么,我们有没有可能采用下面这种思路?
首先记录数组中每个数出现的次数 hash[number] = count;接着,将数组中的元素去重。最后,当我们需要往子集中加入某个数的时候,只需要在题目 1 的基础上做一点变动:
选中某个数的时候,需要加入 1 个, 2 个, …, hash[number] 个这样的数。
处理题目 2 的过程,实际上是先退回了题目 1(这里我们选中了 BFS 算法),然后再在加入元素的次数上做了调整。
通过这种思路,就可以写出题目 2 代码如下(解析在注释里):
class Counter extends HashMap<Integer, Integer> {public int get(Integer k) {return containsKey(k) ? super.get(k) : 0;}public void add(int k, int v) {put(k, get(k) + v);if (get(k) <= 0) {remove(k);}}}class Solution {public List<List<Integer>> subsetsWithDup(int[] nums) {Counter cnt = new Counter();for (int x: nums) {cnt.add(x, 1);}List<List<Integer>> cur = new ArrayList<>();cur.add(new ArrayList<>());for (Map.Entry<Integer,Integer> en: cnt.entrySet()) {List<List<Integer>> next = new ArrayList<>();for (int addTimes = 1;addTimes <= en.getValue(); addTimes++) {for (List<Integer> subset: cur) {List<Integer> newSubset = new ArrayList<>(subset);for (int j = 0; j < addTimes; j++) {newSubset.add(en.getKey());}next.add(newSubset);}}for (List<Integer> subset: next) {cur.add(subset);}}return cur;}}
通用方法 5:分治
首先我们看一下题目 1,如果给定的数组 A[] = {1, 2}。实际上我们同然可以这样操作,得到所有的子集。
分治算法总是可以画成二叉树的样子,所以这里我们借助二叉树来展示分治的过程。
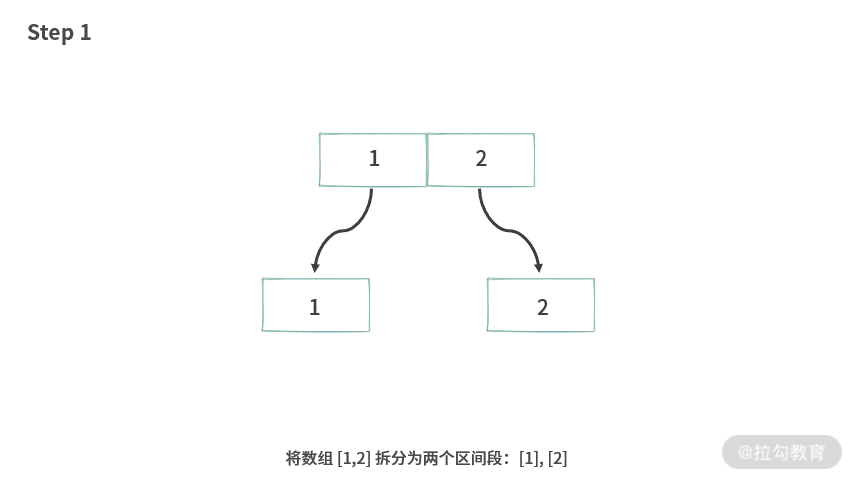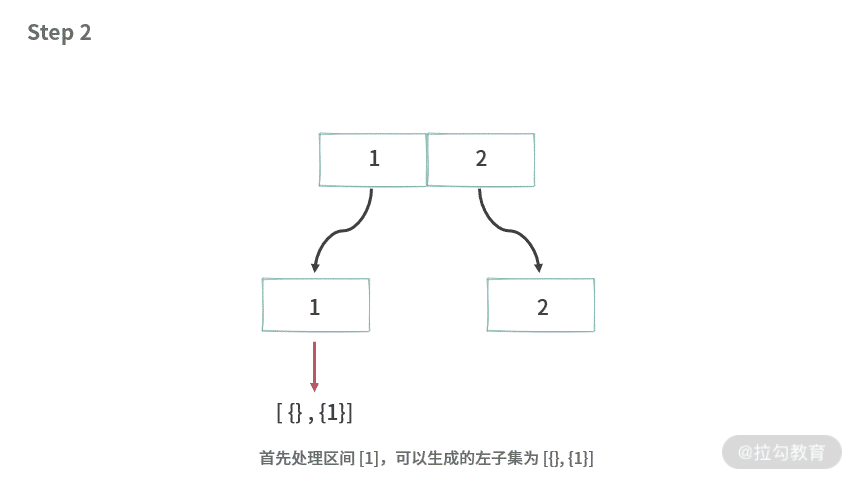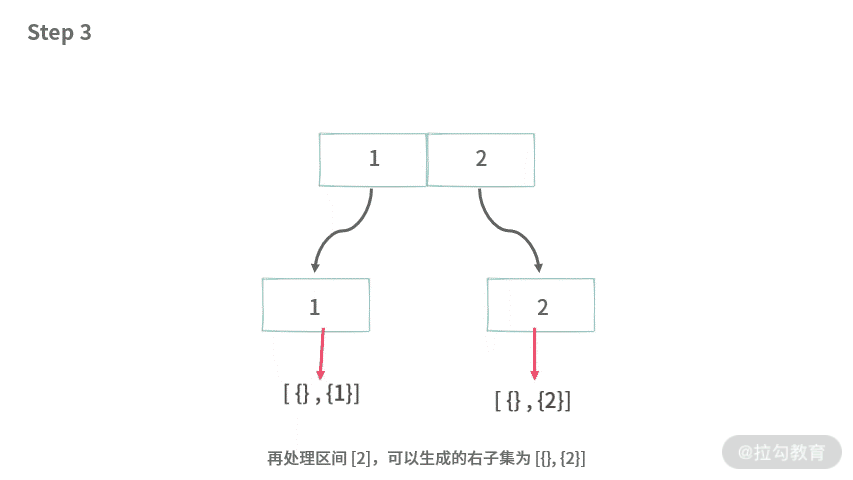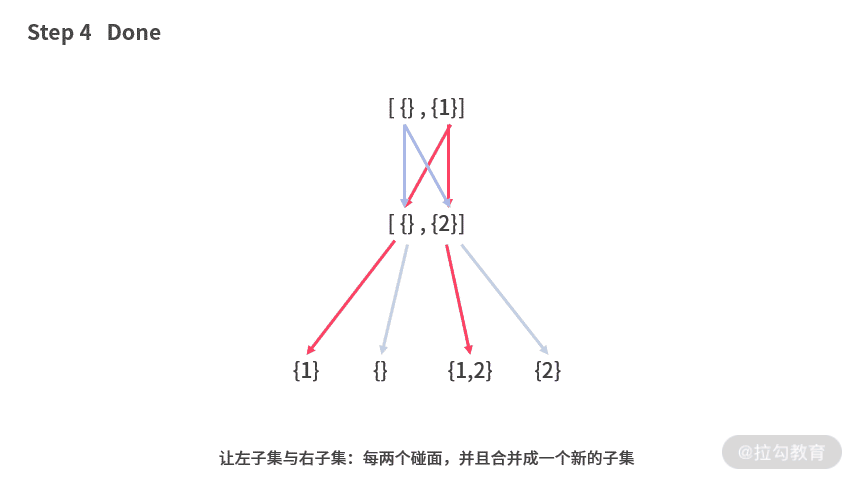
基于这种思想,可以得到题目 1分治的解法,代码如下:
class Solution {private List<Integer> merge(List<Integer> a, List<Integer> b) {List<Integer> tmp = new ArrayList<>(a);for (Integer x: b) {tmp.add(x);}return tmp;}private List<List<Integer>> dq(int[] nums, int b, int e) {List<List<Integer>> ans = new ArrayList<>();ans.add(new ArrayList<>());if (b >= e) {return ans;}List<Integer> tmp = new ArrayList<>();if (b + 1 == e) {tmp.add(nums[b]);ans.add(tmp);return ans;}final int mid = b + ((e-b)>>1);List<List<Integer>> l = dq(nums, b, mid);List<List<Integer>> r = dq(nums, mid, e);for (List<Integer> x: l) {for (List<Integer> y: r) {if (x.isEmpty() && y.isEmpty()) {continue;}ans.add(merge(x, y));}}return ans;}public List<List<Integer>> subsets(int[] nums) {final int N = nums == null ? 0 : nums.length;return dq(nums, 0, N);}}
代码:Java/C++/Python
我们需要格外注意空集的处理,合并的时候,如果两个集合都是空集,就不要再加入返回值了。因为它们之前已经加入空集(代码 13 行)了,重复加入会导致返回值中存在很多空集。
那么,我们应该如何处理题目 2 呢?如果仍然延续上述处理思路,在处理 A[] = {1, 2, 2, 2} 的时候,就会遇到问题。
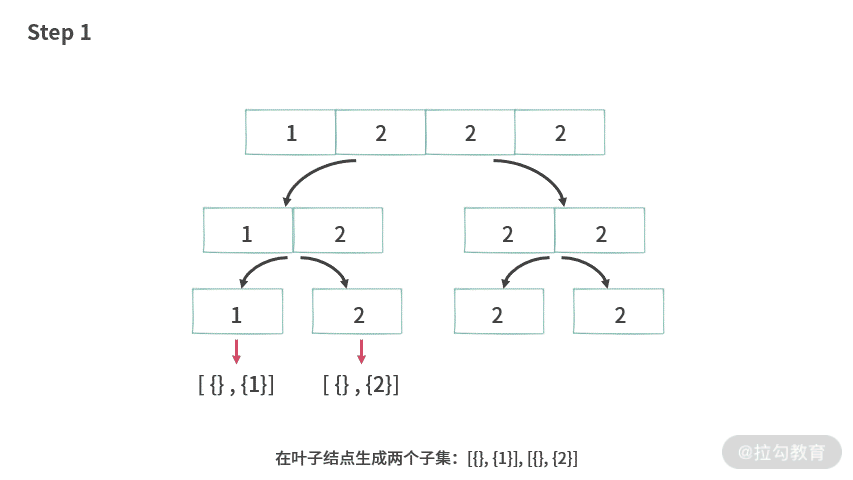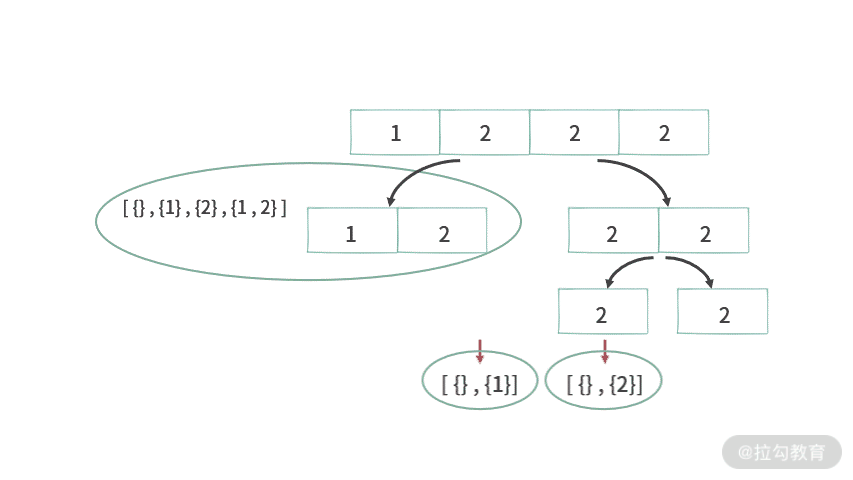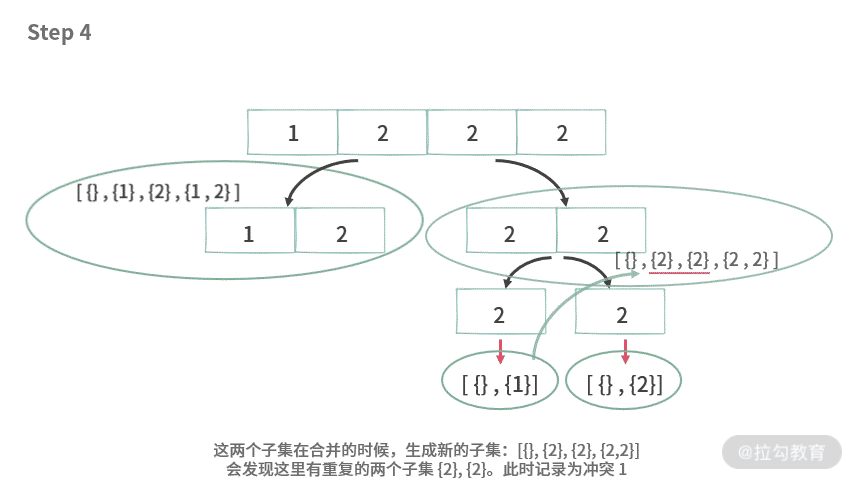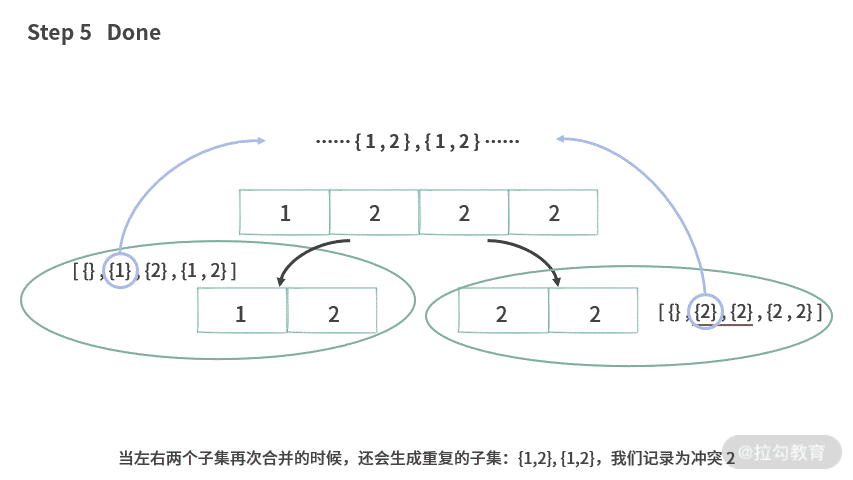
那么,有没有办法解决冲突 1 和冲突 2 呢?
首先来看冲突 1,产生冲突 1 的本质是因为,当数组已经被切分成 [2, 2] 的时候,实际上可以直接通过计算 2 的个数来生成子集。这里有 2 个 2,所以可以直接生成如下子集:
{}, 0个2{2}, 1个2{2,2} 2个2
也就是说,当数组里面的元素都是一样的时候,我们不能再进行切分。
那么再查看冲突 2。产生冲突 2 的根本原因在于:元素 2 分散在很多地方,每次合并的时候,都有可能生成重复的子集。在切分的时候,我们应该采用如下图所示的方法进行切分:
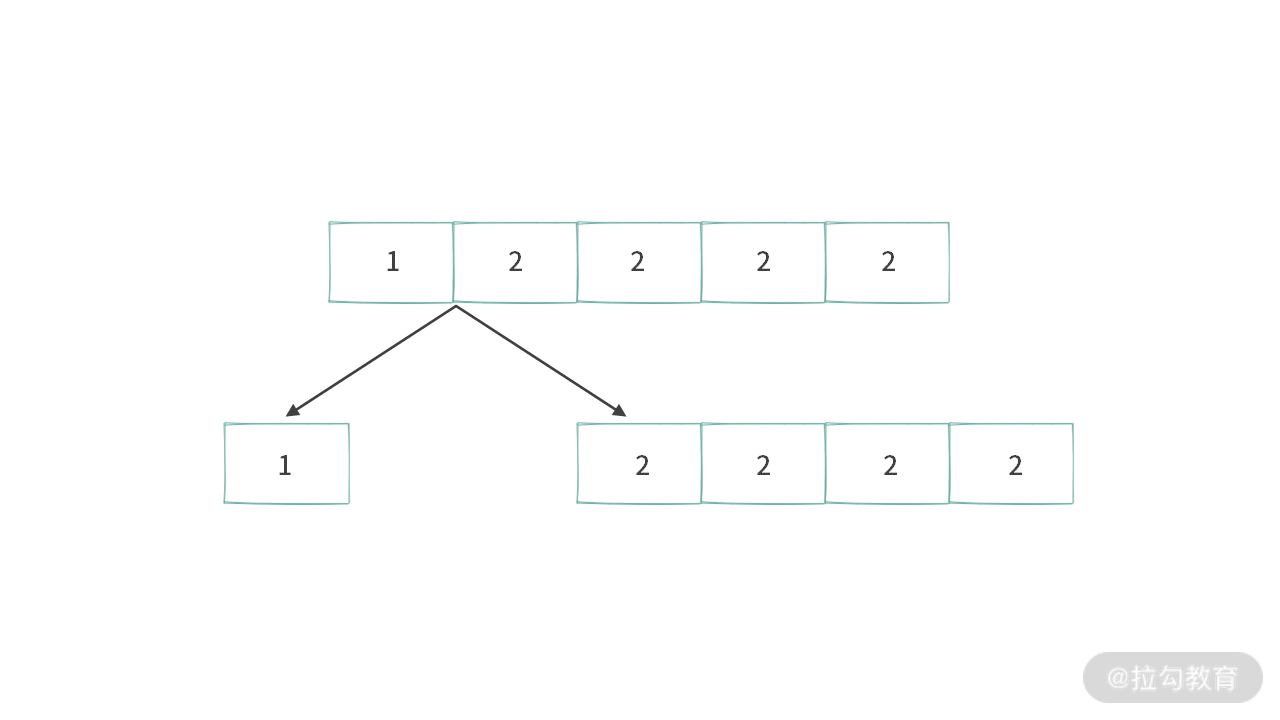
那么,这里可以总结为两个原则。
- 原则 1:当范围里面的数都是一样的时候,不能切分,而是采用计数的原则来生成子集。
- 原则 2:相同的数,不能被切分开,而是要当成一个整体。
基于这两个原则,我们就可以写出题目 2 的分治的代码了,如下所示(解析在注释里):
class Solution {private List<Integer> merge(List<Integer> a, List<Integer> b) {List<Integer> tmp = new ArrayList<>(a);for (Integer x: b) {tmp.add(x);}return tmp;}private boolean isSame(int[] nums, int b, int e) {boolean same = true;for (int i = b; i < e; i++) {if (nums[i] != nums[b]) {return false;}}return true;}private List<List<Integer>> dq(int[] nums, int b, int e) {List<List<Integer>> ans = new ArrayList<>();ans.add(new ArrayList<>());if (b >= e) {return ans;}boolean same =isSame(nums, b, e);if (same) {List<Integer> tmp = new ArrayList<>();for (int i = b; i < e; i++) {tmp.add(nums[i]);ans.add(new ArrayList<>(tmp));}return ans;}int mid = b + ((e-b)>>1);int l = mid - 1;while (l >= b && nums[l] == nums[mid]) {l--;}int r = mid;while (r < e && nums[r] == nums[mid]) {r++;}int cutPos = r;if (r >= e) {cutPos = l + 1;}List<List<Integer>> lans = dq(nums, b, cutPos);List<List<Integer>> rans = dq(nums, cutPos, e);for (List<Integer> x: lans) {for (List<Integer> y: rans) {if (x.isEmpty() && y.isEmpty()) {continue;}ans.add(merge(x, y));}}return ans;}public List<List<Integer>> subsetsWithDup(int[] nums) {if (nums == null || nums.length == 0) {return new ArrayList<>();}Arrays.sort(nums);return dq(nums, 0, nums.length);}}
总结
在本讲,我们通过分析题目的不同特点,展开了不同的解题思路,构造出了 5 种不同的解法。这里,我将 5 种解法进行了一个总结,如下图所示:
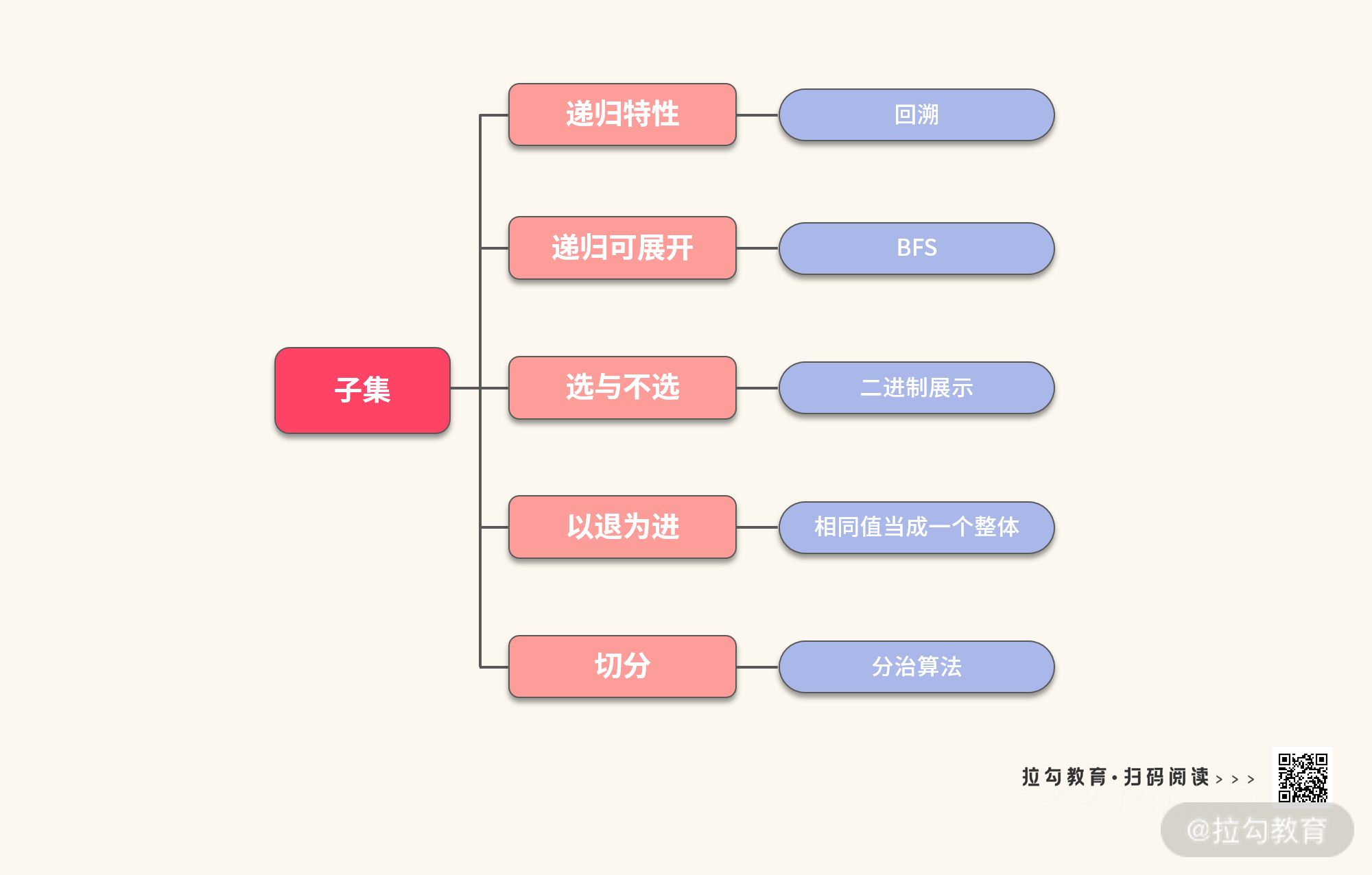
题目是做不完的,但是我们可以通过分析每一个题目来锻炼挖掘题目信息的能力,以及匹配到我们大脑中已经存储的数据结构与算法的能力。同时,也可以通过这种方式,将学会的知识变成我们解决问题的能力,只有这样 “学习” 才能变成“学会”。
思考题
最后,我再给你留一个思考题:在求解题目 2 的每一种方法中,我们都提前对数组进行了排序的处理,每次排序的原因和目的分别是什么?
可以把你的分析写在留言区,我们一起讨论。如果你觉得今天的内容对你有所启发,欢迎分享给身边的朋友。
好了,子集问题我们就学习到这里,希望你还能找出更多有趣的解法。接下来让我们前进到 18 | 单词接龙:如何巧用深搜与广搜的变形?记得按时来探险。

