数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
回溯算法本质上是一种 DFS 算法,在一些小的数据集上能够找到最优解。因此,遇到穷举所有路径的问题时,就需要用到回溯。比如,在一些外卖派单系统中,大数据系统给骑手派单,在某个单位时间内累积的订单总是有限的,此时就可以利用回溯算法求解最优派送时间。
在互联网公司的面试中,面试官也会经常考察应聘者对小范围数据找最优解的能力。此时,回溯就是一个非常适合的考点。
在本讲中,首先我们会讲清楚回溯的由来,以及回溯算法的 1 个核心和 3 个条件。然后,介绍回溯算法的应用:
- 排列 / 组合问题
- 去重排列 / 组合问题
学完本讲,你将收获 “一招鲜” 的回溯模板。
在开始学习之前,我给你提 2 个醒儿:
- 我会从简单的问题开始讲解,哪怕你已经知道很多例题的标准答案,也不妨再跟着我学习一遍,也许会有不一样的感悟。
- 本讲会采用链式推导的方式进行讲解,虽然从一个简单的知识点开始讲述,但请你尽量不要跳着读,这样理解起来会更顺滑。
从一次面试开始
在拿出模板之前,我们先进行一场模拟面试。很多面试官喜欢从一个非常简单又细小的问题开始层层推进,逐步加深问题的难度,因此本讲我们也采用这种思路进行讲解。
注:在面试时,回答简单的问题要非常小心,避免犯错,这样面试官才愿意继续和你深入探讨,后面肯定有条 “大鱼” 等着你去抓。
从循环到递归
假设这个简单的问题为:需要打印一个数组。比如给定的数组 A[] = {1,2,3},那么我们需要打印为:
{}{1,}{1, 2}{1, 2, 3,}
此外,面试官还给你提供了一个打印函数,你的实现需要用到它:
void print(int[] A, int i) {System.out.print("{");for (int j = 0; j < i; j++) {System.out.print(A[j] + ", ");}System.out.println("}");}
老司机的故事:如果面试官说,你需要使用某个函数,其意就是告诉你必须要用它!曾经我有一位朋友在面试中挂掉了,原因就是:面试官指定使用 nextRandomInteger() 函数,他却用了 Math.rand() 库函数,导致最后没能通过面试,所以你一定要吸取经验。
利用给定的 print() 函数,根据题目要求:你应该可以写出如下代码:
static void solve(int[] A) {final int N = A == null ? 0 : A.length;for (int i = 0; i <= N; i++) {print(A, i);}}
当面试官看了你的代码,觉得没有问题之后,又将题目进行了升级。面试官让你将这个代码转换为递归的方式。对于这种一维的递归,想必你也能很快拿下吧。
void solve2(int[] A, int i) {final int N = A == null ? 0 : A.length;if (i > N) {return;}print(0, i);solve2(A, i + 1);}
经过前面一小轮的交流,相信你已经明白面试官的考点就是:
- 循环边界
- 指定函数的使用
- 递归
难度升级 1
面试官一看这些问题都没能难住你,并且还有很多时间,接下来:
- 希望你在递归的基础上改进代码
- 需要使用一个数据结构 Box 来完成打印操作
这个 Box 数据结构有 push、pop、print 三个函数,定义如下:
class Box {private List<Integer> l = new ArrayList<>();public void push(int x) { l.add(x); }public void pop() { l.remove(l.size() - 1); }public void print() {System.out.print("{");for (Integer x : l) {System.out.print(x + ", ");}System.out.println("}");}}
老司机的提醒:既然面试官提到了 “需要使用”,那就是要求你必须使用。于是你经过一番琢磨写出如下代码:
void solve3(int[] A, int i, Box s) {final int N = A == null ? 0 : A.length;s.print();if (i >= N) {return;}s.push(A[i]);solve3(A, i + 1, s);}
面试官点了点头,正当你在想为什么没有用到 pop() 函数时,面试官就再次将难度进行升级了。
难度升级 2
面试官会问:如果要用 pop() 函数,应该放在什么地方呢?
老司机的提醒:在这种需求多变的面试场景里,你一定要紧跟面试官的思路。此时耐心非常重要。毕竟,工作上的需求就是灵活又多变的。
在面试官的连环追问下,你可能需要想一段时间,代码就会变成这样:
void solve4(int[] A, int i, Box s) {final int N = A == null ? 0 : A.length;s.print();if (i >= N) {return;}s.push(A[i]);solve4(A, i + 1, s);s.pop();}
如果你觉得 s.pop() 突然让代码变得很难理解了,不要着急,接下来我会用一种更容易理解的方式给你讲解。
我们来玩一种借箱子的游戏。每个玩游戏的人,从左到右排成一排,需要遵守以下规则:
- 每个人刚借到箱子的时候,公布箱子的状态(不公布的话,万一别人耍赖说里面有一个亿,到时候咱们可还不起);
- 把自己选的 “宝石” 放到箱子中(我们暂且假设第 i 个人,只能选 A[i] 号宝石);
- 把箱子借给右边的人;
- 为了避免弄丢东西,每个人都必须遵守规则:归还的箱子要与借出时一模一样,所以归还箱子的时候,需要把箱子里面的属于自己的东西拿出来。
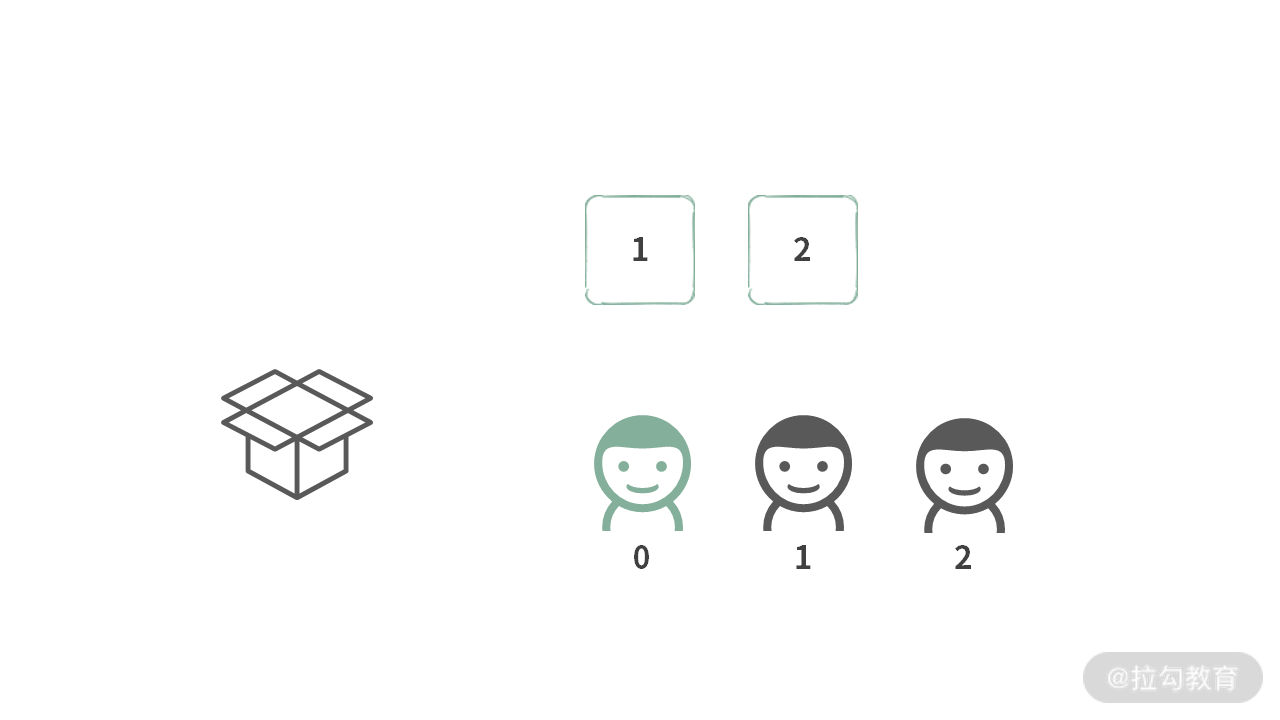
我们先看一下数组中有两个元素的时候应该如何处理。
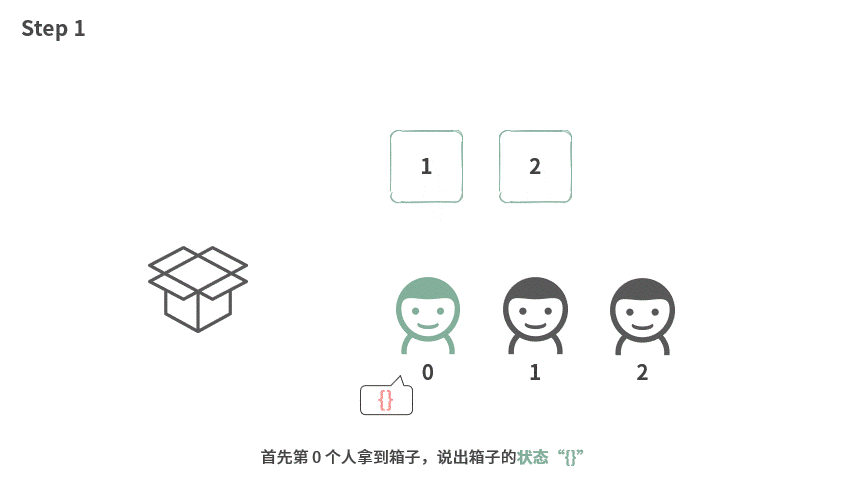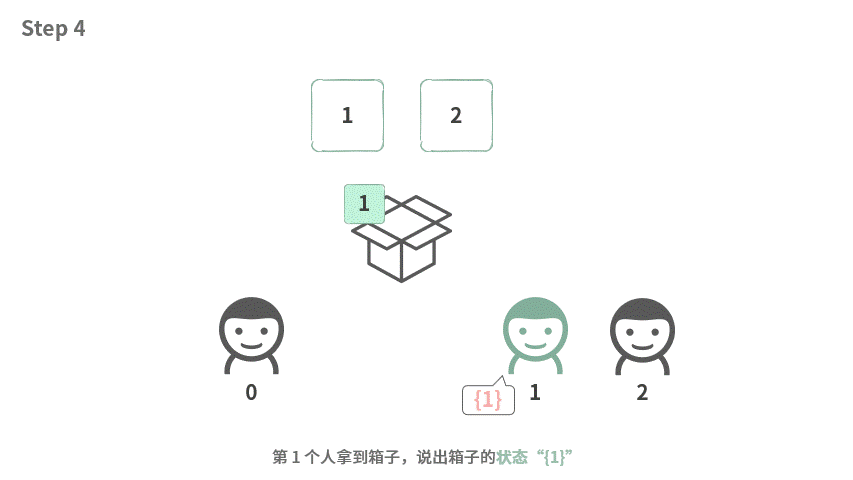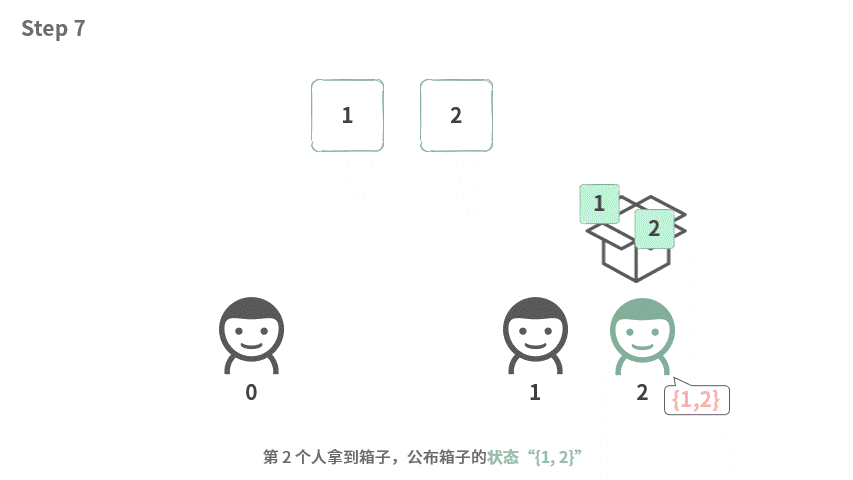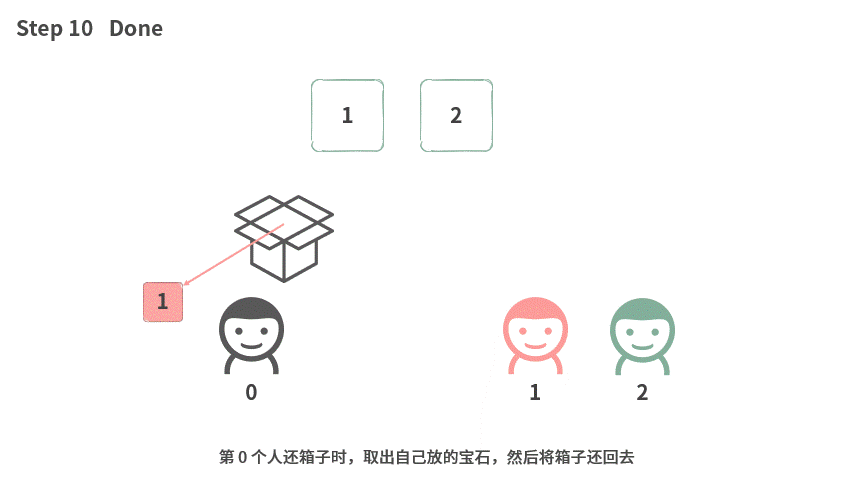
这个时候,输出的结果刚好如下:
如果我们把视角固定在某个人身上,他要做的事情就是:
- 说出拿到箱子的状态
- 把自己的东西放进去
- 借出箱子
- 把自己的东西拿出来,把箱子还回去。
这样,我们也同样完成了所有状态的输出。下面将 solve4() 函数加点 “玩游戏” 的注释。
void solve4(int[] A, int i, Box s) {final int N = A == null ? 0 : A.length;s.print();if (i >= N) {return;}s.push(A[i]);solve4(A, i + 1, s);s.pop();}
现在我们应该已经明白 s.pop() 的含义了。
注意:图中数组长度为 2,里面一共有第 0、第 1、第 2 个人。当 if (i >= N)的时候,也就是第 2 个人实际上不可以选择 A[2]。因为这里包含 3 个含义:
- 如果访问 A[2] 就会导致访问数组越界
- 第 2 个人不能选择任何宝石。也就是没有任何选项
- 更进一步,第 3、第 4、第 5 个人肯定也是没有任何选择的,所以后面需要直接返回。
所以 if (i >= N)表示的本质是:[N, .., inf) 后面所有的人都不会有任何选项了!所以直接返回即可!
因此,你平时读算法时,如果觉得一段代码非常难懂,除了要一步一步去调试,你还需要为这段代码找一个有趣的场景。
现在的情况是,每个人都只能有一个宝石,那么如果每个人都有两个宝石,代码就可以进化成这样(解析在注释里):
void solve5(int[] A, int i, Box s) {final int N = A == null ? 0 : A.length;s.print();if (i >= N) {return;}s.push(第i个人的宝石1);solve5(A, i + 1, s);s.pop();s.push(第i个人的宝石2);solve5(A, i + 1, s);s.pop();}
但是代码这么写,显得很啰唆。那有没有什么更好的办法呢?
模板
前面我们在玩 “借箱子” 游戏的时候,直接输出了所有的 “箱子” 的状态。但是有时候,并不是所有的状态都需要输出,你需要根据题目的条件决定哪些应该作为答案进行输出。因此,在 solve5() 函数的基础上,一个更具有普适性的回溯模板就准备好了(解析在注释里):
void backtrace(int[] A,int i,Box s,answer) {final int N = A == null ? 0 : A.length;if (状态满足要求) {answer.add(s);}if ([i, ...., 后面)的人都没有任何选项了) {return;}for 宝石 in {第i个人当前所有宝石选项} {s.push(宝石);backtrace(A, i + 1, s, answer);s.pop();}}
注意:一般来说,回溯的题目都出得比较 “赤裸裸”,基本上不需要经过分析匹配,可以直接套这个模板。
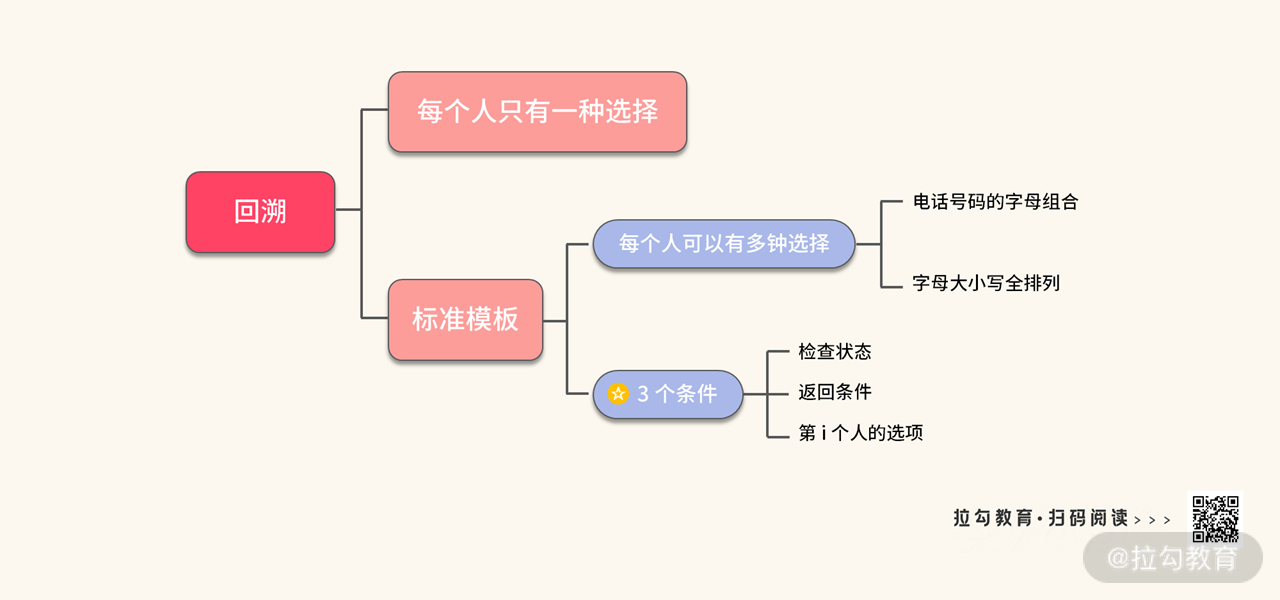
这里稍微总结一下我们得到回溯模板的推导过程:
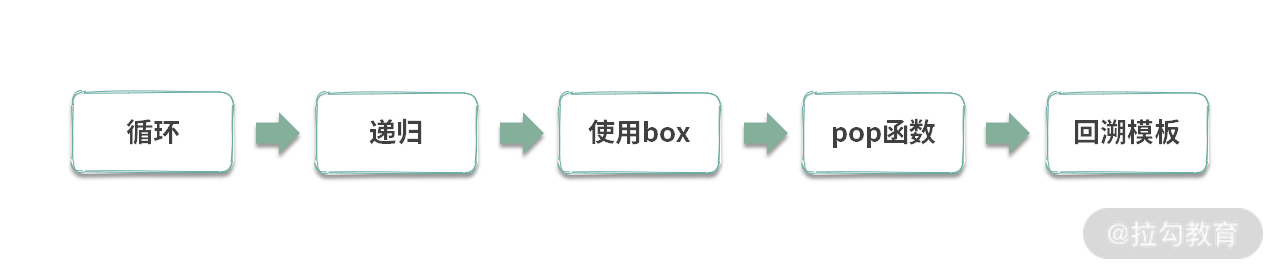
接下来我们看一下使用这个模板所需要:
- 1 个核心
- 3 个条件
1 个核心
理解回溯算法的核心,可以将思路的重点总结为:第 i 个人怎么选?
其他人的情况都被我们无视了。因为,如果从全局的角度去思考问题,你会发现递归来,递归去容易把人绕晕。反过来,如果你考虑清楚第 i 个人应该如何做选择,那么回溯算法就可以迎刃而解。
3 个条件
当我们解决一个核心的问题之后,接下来就要着手开始写代码的时候,需要解决 3 个条件:
- 什么样的状态是我们想要的?
- 后面的人还有选项吗?如果后面所有的人都没有选项,就需要返回了。
- 第 i 个人的宝石选项是什么样的?
排列组合问题
排列组合在面试中出现的概率极高。尤其是微软,头条等大厂特别喜欢出相关的题目。
排列组合题目,基本上都是使用回溯算法进行求解。熟练地使用回溯的模板,是击破这些大厂算法面试的必要条件。
接下来,我们将由浅入深地展开排列组合中的经典面试题。
例 1:电话号码的字母组合
【题目】给定一个手机拨号盘,不同的按键对应不同的字母。现在给定数字字符串的输入,你需要返回所有的小写字母的组合。(条件:输入的数字只会有 2~9)。

输入:A = “23”
输出:[“ad”,”ae”,”af”,”bd”,”be”,”bf”,”cd”,”ce”,”cf”]
解释:数字 2 可以选择字母 “abc”, 数字 3 可以选择 “def”。那么一共有 9 种组合。
【分析】看到 “所有” 二字,你应该立马想到使用回溯算法。前面我们提到。回溯算法需要 1 个核心和 3 个条件。
1. 1 个核心
回想一下之前的 “借箱子” 游戏,里面每个人都只可以有一种选择。
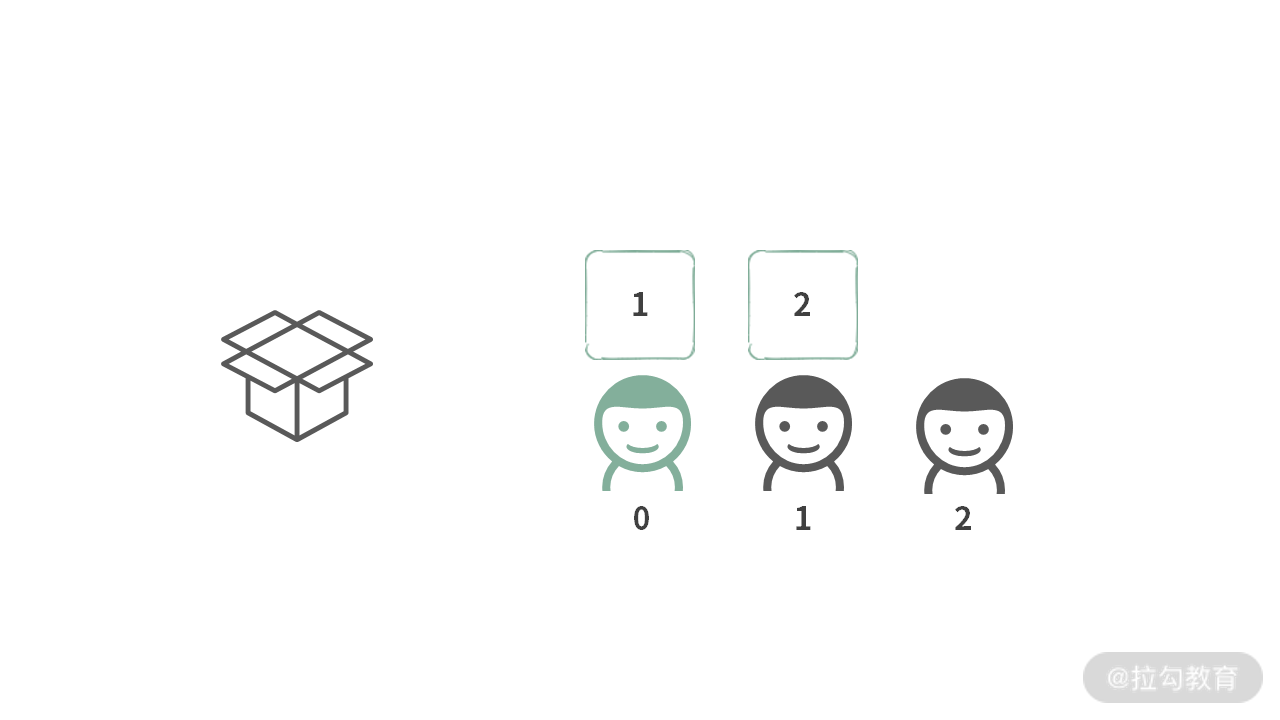
而现在,当题目改变,输入变成 “23” 之后,情形如下:
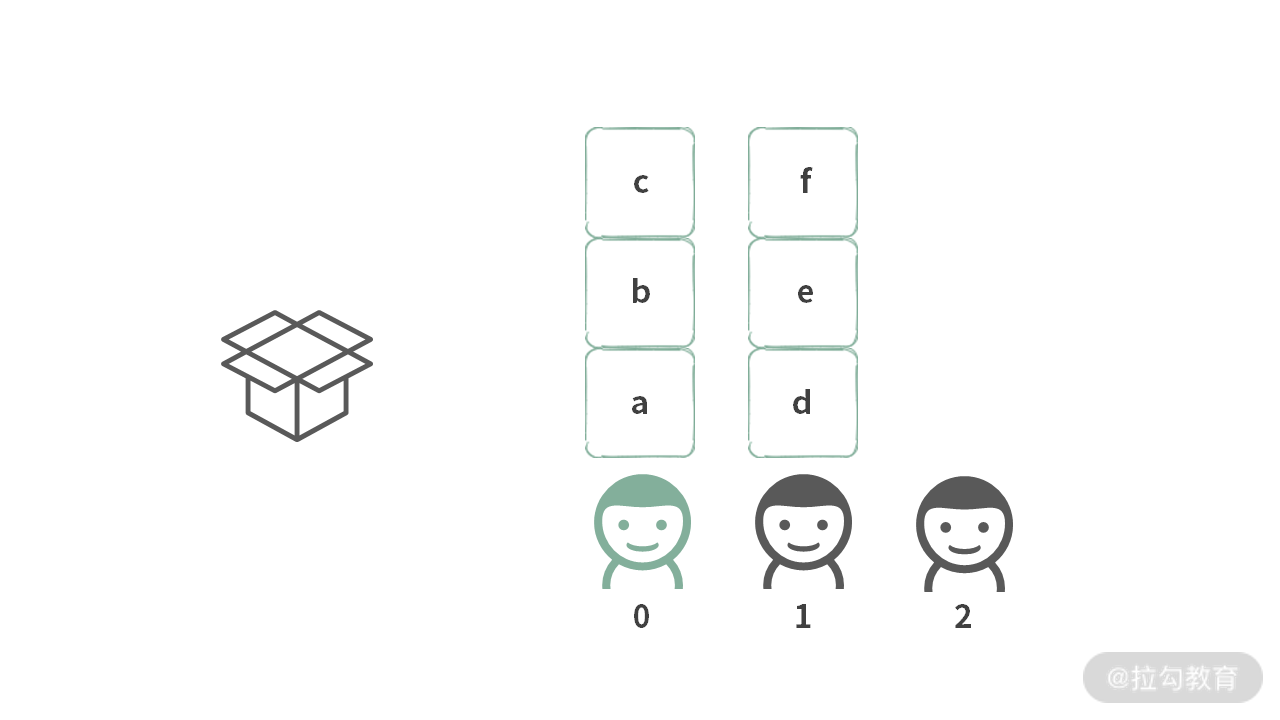
第 0 个人拿到的是数字 2,可以选择的 “宝石” 为{“a”, “b”, “c”},第 1 个人可以拿到的宝石为{“d”, “e”, “f”}。
因此,第 i 个人的选择是:
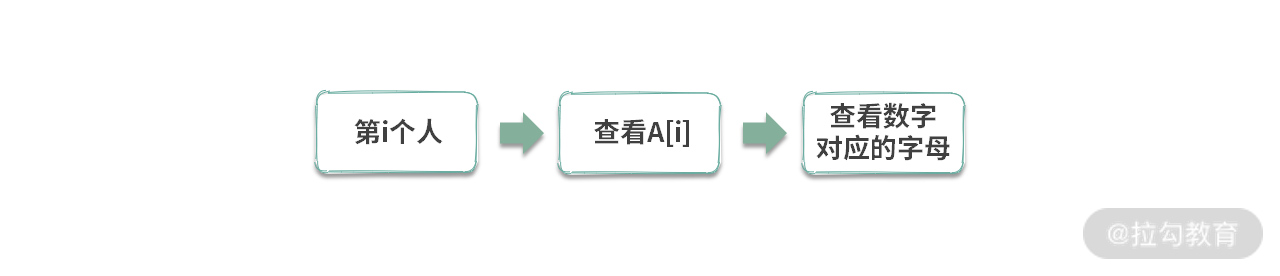
同时,这里我们可以发现,第 i 个人,与 A[i] 并不是强强绑定的。有时候只是借助 A[i] 完成映射。
2. 3 个条件
如果想要直接套用回溯模板,请你先回答一下回溯模板的三个问题。
1)什么样的 “箱子” 状态是我们想要的?
在这个题目中,由于要输出所有的数字的完整组合,那么只有 “箱子” 状态的长度等于输入字符串长度的时候,才是满足要求的。
2)什么时候返回?
输入字符串长度为 n,那么返回条件应该是 if (i>= n) 就需要返回。 因为从 i = n 个人,就不会有宝石选择了。
3)每个人的宝石选项如何处理?
正常情况下,第 i 个人的宝石就应该是 A[i],但是题目中已经指出,A[i] 对应的是一个数字,然后再通过数字得到相应的字母。比如 A[0] = ‘2’,那么第 0 个人通过字符 ‘2’ 就可以选择 {“a”, “b”, “c”} 三种宝石。
【代码】通过前面的分析,到这里,我们已经可以直接套用回溯模板写代码了(解析在注释里):
class Solution {final String[] ds = new String[] {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};void backtrace(String A, int i, StringBuffer box, List<String> ans) {final int N = A == null ? 0 : A.length();if (box.length() == N) {ans.add(box.toString());}if (i >= N) {return;}final int stoneIndex = (int) (A.charAt(i) - '0');for (int idx = 0; idx < ds[stoneIndex].length(); idx++) {Character stone = ds[stoneIndex].charAt(idx);box.append(stone);backtrace(A, i + 1, box, ans);box.deleteCharAt(box.length() - 1);}}public List<String> letterCombinations(String A) {if (A == null || A.length() == 0) {return new ArrayList<>();}StringBuffer box = new StringBuffer();List<String> ans = new ArrayList<>();backtrace(A, 0, box, ans);return ans;}}
复杂度分析:如果字符串总长为 L,字符串中有 a 个字符属于 {‘7’, ‘9’},都可以映射到 4 个字母。有 b 个字符属于 {‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘8’},都可以映射到 3 个字母上。那么复杂度为 O(4a x 3 b)。除去返回值占用的空间,那么只需要占用 O(L) 的空间。
【小结】相比而言,这道题对应的回溯模板还是比较 “赤裸裸”,直接套用模板就能解决。但是你要注意“回答” 模板的 3 个条件。我再给你留一道练习题,希望你不要偷懒,完成练习巩固这个知识点。
练习题 1: 给定只有数字和字母的字符串,其中字母可以改成大写和小写。请输出所有的改写可能。
输入:A = “a3”
输出:[“A3”, “a3”]
至此,我们已经从每个人只有一种选择,推导到每个人有多种选择。
例 2:子集
【题目】给定一个互不相同的数的数组,返回这个数组里面所有的可能的子集(包括空集)。要求里面的子集不能重复。比如 [[1,2], [2,1]] 不合要求。因为这两个集合是一样的。
输入:A = [1, 2, 3]
输出:[[],[1],[1,2],[1,2,3],[1,3],[2],[2,3],[3]]
解释:A = [1, 2,3] 集合的子集有 : 分别是 [[],[1],[1,2],[1,2,3],[1,3],[2],[2,3],[3]]。
【分析】当一看到子集,就应该想到回溯,接着联系到回溯的模板代码。现在,我们面临的问题是,如何决定每个人选择的宝石应该是什么?
1. 1 个核心
首先假设,每个人都可以选择所有的宝石。那么游戏就会形成如下:
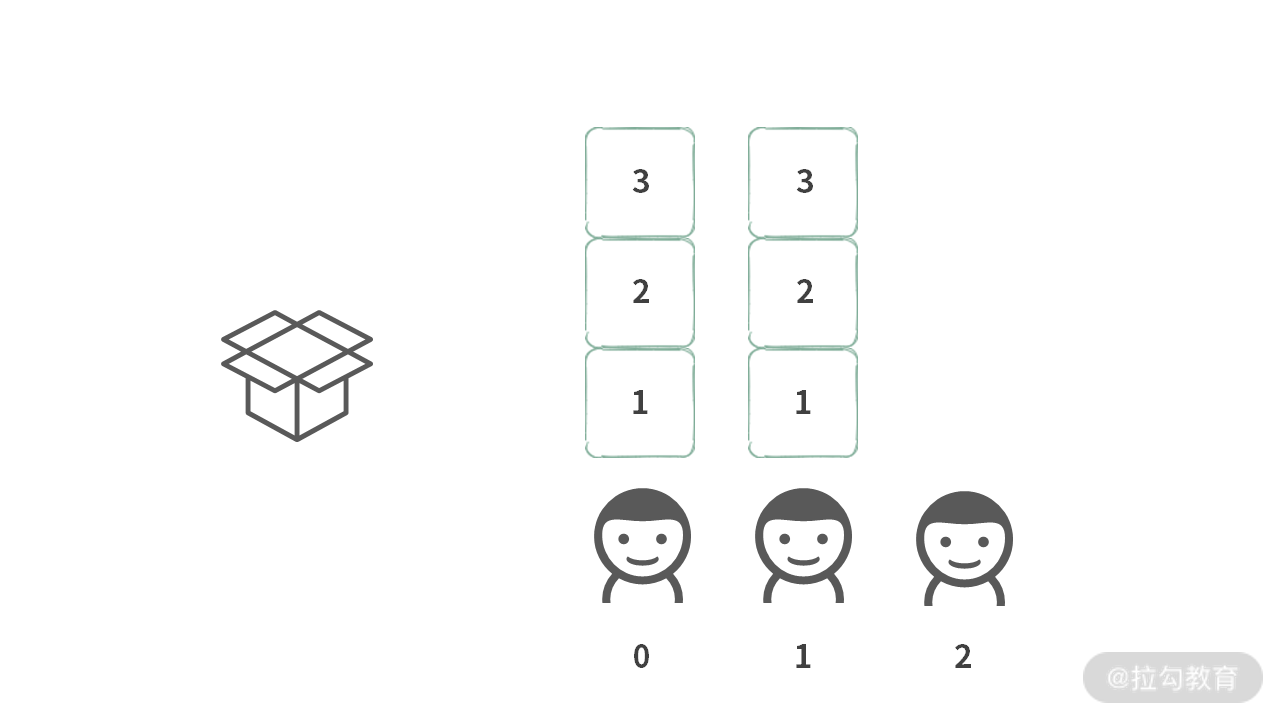
但是,如果第 0 个人选择 1 ,此时第 1 个人也选择 1,那么箱子里面会装上 “{1, 1}”。很明显这是不符合要求的,因为一个元素被用了两次,不符合子集的定义。
我们分情况整理如下:
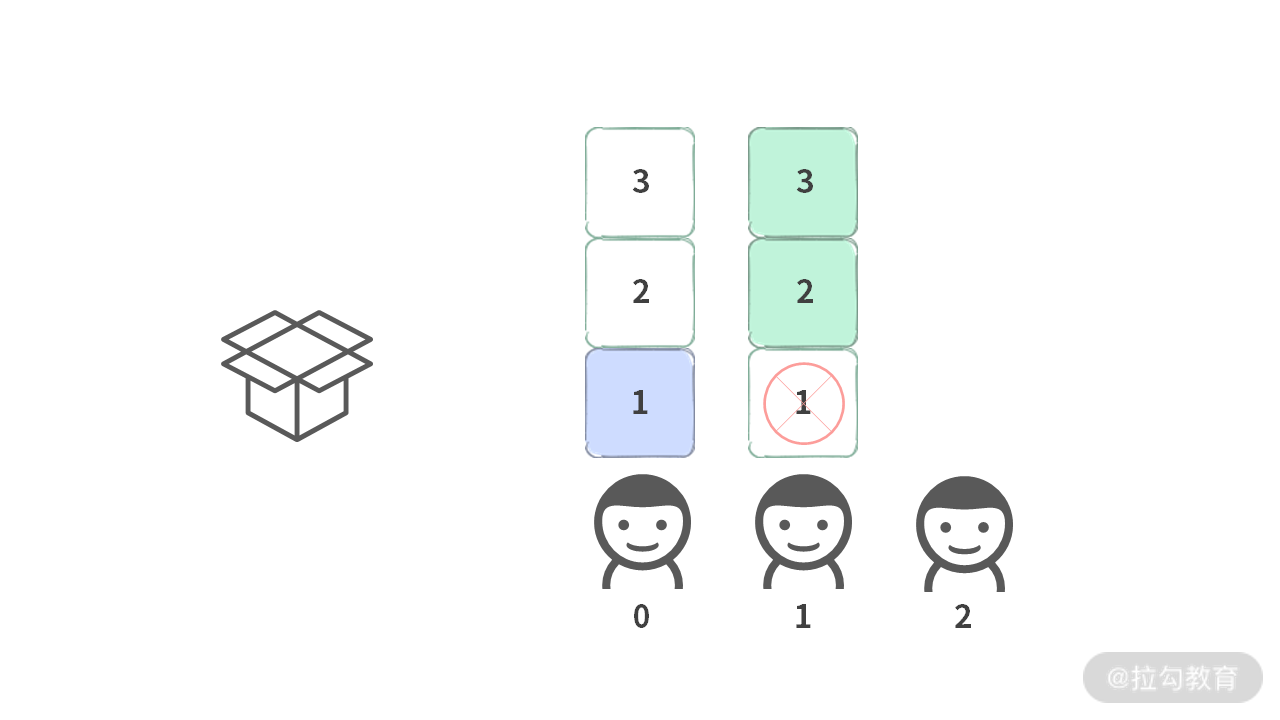
Case 1. 当第 0 个人选择 1 的时候,第 1 个人只能选择 {2, 3}, {1, 2}, {1, 3}。
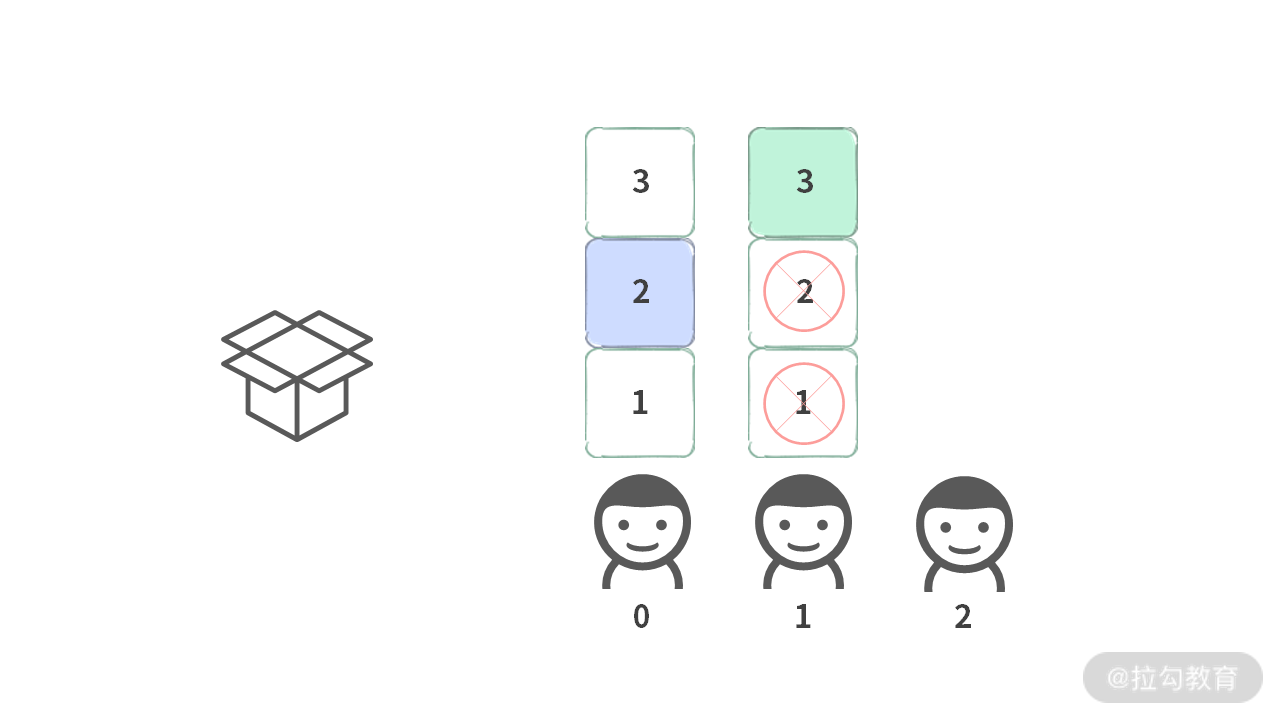
Case 2. 当第 0 个人选择 2 的时候,第 1 个人只能选择 {3}。注意,此时不能再去选择 1,否则会形成 {2, 1},而这种情况是在前面的选择中出现过的。
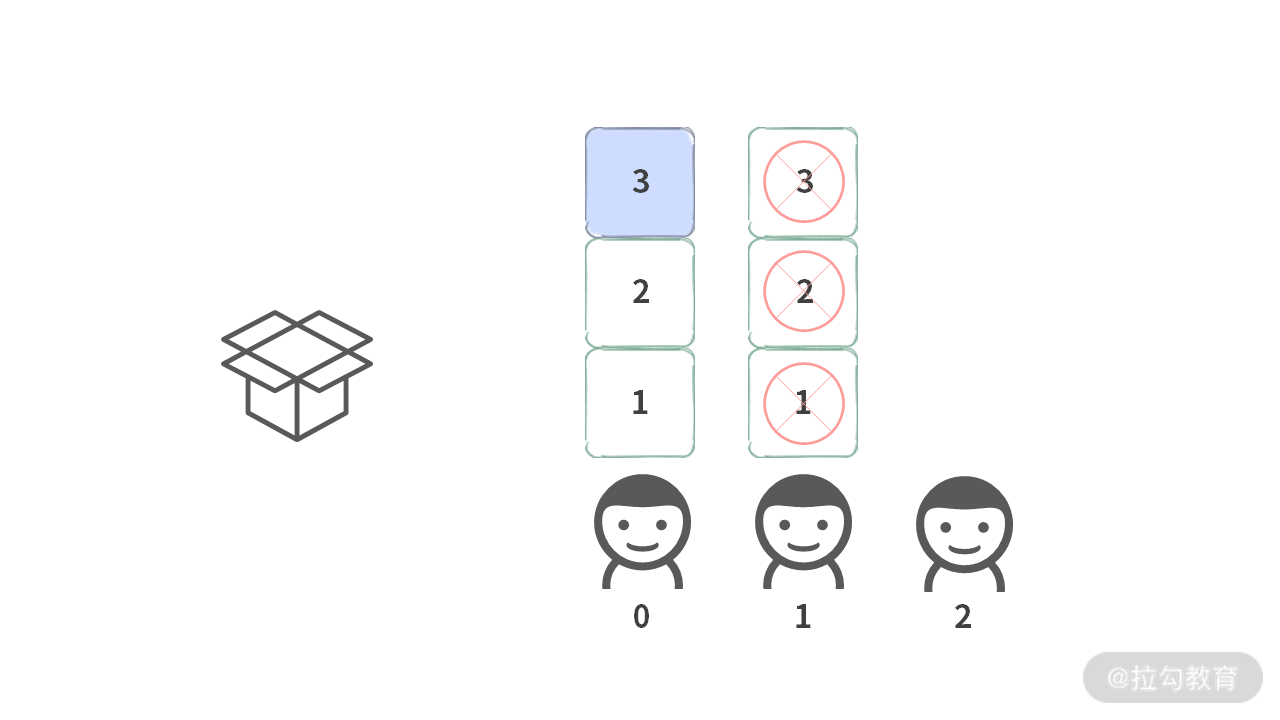
Case 3. 当第 0 个人选择 3 的时候,第 1 个人所有的数都不能选。因为一选就会和 Case 1,、Case 2 重复。
通过上述分析,我们发现,第 1 个人的选择范围是和第 0 个人的选择有关系的。如果第 0 个人选择了下标 A[j],那么第 1 个人就只能选择数组 A[] 中第 [j + 1, …, N) 范围里面的 “宝石”。
可以总结成结论 1:
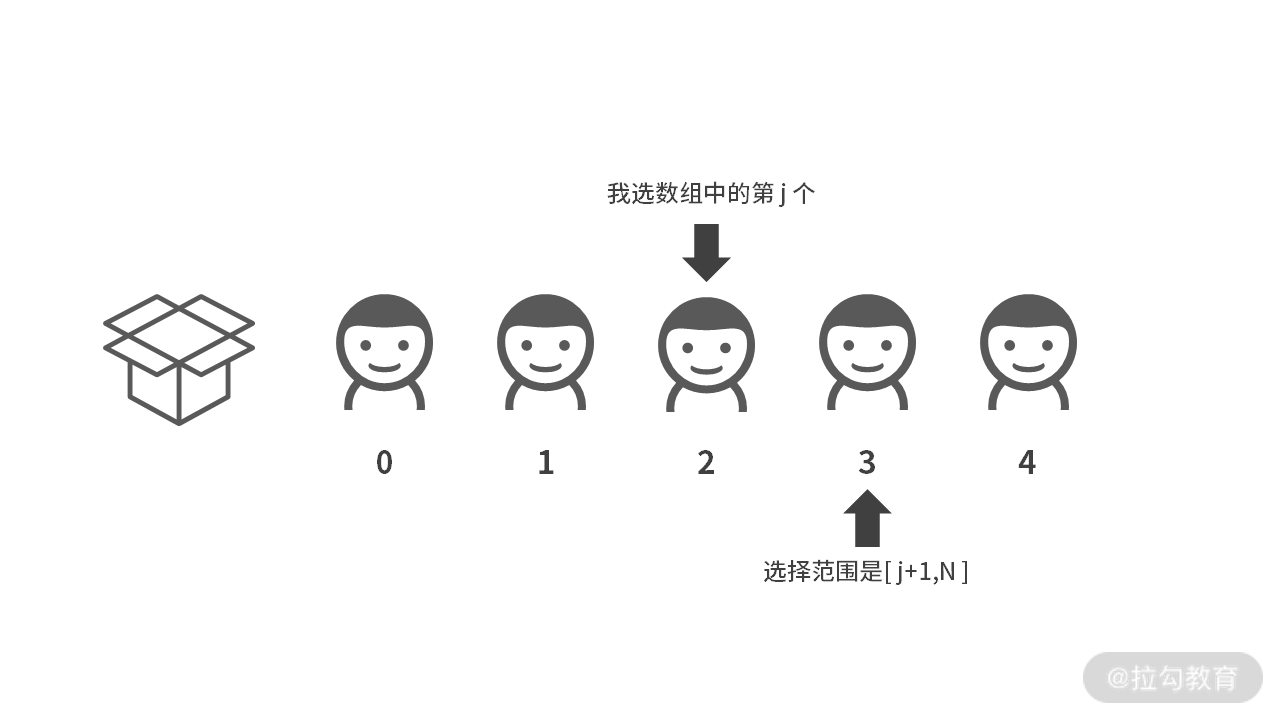
如果第 i 个人选择 A[j],那么第 i+1 个人的选择范围就是 A[j + 1, N)
2. 3 个条件
在写代码之前,我们再回答一下回溯代码的 3 个条件。
1)什么样的 “箱子” 状态是我们想要的?
这时是要所有的子集,所以我们只需要把所有的 box 状态放到 ans 中。
2)什么时候返回?
输入字符串长度为 n,那么当 if (i>= n) 就需要返回。 因为从 i = n 个人,就不会有宝石选择了。
3)每个的宝石选项如何处理?
当第 i 个人选择了 A[j],那么第 i + 1 个人就只能选择 [j + 1, N)。
那么我们可以写出代码如下(解析在注释里):
void append(List<Integer> box, List<List<Integer>> answer) {answer.add(new ArrayList<>());for (Integer x: box) {answer.get(answer.size()-1).add(x);}}void backTrace(int[] A,int i,int begin,int end,List<Integer> box,List<List<Integer>> answer) {final int N = A == null ? 0 : A.length;append(box, answer);if (i >= N || begin >= end) {return;}for (int j = begin; j < end; j++) {box.add(A[j]);backTrace(A, i + 1, j + 1, end, box, answer);box.remove(box.size()-1);}}
这里我们根据模板写出了代码,仔细观察可以发现,有以下 2 个地方可以优化:
- i 变量其实没有什么用,仅在传参数的时候传了 i + 1 递归下去;
- end 变量其实就是 N,没有必要写在参数里面。
【代码】经过一轮优化后的代码如下(解析在注释里):
void append(List<Integer> box, List<List<Integer>> all) {all.add(new ArrayList<>());for (Integer x : box) {all.get(all.size() - 1).add(x);}}void backTrace(int[] A,int start,List<Integer> box,List<List<Integer>> all) {final int N = A == null ? 0 : A.length;append(box, all);if (start >= N) {return;}for (int j = start; j < N; j++) {box.add(A[j]);backTrace(A, j + 1, box, all);box.remove(box.size() - 1);}}public List<List<Integer>> subsets(int[] A) {final int N = A == null ? 0 : A.length;List<Integer> box = new ArrayList<>();List<List<Integer>> ans = new ArrayList<>();backTrace(A, 0, box, ans);return ans;}
复杂度分析:时间复杂度,由于一共有 N 个元素,每个元素可能被放到子集中,也可能不被放到子集中,一共有 O(2N) 个子集,每个子集都需要一次遍历。假设都按最差情况处理,单个子集遍历时间复杂度为 O(N)。所以时间复杂度为 O(N* 2N)。不算上返回值 answer,那么空间复杂度为 O(N) 。
【小结】这个题目是一道非常经典的回溯的题目,下面我们分析一下考点:
- 回溯的模板
- 回溯代码的优化,即哪些变量可以被优化掉。
下面再和你多说两句。我发现,有时候会有小伙伴直接研究网络上已经优化过的代码,感觉自己看不懂回溯。这是两方面的原因导致的:
- 你没有真正理解到回溯的精髓;
- 网络上的很多代码都没有一步一步讲优化过程,还省略了很多关键步骤,最后直接给出答案。
这两个考点是你理解回溯代码的关键。因此,在看回溯代码的时候,一定要从模板出发,然后再通过优化得到最终的程序。
接下来我们通过一些练习来加强你对这个知识点的掌握。
练习题 2:在[1, 2, …, n] 这几个数中,选出 k 个数出来组成集合。输出所有的解。
输入:n = 2, k = 1
输出:[[1], [2]]
解释:一个数的选择只有 [1], [2]
练习题 3:给定一个正数数组 A[],和一个正整数 target。输出所有的子集,使得子集和等于 target。
注意:里面的元素可以重复选取。
输入:A = [2, 3, 8],target = 7
输出:[2, 2, 3]只有这个子集和等于 7。
练习题 4:给定一个正数数组 A[],和一个正整数 target。输出所有的子集,使得子集和等于 target。
注意:里面的元素不可以重复选取。
输入:A = [2, 3, 8], target = 5
输出:[2, 3] 只有这个子集和等于 5
这里,每个人的选项都是动态决定的,而不再像以前是固定选择 A[i],或者 A[i] 的某个固定的映射。可以做一个简单的小结:
第 i 个人的选项是动态决定的,可以认为是一个简单的函数 f(i) 来决定它的选项列表。
例 3:排列
【题目】给定无重复元素的数组,输出这个数组所有的排列。
输入:A = [1, 2]
输出:[[1, 2], [2, 1]]
解释:两个元素的数组的排列有两种。
【分析】输出数组的所有排列,看到 “所有” 二字,你应该条件反射知道这里需要用到回溯算法了。
注:排列算法的标准答案实际上没有几行,但却是经过很多优化步骤精简得到的,下面我们将从最原始的代码开始一步一步推导优化。
1. 1 个核心
首先看一下第 i 个人应该怎么选?比如:对于数组 [1, 2, 3] 而言,第 1 个人可以选择所有的元素。
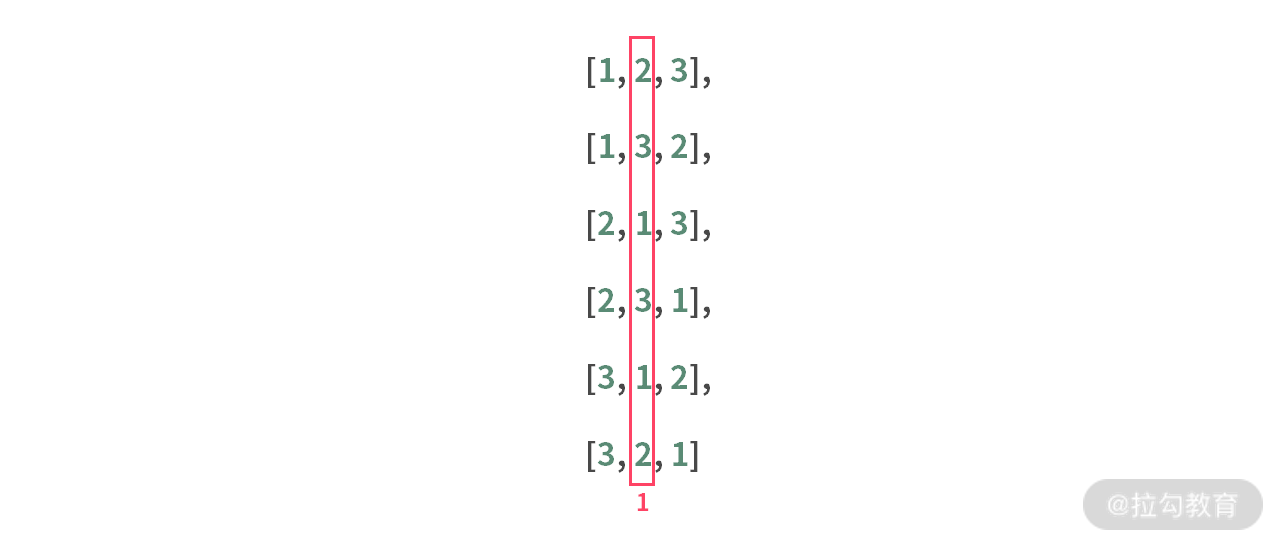
实际上,排列时,对于位置 i 来说,每个元素都是有可能出现的。因此,我们可以得到结论 2:
第 i 个人的选择范围是 [0, N)
此外,根据排列的性质,已经放到 box 中的元素不能再被第 i 个人选中。这样就得到了结论 3:
已经放到 box 中的元素,不能再被第 i 个人选中
2. 3 个条件
在使用回溯模板时,首先要想到的是回答回溯的 3 个条件。
- 满足的状态:一个排列成功之后,其长度应该是与原数组的长度一样,所以我们需要 box 的长度与输入的数组长度一样。
- 何时返回?一共有 N 个元素,每个人只能选一个放到排列中。从第 0 个人到第 N-1 个人都有元素可以选,第 [N, +inf) 个人都不会有元素可以选。
- 第 i 个人可以选的元素,需要满足结论 2 和结论 3。
我们可以写出伪代码如下(解析在注释里):
void backtrace(int[] A,int i,List<Integer> box,List<List<Integer>> ans) {final int N = A == null ? 0 : A.length;if (box.size() == N) {append(box, ans);}if (i >= N) {return;}for (int i = 0; i < N; i++) {if (!box.contains(A[i])) {box.add(A[i]);backtrace(A, i + 1, box, ans);box.remove(box.size() - 1);}}}
不过很快可以发现,box.contains() 函数是一个线性搜索复杂度,会导致整个算法的复杂度较高。这里我们可以使用一个哈希 /used[] 数组来记录这个元素是否被使用,就可以得到优化。
【代码】经过优化,可以得到第一个版本的代码如下(解析在注释里):
class Solution {private void append(List<Integer> box,List<List<Integer>> ans) {ans.add(new ArrayList<>());for (Integer x : box) {ans.get(ans.size() - 1).add(x);}}private void backtrace(int[] A,int i,boolean[] used,List<Integer> box,List<List<Integer>> ans) {final int N = A == null ? 0 : A.length;if (box.size() == N) {append(box, ans);}if (i >= N) {return;}for (int j = 0; j < N; j++) {if (!used[j]) {box.add(A[j]);used[j] = true;backtrace(A, i + 1, used, box, ans);box.remove(box.size() - 1);used[j] = false;}}}public List<List<Integer>> permute(int[] A) {final int N = A == null ? 0 : A.length;List<List<Integer>> ans = new ArrayList<>();if (N == 0) {return ans;}boolean[] used = new boolean[N];List<Integer> box = new ArrayList<>();backtrace(A, 0, used, box, ans);return ans;}}
复杂度分析:根据数学公式,我们知道一共会生成 N! 个结果,所以时间复杂度为 O(N!)。如果不算上输出空间,那么空间复杂度就是 O(N)。
我们会发现,基于 used[] 数组在扫描的时候,仍然会从头扫描到尾,那么有没有什么办法可以避免这种扫描呢?
这里我们再看一下第 i 个人的选择。假设第 i 个人将 “宝石” 放到箱子里之前,他身上有一个袋子,里面装着将要放到箱子里的宝石。
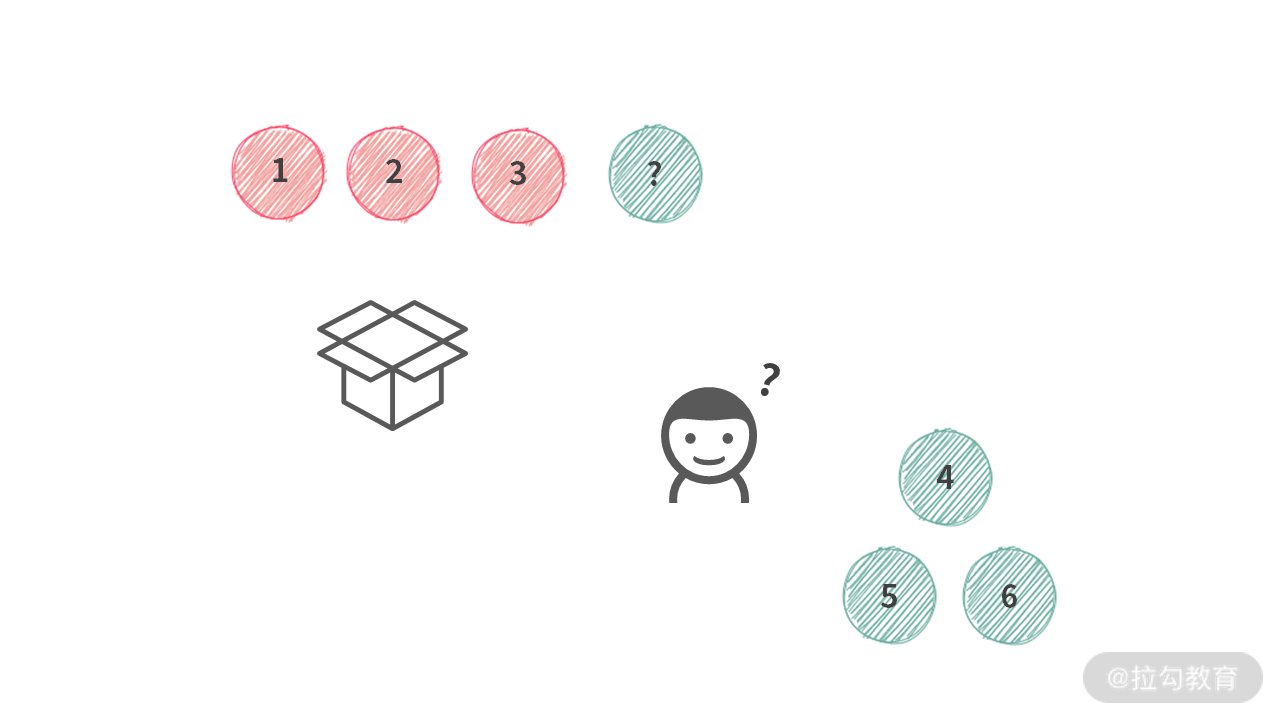
然后,我们重新再看 1 个核心和 3 个条件。
1. 1 个核心
根据核心的定义:重点解决第 i 个人应该选什么?我们从下面这种情况展开。
- 整个数组为 [1, 2, 3, 4, 5, 6]
- 已经有 [1, 2, 3] 元素在箱子里面
根据结论 2 和结论 3,容易得到,第 i 个人实际上只能选择 [4, 5, 6]。那么在操作时,第 i 个人可以像下图演示的这样操作。
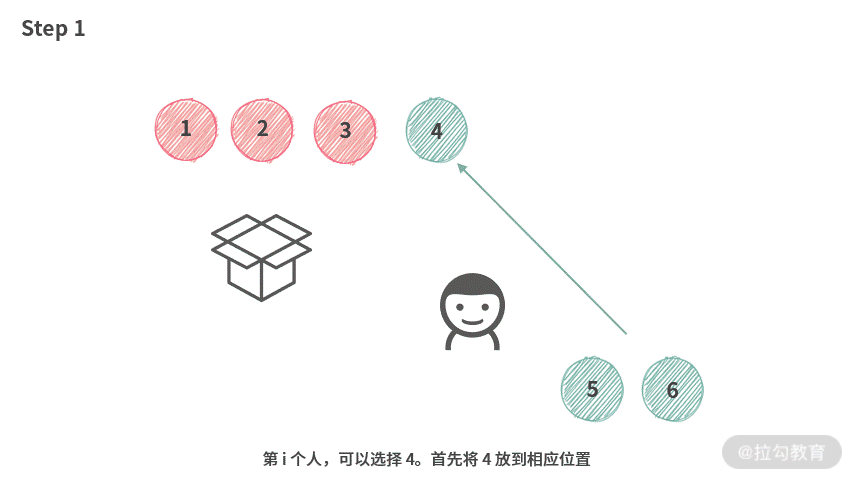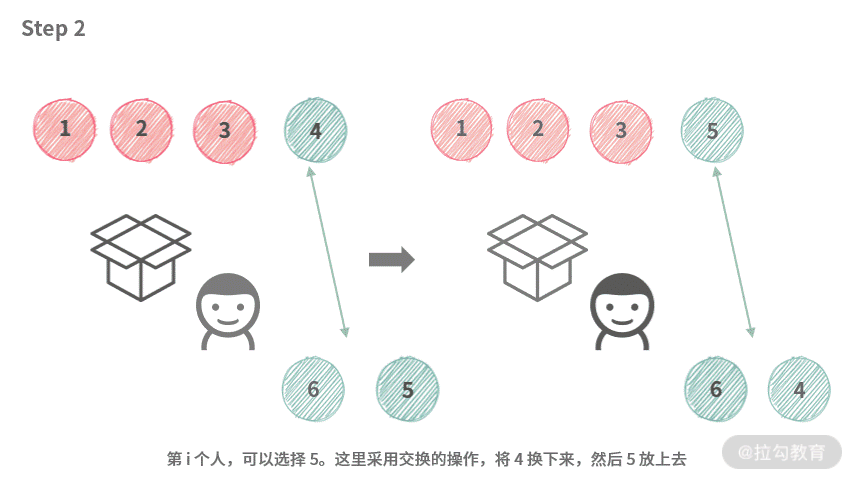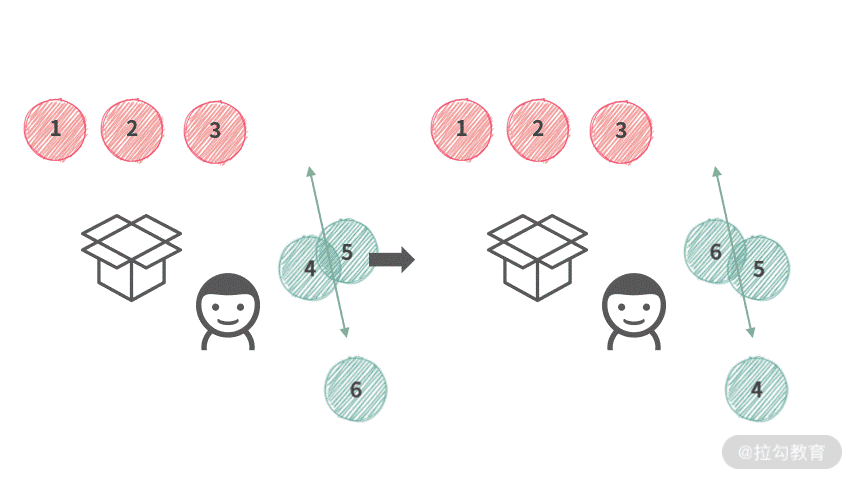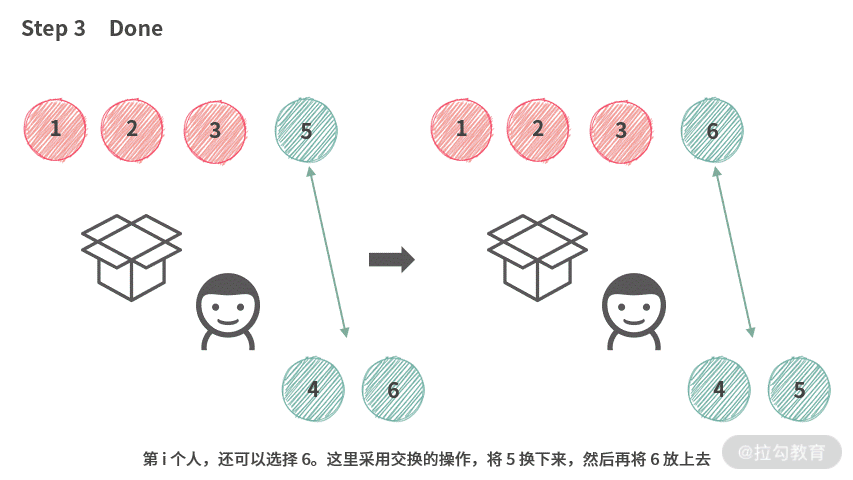
虽然,我们还没有找到一个较好的数据结构来实现袋子。但是,根据这里的操作,可以分析出只需要这种数据结构支持交换操作就可以了。
这时候,数组跳出来说:“正是在下”。我们在操作的时候,统一使用 Swap 操作,如下动图所示:
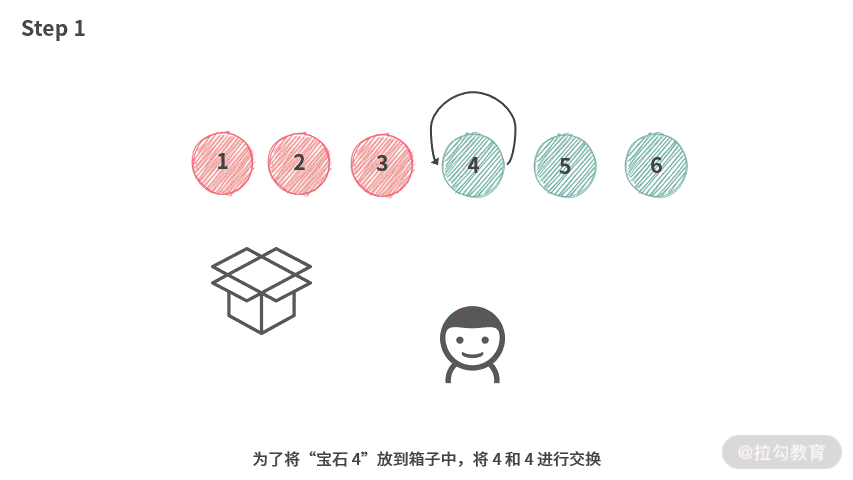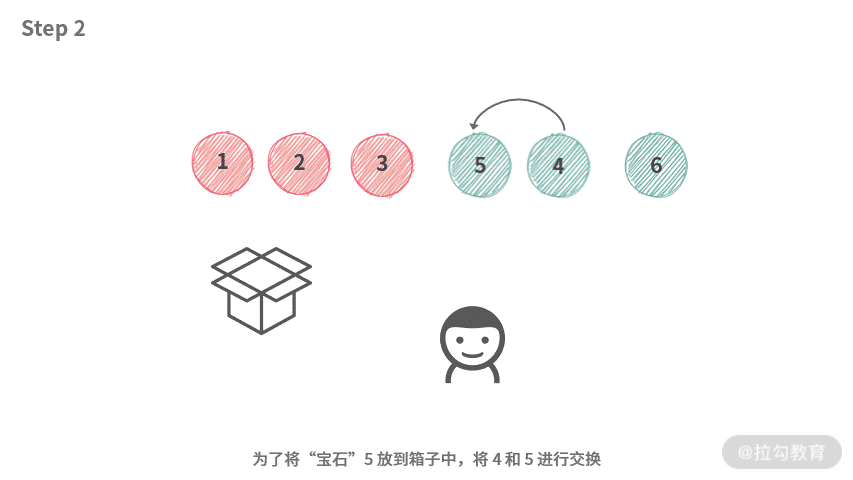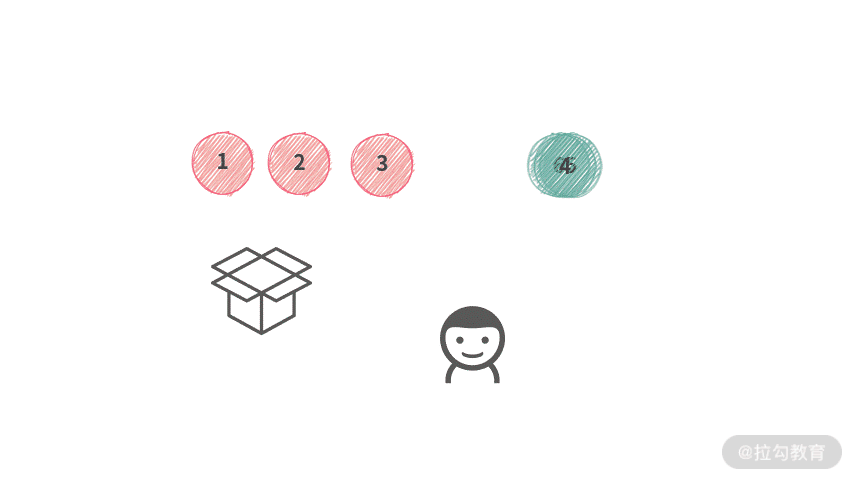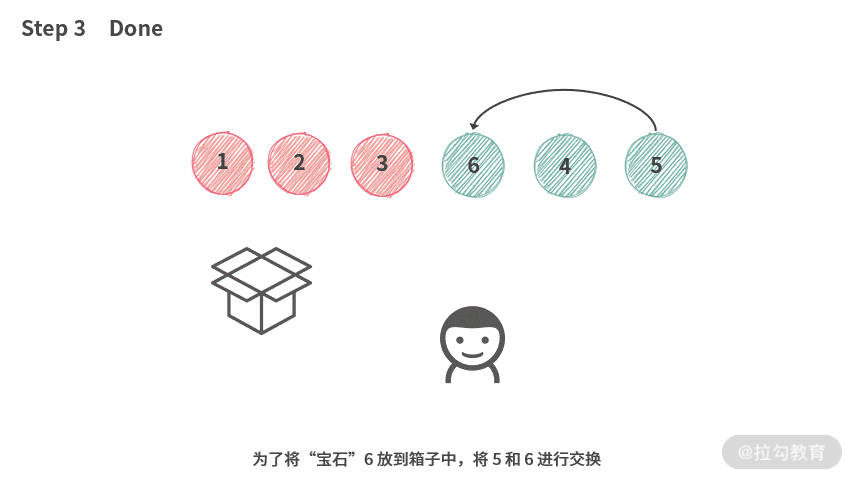
为了方便,第 i 个人实际上没有必要自己随身带着一个数组作为 “袋子”。只需要:
- 在箱子里提前放好可供选择的元素;
- 告知第 i 个人可以选择的元素的范围,在这里为 [i, N);
- 第 i 个人每次用完箱子之后,仍然要保证能将 “箱子” 恢复原样。
【代码 2】经过上述分析,我们可以得到第二个版本的代码(解析在注释里):
class Solution {private void append(int[] box, List<List<Integer>> ans) {ans.add(new ArrayList<>());for (int x: box) {ans.get(ans.size()-1).add(x);}}private void swap(int[] box, int a, int b) {int t = box[a];box[a] = box[b];box[b] = t;}private void backtrace(int[] A,int i,int [] box,List<List<Integer>> ans){final int N = A == null ? 0 : A.length;if (i == N) {append(box, ans);}if (i >= N) {return;}for (int j = i; j < N; j++) {swap(box, i, j);backtrace(A, i + 1, box, ans);swap(box, i, j);}}public List<List<Integer>> permute(int[] A) {final int N = A == null ? 0 : A.length;List<List<Integer>> ans = new ArrayList<>();if (N == 0) {return ans;}int[] box = new int[N];for (int i = 0; i < N; i++) {box[i] = A[i];}backtrace(A, 0, box, ans);return ans;}}
复杂度分析:根据数学公式,我们知道一共会生成 N! 个结果,所以时间复杂度为 O(N!)。如果不算上输出空间,那么空间复杂度就是 O(N)。
这里我们发现,box 的状态实际上分为了两部分:一是可选部分,二是不可选部分。
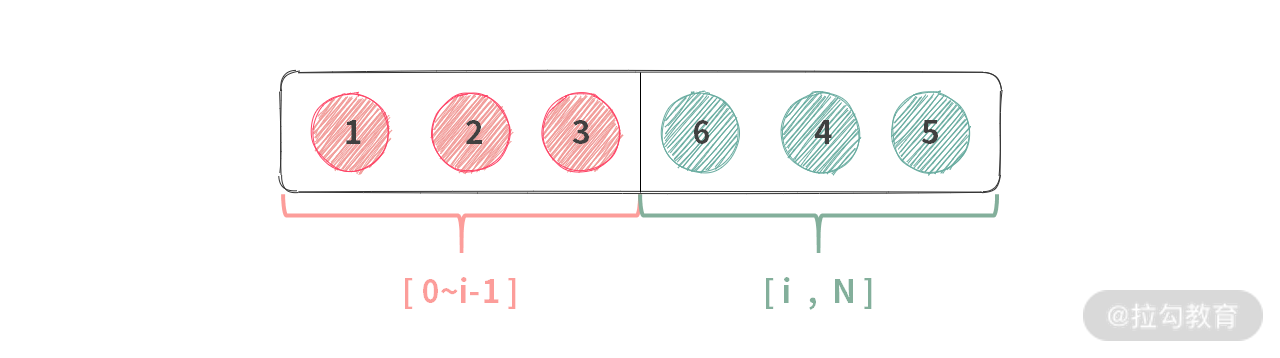
此时的 “箱子” 使用了数组,不再像以前那样只管 push/pop,还需要记录状态:
- 需要填 box 的哪个位置?
- 第 i 个人可以选择的范围是哪里?
原本函数需要声明为:
private void backtrace(int[] A,int boxId,int i,int start,int end,int [] box,List<List<Integer>> ans)
不过这里巧的是:
- boxId 刚好等于 i
- start 也刚好是 i
- end 一直都是 N
所以代码也就可以优化成上面的样子。如果我们再研究一下,可以发现一些新的东西,如下所示:
public List<List<Integer>> permute(int[] A) {final int N = A == null ? 0 : A.length;int[] box = new int[N]; <-- 这里复制了数组Afor (int i = 0; i < N; i++) {box[i] = A[i];}backtrace(A, 0, box, ans);assert box == A;return ans;}
根据上述代码不难发现,实际上没有必要使用 box 数组,直接使用 A[] 数组就可以了。
【代码】因此,最终版本的代码如下(解析在注释里):
class Solution {private void append(int[] box, List<List<Integer>> ans) {ans.add(new ArrayList<>());for (int x: box) {ans.get(ans.size()-1).add(x);}}private void swap(int[] box, int a, int b) {int t = box[a];box[a] = box[b];box[b] = t;}private void backtrace(int[] box,int i,List<List<Integer>> ans){final int N = box == null ? 0 : box.length;if (i == N) {append(box, ans);}if (i >= N) {return;}for (int j = i; j < N; j++) {swap(box, i, j);backtrace(box, i + 1, ans);swap(box, i, j);}}public List<List<Integer>> permute(int[] A){final int N = A == null ? 0 : A.length;List<List<Integer>> ans = new ArrayList<>();if (N == 0) {return ans;}backtrace(A, 0, ans);return ans;}}
复杂度分析:时间复杂度 O(N!),如果不算返回值占用的空间,那么空间复杂度为 O(N)(因为递归栈也会占用空间)。
【小结】在这个题里面,我们采用了层层优化的方法给你讲解最终代码的由来。虽然核心代码非常短,但是其意义很丰富。
我们再回顾一下推导过程,如下图所示:
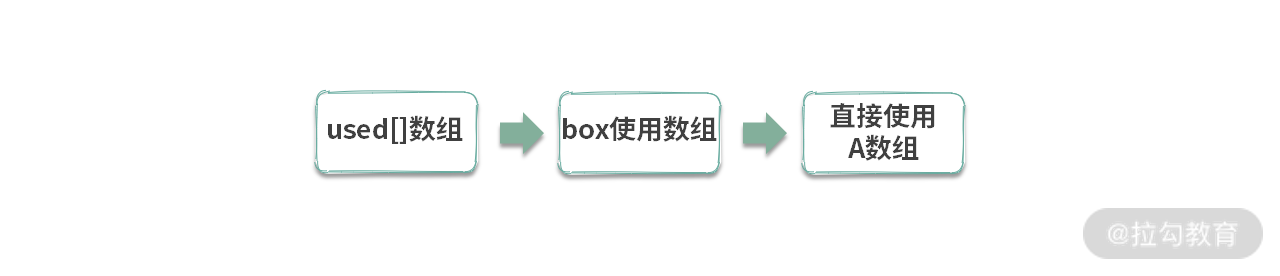
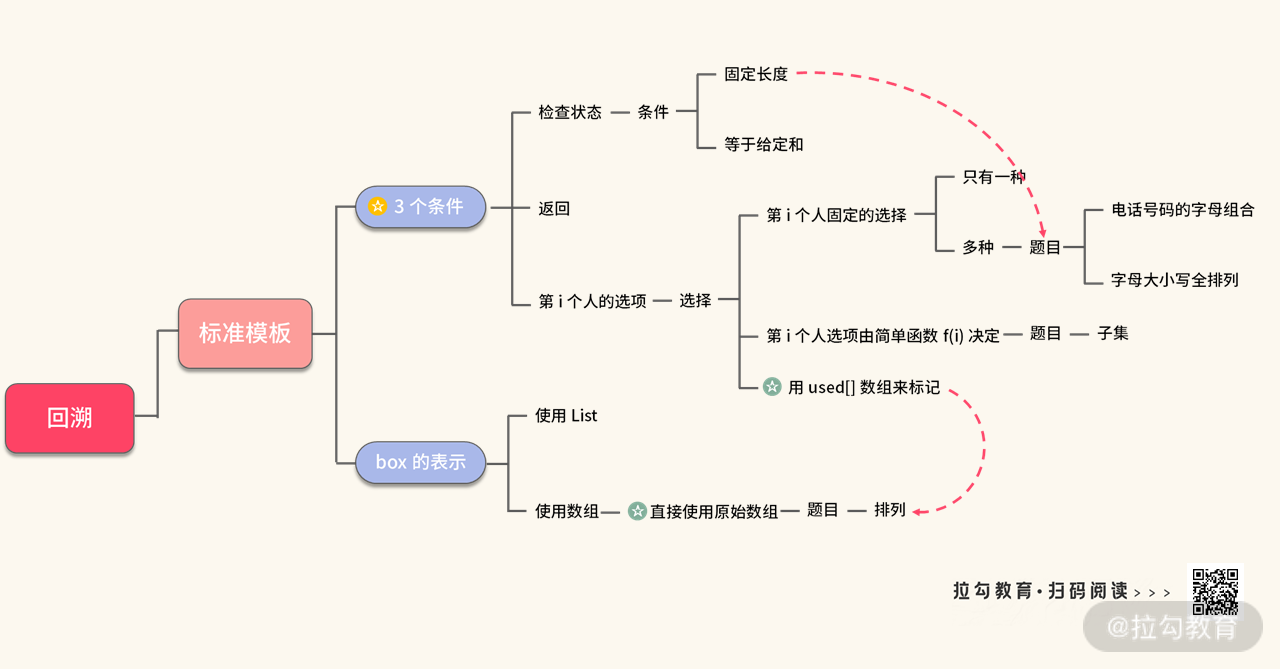
到这里,我们可以将回溯的知识点总结如下:
去重排列组合
在排列组合问题中,另外一类问题是带有重复元素,并且需要去重处理。在处理这些问题的时候,除了套用前面所讲的回溯模板之外,还需要注意使用以下两步来进行去重。
- 排序:因为排序可以将相同的元素放到一起。
- 查重:通过查看已有的元素是否已经被使用,进而去重。
例 4:子集 2
【题目】给定一个可能包含重复元素的整数数组 A,返回该数组所有可能的子集。注意:解集不能包含重复的子集。
输入:A = [1, 2, 2]
输出:[[2], [1], [1,2,2], [2,2], [1,2],[]]
解释:注意:虽然 {A[0]=1, A[1]=2}, {A[0]=1, A[2]=2} 是选取不同位置的数,但是却都构成了 {1,2} 这个子集,因此,只能算一个。
【分析】你又看到了 “所有” 两个字,那么就可以确定使用回溯算法了。如果回顾一下例 2 讲解的关于子集的问题,我们会发现,这里可以使用结论 1(由例 2 得来)。
如果第 i 个人选择了 A[j],那么第 i+1 个人的选择范围就是 A[j + 1, N)
本质上是因为例 2 中已经说明 A[] 数组中没有相同的元素。那么在本题中,如果有相同的元素应该如何处理?
老规矩,我们还是从 1 个核心开始思考这个问题。
1. 1 个核心
我们把思路的核心放在第 i 个人的选择上。对于第 i 个人来说,如果我们依然使用(例 2 的)结论 1:
如果第 i 个人选择了 A[j],那么第 i+1 个人的选择范围就是 A[j + 1, N)
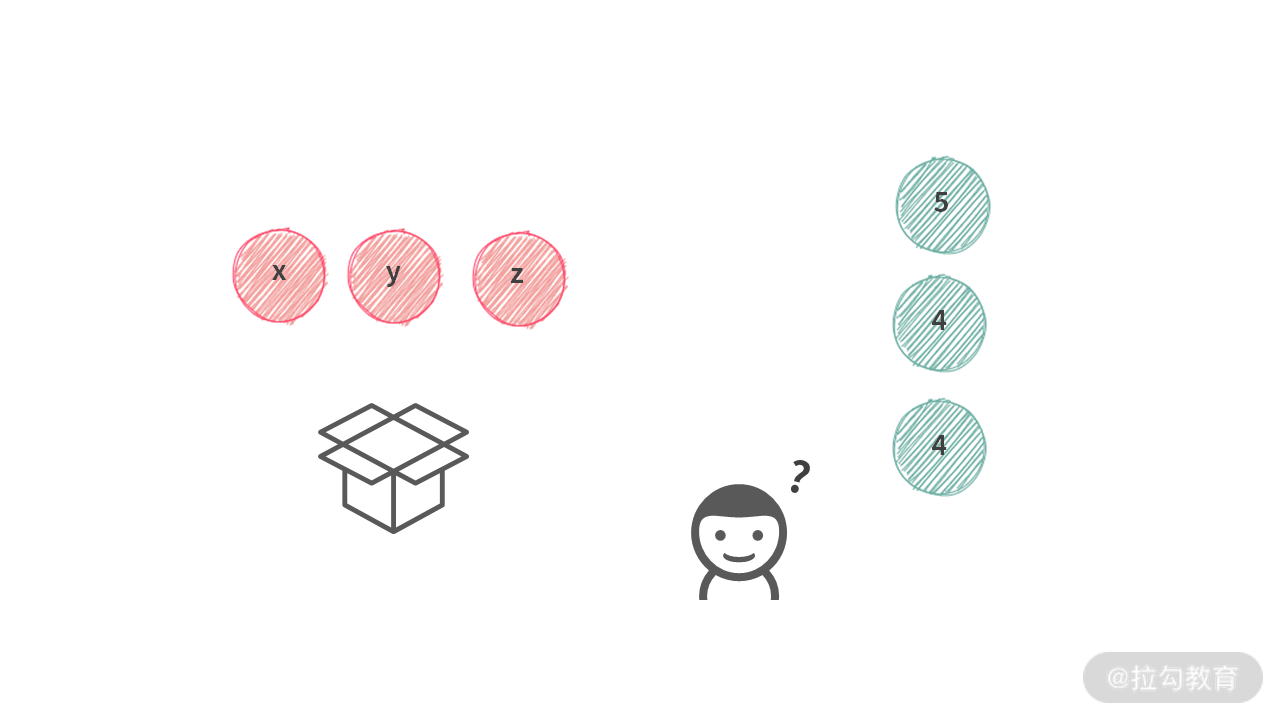
对于这种情况,在回溯时,实际上会出现重复。伪代码如下(为了让你看得更加清楚,这里没有使用 for 循环):
void backtrace(int[] A, int i, Box s) {final int N = A == null ? 0 : A.length;s.print();if (i >= N) {return;}s.push(第i个人的宝石5);backtrace(A, i + 1, s);s.pop();s.push(第i个人的宝石4);backtrace(A, i + 1, s);s.pop();s.push(第i个人的宝石4);backtrace(A, i + 1, s);s.pop()}
我们会发现,后面的宝石 4 实际上是重复的。因为题目要求:不同位置上的同值元素会被认为是一样的。因此,我们要想办法做去重。
去重方法 1:你可以这样理解。你的左裤兜里面有个红宝石,右裤兜里面有个一样的红宝石。每次你都只能往箱子里放一个宝石(并且是放在箱子里面同样的位置),给你的朋友嘚瑟。
你朋友肯定会问:“你为什么要把同样的东西给我看两遍?”。
这时,你只需要对第 i 个人去重就可以了。那么我们很快就可以写出如下的伪代码:
void backtrace(int[] A, int i, Box s) {final int N = A == null ? 0 : A.length;s.print();if (i >= N) {return;}S = HashSet();for 宝石 in {第i个人当前所有宝石选项} {if (!S.contains(宝石)) {s.push(宝石);backtrace(A, i + 1, s, answer);s.pop();S.add(宝石);}}}
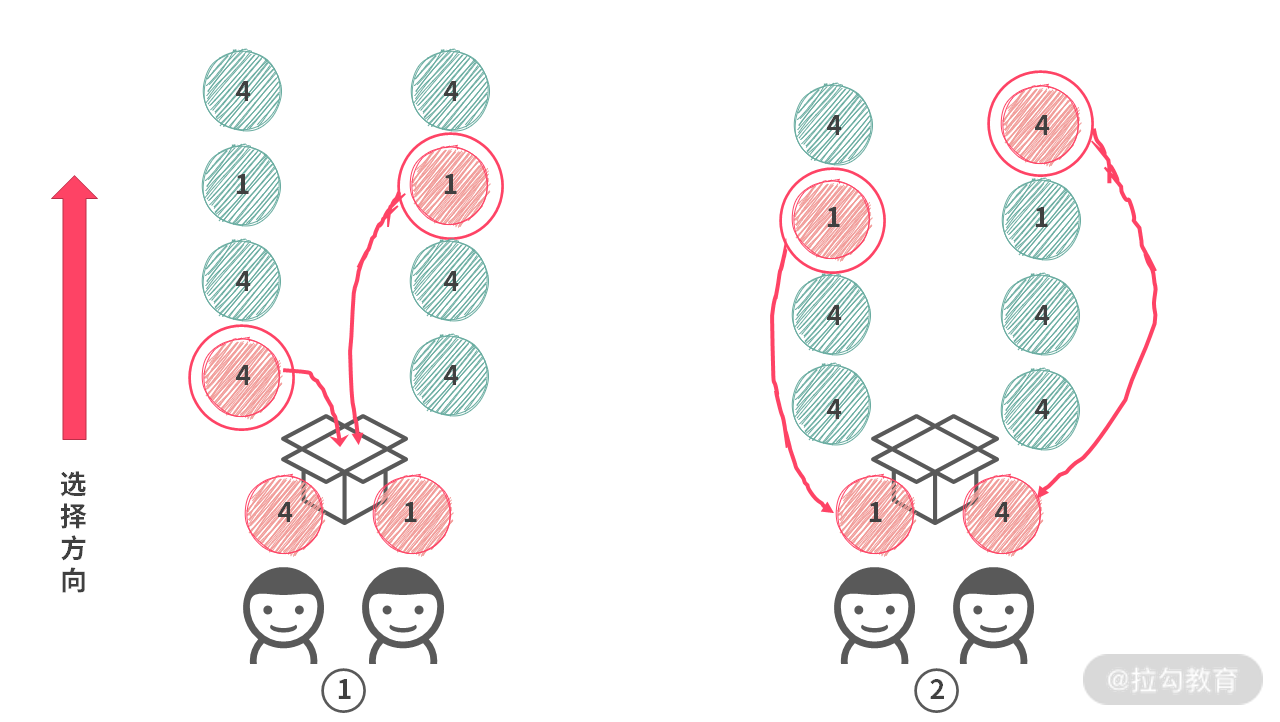
但是,如果只是对第 i 个人去重,还会遇到一个问题。比如:数组为 A = [4, 4, 4, 1, 4],假设只有两个人在选择的时候,下图所示的 ① ② 两种情况就有可能出现重复。
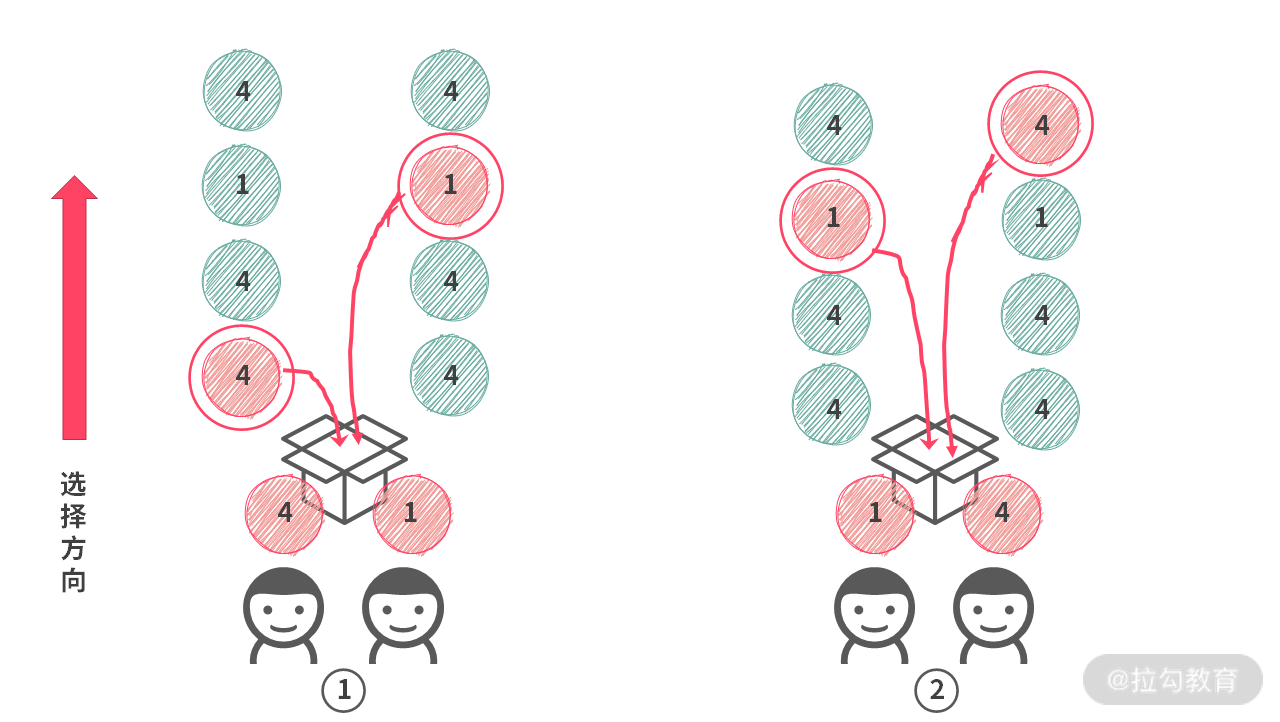
那么如何避免这种 [1, 4] 和 [4, 1] 重复的情况呢?
去重方法 2:再看一下第 i 个人在选择范围上的(例 2 的)结论 1:
如果第 i 个人选择了 A[j],那么第 i+1 个人的选择范围就是 A[j + 1, N)
为了方便讨论问题的本质,在只有两个人的情况下,结论 1 由递归可以很容易展开成循环的情况(用循环描述起来更容易)。
for (int j = start; j < end; j++):for (int jj = j + 1; jj < end; jj++):{A[j], A[jj]} -> 放到结果子集
若 A[] 数组中没有相同元素的进来,这样循环就不会产生相同子集。但是,如果有相同元素进来,我们需要将数组排序之后再进行处理:
sort(A);for (int j = start; j < end; j++):for (int jj = j + 1; jj < end; jj++):{A[j], A[jj]} -> 放到结果子集
如果对于 A[] = [1, 4, 4, 4] 而言(已经排序了),那么子集合中就只能出现 [1, 4],而不会再出现 [4, 1]。因为下面这个结论 4 是可以证明的:
从一个有序数组中,选择一个子序列出来,这个子序列必然是有序的。
关于结论 4 ,我希望你可以尝试证明一下,也欢迎你把证明过程写在评论区,我们一起交流。我们回到题目中来,如果只排序,只能保证 [1, 4] 和 [4, 1] 两个子集不会重复,并不能避免 [1, A[1] = 4] 和 [1, A[2] = 4] 这种类型的重复。
看来是时候将去重方法 1和去重方法 2 合体了。变身吧!
最终解:再加 hash_set,就可以避免重复子集了,代码如下所示(解析在注释里):
sort(A);i_set = HashSet;for (int j = start; j < end; j++) {if (i_set.contains(A[j])) continuei1_set = HashSet;for (int jj = j + 1; jj < end; jj++) {if (i1_set.contains(A[jj])) continue;{A[j], A[jj]} -> 放到结果子集}}
下面我们再来看一道练习题。
练习题 5:给定一个排序后的数组,去除里面的重复元素,求返回去重后数组的长度。
如果你做过这个题,就会发现,在排序后的数组处理去重的时候,只需要和前面的元素进行比较就可以了。
2. 3 个条件
接下来,我们再看回溯的 3 个条件。
1)满足的状态:由于我们已经通过排序 + 前面的元素进行比较,进行了去重,因此,只需要把状态放到结果中就可以。
2)何时返回?一共有 N 个元素,每个人只能选一个放到组合中。从第 0 个人到第 N-1 个人都有元素可以选,第 [N, +inf) 个人都不会有元素可以选。
3)第 i 个人可以选的元素,需要满足结论 1,并且需要利用有序性来去重。
【代码】那么到这里为止,我们已经可以写出代码了(解析在注释里):
class Solution {private void append(List<Integer> box,List<List<Integer>> ans) {ans.add(new ArrayList<>());for (Integer x : box) {ans.get(ans.size() - 1).add(x);}}private void backtrace(int[] A,int start,List<Integer> box,List<List<Integer>> ans){final int N = A == null ? 0 : A.length;append(box, ans);if (start >= N) {return;}for (int j = start; j < N; j++) {if (j > start && A[j] == A[j-1]) continue;box.add(A[j]);backtrace(A, j + 1, box, ans);box.remove(box.size()-1);}}public List<List<Integer>> subsetsWithDup(int[] A) {final int N = A == null ? 0 : A.length;List<Integer> box = new ArrayList<>();List<List<Integer>> ans = new ArrayList<>();if (N <= 0) {return ans;}Arrays.sort(A);backtrace(A, 0, box, ans);return ans;}}
复杂度分析:时间复杂度为 O(N x 2N),如果不算返回值占用的空间,空间复杂度为 O(N)。
【小结】在这里,我们步步为营,重点分析了第 i 个人应该做的选择项,最后利用排序之后子序列无重复的特性进行了去重处理。
这里我给出推导过程中的每一步的代码,供你参考。
第一步,使用排序 + Set。
第二步,使用排序 + 和前面的元素进行比较而去重。
第三步:利用例 2 的精简参数的办法,对第二步的代码进行 “瘦身”。
例 5:排列 2
【题目】给定一个可包含重复数字的数组 A ,按任意顺序返回所有不重复的全排列。
输入:A[] = [1, 1, 2]
输出:[[1,1,2], [1,2,1], [2,1,1]]
解释:[A[0], A[1], A[2]] 与 [A[1], A[0], A[2]] 是一个重复的排列,不能放在其中。其他重复的排列也类似。因此最终只有 3 个数组有排列。
【分析】这个题与例 3 的区别在于:数组 A[] 可能包含重复数字的。我们还是先从 1 个核心开始分析。
1. 1 个核心
根据例 3 的分析,当第 i 个人的选择范围是余下的 {4, 7, 4, ,4} 的时候,他可以进行的操作是不停地交换。
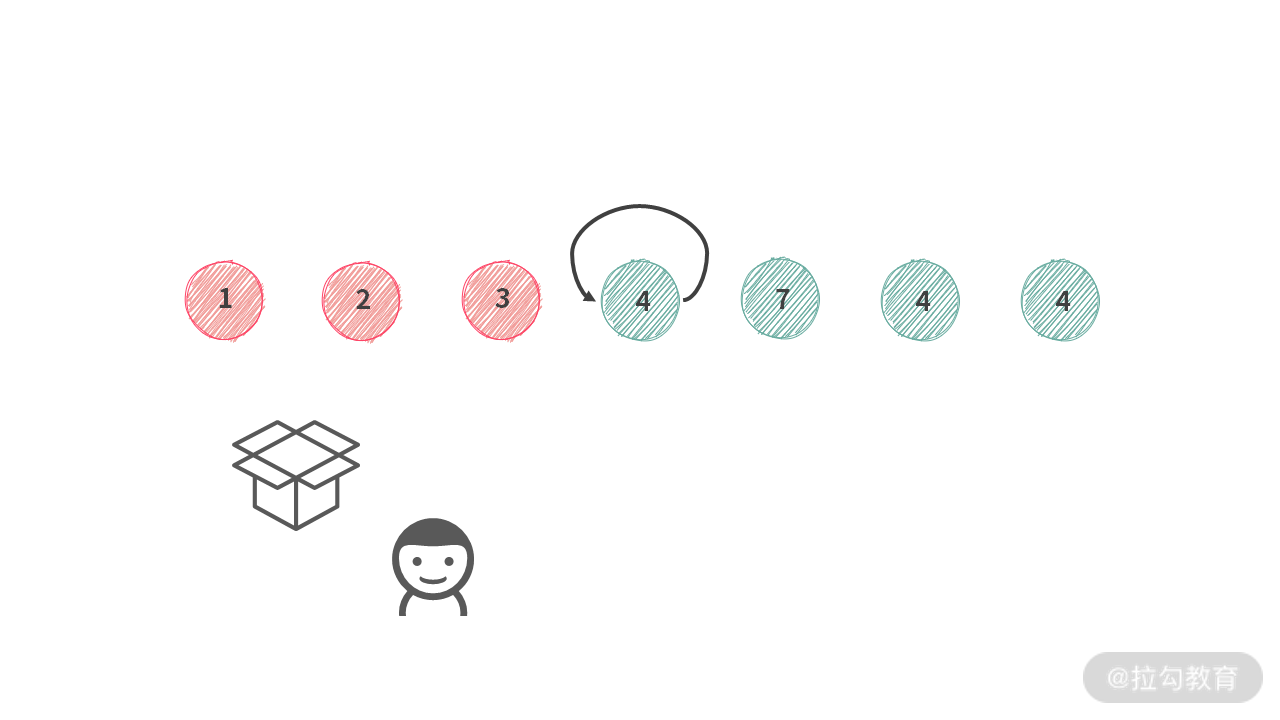
但是,当遇到下面这种场景时,可以发现,交换带来的结果是一样的:
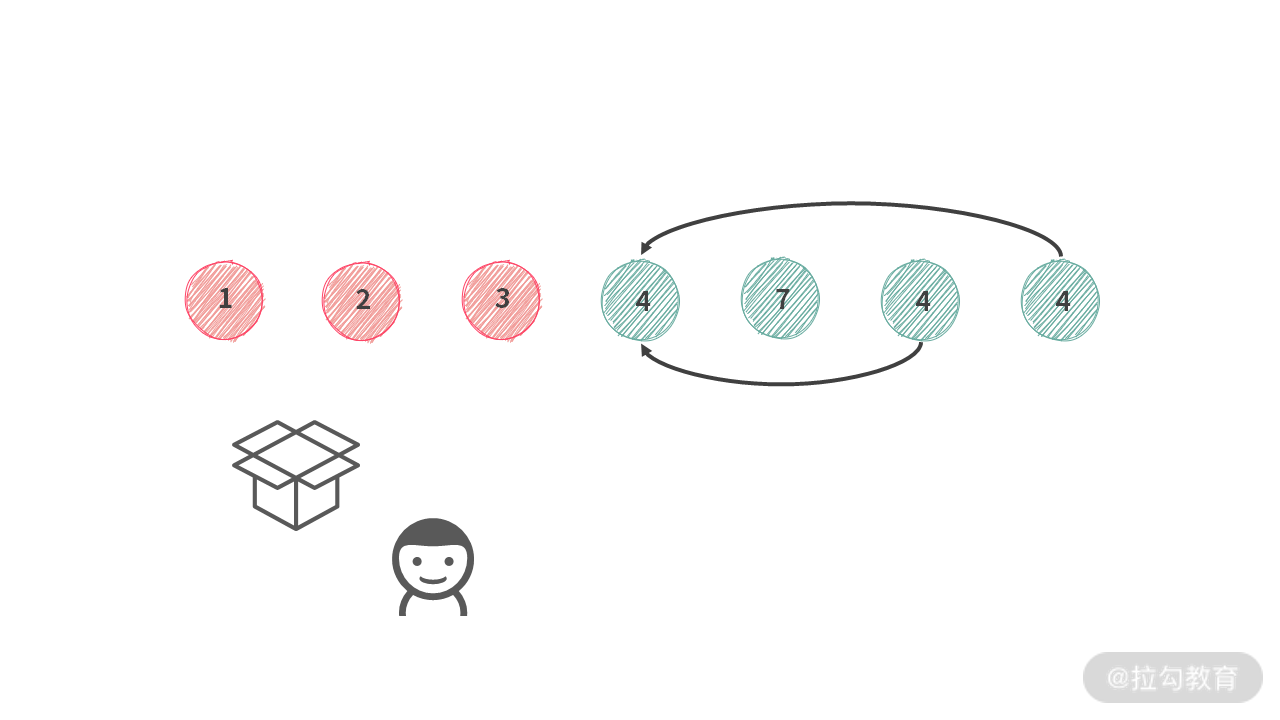
因此,需要去重。从第 i 个人的视角出发,我们可以发现,由于执行的是 Swap 操作,实际上没有必要重复地把一个相同值的元素放到 box 中同样的位置。
具体来说,我们可以采用哈希记录的办法来去重。在例 3 的基础上,修改代码如下(解析在注释里):
private void backtrace(int[] box,int start,List<List<Integer>> ans){final int N = box == null ? 0 : box.length;if (start == N) {append(box, ans);return;}Set<Integer> s = new HashSet<>();for (int j = start; j < N; j++) {if (!s.contains(box[j])) {swap(box, start, j);backtrace(box, start + 1, ans);swap(box, start, j);s.add(box[j]);}}}
不过,我们在例 4 中,提到过一种重复的情况,比如下图展示等情况:
为什么在这里不需要处理?因为在本题中,我们需要求解的是排列,而 [1, 4] 和 [4, 1] 本来就是不一样的,所以不需要处理这种情况。
这里我们使用了 HashSet,虽然它的复杂度是 O(1),但是在数据量比较小的时候,直接基于线性查找的方式可能会更快一些。主要基于以下两点:
- HashSet 需要动态申请和释放内存,代价比较大;
- 线性查找具有较好的内存局部性,对 CPU 的缓存更加友好。
因此,我们可以使用线性查找的方式来确定将要交换的元素在之前是否出现过了。
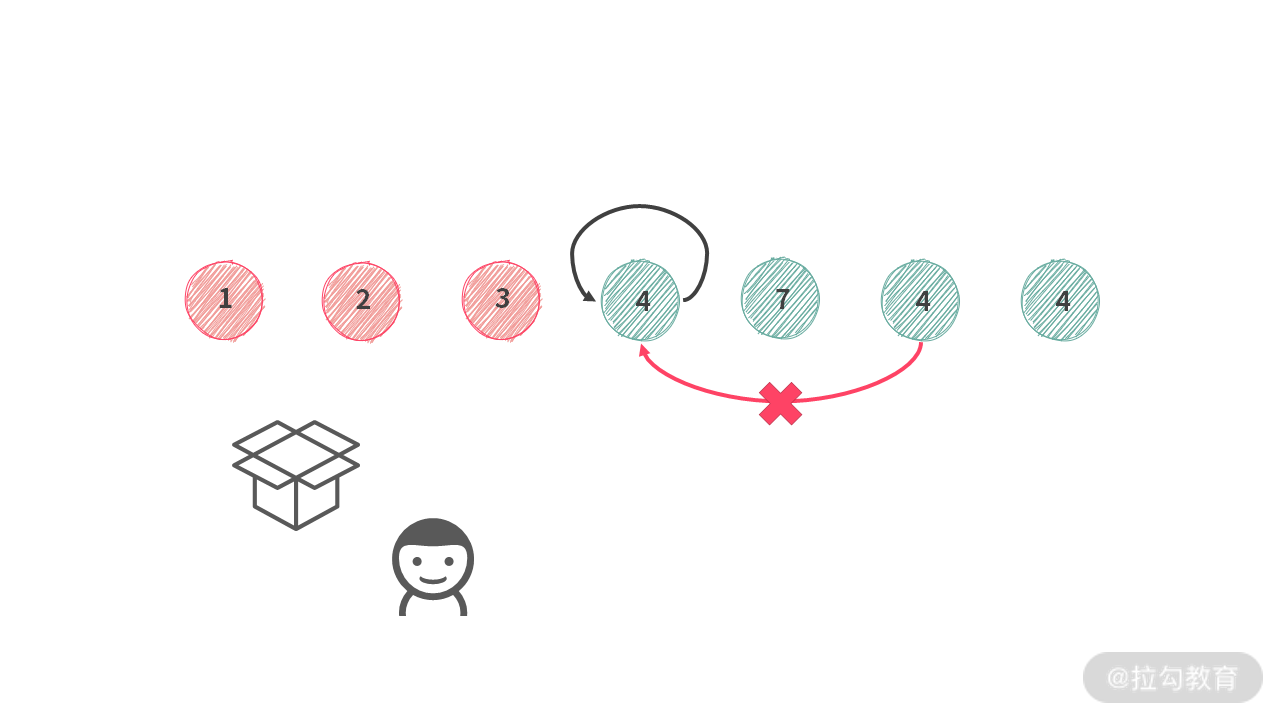
由于第 i 个人只需要执行 Swap 操作,那么,当前面已经将 4 放到 box[start],后面的 box[j] = 4 就没有必要再执行 Swap 操作,将 4 放到 box[start] 里了。
所以,除了用哈希处理,我们还可以直接利用线性查找这一操作:
for (int k = start; k < j; k++) {if (box[k] == A[j]) {}}
2. 3 个条件
经过前面的洗礼,想必你对于三个条件的分析已经非常明白了,下面我们再总结一下。
- 满足的状态:一个排列成功之后,其长度应该与原数组的长度一样。所以我们需要 box 的长度与输入的数组长度一样。
- 何时返回?一共有 N 个元素,每个人只能选一个放到排列中。从第 0 个人到第 N-1 个人都有元素可以选,第 [N, +inf) 个人都不会有元素可以选。
- 第 i 个人可以选的元素,需要满足结论 2 和结论 3,并且还需要注意去重。
【代码】那么最终代码可以如下(解析在注释里):
class Solution{private void append(int[] box, List<List<Integer>> ans) {ans.add(new ArrayList<>());for (Integer x : box) {ans.get(ans.size() - 1).add(x);}}private void swap(int[] box, int i, int j) {int t = box[i];box[i] = box[j];box[j] = t;}private boolean find(int[] box, int start, int end, int val) {for (int i = start; i < end; i++) {if (box[i] == val) {return true;}}return false;}private void backtrace(int[] box,int start,List<List<Integer>> ans){final int N = box == null ? 0 : box.length;if (start == N) {append(box, ans);return;}for (int j = start; j < N; j++) {if (!find(box, start, j, box[j])) {swap(box, start, j);backtrace(box, start + 1, ans);swap(box, start, j);}}}public List<List<Integer>> permuteUnique(int[] A) {List<Integer> box = new ArrayList<>();List<List<Integer>> ans = new ArrayList<>();final int N = A == null ? 0 : A.length;if (N == 0) {return ans;}backtrace(A, 0, ans);return ans;}}
复杂度分析:最差情况下,假设每个数都不一样,一共有 O(N!) 种排列,每种排列需要 O(N) 来放到输出里面,所以时间复杂度为 O(N x N!)。如果不算返回值,那么空间复杂度就是 O(N)。
【小结】在排列的情况下,我们发现,实际上去重操作要简单一些,只需要保证第 i 个人不要重复地把相同的内容放到同一个位置就可以了。
以上,我们学习了两个子集问题,两个排列问题,下面我分别从两个维度去总结两个题目。
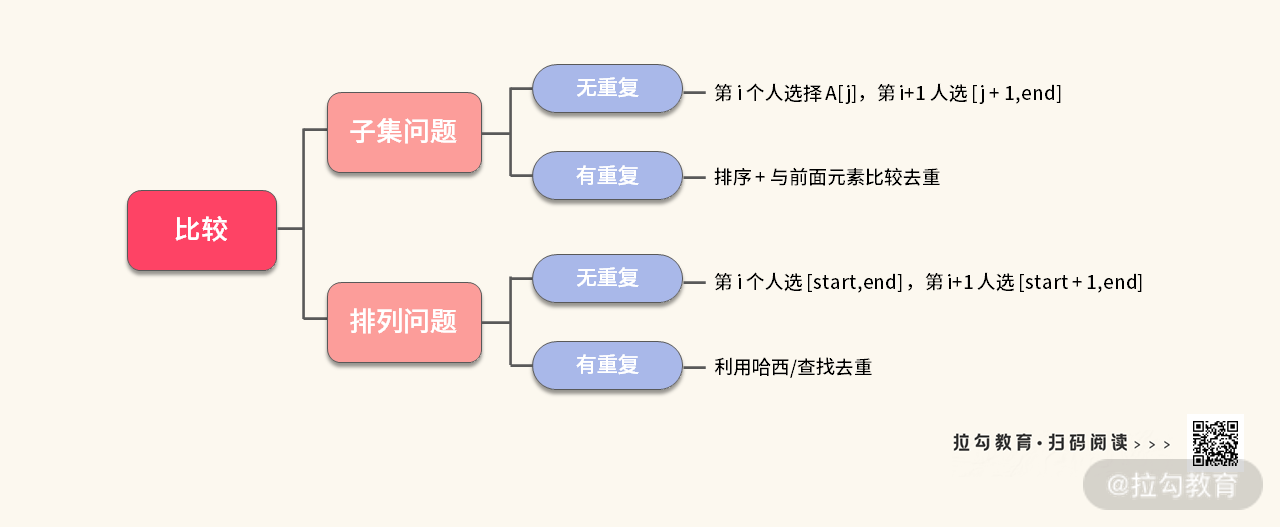
这里我再留一个思考题,检验一下你对子集和排列的理解是否到位。
思考题:在排列组合中,子集问题的递归函数的写法是:
backTrace(A, start, box, ans)|-> backTrace(A, j + 1, box, ans)
而排列问题的递归调用是:
backTrace(box, start, ans)|-> backTrace(A, start + 1, box, ans)
为什么一个是 j+1,一个是 start+1 呢?老规矩,你一定要自己操作一下,这样才能真正消化我给你讲解的知识和解题技巧。
总结
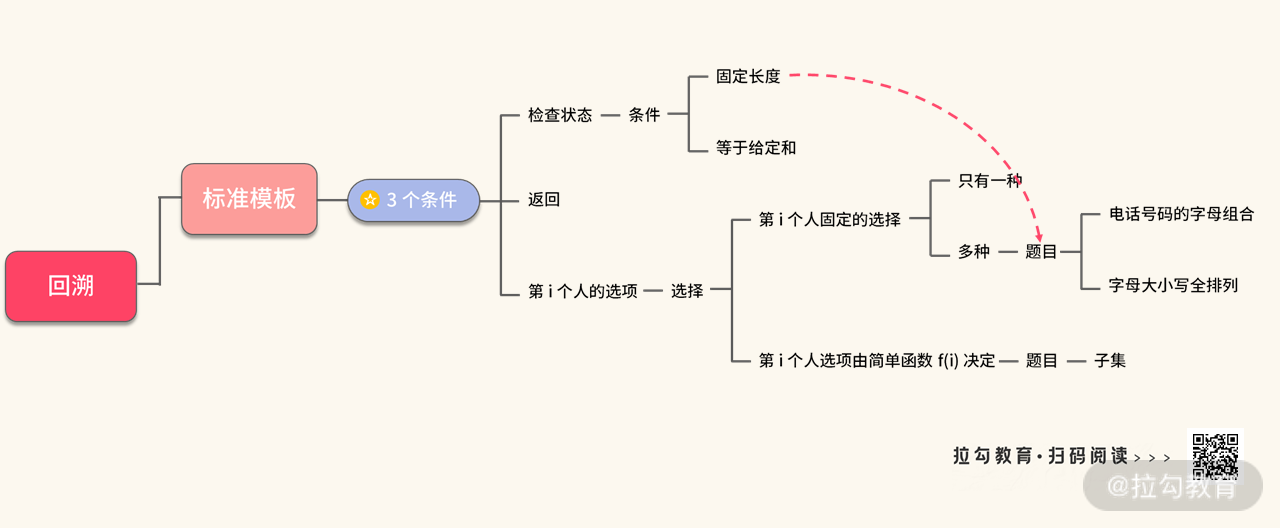
在本讲,我们介绍了回溯题目的 1 个模板、1 个核心,以及 3 个条件。选取了几道具有代表性的题目进行讲解,回溯的题目还有很多。不过只要你领会到本讲价绍的分析方法和解题思想,再遇到回溯问题就难不倒你了。另外,我再强调一句,在处理回溯问题时,还需要注意去重的处理,理解为什么要这样处理。
为了方便你复习,我把本讲重要的知识点总结在如下图所示的思维导图里,你可以利用课下时间进行消化,再结合练习题巩固今天所学的知识。
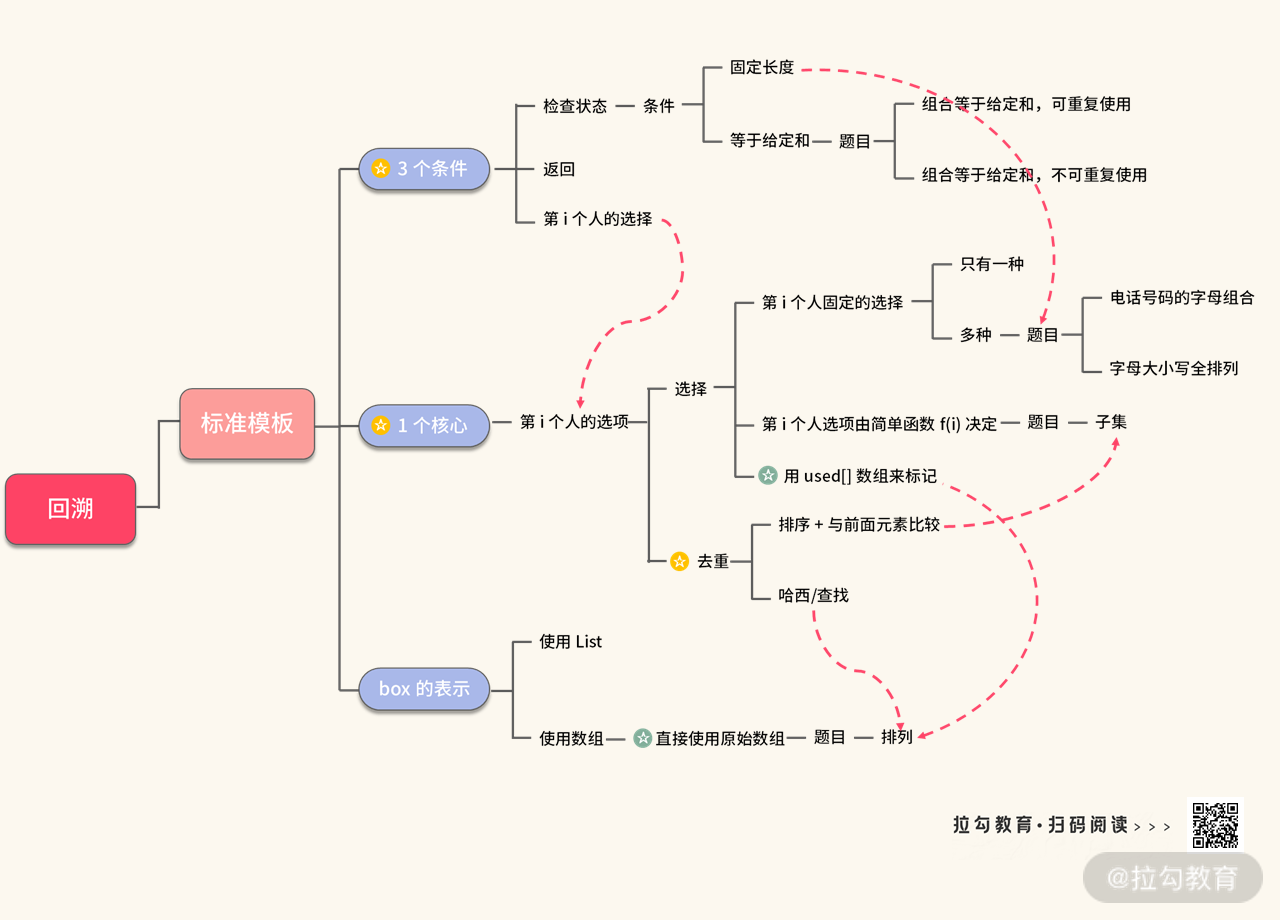
思考题
最后再给你留一个思考题。
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1~9 的正整数,并且每种组合中不存在重复的数字。
输入:n = 7, k = 3
输出:[1, 2, 4]
解释:只有 3 个数且和为 7 的组合为 [1, 2, 4]
关于回溯的知识我们就介绍到这里,接下来请和我一起踏上更加奇妙的算法旅程,下一讲将介绍:13 | 搜索:如何掌握 DFS 与 BFS 的解题套路?记得按时来探险。

