数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
本讲是一题多解模块的最后一讲,之所以安排这一讲,是因为通常情况下,一道算法题目有多种的解法。我们与别人交流时,大家的思路和解题方法可能不同,每个人写出来的代码差异巨大。那么这些不同的正确解法,可以理解成 “一题多解” 吗?换句话说,你能分清什么是真正的 “多解”,什么是“伪多解” 吗?
通过这些 “伪多解”,有助于我们看透题目的本质,从而掌握核心知识点,同时也可以降低我们需要理解和记忆的知识量。
所以,在本讲,你将掌握以下三种思考方法:
- 如何通过 “多解” 看透知识点的本质(分清“伪多解”“真多解”)?
- 如何用多种技巧满足题目要求?
- 如何深挖题目特点,达到一题多解的目标?
题目
给定一系列的会议,时间间隔 intervals,包括起始和结束时间[[s``1``,e1],[s``2``,e2],``...``]````(``s``i < ei),找到所需的最小的会议室数量。
输入:会议时间表 [[0, 30],[5, 10],[15, 20]]
输出:最少需要的会议室数量 2
注意:如果有两个会议 [6,8] 和 [8,10],我们认为这两个会议不冲突。
特点 1:时间分布
拿到这个题时,我们要特别注意一点:
如果有两个会议,其中一个会议结束于时间点 x,下一个会议同时从时间点 y 开始,这两个会议可以用同一个会议室。也就是说,这两个时间段并不重合(虽然在时间点 x 相接)。
我们从时间点出发来考虑这个问题,有以下 3 种情况。
情况 1:需 1 个会议室
首先我们考虑一种简单的情况,假设会议与会议之间均没有重合的情况。比如输入如下:
intervals=[0,1],[1,2],[2, 3]
在下图中,x 轴表示会议的时间表,y 轴表示将哪些会议放在哪个会议室,蓝色、橘色和红色分别表示不同的会议。
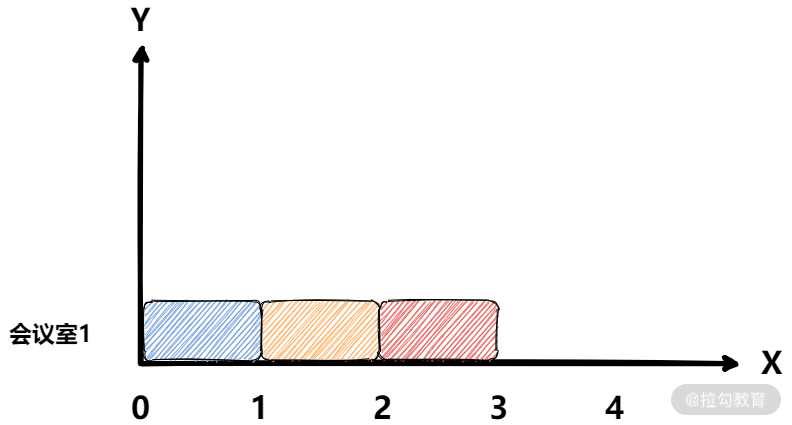
在这种情况下,每个时间点只可以被染上一种颜色,时间衔接得非常好,此时只需要一个会议室。接下来我们再看一下衔接得不那么好的情况。
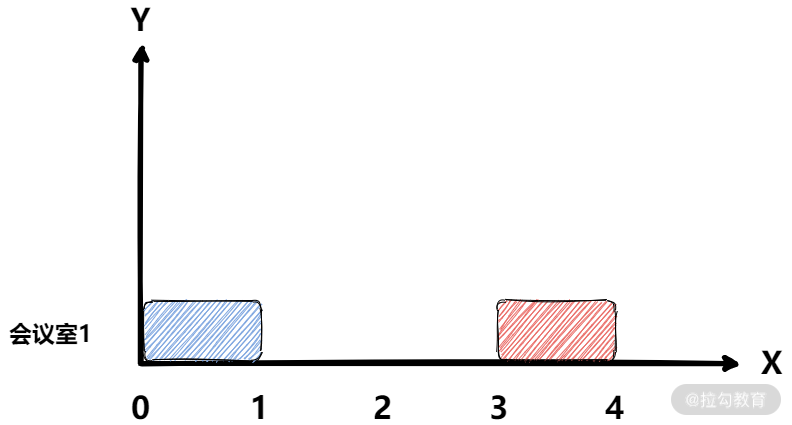
在这种情况下,每个时间点只可以被染上一种颜色,或者没有染上颜色,同样此时最多也只需要一个会议室。
不过,我们还需要处理一种很麻烦的情况,此时 [6, 8] 和 [8, 10] 两个会议的时间点都会将时间点 8 进行染色。那岂不是时间点 8 会有两种颜色?针对这种情况,我们在染色的时候,可以做一点更正。
针对会议时间[start,end]染色时,只需要渲染[start,end),不需要将 end 点进行染色。
此时,即可满足:
区间 [6,8) 与区间[8,10) 不相交。
并且,我们不需要再对这种前后时间相接的情况做特殊判断。
情况 2:需 2 个会议室
前面我们考虑的都是没有重合的情况,接下来,再看一下两个会议室 [0, 2) 和 [1, 4) 有重合的情况。

此时,只需要对 [0, 2) 和区间 [1, 4) 进行染色。我们发现,如果在时刻 1 画一条竖线,会分别遇到两种颜色:蓝色和红色。
情况 3:需多个会议室
前面考虑了需要 1 个和 2 个会议室的情况,接下来我们看一下稍微复杂一点的场景。
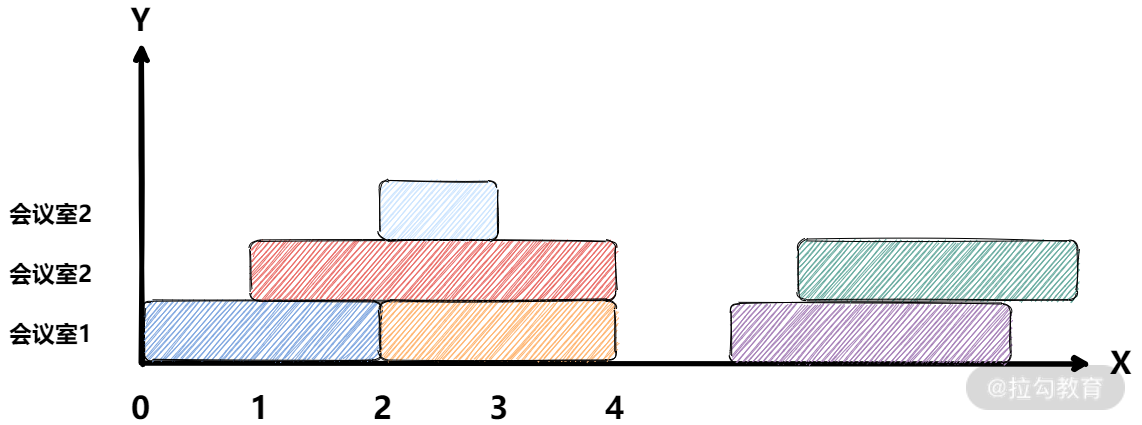
通过画图可以发现规律,y 轴的会议室的数目与某个点染色的次数相关。那么,我们可以把这个题转换为一个更加容易理解的题目:
给定一个数组 A[],再给定一系列区间[start, end),我们将此区间中 A[start…end) 都加上 1。最后求数组 A[] 中的最大值。
差分数组
差分数组是一种求解区间累加的有效手段。我们先考虑只有一个区间 [start, end) 的情况。
一种暴力的写法是下面这样:
for (int i = start; i < end; i++) {A[i]++;}
我们可以通过画图表示操作后的结果,如下图所示:
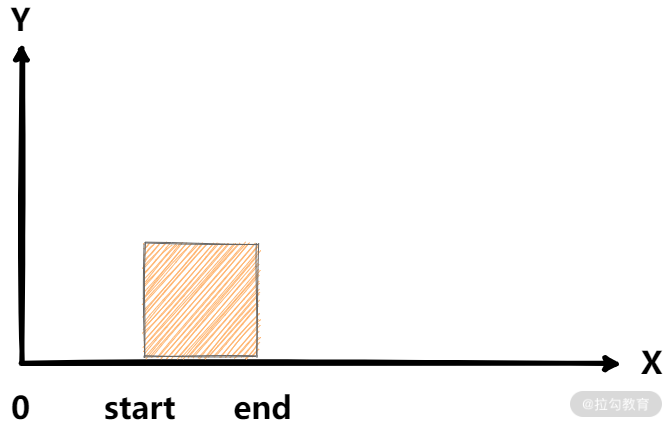
如果我们只关心每个时间点的涨幅与跌幅,那么可以对每个点进行标注,如下图所示:
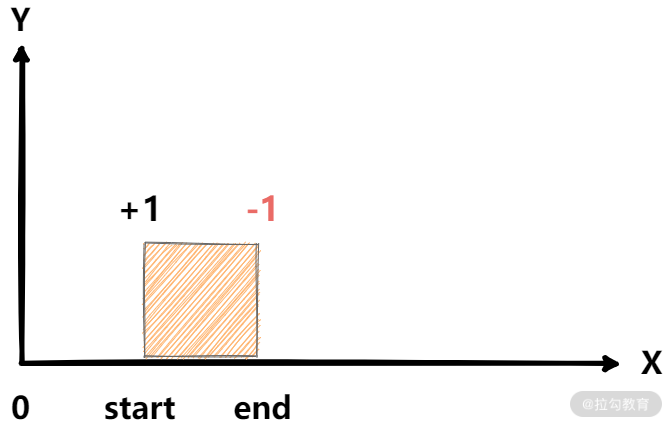
你可以按照如下操作,得到任意时刻的累计值(解析在注释里):
A[start] += 1;A[end] -= 1;pre = 0;for (int i = start; i < end; i++) {pre += A[i];A[i] += pre;}
无论是一个区间还是多个区间,我们都可以参考上述方式进行处理,代码如下(解析在注释里):
for (Interval range: intervals) {A[range.start] += 1;A[range.end] -= 1;}pre = 0;for (int i = start; i < end; i++) {pre += A[i];A[i] += pre;}
基于这个知识点,我还给你留了一个练习题。
练习题 1:假设你有一个长度为n的数组,数组的所有元素初始化为0,并且给定k个更新操作。每个更新操作表示为一个三元组:[startIndex, endIndex, inc]。这个更新操作给子数组A[start``I``ndex````... endIndex](包括 startIndex 和 endIndex)中的每一个元素增加inc。返回执行k个更新操作后的新数组。
改进 1: 哈希表
如果我们直接使用差分数组,好像无法直接破解这个题,因为题目中并没有约定所有整数的范围。比如,如果给定的某个会议时间段是 [0, 10000000000],就无法直接申请 A[10000000000] 这么大的数组。
因此,我们还需要对差分数组做一点改进:可以尝试用哈希表来表示数组。
改进 2:范围
在标准的差分数组中,我们需要返回的是一个操作之后的数组,也就是求出每一个 A[i] 的值。但是在这个题中,只需要拿到数组的最大值就可以了。因此,我们也没有必要求出每一个 A[i] 的值。
综上,可以写出基于差分数组的改进的代码如下(解析在注释里):
class Counter extends HashMap<Integer, Integer> {public int get(Integer k) {return containsKey(k) ? super.get(k) : 0;}public void add(Integer k, int v) {put(k, get(k) + v);}}public class Solution {* @param intervals: an array of meeting time intervals* @return: the minimum number of conference rooms required*/public int minMeetingRooms(List<Interval> intervals) {Counter A = new Counter();for (Interval range: intervals) {final int start = range.start;final int end = range.end;A.add(start, 1);A.add(end, -1);}List<Integer> idx = new ArrayList<>(A.keySet());Collections.sort(idx);int pre = 0;int ans = 0;for (Integer i: idx) {pre += A.get(i);ans = Math.max(ans, pre);}return ans;}}
复杂度分析:时间复杂度为 O(NlgN),空间复杂度为 O(N)。
我们发现,这个题目的考点就是在差分数组上的两点变化:
- 利用哈希表表示数组;
- 由于只需要求最大值,因此我们求出区间端点的值就可以了。
接下来,我们来看另外一种思路。
特点 2:变招 1
我们继续讨论一下差分数组的解法。在本题中,我们需要的并不是一个标准的差分解法。经过分析之后,实际上只需要处理以下情况:
- 给定区间 [start, end);
- 只需要遇到 start 时 +1;
- 只需要遇到 end 时 -1;
- 然后再利用累计求和的方式计算每个位置的值。
在前面我们用了哈希数组的办法,那么,哈希数组就是必需的吗?
由于我们并不像差分数组一样返回操作之后的整个数组,而是返回最大值。因此只需要经过以下两步,就可以得到最大值。
- Step 1. 将所有的下标放到一个数组中,并且进行排序。
- Step 2. 从头倒尾遍历下标,如果遇到区间的起始点,那么 +1;如果遇到区间的终点,那么 -1。
操作伪代码如下:
item = [收集了所有的下标]sort(item)ans = 0pre = 0for 坐标 in item:if 坐标是区间的起始点:pre += 1else:pre -= 1ans = max(ans, pre)return ans
这里还有两个地方需要处理:
1 ) 如何判断经过排序之后的下标,是区间的终点还是一个区间的起始点?
解决方法:在放到 item 里面的时候,我们可以将起始点设置为正值,终点设置为负值。
2 )如果经过排序之后的下标分了正负,那么一个区间的终点将会位于 x 轴的负半轴,起始点位于 x 轴的正半轴,这并没有按照原本的坐标排序。
解决方法:排序时,我们只需要按照下标的绝对值排序即可。
基于这样的处理技巧,可以写出代码如下:
public class Solution {* @param intervals: an array of meeting time intervals* @return: the minimum number of conference rooms required*/public int minMeetingRooms(List<Interval> intervals) {List<Integer> item = new ArrayList<>();for (Interval range: intervals) {item.add(range.start);item.add(0 - range.end);}Collections.sort(item, new Comparator<Integer>() {public int compare(Integer a, Integer b) {return Math.abs(a) - Math.abs(b);}});int ans = 0;int pre = 0;for (int i = 0; i < item.size(); i++) {if (item.get(i) >= 0) {pre++;} else {pre--;}ans = Math.max(ans, pre);}return ans;}}
复杂度分析:时间复杂度为 O(NlgN),空间复杂度为 O(N)。
在这里,我们已经快找不到差分数组的影子了,但是本质上还是基于差分数组进行求解。那么,还有其他的解法吗?
特点 3:变招 2
前面在处理区间的时候:是将所有区间的起始点标记为非负,区间的终点标记为负数;排序时按照绝对值进行排序。然后再利用差分数组的核心思想:遇到区间的起始点 +1;遇到区间的终点 -1。
那么还有没有其他的招法呢?我们再认真地研究一下这个题目,不难发现,破题的关键就在两处条件:
- 需要将所有的坐标排序,并且需要知道每个坐标是属于一个区间的起始点还是终点。即顺序遍历坐标,知道每个坐标是起始点还是终点;
- 利用差分数组的核心思想,然后求出最大值。
根据条件 2,我们已知可以利用差分数组的思路,那么条件 1 这里还可以用别的方法吗?下面我们尝试完成条件 1 。
首先将所有区间的起始点坐标放到 starts 数组中,将所有区间的终点坐标放到 end 数组中。然后,再将 starts 和 end 采用合并排序的方法进行合并(注意,此时我们不是直接使用合并排序,准确来说是使用合并排序中的合并的技巧)。
此时,我们可以达成条件 1 的两个目的:
- 顺序遍历每个坐标;
- 知道每个坐标是区间起始坐标,还是终点坐标。
伪代码如下:
starts = [...区间的起始点...]ends = [...区间的终点...]sort(start);sort(ends);slen = len(starts)elen = len(ends)i = 0j = 0while i < slen || j < elen:if j >= elen || i < slen:遍历到了start[i];并且我们知道这个坐标是区间的起始点else:遍历到了end[i];并且我们知道这个坐标是区间的终点
基于这样的思想,再加上我们的差分核心思路,那么就可以写出如下代码了(解析在注释里):
public class Solution {* @param intervals: an array of meeting time intervals* @return: the minimum number of conference rooms required*/public int minMeetingRooms(List<Interval> intervals) {final int N = intervals == null ? 0 : intervals.size();int[] start = new int[N];int[] end = new int[N];int i = 0;for (Interval range: intervals) {start[i] = range.start;end[i] = range.end;i++;}Arrays.sort(start);Arrays.sort(end);i = 0;int j = 0;int pre = 0;int ans = 0;while (i < N || j < N) {if (j >= N || i < N && start[i] < end[j]) {pre++;i++;} else {pre--;j++;}ans = Math.max(ans, pre);}return ans;}}
复杂度分析:时间复杂度为 O(NlgN),空间复杂度为 O(N)。
接下来,我们再看看有没有其他的解法。
特点 4:最少
再回到原始题目,要想会议室最少,那么我们在拿到一个 meeting = [start,end] 的时候,尽量不去开新的会议室,而是选择一个已有会议结束时间<= start 的会议室开会。
要做到这一点,我们需要记录每个会议室的结束时间;当给定 meeting = [start,end] 的时候,就需要找到一个 <= start 的会议室提供给这个 meeting 使用。
到这里,不知道你是否想起了我们在《03 | 优先级队列:堆与优先级队列,筛选最优元素》中介绍的 “例 3”。我们可以把会议室也放到优先级队列中,每次总是取出结束时间最早的会议室。
由于给定的所有的 meeting 并没有排好序。因此,我们还需要做一点预处理——对 meeting 进行排序。此时你还会面临一个问题,在排序的时候,meeting 有 [start,end],那么应该按照 start 值来排序,还是按照 end 来排序呢?
答案是按照 start 值来排序。因为我们在选择会议室的时候,需要两个输入,分别是 meeting 的开始时间 start 和会议室的结束时间。
基于这样的思想,我们就可以写出如下的代码(解析在注释里):
public class Solution {public int minMeetingRooms(List<Interval> intervals) {final int N = intervals == null ? 0 : intervals.size();Collections.sort(intervals, new Comparator<Interval>() {public int compare(Interval a, Interval b) {return a.start - b.start;}});Queue<Integer> meetingRooms =new PriorityQueue<>((v1, v2) -> v1 - v2);for (Interval meeting : intervals) {if (!meetingRooms.isEmpty() &&meetingRooms.peek() <= meeting.start) {meetingRooms.poll();meetingRooms.add(meeting.end);} else {meetingRooms.add(meeting.end);}}return meetingRooms.size();}}
复杂度分析:时间复杂度为 O(NlgN),空间复杂度为 O(N)。
总结
最后,我将本讲用到的知识整理成在一张思维导图中,方便你复习。
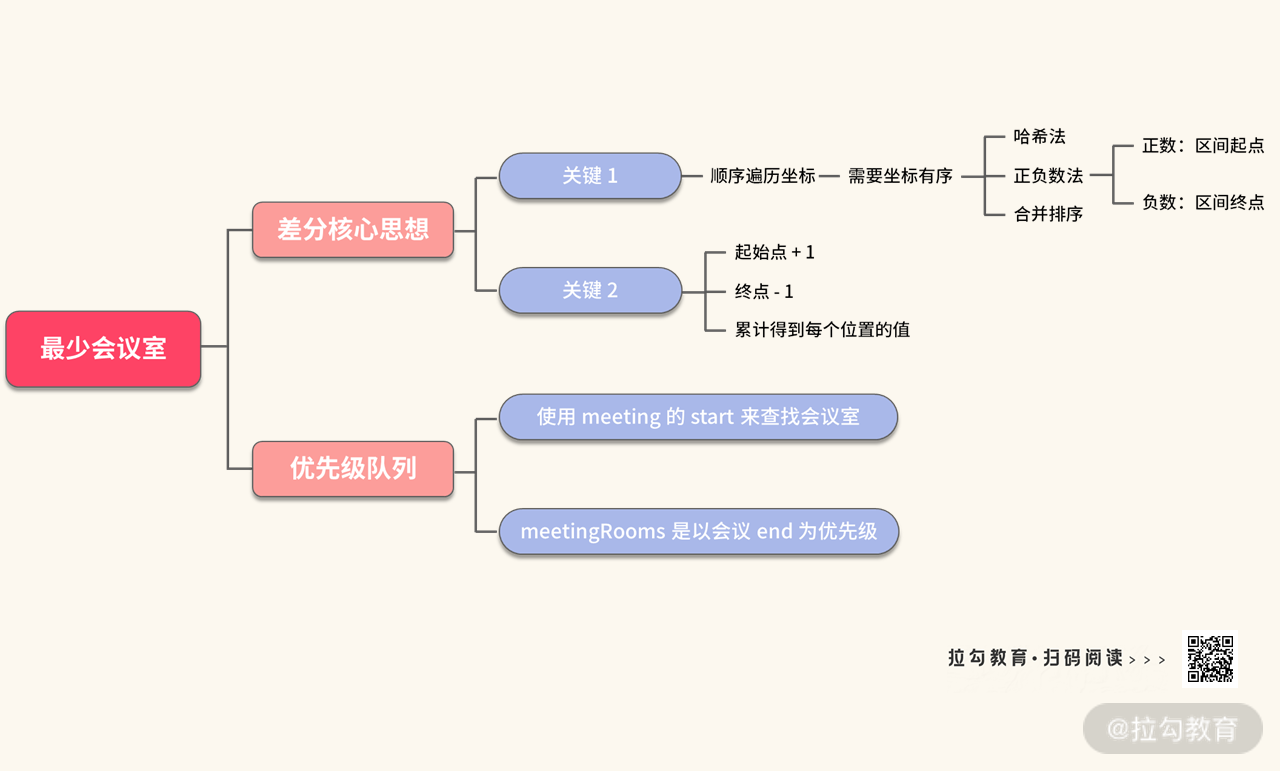
通过总结我们发现,这个题目的核心解法实际上只有两种,但是基于差分方法又出现了三种 “伪多解” 的做法,我们一一进行了分析,透过代码,相信你也学会了如何运用多种技巧来满足题目的条件。
当然,在面试中,如果你遇到这道题之后,面试官有可能还会深入地问你一些问题,比如下面这道一个思考题。
题目仍然不变,要求输出最少会议室的个数,并且还要输出每个会议室里面召开哪些会议。
输入:会议时间表[[0,30],[5,10],[15,20]]
输出:最少需要的会议室数量 2,[[0,30]] 放到会议室 1,[[5,10], [15,20]] 放到会议室 2。
你可以自己尝试求解这道题目,把答案写在留言区,我们一起讨论。关于这道会议室的题目就介绍到这里。接下来,下一讲介绍 “22 | 数据结构模板:如何让解题变成搭积木?”,让我们继续前进。

