15 | 字符串查找：为什么我最终选择了 BM 算法？

数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育

这一模块我会带你挖掘题目的特点，再对标不同的数据结构与算法，从而得出不同的解法。虽然我们只介绍一道题，但是解题的方法却有很多种，我会带你尝试从不同的角度去击破一道题。

关于字符串查找，可以说是一类非常经典的面试题，它可以考察候选人多方面的技能，比如代码基本功、深度思考能力，以及知识广度等。

• 代码基本功：需要注意各种空字符串，数组访问越界等边界的处理。
• 深度思考能力：各种字符串查找的算法代码本身不会太长，但是需要你深入理解其原理才能正确地写代码，并且清晰地讲述思路。
• 知识广度：字符串查找涉及很多种算法，可以借此了解候选人的知识积累。

在本讲，将以一道字符串查找的面试题为引，带你深入探索 “一题多解” 的思考方式，有利于你掌握快速审题和解题的能力。具体来说，学完本讲你将收获：

• 暴力搜索算法与本质
• KMP 算法的改进与扩展
• BM 算法
• Sunday 算法

字符串查找

【题目】实现 strStr() 函数。给定一个 main 字符串和一个 sub 字符串，在 main 字符串中找出 sub 字符串出现的第一个位置 （从 0 开始）。如果不存在，则返回 -1。

示例 1

输入: main = “hello”, sub = “ll”

输出: 2

注意：有的文章也把 sub 字符串称为 pattern 字符串（模式串）。

暴力查找算法

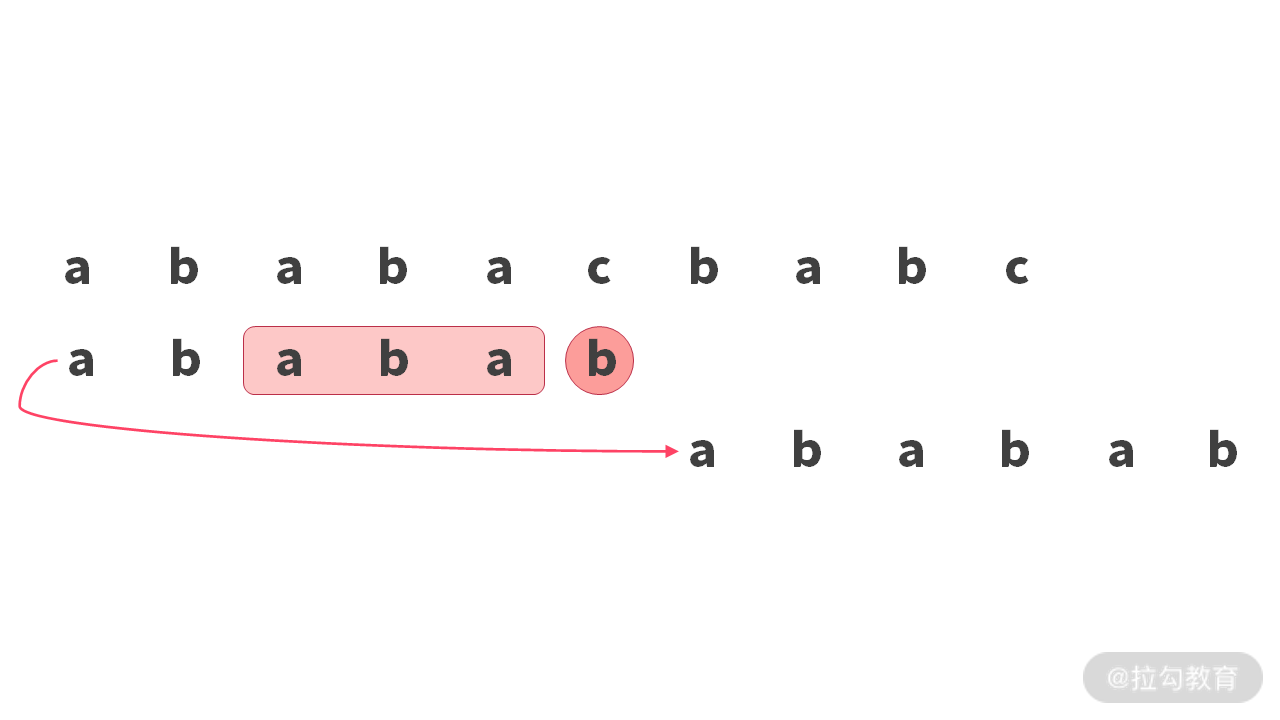
如果你在面试的时候，拿到这道题没有任何思路，可以先选择一个暴力求解的方法。具体思路就是把每一个 main 字符串都当成一个潜在的起始位置，然后依次向后匹配。

这里我们用一个例子说明一下暴力查找算法的思路。注意，图中较长的字符串为主串 main，较短的字符串为子串 sub。

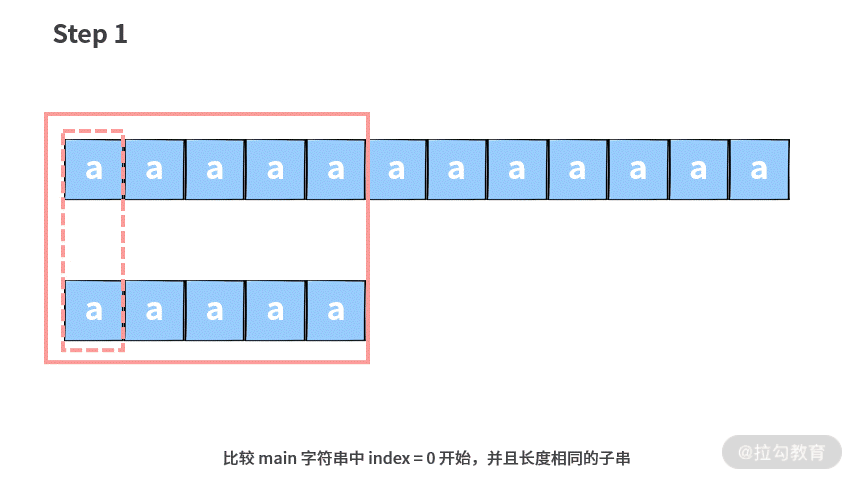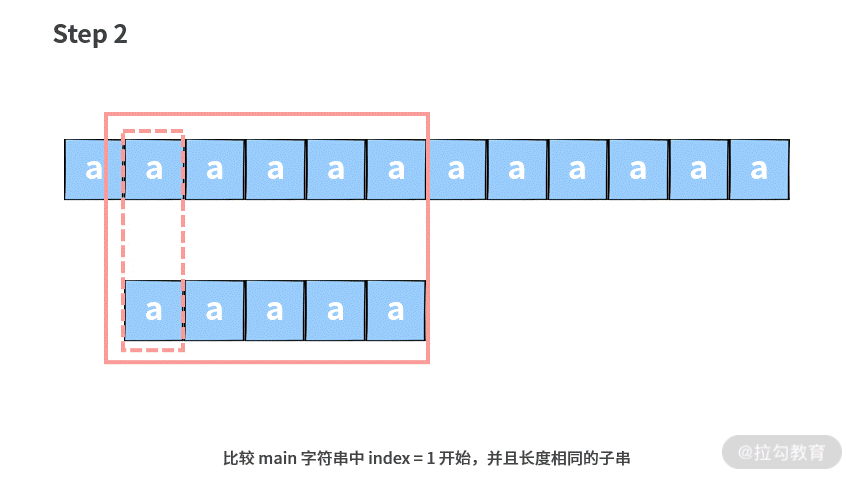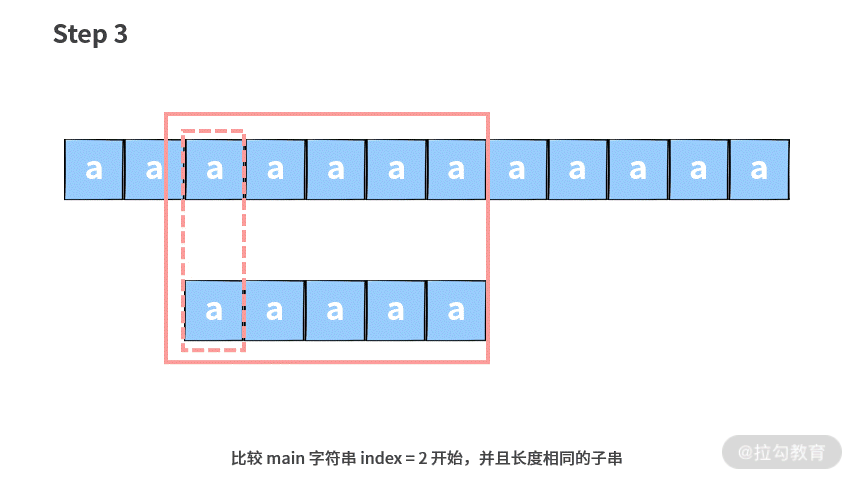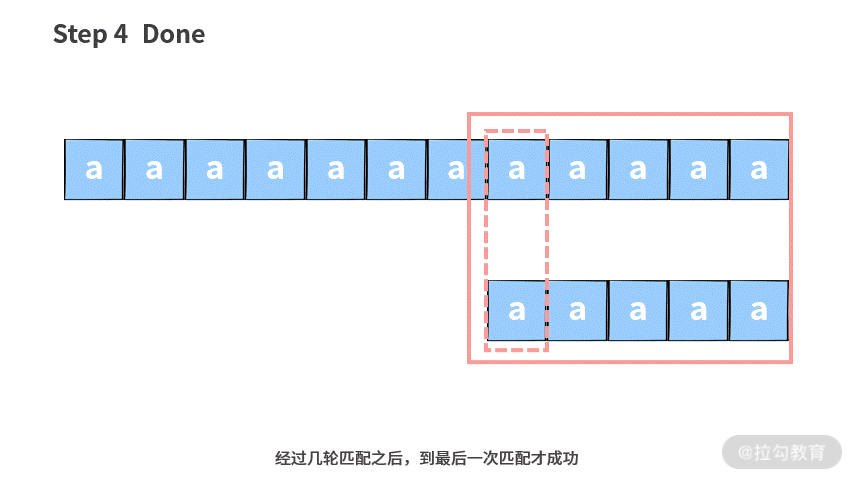
基于这样的思路，我们可以写出代码如下（解析在注释里）：

class Solution {
public int strStr(String main, String sub) {
if (sub == null || sub.length() == 0) {
return 0;
        }
if (main == null || main.length() == 0) {
return -1;
        }
for (int i = 0; i < main.length(); i++) {
boolean hasFind = true;
for  (int j = 0; j < sub.length(); j++) {
if (i + j >= main.length() ||
                    main.charAt(i+j) != sub.charAt(j)) {
                    hasFind = false;
break;
                }
            }
if (hasFind) {
return i;
            }
        }
return -1;
    }
}

代码：Java/C++/Python

复杂度分析：最坏情况下时间复杂度为 O(N×M)，其中 N 为 main 字符串的长度，M 为 sub 字符串的长度。空间复杂度为 O(1)。

【分析】首先我们分析一下这种方法的缺点：时间复杂度高，如果字符较长，不能快速定位。

那么这种算法有没有优点呢？实际上还是有的：

• 实现简单；
• 不需要额外空间，在字符串较短的情况下，算法的运行速度很快；
• 大部分时候，我们处理的都是较短的字符串。

虽然其他一些算法是线性时间复杂度，但是由于需要开辟额外的内存空间，在一定情况下：

• 涉及内存申请与释放，内存的申请与释放都会带来较大的时间开销；
• 可能触发带内存 GC 语言的内存垃圾回收，导致程序运行速度变得更慢。

为了避免申请内存，Java 语言内置的 IndexOf 方法的实现就是采用的这种思路。我们在面试的时候，除了要把代码写对，还需要亮出更多手中的 “法宝”，向面试官展示出自己的优势。比如：

• 指出这种算法实现的优点和缺点；
• 什么情况下用这种算法？什么情况下不应该用？

在面试中，如果你仅是把暴力的方法写对，很有可能还是不能通过面试。因为：

字符串查找题目，用暴力方法写对的人~~ 实在太多了 = =。

KMP 算法

接下来我们讨论 KMP 算法。如果你以前在学习 KMP 算法的过程中，觉得很难，或者说压根看不懂。相信我，这不是你的错。因为学习 KMP 算法需要一些前置知识，在这里，我们就将这些前置知识讲透。

只要你跟着我的思路，一步一步思考，学完本讲肯定能看懂 KMP 。

前缀与前缀集

首先我们要学习的第一个概念是前缀，一个长度为 N 的字符串 S 的前缀需要满足如下条件：

• 非空
• 不是 S 自身
• 是包含 S[0] 的连续子串

比如，给定一个字符串 S = “ABC”，那么所有的前缀有：

我们把所有前缀放到一个集合中，就构成了字符串的前缀集。

后缀与后缀集

第二个概念是后缀，一个长度为 N 的字符串 S 的后缀需要满足如下条件：

• 非空
• 不是 S 自身
• 是包含最后一个字符 S[N-1] 的连续子串

比如，给定一个字符串 S = “ABC”，那么所有的后缀有：

我们把所有后缀放到一个集合中，就构成了字符串的后缀集。

前后缀的最长匹配

给定一个字符串，我们想知道它的前缀集和后缀集里面最长且相同的字符串是什么，比如：

S = "ababa";
前缀集 = {
"a",
"ab",
"aba",
"abab",
}
后缀集 = {
"a",
"ba",
"aba",
"baba",
}

那么两个集合的交集就是：

我们还需要在这个交集里面找到最长的字符串，就是 “aba”，这里我们称为前后缀的最长匹配。

PMT 表（Partial Match Table）

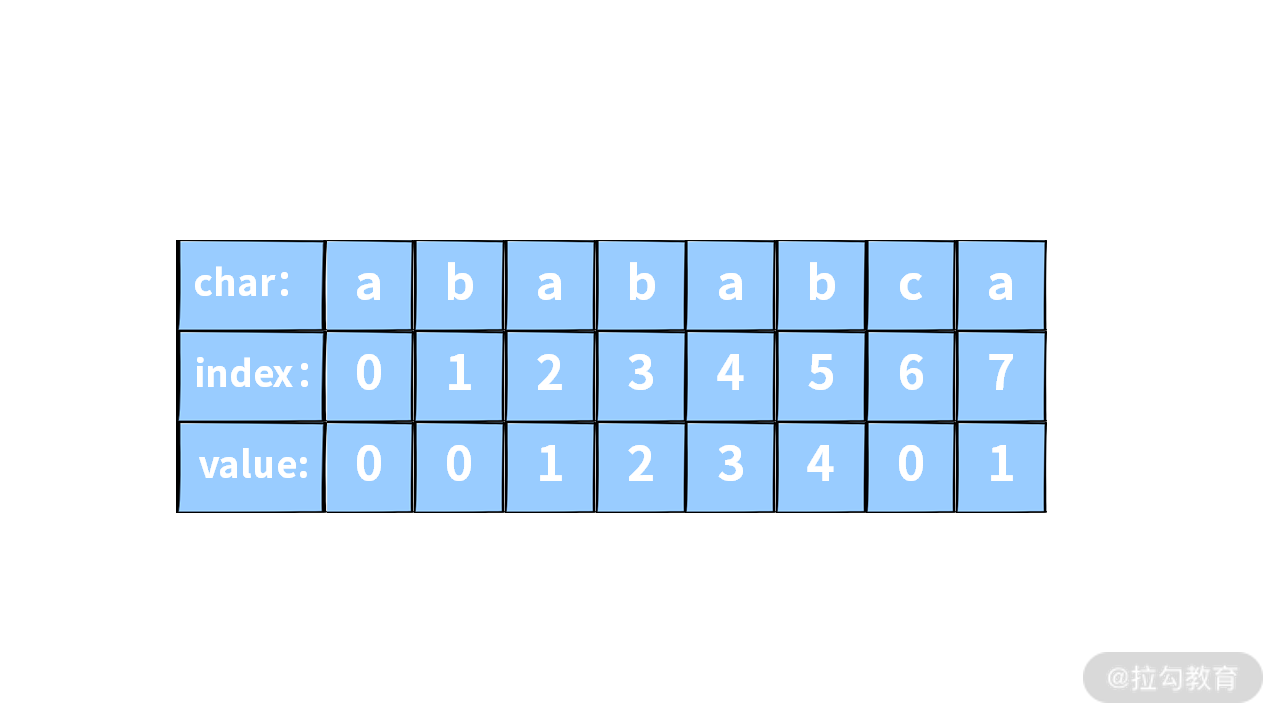
PMT 表（本质上就是一个数组）中的每一项 PMT[i]，表示的是一个字符串 S[0..i] 的前后缀的最长匹配的长度。这里我可以用如下操作表示 PMT 表的含义：

S = "abababca"; 
PMT[0] = 前后缀的最长匹配(S[0]= "a") = "" = 0
PMT[1] = 前后缀的最长匹配(S[0..1]= "ab") = "" = 0
PMT[2] = 前后缀的最长匹配(S[0..2]= "aba") = "a" = 1
PMT[3] = 前后缀的最长匹配(S[0..3]= "abab") = "ab" = 2
PMT[4] = 前后缀的最长匹配(S[0..4] = "ababa") = "aba" = 3
PMT[5] = 前后缀的最长匹配(S[0..5] = "ababab") = "abab" = 4
PMT[6] = 前后缀的最长匹配(S[0..6] = "abababc") = "" = 0
PMT[6] = 前后缀的最长匹配(S[0..6] = "abababca") = "a" = 1

注意：PMT[i] 求的就是字符串 S[0..i]的前后缀的最长匹配。所以，字符串 S = “abababca” 的 PMT 表如下：

PMT 的用途

现在你已经知道了 PMT 表的定义，以及如何计算 PMT 表。但直接根据定义来计算，复杂度有点高。不过没关系，我们后面马上就会介绍如何高效地计算 PMT 表。

在这之前，我先介绍一下 PMT 表的用途。重要的话说三遍：

PMT 表的用途是解开 KMP 算法的关键！

PMT 表的用途是解开 KMP 算法的关键！

PMT 表的用途是解开 KMP 算法的关键！

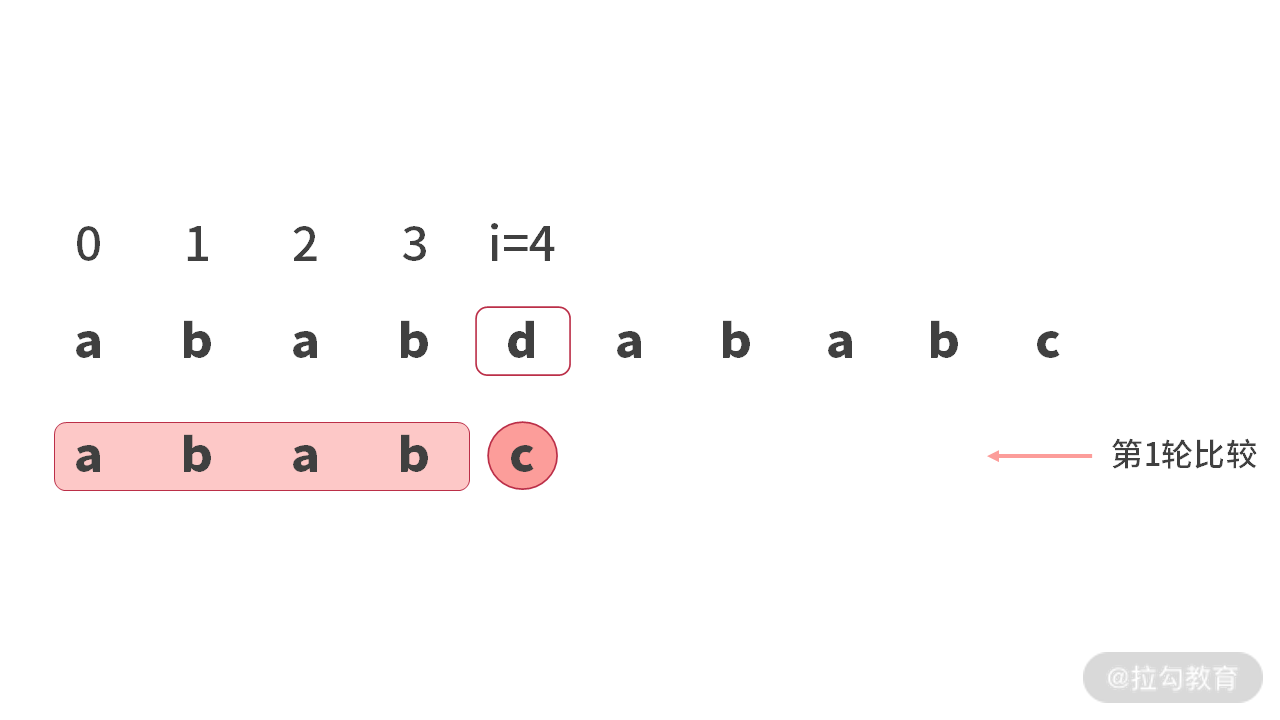
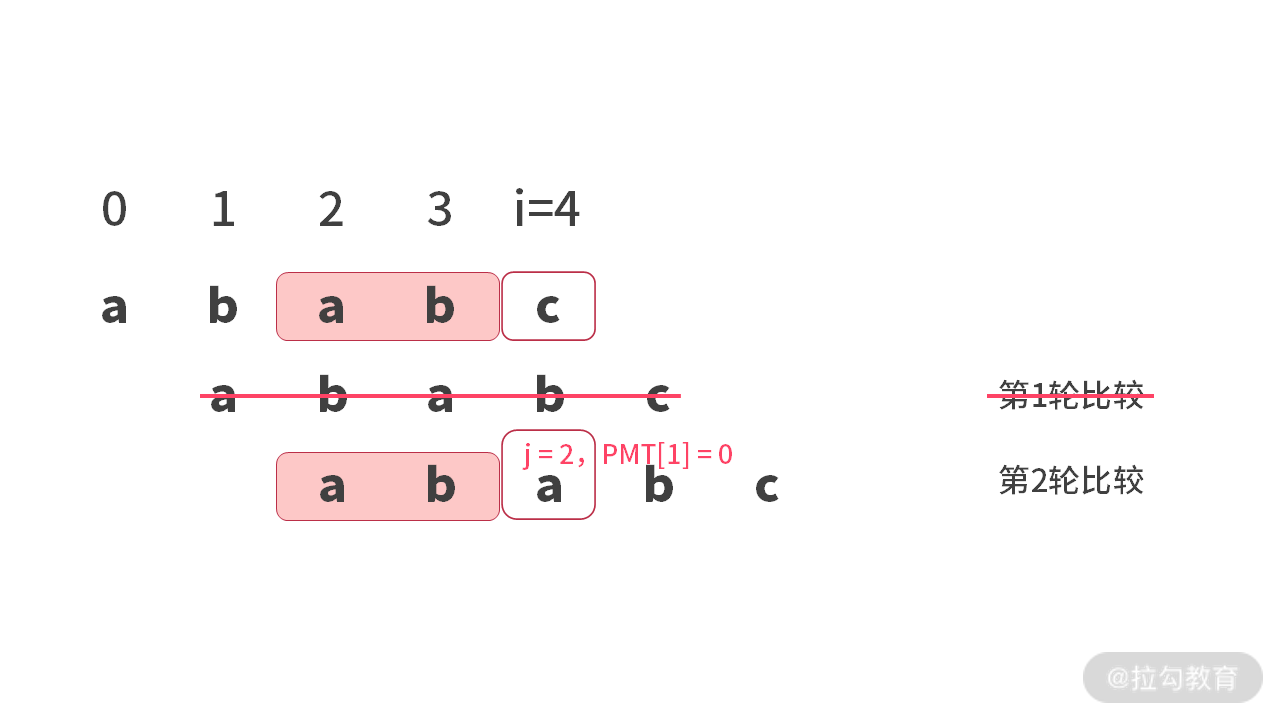
那么，PMT 表到底能用来做什么呢？我们再来看一下暴力算法中可以优化的地方。比如，要在字符串 main = “ababdababc” 中找到 sub=”ababc”。

第 1 轮比较时，会在 main[4] 处比较 (‘d’ != ‘c’) 失败。如下图所示：

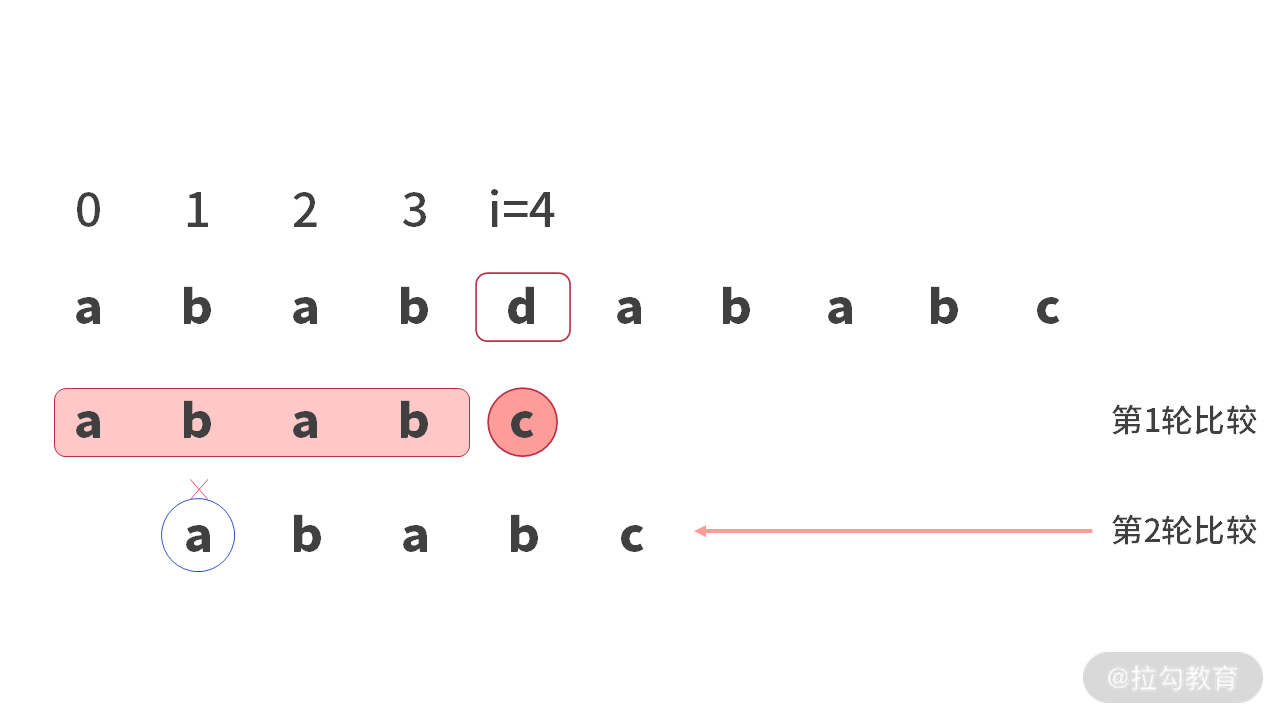
进行第 2 轮比较时，会在 main[1] 处比较 (‘b’ != ‘a’) 失败。如下图所示：

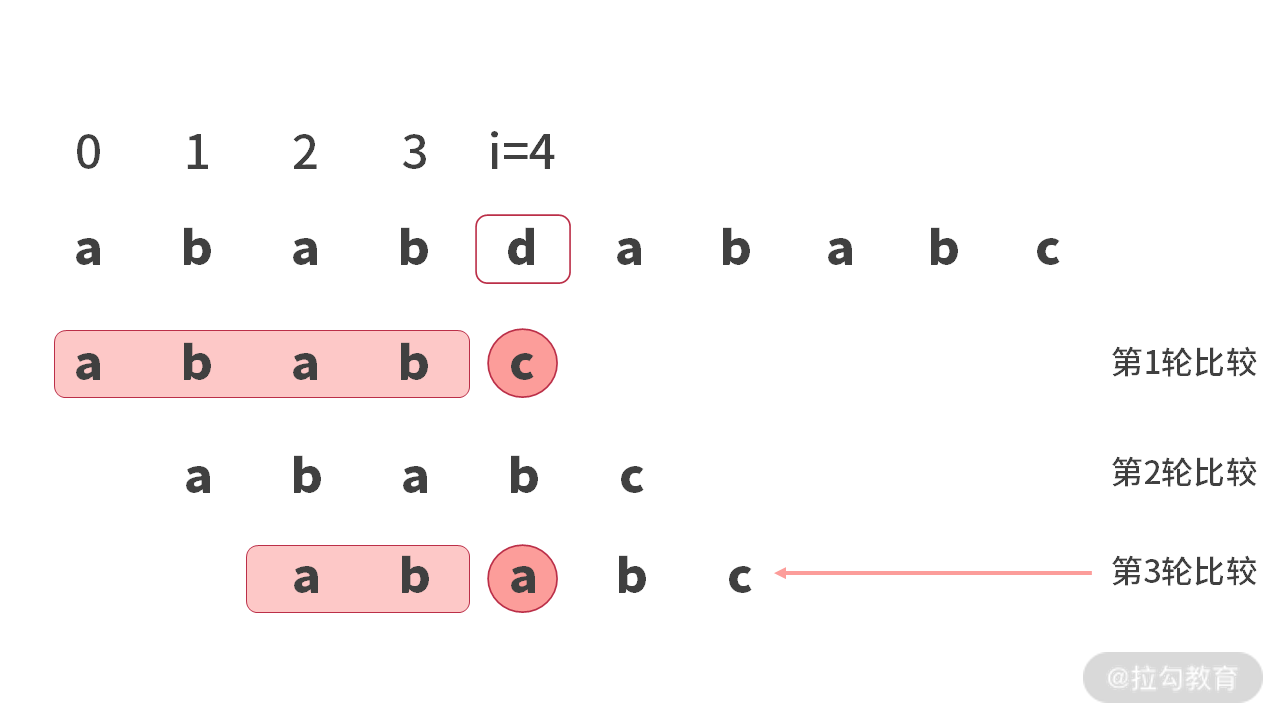
进行第 3 轮比较时，会在 main[4] 处比较 (‘d’ != ‘a’) 失败。如下图所示：

接下来，进行第 4 轮比较时，会在 main[3] 处比较 (‘b’ != ‘a’) 失败。如下图所示：

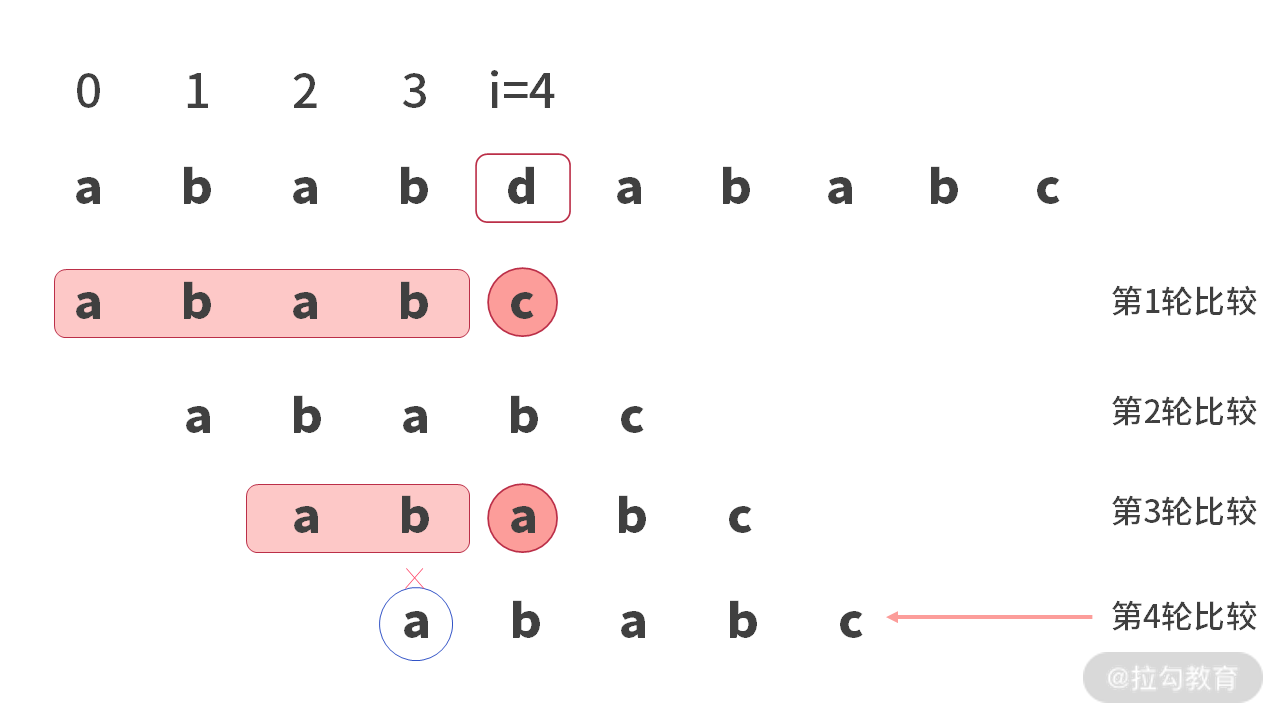
进行第 5 轮比较时，会在 main[4] 处比较 (‘d’ != ‘a’) 失败。凡是比较失败下标小于 4 的情况，都是无效比较（比如第 2 轮，第 4 轮）。因为这种比较还没有跑到 main[4] 就挂了（第 2 轮挂在 main[1]，第 4 轮挂在 main[3]）。

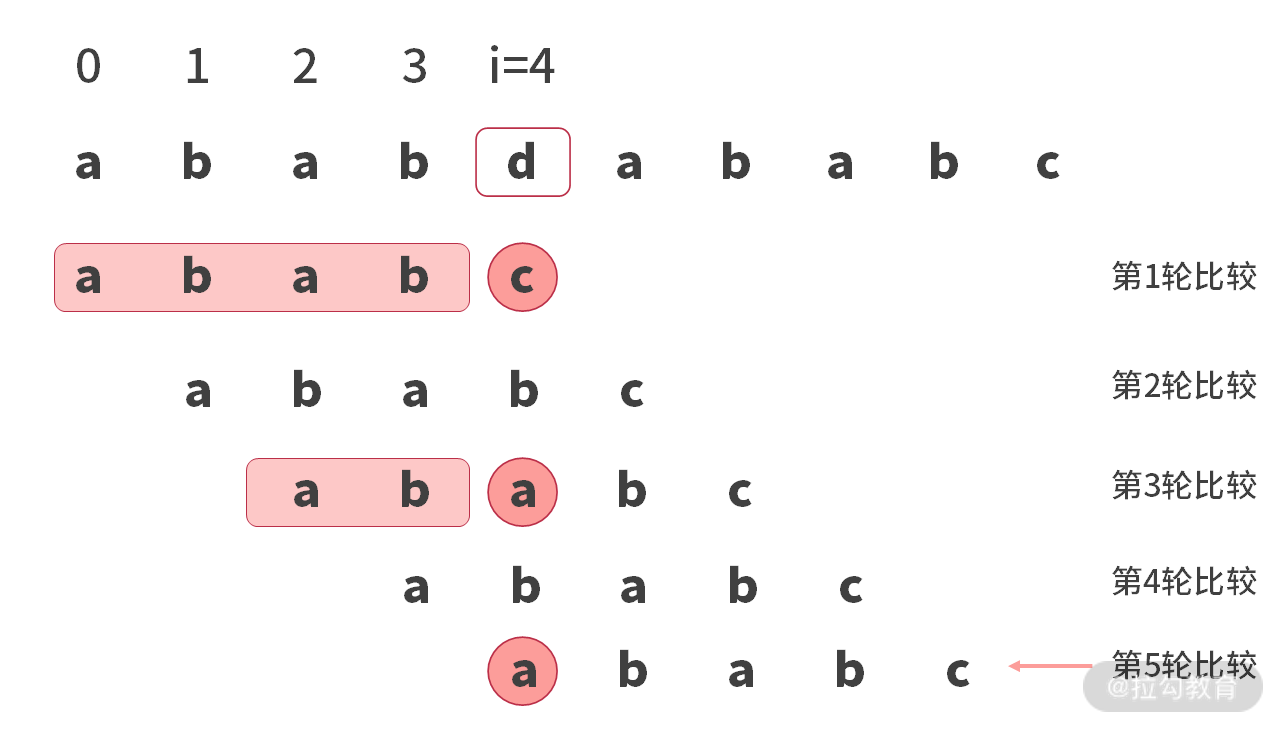
如果我们只看有效比较（第 1 轮、第 3 轮、第 5 轮），然后分别观察字符串已经匹配的部分，如下所示：

第1轮匹配成功的部分是: "abab"
第3轮匹配成功的部分是："ab"
第5轮匹配成功的部分是: ""

联系前面讲到的前后缀的最长匹配知识，可以发现：

"abab"的前后缀最长匹配为"ab"
"ab"的前后缀最长匹配为""

因此，我们可以总结出一个规律：当某个匹配位置失败，进行下一次比较时，取已经匹配成功部分的 “前后缀的最长匹配” 即可。这样，比较时就能够从第 1 轮，直接跳到第 3 轮，然后再从第 3 轮直接跳到第 5 轮。如下图所示：

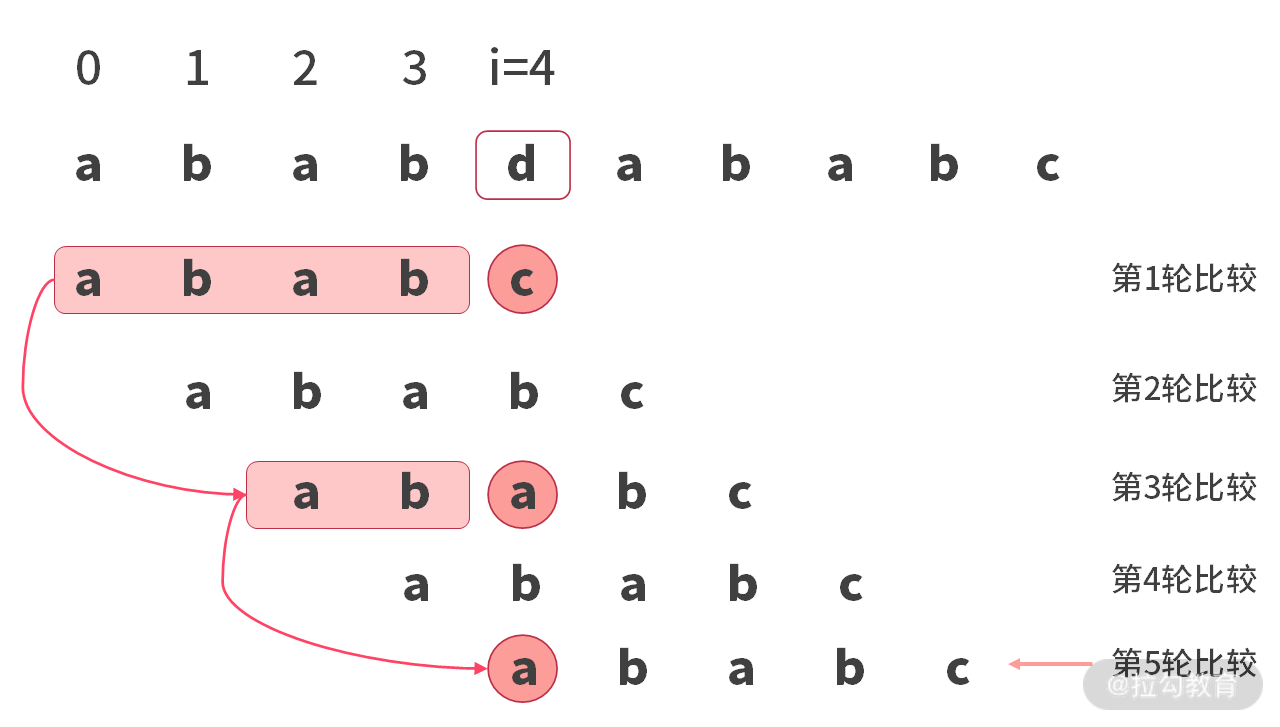
到这里，就可以发现 PMT 表的作用了。我们先给出 sub=”ababc” 字符串的 PMT 表，如下所示：

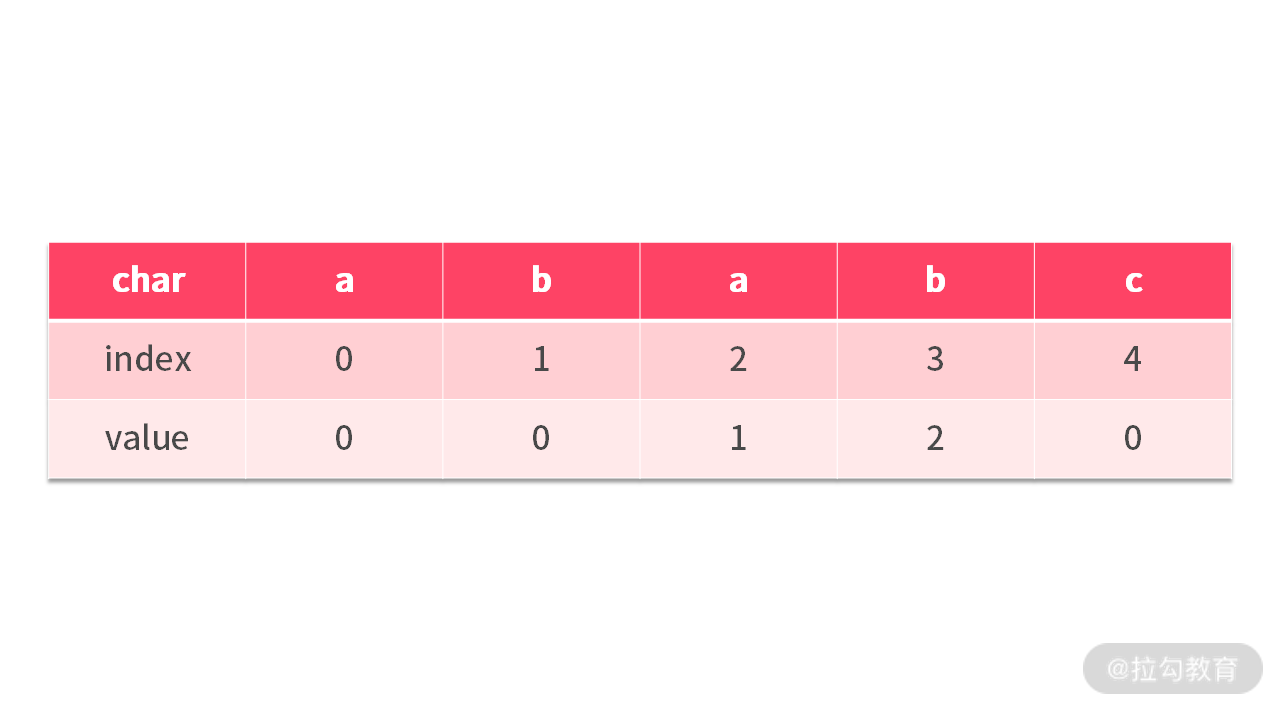
"abab"的前后缀最长匹配 = "ab" = PMT[3] = 2
"ab"的前后缀最长匹配 = "" = PMT[1] = 0

结合 PMT 表，还可以发现，当在 sub[j] 位置比较失败，下一个可能成功的比较位置就是 PMT[j-1]。

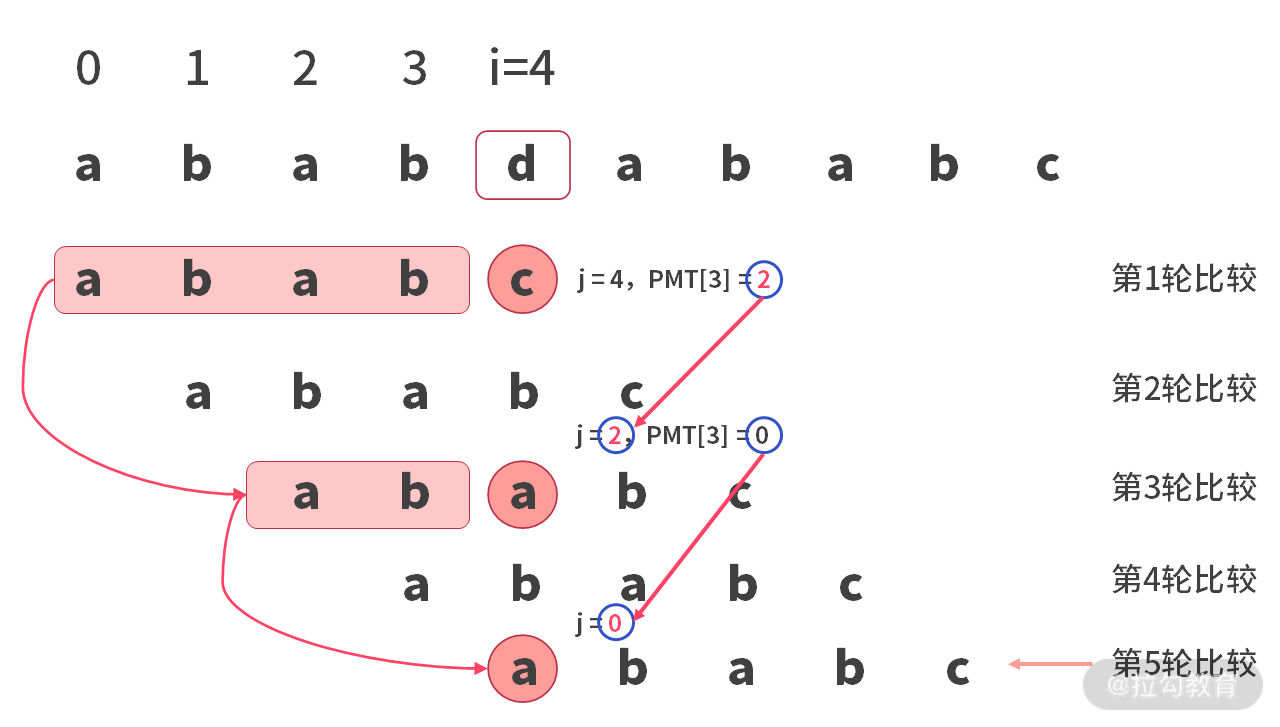
因此，经过前面的分析，我们总算弄明白了 PMT 表的作用。就是：

比较失败的时候，可以利用 PMT 表迅速地转到下一个有可能成功的比较上。
直接跳过一些无效比较。

当我们有 PMT 表的时候，就可以跳过无效比较的代码写出如下代码：

i = 0
j = 0
while i < main.length() and j < sub.length():
if main[i] == sub[j]:
    i++
    j++
else:
    j = pmt[j-1]

但是这样写，会在 j = pmt[j-1] 这里出错，原因在于 j 是可以取 0 的。并且，当 j = 0 的时候，如果比较失败，应该移动 i。

所以正确的代码应该写成如下（是的，还不用关心 pmt 数组怎么算的）：

int strStr(String main, String sub) {
int i = 0;
int j = 0;
final int alen = main.length();
final int blen = sub.length();
int[] PMT = buildPMT(sub);
while (i < alen && j < blen) {
if (main.charAt(i) == sub.charAt(j)) {
        i++;
        j++;
      } else {
if (j == 0) {
          i++;
        } else {
          j = PMT[j-1];
        }
      }
    }
return j == blen ? i - blen : -1;
}

代码：Java/C++/Python

复杂度分析：时间复杂度为 O(N + M)，其中 N 表示 main 字符串的长度，而 M 表示 sub 字符串的长度。空间复杂度为 O(M)。

next 数组怎么来的？

你可能会问：我们学的 KMP 算法里面都是有 next 数组，为什么你这里只有 PMT 数组？

其实关键在于这里面有一个优化。因为每次访问 pmt[] 数组的时候，都是用 pmt[j-1]。每次访问的时候，都还需要 j-1，因此多了一个减法。那么有没有办法把这个减法给节省掉？

为了节省运算量，我们在 pmt[] 数组的前面插一个数 -1。

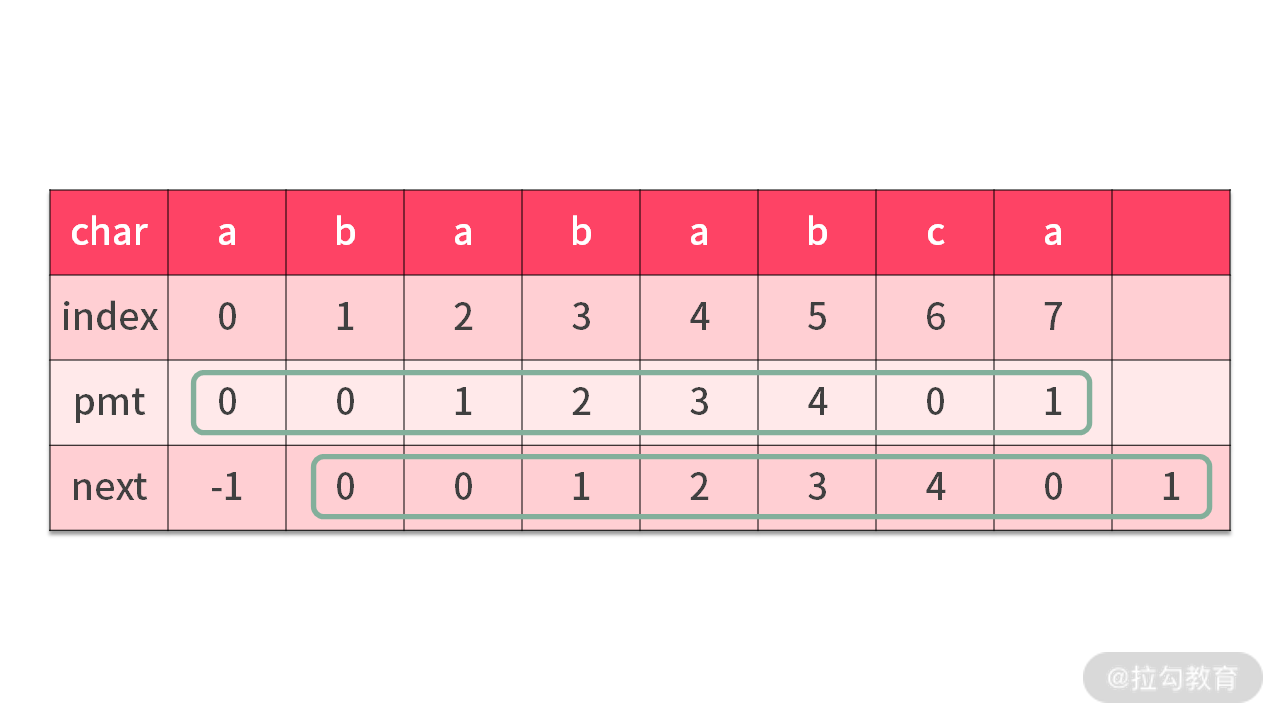
那么就形成了 next 数组。既然有了这样一个数组，比较的代码就可以更改 2 个匹配失败的地方，如下图所示：

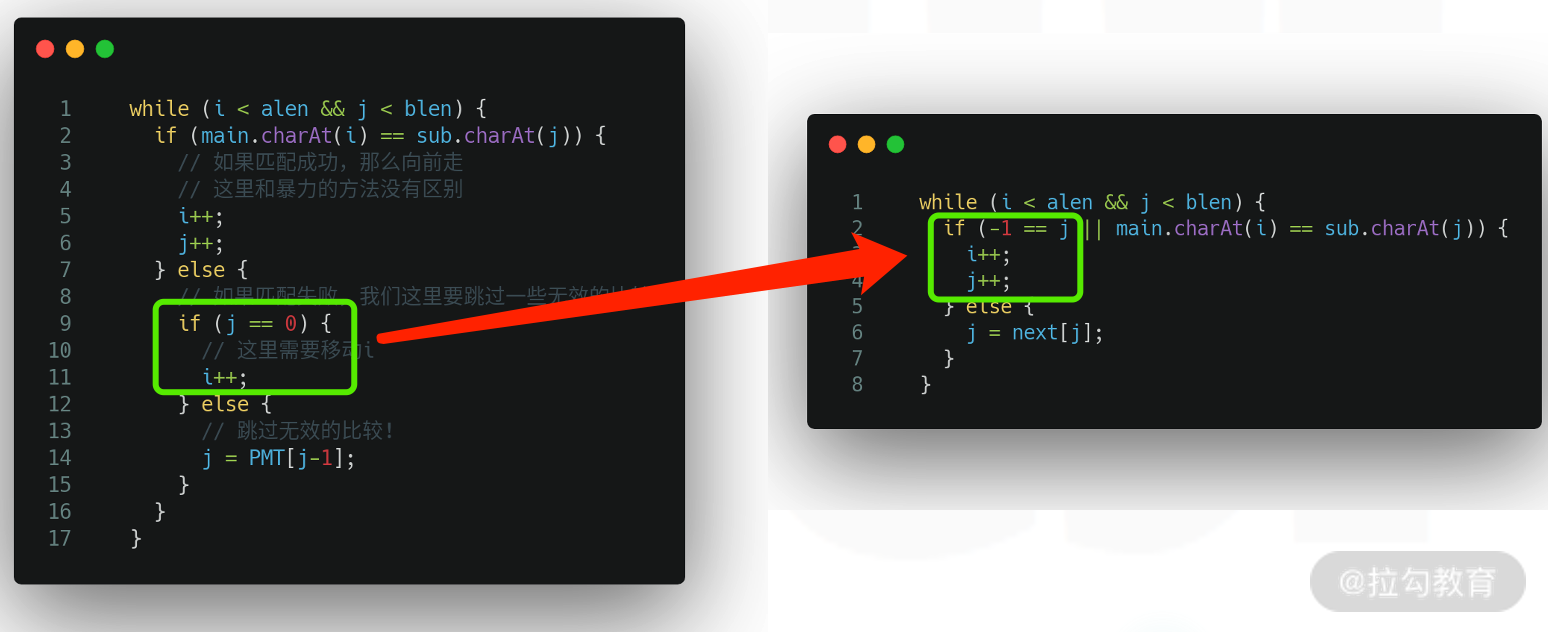
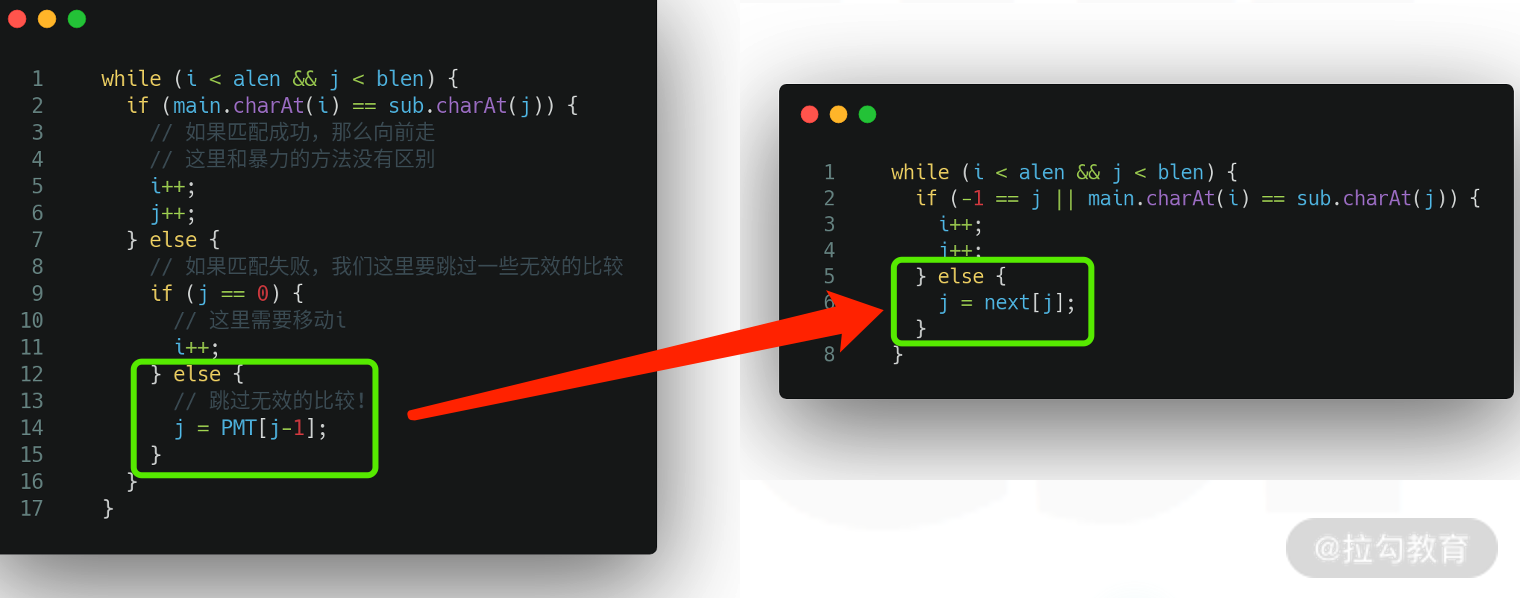
更改之后的代码就变成如下的样子（解析在注释里）：

int strStr(String main, String sub) {
int i = 0;
int j = 0;
final int alen = main.length();
final int blen = sub.length();
int[] next = buildNext(sub); 
while (i < alen && j < blen) {
if (-1 == j || main.charAt(i) == sub.charAt(j)) {
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
return j == blen ? i - blen : -1;
}

next 数组的计算

讲完主程序之后，接下来我们应该看一下如何计算 sub 字符串的 next 数组。首先应该考虑整个字符串的最后一步，也就是找整个字符串的前后缀的最长匹配。

我们分 4 个阶段进行讲解：

• 暴力方法
• 跳过无效比较方法 1
• 跳过无效比较方法 2
• 写代码

第一个阶段：暴力方法

暴力方法的思路是：不停地移动字符串的前缀，从最长的可能开始暴力比较。那么当字符串为 sub = “ababc” 的时候，匹配过程如下：

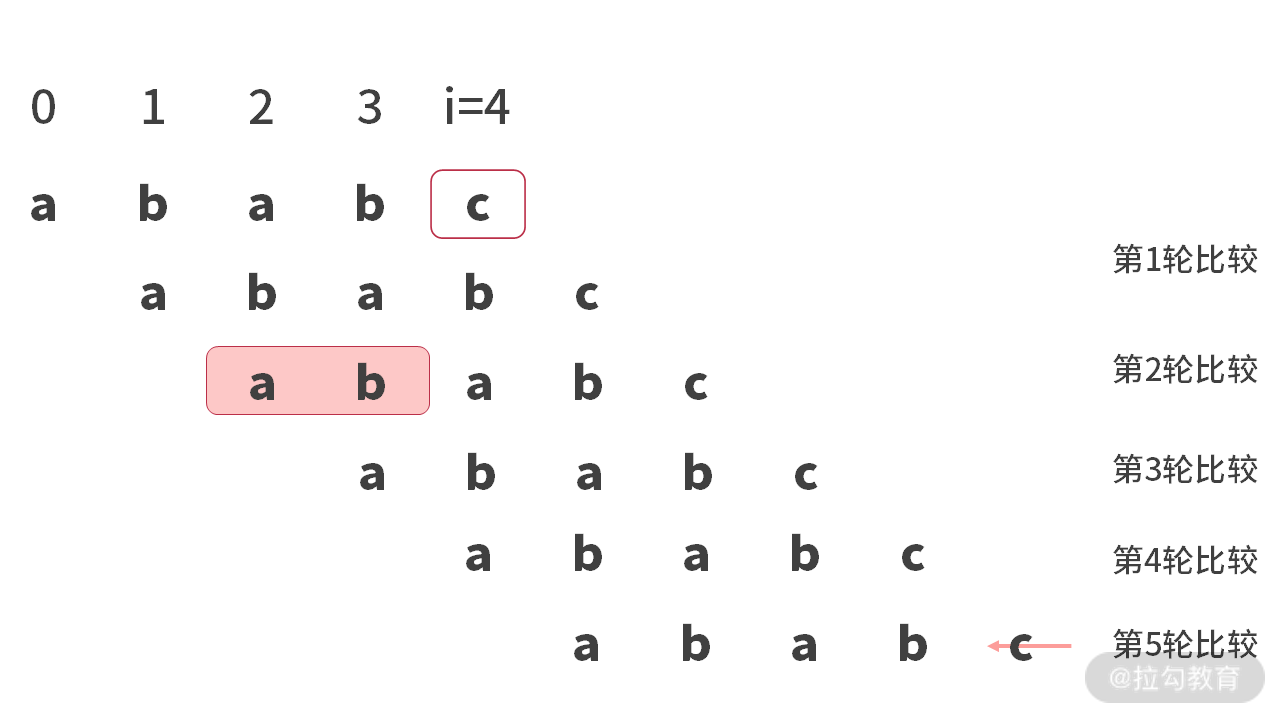
我们很快可以发现，暴力的比较过程，和我们最开始的字符串暴力算法非常类似。

优化暴力算法的思路就是跳过一些无效比较。

第二阶段：跳过无效比较方法 1

那么这里是否可以跳过一些无效比较呢？（提示，借助 PMT 的思路）

很快，我们应该可以发现，在第 2 轮比较的时候，当得到已经匹配的字符串为 “ab” 时，PMT[“ab”] = 0。此时，下一轮比较的时候，应该直接从 j = 0 开始。也就是如下图所示的地方：

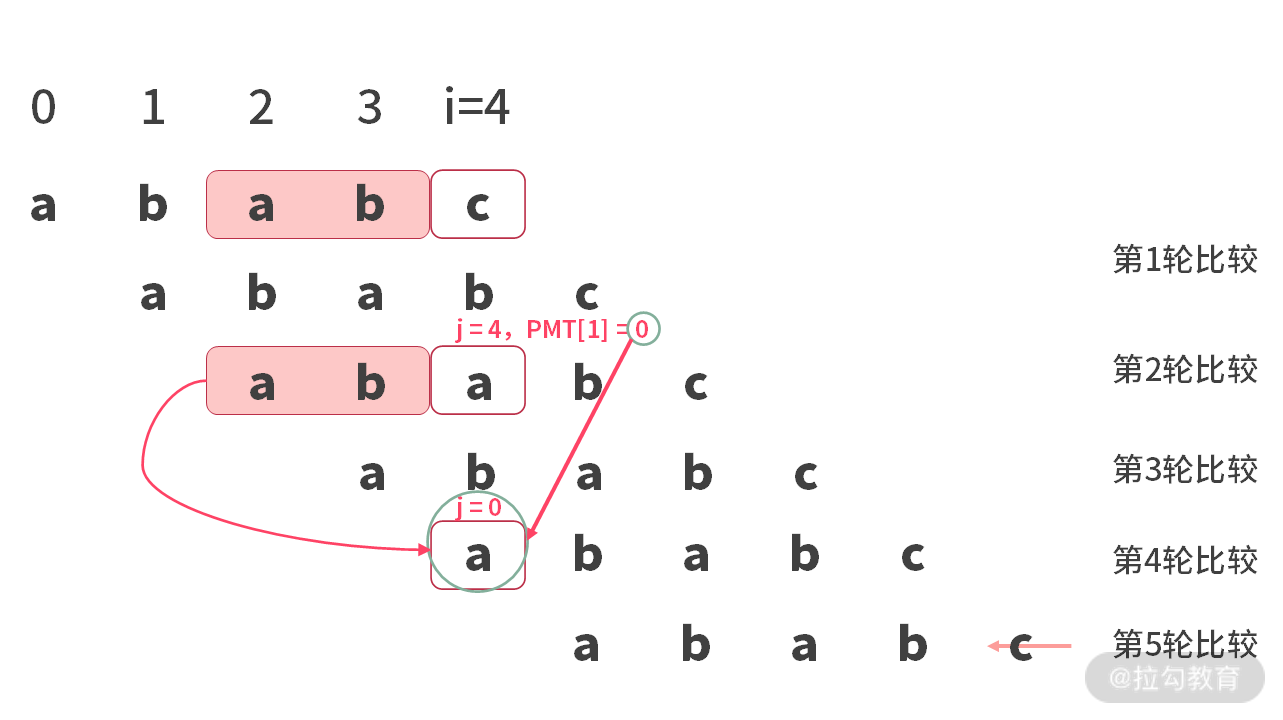
我们可以直接把第 3 轮给跳过。所以当我们计算 PMT[“ababc”] 的时候，需要依赖 P MT[“ab”]。这就形成了一个子问题。

第三阶段：跳过无效比较方法 2

首先我们看一种运气好的情况：

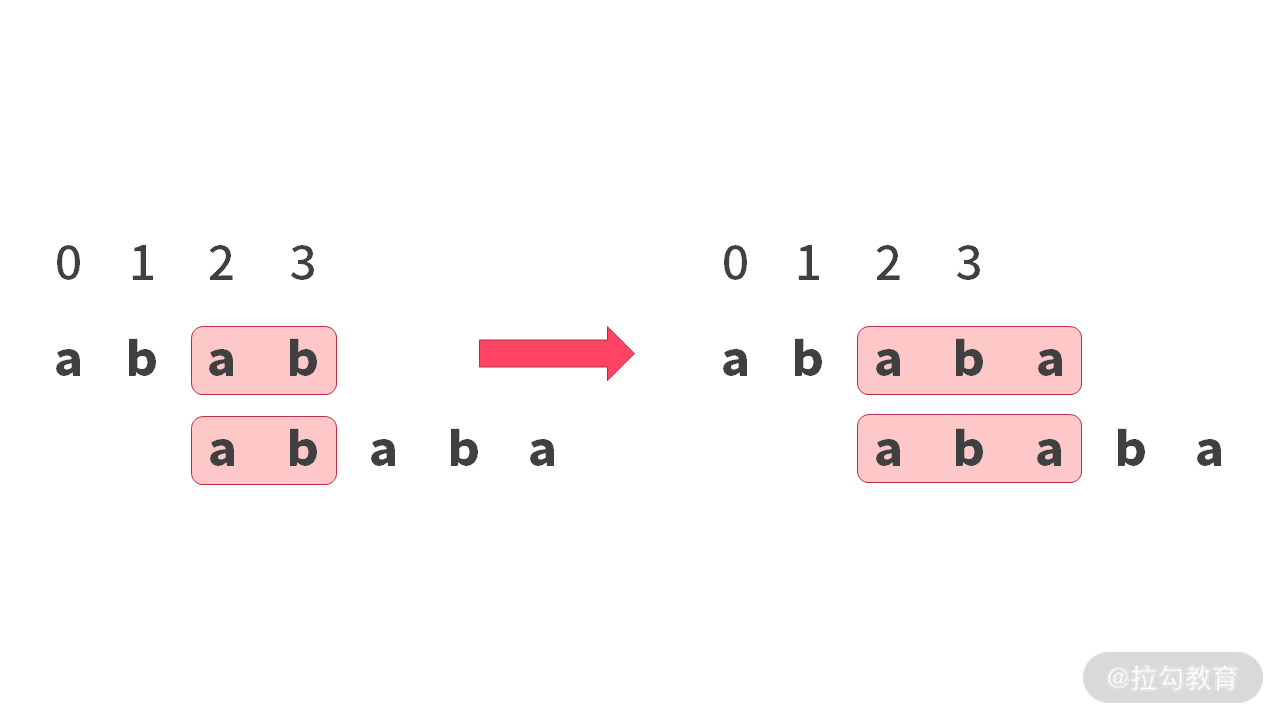
已知：在左边，我们找到了字符串 “abab” 的前后缀的最长匹配“ab”（长度为 2）。那么当我们再去求字符串”ababa” 的前后缀的最长匹配的时候，直接往后延伸一位就可以了。

我们利用反证法进行证明。

• 条件：字符串 “abab” 的前后缀的最长匹配“ab”（长度为 2）成立。
• 并且假设 “ababa”，相比在 “abab” 的基础上直接延伸，还有更长的 “前后缀的最长匹配”。

观察下图展示的结果，假设框中的区域为相等的部分（不管问号存在的这种情况，并且它们是相等的）。

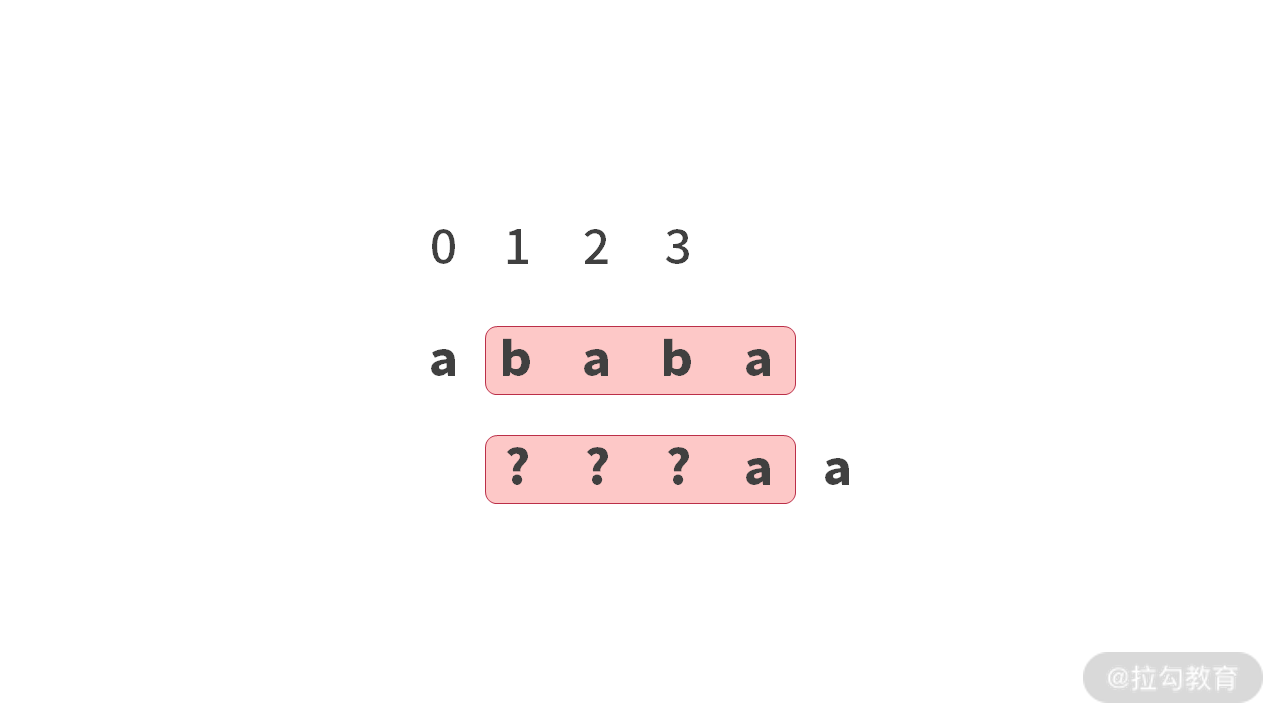
但是，如果存在这种更长的情况。导致的结果就是：绿色线框中的内容肯定是相等的。

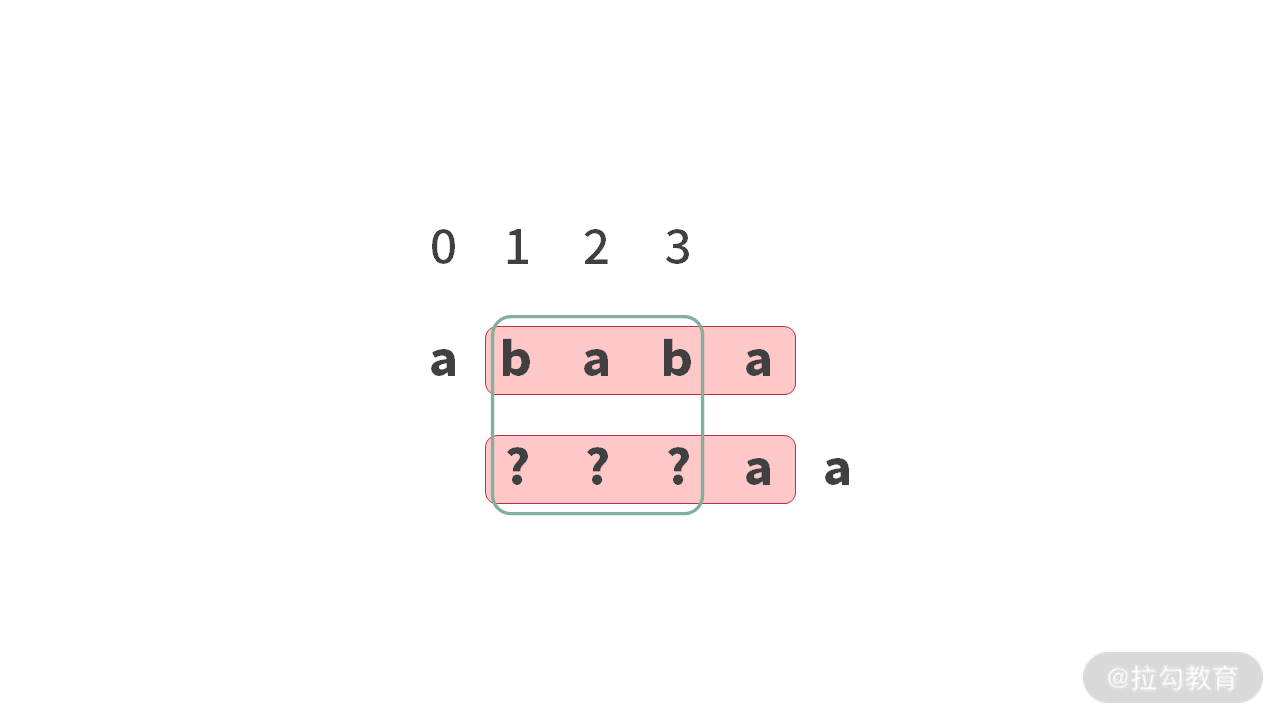
如果绿色线框中的内容相等，那么 “abab” 的前后缀的最长匹配长度就是 3。这样与我们给定的条件矛盾。

实际上，就算是运气差的时候，我们也只需要：直接延伸一位就可以了。这种情况也是可以用完全一样的反证法来证明。那么如下图所示，我们可以把第 1 轮直接跳过。

第四阶段：写代码

我们发现，实际上最后一步的情况只有两种：

• 直接延伸一位，并且延伸之后相等，那么 last_len = 之前匹配的长度 + 1；
• 直接延伸一位，并且延伸之后不相等，那么下一个比较位置就是转到 pmt[j-1]。

但是，我们又发现：每次匹配成功的时候，有如下图所示的这个规律：

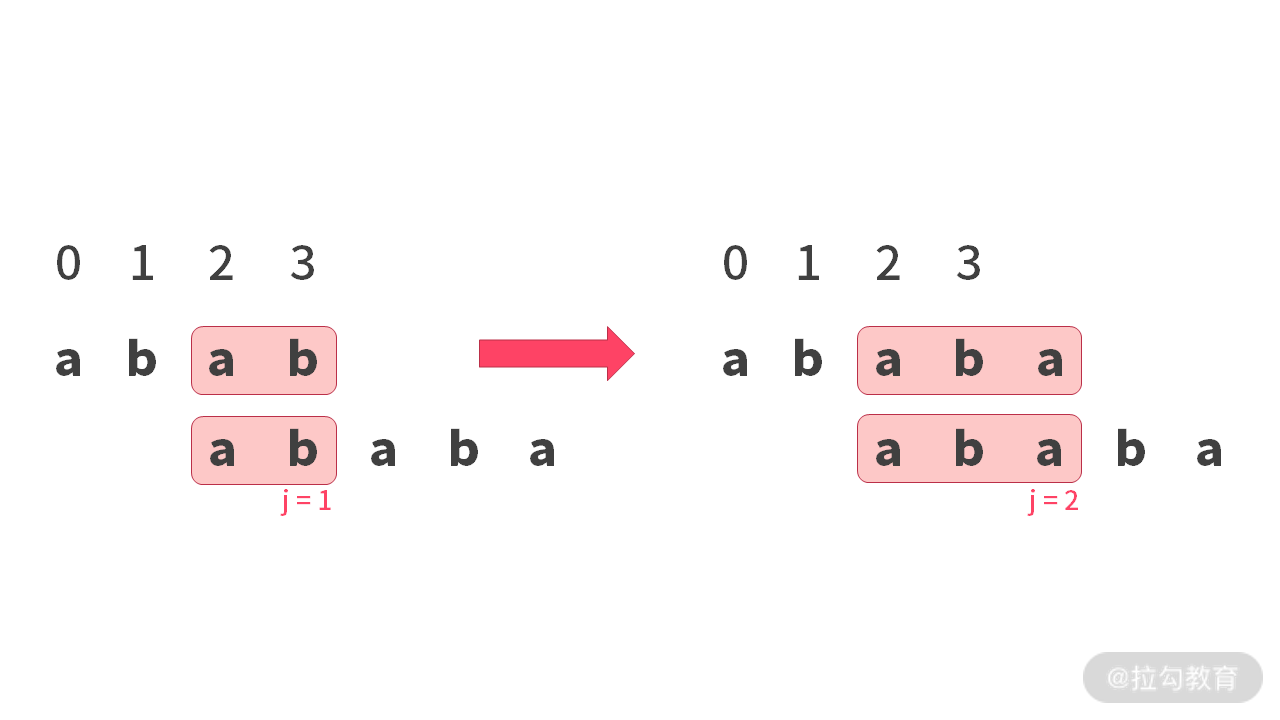
• 左边，需要记录 PMT[“abab”] = 前后缀最长匹配长度 = 2 = j + 1，此时 j = 1；
• 右边，需要记录 PMT[“ababa”] = 前后缀最长匹配长度 = 3 = j + 1，此时 j=2。

匹配失败的时候:

• 1）当 j=0 的时候，j 已经不能再退了，所以需要移动 i；
• 2）当 j > 0 的时候，我们还可以再往回退，于是设置 j = PMT[j-1]。

并且，PMT[x] 里面的所有字符串 x，都是字符串截取了 sub 字符串位置 [0, …, len(x)-1]。由于这个范围的左端点总是 0，所以我们只需要记录这个范围的右端点就可以了，即用 PMT[len(x)-1] 表示 PMT[x]。

那么，我们就可以得到如下代码（解析在注释里）：

int[] buildPMT(String sub) {
final int N = sub == null ? 0 : sub.length();
int[] PMT = new int[N];
int i = 1;
int j = 0;
  PMT[0] = 0;
while (i < N) {
if (sub.charAt(i) == sub.charAt(j)) {
      i++;
      j++;
      PMT[i - 1] = j;
    } else {
if (0 == j) {
        i++;
        PMT[i - 1] = 0;
      } else {
        j = PMT[j - 1];
      }
    }
  }
return PMT;
}

实际上，这部分代码与我们最开始用 PMT 表来求字符串匹配的代码非常像。访问所有 pmt[] 数组里面的元素的时候，都是用 pmt[i-1] 和 pmt[j-1]。每次访问都需要做 1 次减法，当时我们采用的优化方法是：引入 next 数组。那么同样的，这里也可以引入 next 数组。

最终求解 next 数组的代码就可以表示如下：

int[] buildNext(String sub) {
final int N = sub == null ? 0 : sub.length();
int[] next = new int[N + 1];
int i = 0;
int j = -1;
    next[0] = -1;
while (i < N) {
if (j == -1 || sub.charAt(i) == sub.charAt(j)) {
            i++;
            j++;
            next[i] = j;
        } else {
            j = next[j];
        }
    }
return next;
}

注意：由于 next 数组是在 pmt 数组的前面插入了一个 -1。所以，申请数组长度的时候，是字符串的长度 +1。注意写代码的时候不要写错！

练习题 1：求解一个字符串的 pmt[] 数组，本质上是一个动态规划，你能用我们《14 | DP：我是怎么治好 “DP 头痛症” 的？》介绍的动态规划 6 步分析法进行求解吗？

代码：Java/C++/Python

练习题 2：当我们求解了 pmt[] 数组，由于访问 pmt 数组的时候，都是 pmt[i-1] 或 pmt[j-1]，为了优化掉这个减法，你可以把求解 pmt[] 数组的代码，转成输出 next 数组的代码吗？

代码：Java/C++/Python

练习题 3：给定一个非空的字符串，判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母，并且长度不超过 10000。

输入：”abab”

输出：True

解释：可由子字符串 “ab” 重复两次构成。

方法 1 PMT：Java/C++/Python
方法 2 Next：Java/C++/Python
方法 3 同余：Java/C++/Python

完整的 KMP 代码

到此为止，我们已经可以给出完整的 KMP 代码了，如下所示（解析在注释里）：

class Solution {
private int[] buildNext(String sub) {
final int N = sub == null ? 0 : sub.length();
int[] next = new int[N + 1];
int i = 0;
int j = -1;
        next[0] = -1;
while (i < N) {
if (j == -1 || sub.charAt(i) == sub.charAt(j)) {
                i++;
                j++;
                next[i] = j;
            } else {
                j = next[j];
            }
        }
return next;
    }
public int strStr(String main, String sub) {
int i = 0;
int j = 0;
final int alen = main.length();
final int blen = sub.length();
int[] next = buildNext(sub);
while (i < alen && j < blen) {
if (-1 == j || main.charAt(i) == sub.charAt(j)) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
return j == blen ? i - blen : -1;
    }
}

代码：Java/C++/Python

复杂度分析

这里稍微唠叨一下 KMP 的时间复杂度。在比较成功的情况下，i 和 j 都会前进。在比较失败的时候，j 会往回跑（j back），如下图所示：

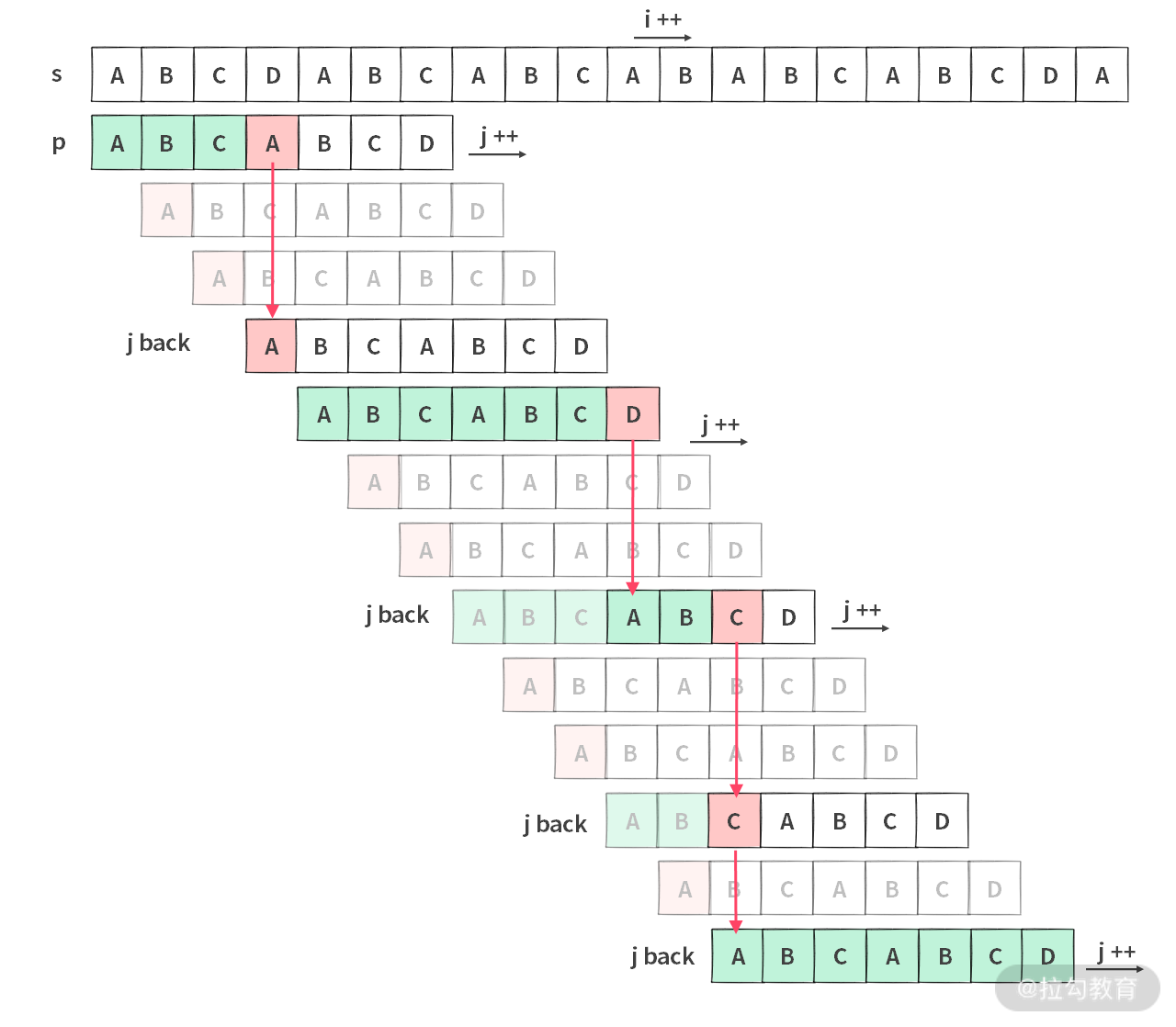
这里我们需要给出两个定义：

• 匹配失败时，当 i 停住不动的时候，称为一个失配点；
• 当遇到一个失配点时，j 会往回跑，那么会有不同的往回跑的步数。

那么时间复杂度可以写成如下：O(N + sum(每个失配点 x 每个失配点 j 往回跑的次数))。那么最差情况如下图所示：

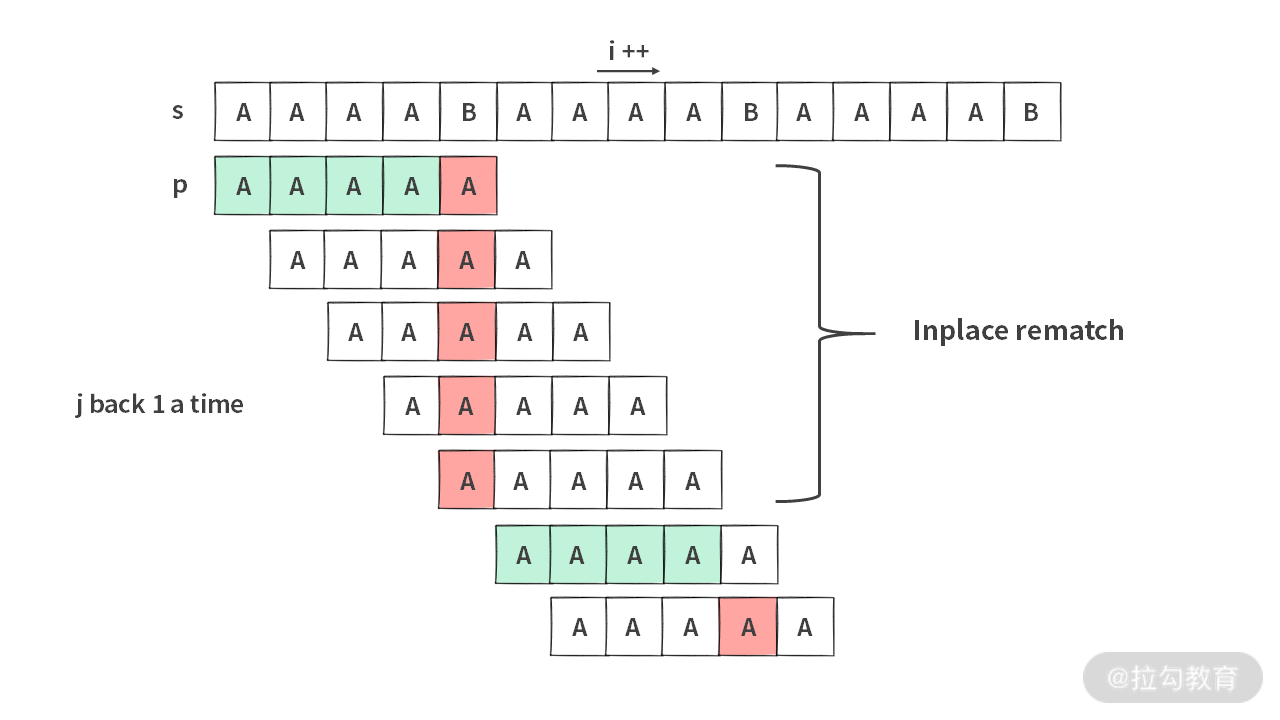
此时失配点只有 N / M 个，每次失配之后，j 要往回跑 M 次。所以最差情况下时间复杂度为 O(N + M)，而空间复杂度为 O(M)。

KMP 的优化

相信你已经理解了前面介绍的 PMT 对暴力算法进行优化的原理，其核心就是跳过无效地比较。那么，我们再看一下，是不是可以在 KMP 的基础上跳过更多的无效比较呢？

假设有如下比较失败的情况：

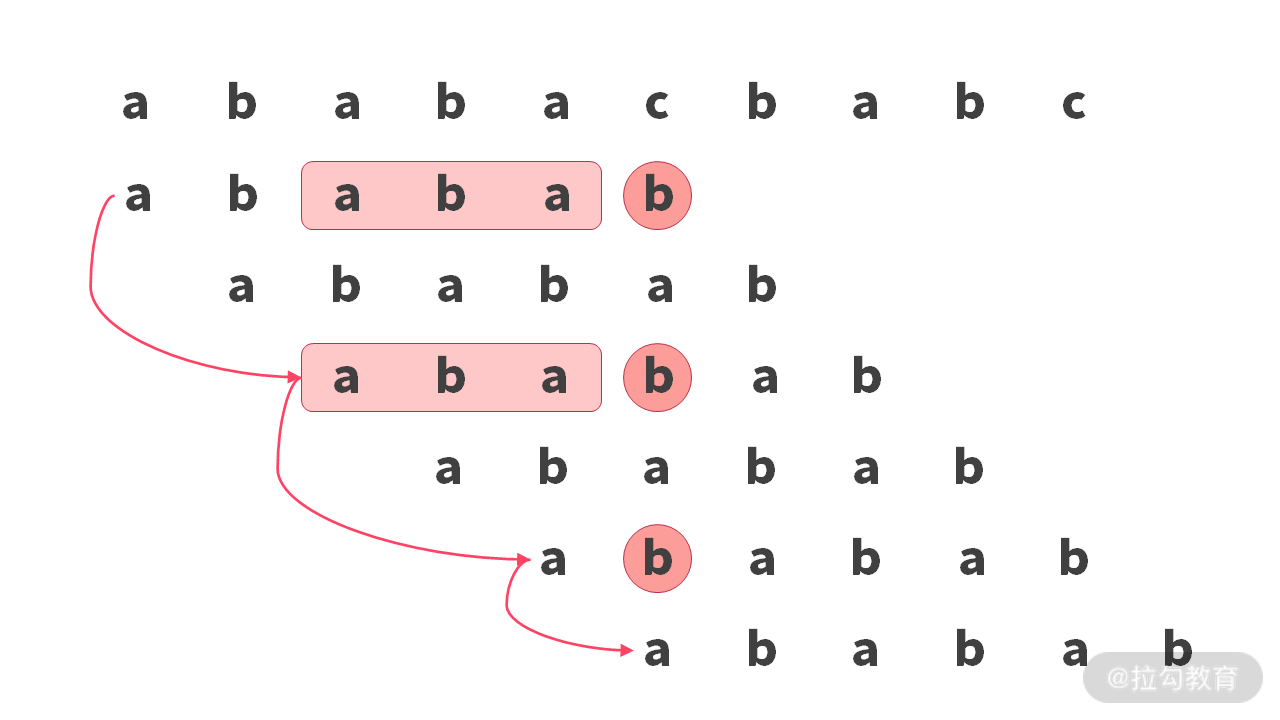
我们已经跳过了比较失败的情况，不过可以发现，每次回退，其实都是反复地用’b’ 和’c’ 字符进行比较。实际这里上可以进行如下优化：

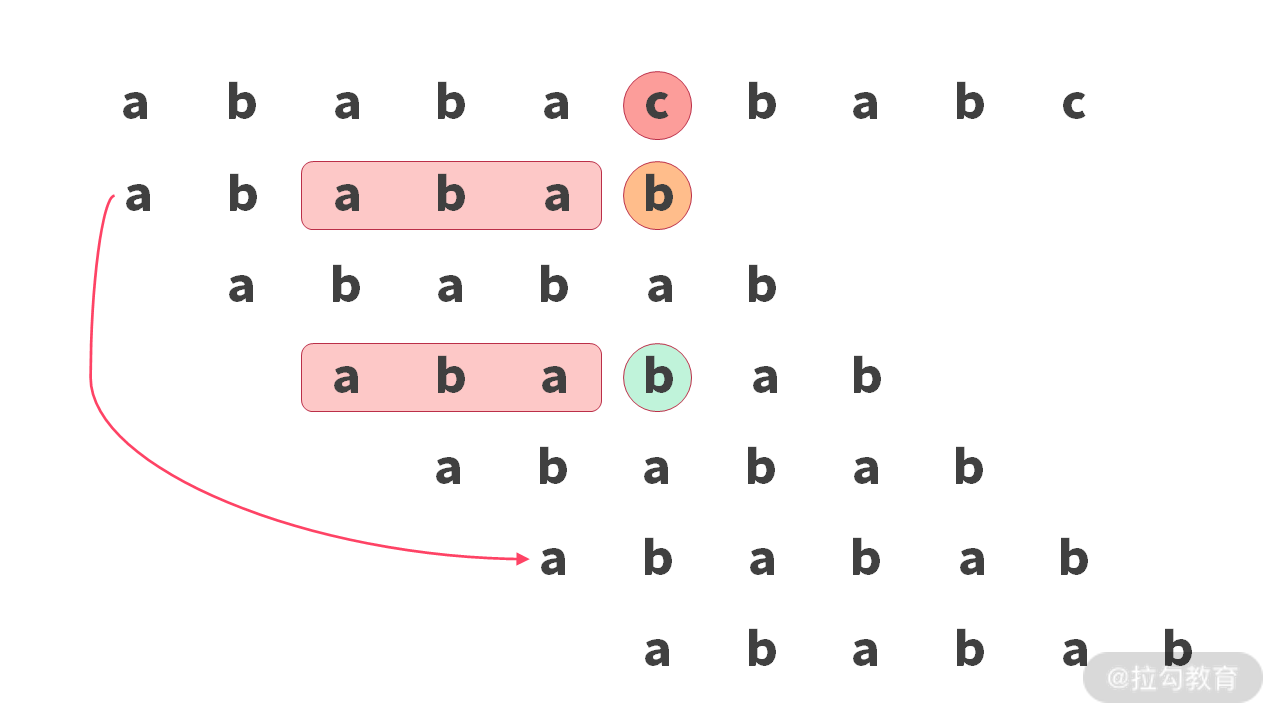
总结一下，当发现回退之后的字符仍然是相等的时候，我们就再回退一次。由于这部分代码只涉及求解 next 数组，所以我把这部分代码也给你写出来：

private int[] buildNext(String sub) {
final int N = sub == null ? 0 : sub.length();
int[] next = new int[N + 1];
int i = 0;
int j = -1;
        next[0] = -1;
while (i < N) {
if (j == -1 || sub.charAt(i) == sub.charAt(j)) {
                i++;
                j++;
if (i < sub.length() && 
                    j < sub.length() &&
                    sub.charAt(i) == sub.charAt(j)) {
                    next[i] = next[j];    
                } else {
                    next[i] = j;
                }
            } else {
                j = next[j];
            }
        }
return next;
    }

代码：Java/C++/Python

BM 算法

虽然 KMP 算法能够取得线性时间复杂度。不过，当你打开任何一个文档编辑器的时候，大部分编辑器的搜索算法并不是基于 KMP 算法来实现的。这里主要有两个原因：

• KMP 算法需要在 main 字符串从头搜索到结尾；
• KMP 算法在跳过一些坏字符的时候，会出现不停回退的情况。

比如，当你利用 KMP 算法进行搜索的时候，会有如下情况：

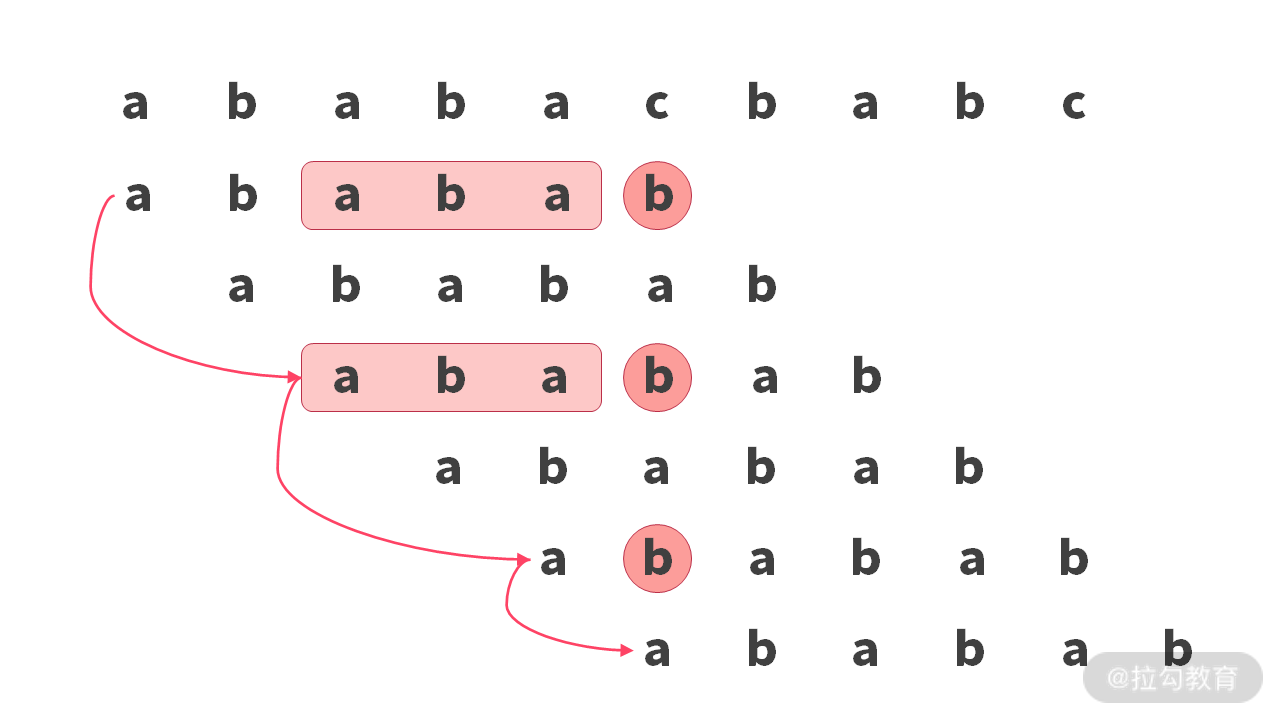
实际上，我们肉眼可见的是，字符’c’ 并不出现在 sub 字符串，所以我们没有必要一直回退。一种更好的办法是：将 sub 字符串推到’c’ 字符的后面。

如果你能想到这个思路，不妨再更进一步思考一下。既然字符串比较的时候，右边失效就直接前移了，那么我们直接从右往左边比较，不是来得更直接吗？

于是，基于下面这两个思路你就可以得到答案。

• 坏字符：在 main 字符串与 sub比较失败的字符；
• 从右向左比较。

有人发明了 BM（Boyer-Moore）算法，还在字符串查找上留下了大名。你先别后悔晚生了那么多年，我们一起再把这个算法讲透。

概念

我会采用 Moore 举的例子一步一步展开介绍。两个字符串为：main = “HERE IS A SIMPLE EXAMPLE”, sub = “EXAMPLE”。

1. 第 1 步

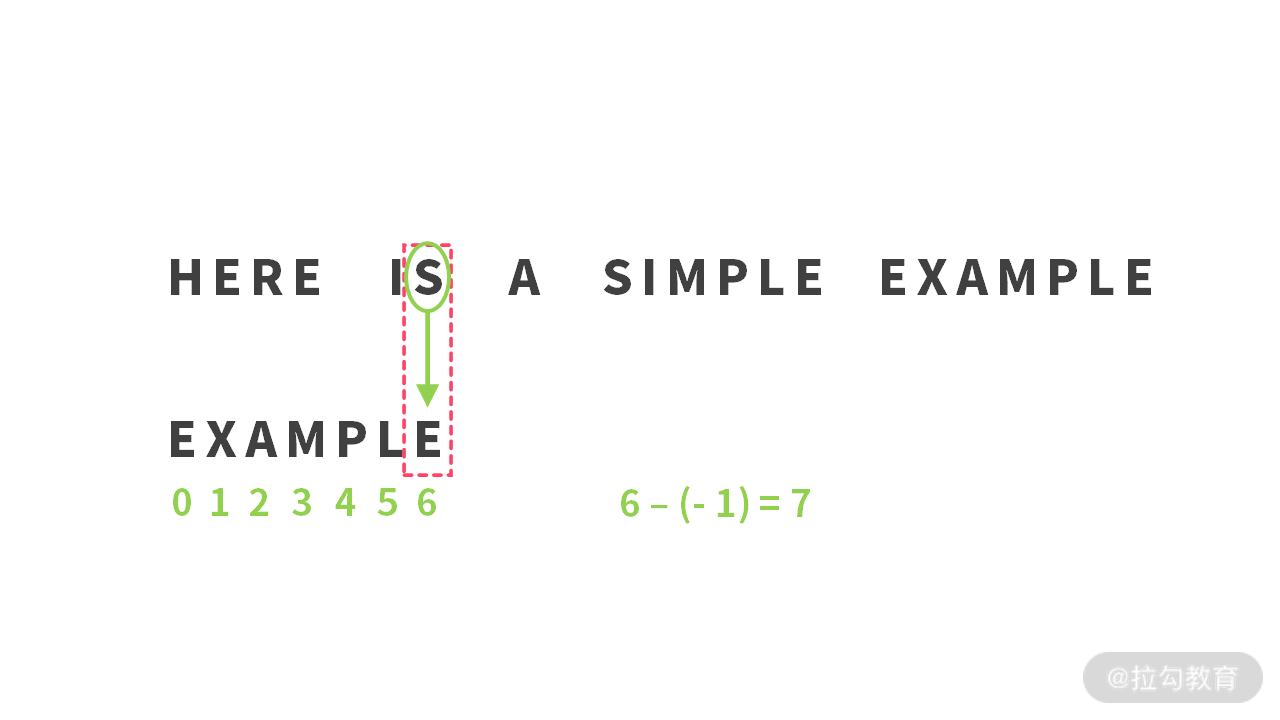
首先比较’S’ != ‘E’，那么需要把 sub 字符串移动到’S’ 的后面。因为’S’ 从来没有出现在 sub 字符串，所以’S’ 就是一个坏字符。

注意：坏字符指的是匹配失败的 main 字符串中对应的那个字符，而不是说没有在 sub 字符串里面出现的字符。

2. 第 2 步

‘P’ != ‘E’，此时’P’ 是一个坏字符，但是出现在 sub 中。那么我们移动 sub 字符串，让两个字符串在’P’ 字符这里对齐，移动的距离为 2。

由第 1 步和第 2 步，可以得到一个 “坏字符” 规则：

当匹配失败的时候，移动距离 = 坏字符的位置 - sub 中的上一次出现位置。

注意：这里 “坏字符的位置” 指的是坏字符在匹配失败的时候，在 sub 字符串中的下标。举 2 个例子：

例 1：在第 1 步比较失败之后，我们移动 7 步。如下图所示：

例 2：在第 2 步比较失败之后，我们移动 4 步。如下图所示：

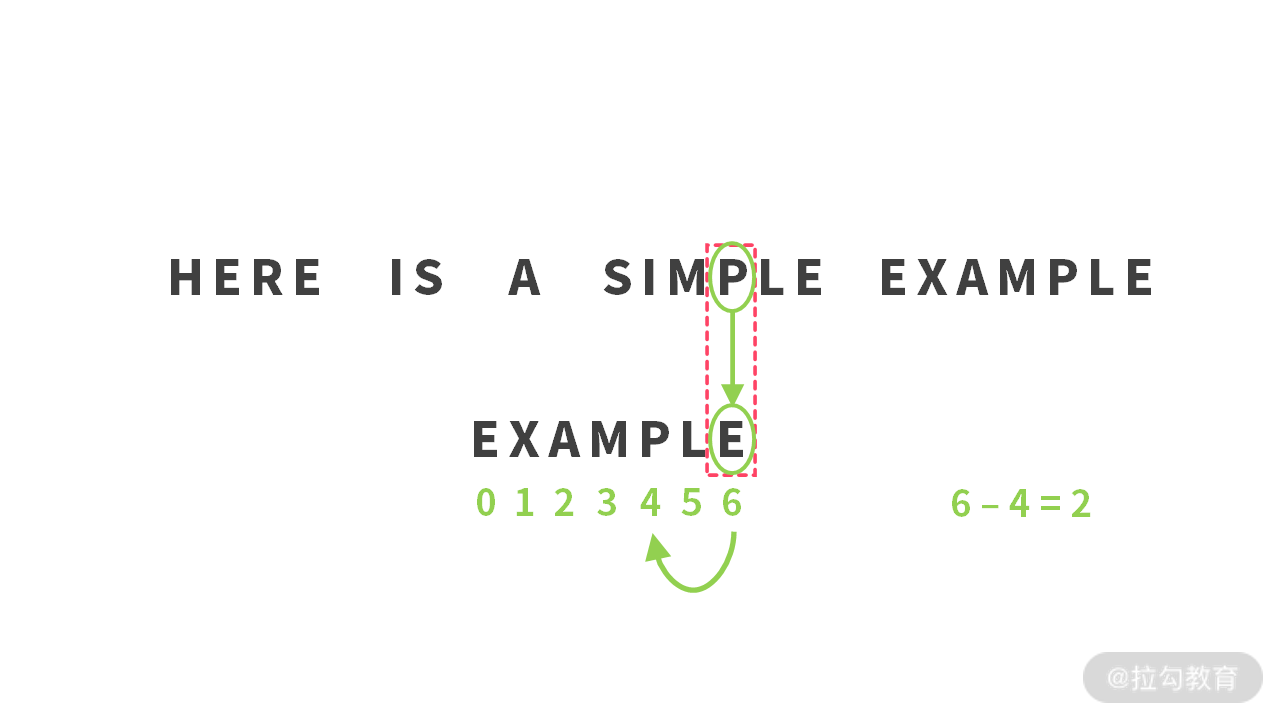
当’P’ != ‘E’ 时，坏字符对应 sub 中的比较位置为 6，而在 sub[6] 之前出现的’P’ 字符下标为 4，所以移动距离为 6 - 4 = 2。

3. 第 3 步

移动之后，我们依然从尾部开始比较。一直向前移动，如下图所示：

由于我们是从后往前进行比较，比较成功的字符串都是位于 sub 字符串的尾部（即后缀），所以可以把这些比较成功的后缀子串称为好后缀（good suffix）。

因此，”E”, “LE”, “PLE”, “MPLE” 都是好后缀。

4. 第 4 步

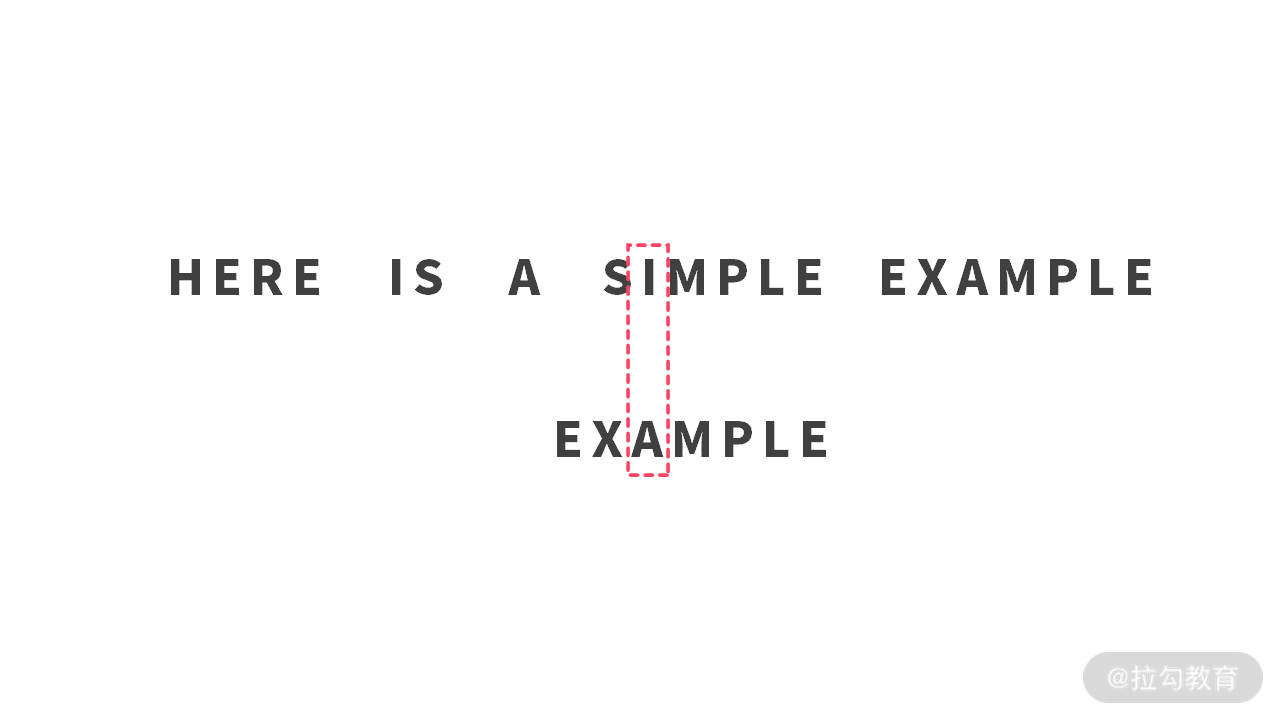
到此时，’I’ 就是一个坏字符，因为比较失败了。此时正在比较 sub[2]，而 sub[0,1] 之前都没有’I’ 字符，所以移动距离为 2 - (-1) = 3。

那么问题是，有没有更好的移动办法？ 这个移动办法其实就在第 5 步。

5. 第 5 步

我先介绍一下思路：在前面的 “坏字符规则” 里介绍了当单个字符匹配失败的时候的移动距离。那么有没有可能把一些 sub 字符串连续的字符，当成一个整体处理呢？

如果你想到了这一点，就得到了 BM 算法的精髓：好后缀规则。这个规则还有以下 3 种情况。

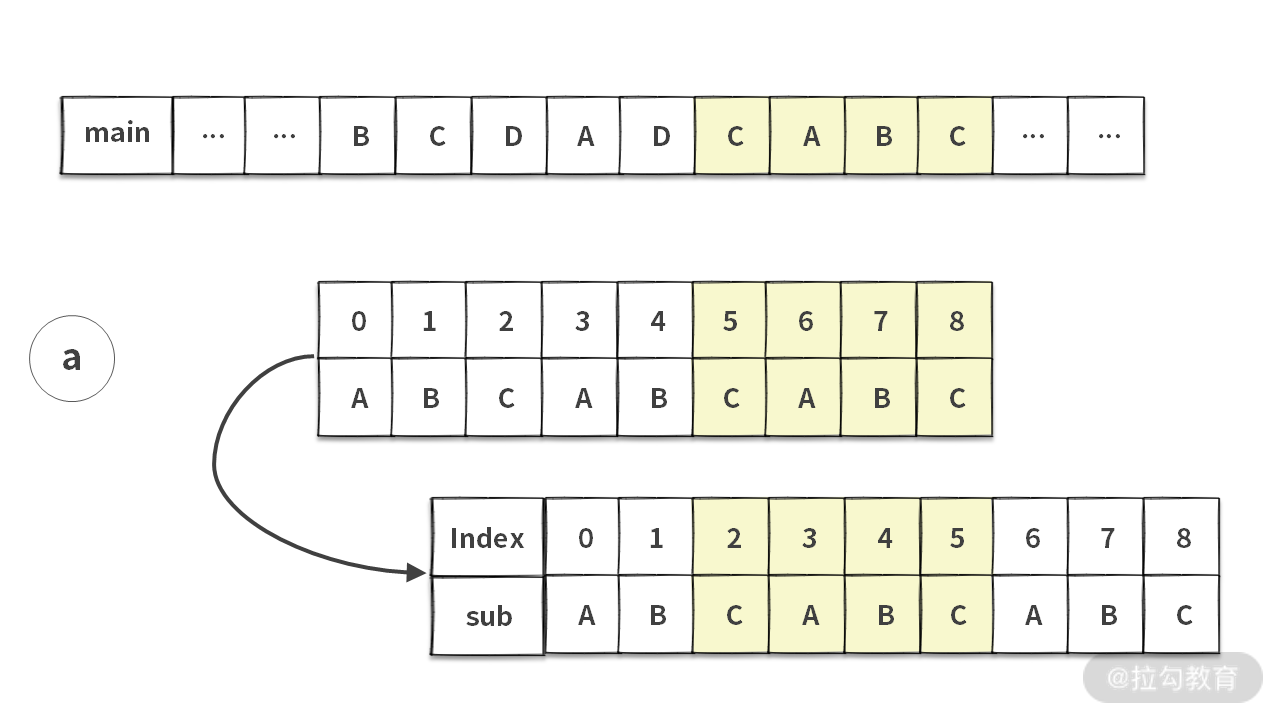
1）如果我们将已匹配连续的字符串看成一个 “整体”，这些整体也出现在 sub 字符串里面，就可以重新进行对齐。如下所示：

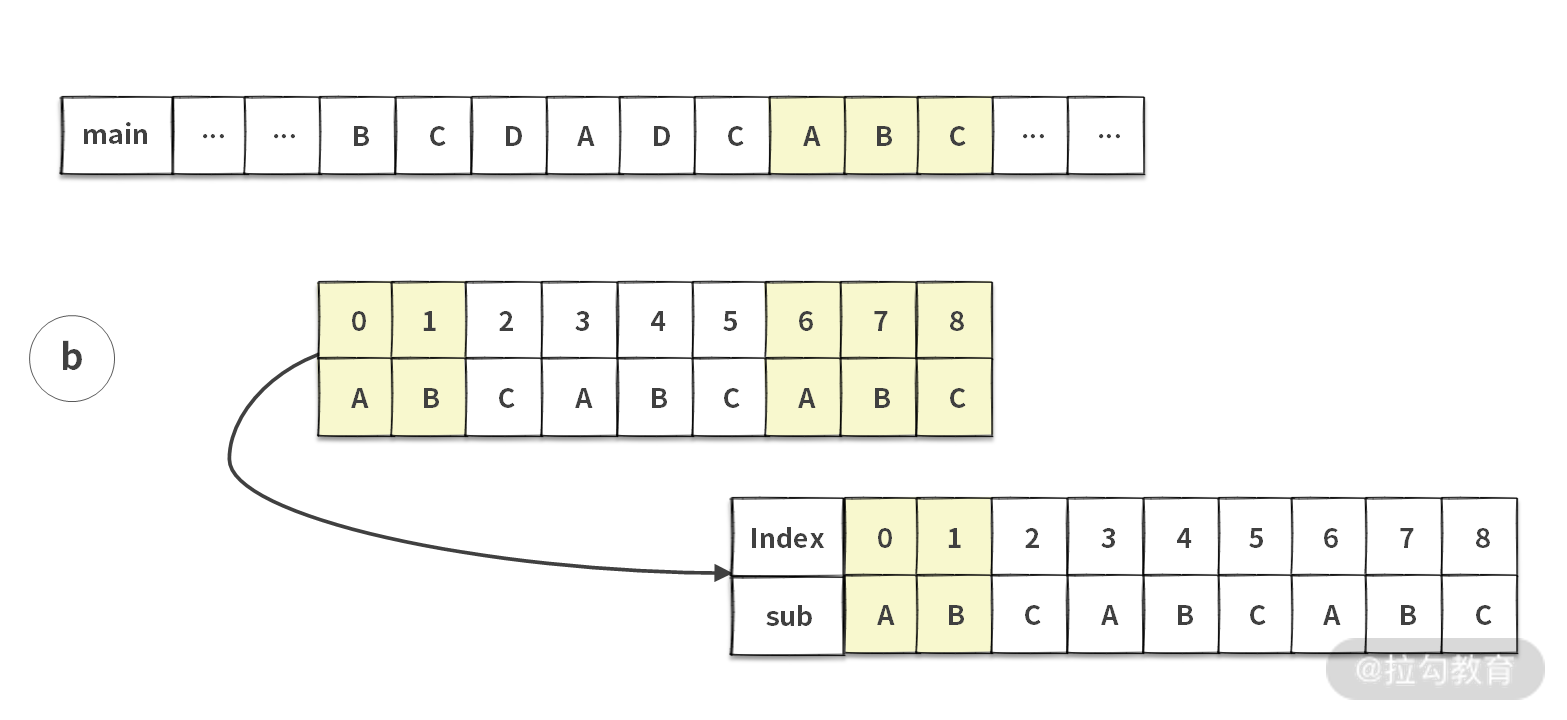
2）如果已匹配字符串的 “好后缀”出现在 sub 的头部，那么只需要重新对齐就可以了。

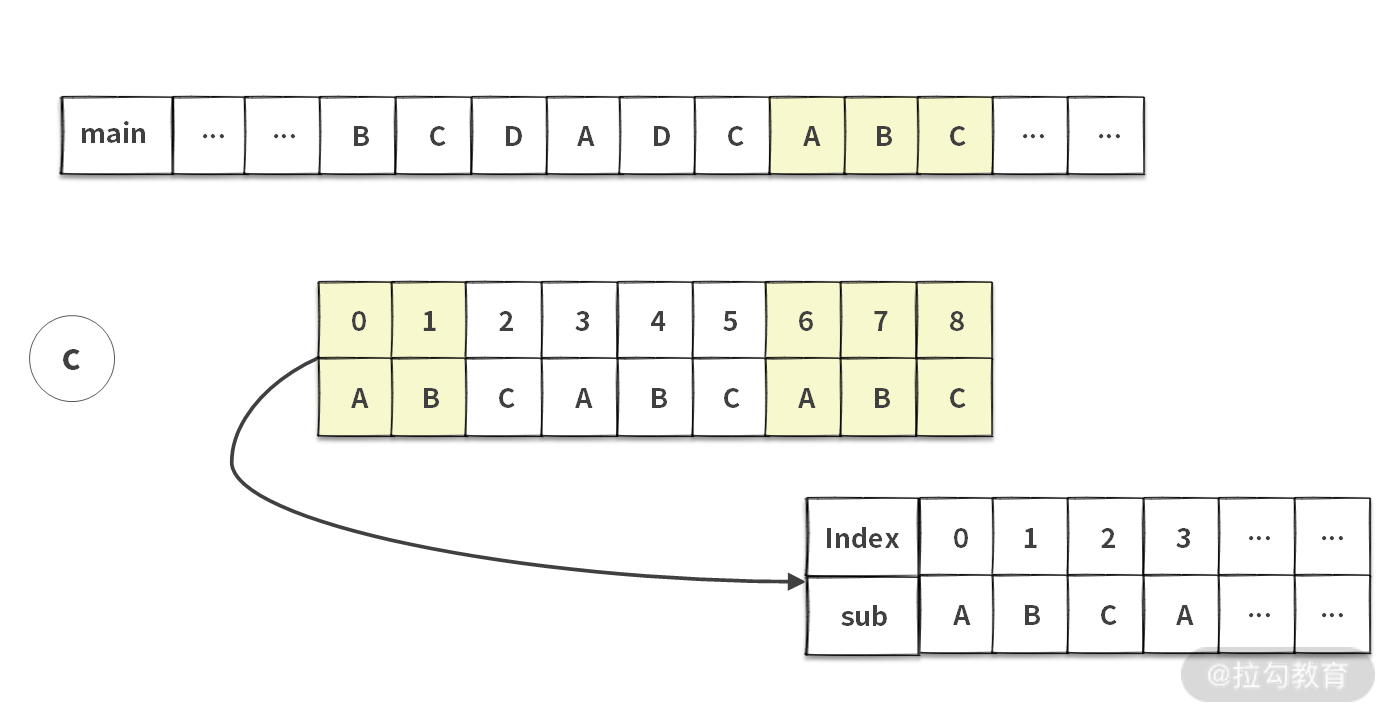
3） 如果 1）2）都不满足，那么直接跳过这段已匹配字符串。

这里我需要特别地说明一下：

• 处理的时候，必须从 1）、2）、3）依次处理；
• 情况 1）只需要出现在 sub 子串中，而情况 2）中的 “好后缀” 必须要是 sub 字符串的前缀；
• 在处理情况 2）的时候，如果有很多个好后缀串，我们总是让 “好后缀” 更长的优先。

再回到例子中，看一下应该如何移动：

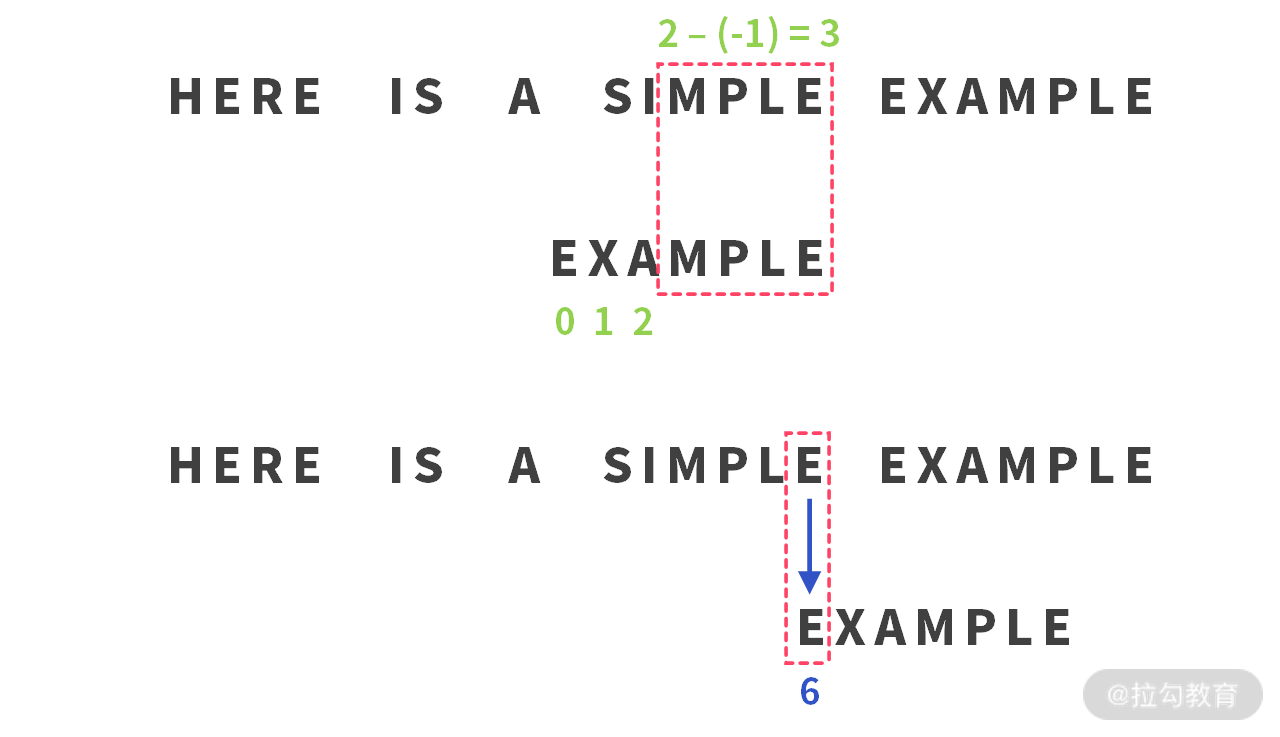
首先根据坏字符规则，因为’I’ != ‘A’，可以得到移动步数为 2 - (-1) = 3。根据好后缀规则，我们再分别看 1）、2）、3）这三种情况：

1）已匹配的字符串为 MPLE，这个字符串没有在 sub 字符串的更左边出现过，所以情况 1）不满足；

2）MPLE 的好后缀有 {“PLE”, “LE”, “E”}，其中只有 “E” 是 sub 字符串的前缀，所以需要移动 6 步将 “E” 对齐；

3）匹配到了 2），所以 3）不需要处理。

我们发现，在第 5 步，当使用 “好后缀规则” 的时候，能够移动更远的距离。所以我们最终选择这个更长的移动距离。

当然，选择 “坏字符规则” 与“好后缀规则”的时候，谁移动的距离更大，我们就用谁。

6. 第 6 步

第 6 步在第 5 步的基础上，只能使用坏字符规则。

因为没有好后缀可供使用。向后移动 6 - 4 = 2 位。

7. 第 7 步

匹配成功！不过，我们在进行编辑器中的文本搜索时，实际上还会继续往后面搜索。

suffix 和 prefix

前面我们介绍了关于坏字符的移动距离的计算，下面再看一下 “好后缀规则” 下的移动距离。这里需要引入两个数组，suffix 和 prefix。我们先看 suffix。

对于 sub = “ABCABCABC” 而言，suffix[4] 表示的含义如下图所示：

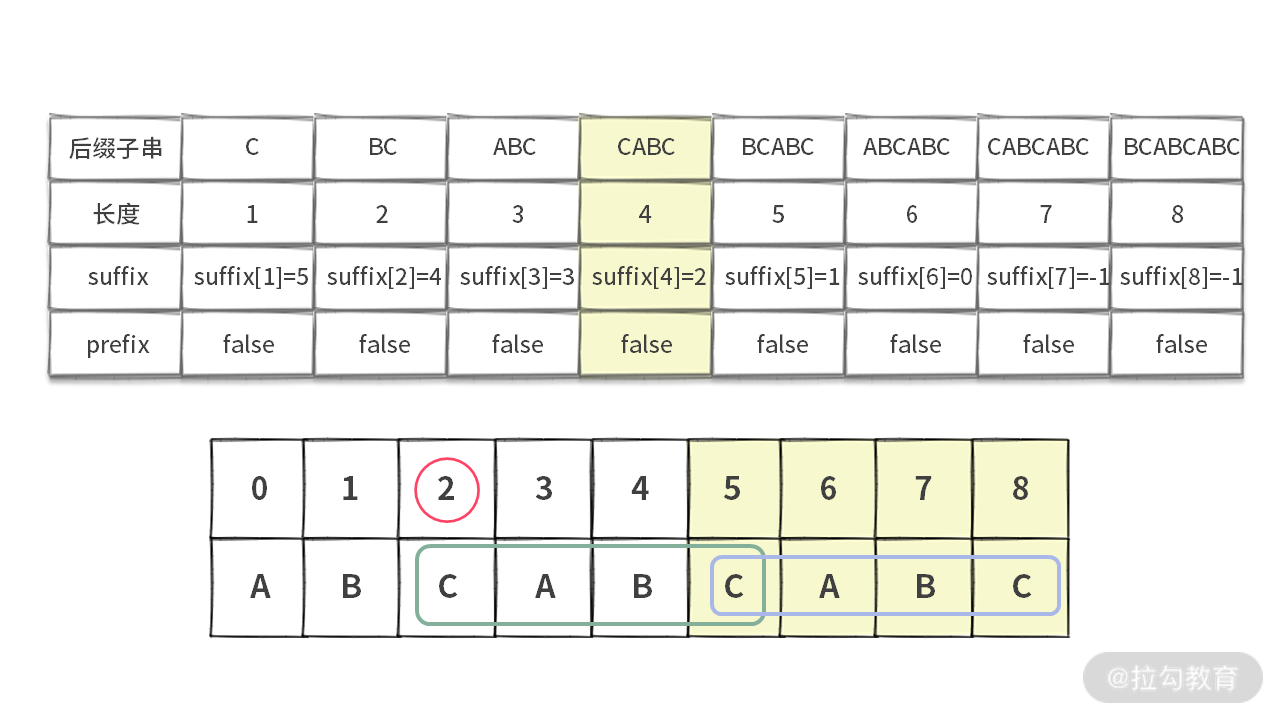
suffix[] 数组下标 i 表示长度为 i 的后缀串。suffix[i] 存放的值，表示在其左边出现相同字符串的最大起始位置。比如：

• sub = “ABCABCABC” 时，对于子串 “CABC” 而言，suffix[4 = len(“CABC”)] = 2，还有一个同样的子串 “CBAC” 出现在 sub 字符串的下标 2 处；
• sub = “BBB” 时，当子串为 “B” 时，suffix[1 = len(“B”)] = 1，对于后缀来说，有两个地方出现了这个子串，即 sub[0] 和 sub[1]，这里我们需要取最大的起始位置1。

而 prefix[i] 数组则表示长度为 i 的后缀串是不是 sub 的前缀。

算法实现

【代码】根据前面的分析，我们可以写出代码如下（代码并不长，只是我加了很多注释）：

class Solution {
static private int[] bad = new int[256];
static private int[] suffix = null;
static private boolean[] prefix = null;
   * 记录每个字符在sub字符串中的出现的最右端的下标位置
   * 如果没有出现，那么设置为-1
   * 用于坏字符规则
   * @param sub
   */
private void buildBadCharPos(String sub) {
for (int j = 0; j < 256; j++) {
      bad[j] = -1;
    }
for (int j = 0; j < sub.length(); j++) {
      bad[(int)sub.charAt(j)] = j;
    }
  }
   * 这个函数负责生成suffix和prefix
   * 这段代码需要仔细读注释
   * @param sub 要在main字符串中查找的字符串sub
   */
private void buildSuffixPrefix(String sub) {
int i = 0;
int j = 0;
int len = 0;
final int n = sub.length();
for (i = 0; i < n; i++) {
      prefix[i] = false;
      suffix[i] = -1;
    }
for (i = 0; i < n - 1; i++) {
      j = i;
      len = 0;
while (j >= 0 && sub.charAt(j) == sub.charAt(n - 1 - len)) {
        len++;
        suffix[len] = j;
        j--;
      }
if (-1 == j) {
        prefix[len] = true;
      }
    }
  }
   * @param j
   *   sub字符串和main字符串从后往前匹配的时候，在sub[j]位置与main匹配失败
   *   也就是说: sub[j+1,...,n)都和main字符串匹配成功了，是一个好后缀
   * @param n sub字符串的长度
   * @return 依次使用1), 2), 3)返回相应的值
   */
private int moveBySuffixPrefix(int j, int n) {
int len = n - (j + 1);
if (suffix[len] != -1) {
return j + 1 - suffix[len];
    }
for (int r = j + 2; r <= n - 1; r++) {
if (prefix[n - r]) {
return r;
      }
    }
return n;
  }
public int strStr(String main, String sub) {
if (sub == null || sub.length() == 0) {
return 0;
    }
if (main == null || main.length() == 0) {
return -1;
    }
     buildBadCharPos(sub);
final int mainLen = main.length();
final int subLen = sub.length();
     suffix = new int[subLen];
    prefix = new boolean[subLen];
     buildSuffixPrefix(sux);
int i = 0;
int j = 0;
while (i <= mainLen - subLen) {
for (j = subLen - 1; j >= 0; j--) {
if (main.charAt(i + j) != sub.charAt(j)) {
break;
        }
      }
if (j < 0) {
return i;
      }
int badMoveLength = j - bad[(int)main.charAt(i + j)];
int goodSuffixMoveLength = 0;
if (j < subLen - 1) {
goodSuffixMoveLength 
moveBySuffixPrefix(j, subLex);
      }
      i += Math.max(badMoveLength, goodSuffixMoveLength);
    }
return -1;
  }

代码：Java/C++/Python

复杂度分析：时间复杂度，由于需要预处理 sub 字符串得到 suffix 和 prefix，这里的复杂度为 O(M2)。最差情况下，时间复杂度会下降到 O(N×M)。空间复杂度为 O(M)。不过对于无周期的模式串，大部分时间复杂度为 O(N)。其中 N 表示 main 字符串的长度，M 表示 sub 字符串的长度。

【小结】这里我们引入了 BM 算法的一些概念，以及如何从右向左查找的时候进行优化。虽然 BM 算法最差情况下时间复杂度会掉到 O(N×M)，不过再加入一些优化，还是可以将这个算法更改为 O(N) 的线性算法。优化的具体细节，你可以阅读Turbo-BM 算法。

Sunday 算法

Sunday 算法应该是除了暴力算法中最好懂的字符串匹配算法了（不过它在最差情况下是时间复杂度是 O(N×M)，看来跑得快的算法都需要 “挠头发”）。

思路与步骤

我们直接做个让你一看就懂的演示。首先假定字符串为 main = “substring searching” 中查找 sub = “search”。下图中 m 表示的是 sub 字符串的长度。

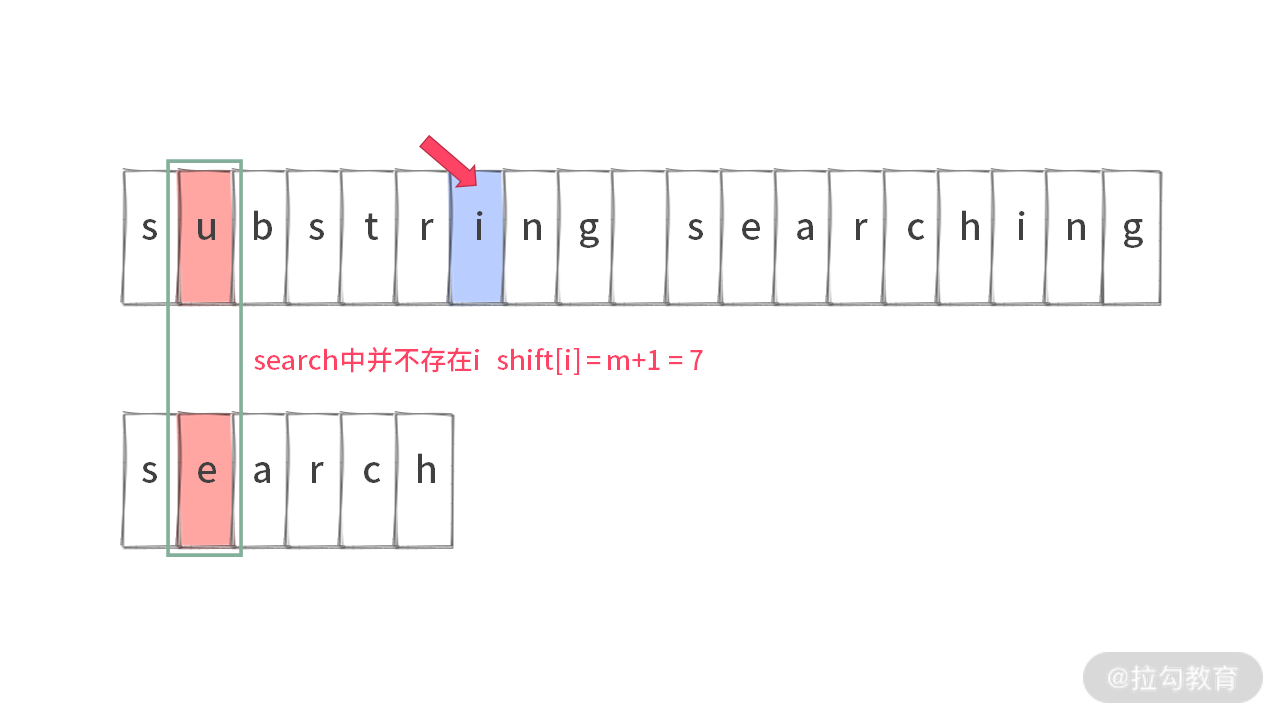
匹配失败的时候，直接看 main 字符串对齐之后，紧接着的那个字符。比如当’u’ != ‘e’ 的时候，立马去看字符’i’，我们称为Target Char。

由于 sub 中不存在字符 i，所以会移动 7 步（下面我们讲这个步数的计算）。

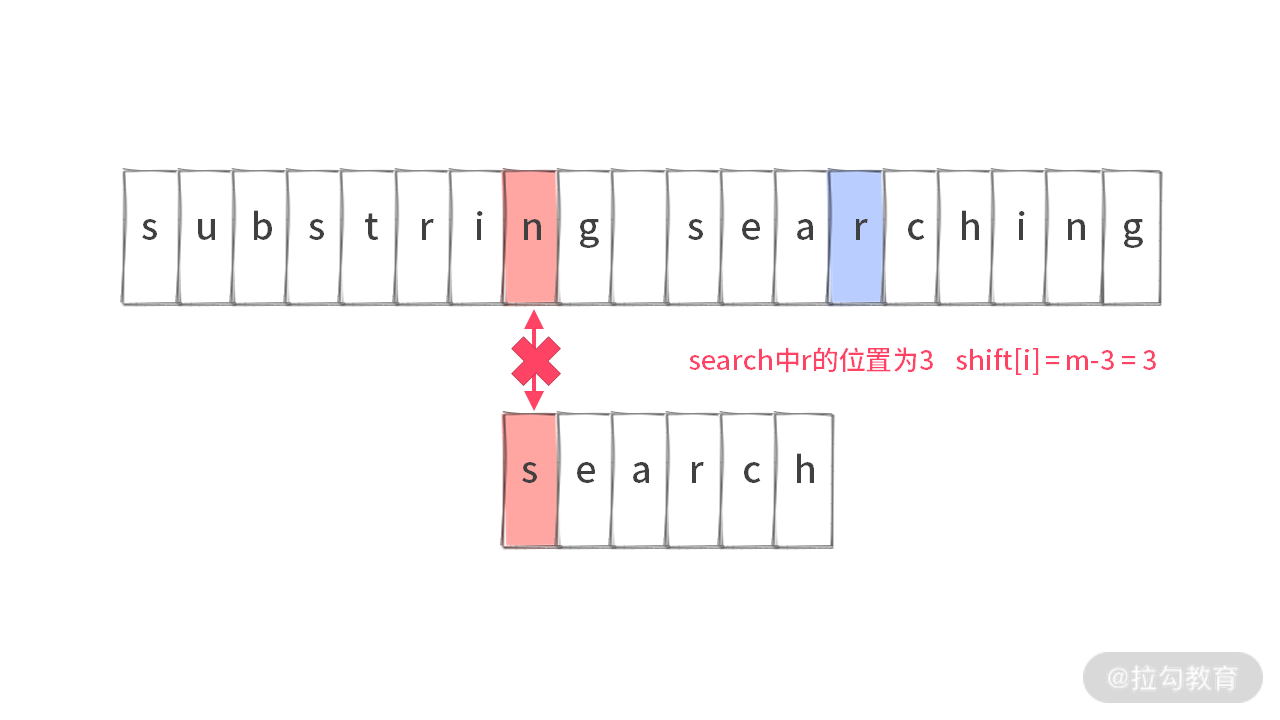
再接着比较’n’ != ‘s’，那么会去看Target Char字符’r’，而’r’ 字符在 search 中的位置为 3。

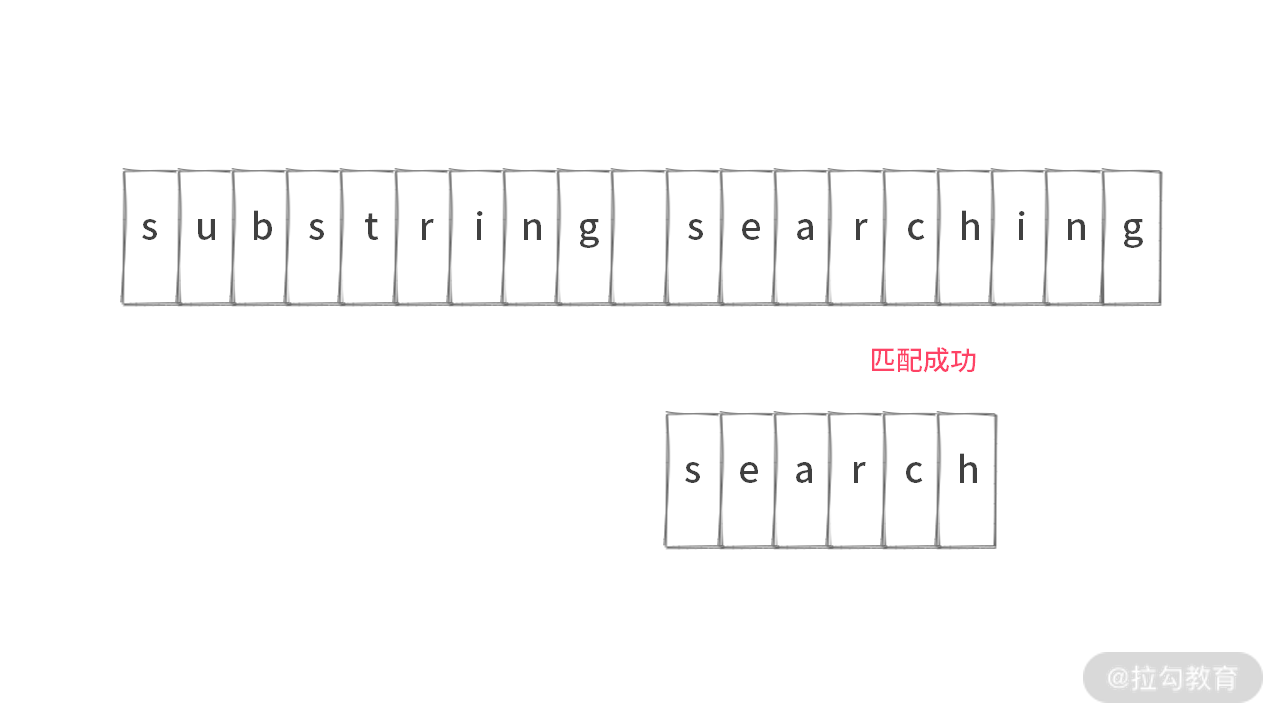
经过再次移动，匹配成功。

移动规则

匹配失败时，只需要向前移动 i + = sub.length() - lastPos[Target Char]。这里 lastPos[] 数组记录的是 sub 字符串中每个字符在 sub 最右边的位置。如果字符没有在 sub 中出现，则标记为 -1。

【代码】至此，我们就可以写出如下代码了（解析在注释里）：

class Solution {
static private int[] pos = new int[256];
public int strStr(String main, String sub) {
if (sub == null || sub.length() == 0) {
return 0;
        }
if (main == null || main.length() == 0) {
return -1;
        }
final int mainLen = main.length();
final int subLen = sub.length();
int i = 0;
int j = 0;
for (j = 0; j < pos.length; j++) {
            pos[j] = -1;
        }
for (j = 0; j < subLen; j++) {
            pos[(int)sub.charAt(j)] = j;
        }
while (i <= mainLen - subLen) {
            j = 0;
while (main.charAt(i + j) == sub.charAt(j)) {
                j++;
if (j >= subLen) {
return i;
                }
            }
if (i + subLen >= mainLen) {
return -1;
            }
final int targetChar = (int)main.charAt(i + subLen);
            i += subLen - pos[targetChar];
        }
return -1;
    }
}

代码：Java/C++/Python

复杂度分析：时间复杂度为 O(N×M)，其中 N 为 main 字符串的长度，M 为 sub 字符串的长度。空间复杂度为 O(256)。

【小结】除了暴力算法，Sunday 算法应该是最好写的算法了。不过实现代码的时候，你仍需要注意两个地方：

• 主循环中 while (i <= mainLen - subLen)，如果取 i < mainLen - subLen，那么无法处理 strStr(“a”, “a”) 这种查找；
• 在取 target char 的时候，需要注意判断是不是越界。

总结

为了方便你复习，我把本讲重点介绍的知识点整理在一张思维导图里：

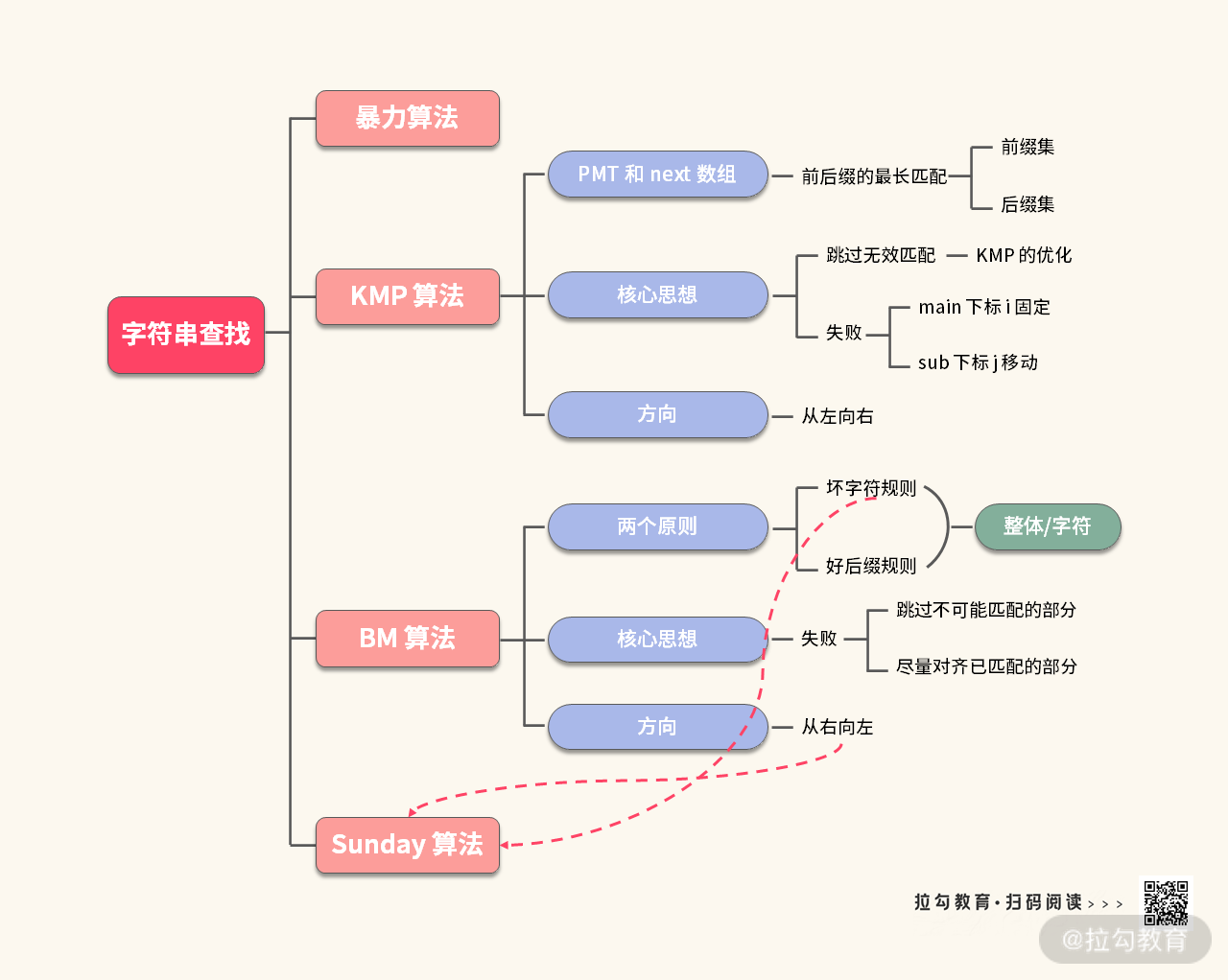
学完本讲，我希望你可以思考一下，是哪些基础知识点导致你对算法没有清晰地理解。然后对照着上图，进行重点突破。

比如，你发现看不懂 KMP 算法的时候，可以查一下，是不是 PMT 的用途没有看懂？看不懂 BM 算法的时候，是不是因为没有弄明白坏字符规则与好后缀规则。

思考题

最后我还给你留了一个思考题。

思考题：给定一个字符串 s，你可以通过在字符串前面添加字符将其转换为回文串。找到并返回可以用这种方式转换的最短回文串。

输入：s = “aacecaaa”

输出：”aaacecaaa”

代码 :Java/C++/Python

我们的字符串查找算法就讲到这里了，接下来我们将要介绍 16 | 如何利用 DP 与单调队列寻找最大矩形？让我们继续前进。