数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
在上一讲中,我给你介绍了解决链表问题的 “三板斧” 中的第一斧:假头,你知道了带假头的链表一共有 6 种基本的操作,分别是初始化、追加结点、头部插入结点、查找结点、插入指定位置之前和删除结点。
如果说三板斧的第一斧平平淡淡,大巧不工;第二斧就是鬼斧神工,生成新链表后,链表的交换、反转求解都会变得极其简单 ;第三斧则是奇思妙想,双指针(也叫快慢指针)用在链表上经常可以解决一些单个指针难以解决的问题。学会了这两种思路,算法面试中的链表题就如同探囊取物了。
注:大部分链表题主要考查动手能力,因此在本讲将不再按照 “分析四步法” 进行讲解。
三板斧的第二斧:新链表
做链表的反转、交换等操作时,我不建议直接在原来的链表上进行操作。一种可取的思路是,把这些操作想象成要生成新的链表,然后借助这些新的链表,完成原本比较复杂的操作。这个方法就是我们今天要讲的“第二斧”——新链表。
接下来,我将采用这种新思路,带你解决一些面试中经常会遇到的疑难题目。
例 1:链表反转
【题目】输入一个链表的头结点,反转该链表,并返回反转后链表的头结点。
输入:1->2->3
输出:3->2->1
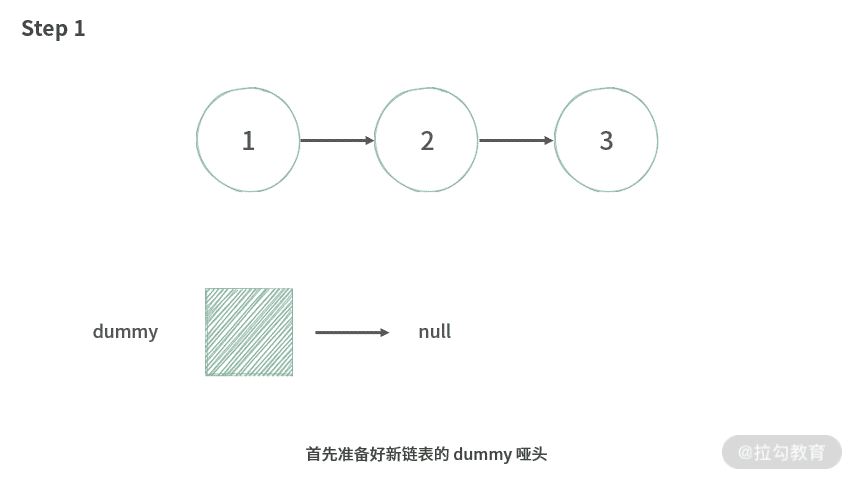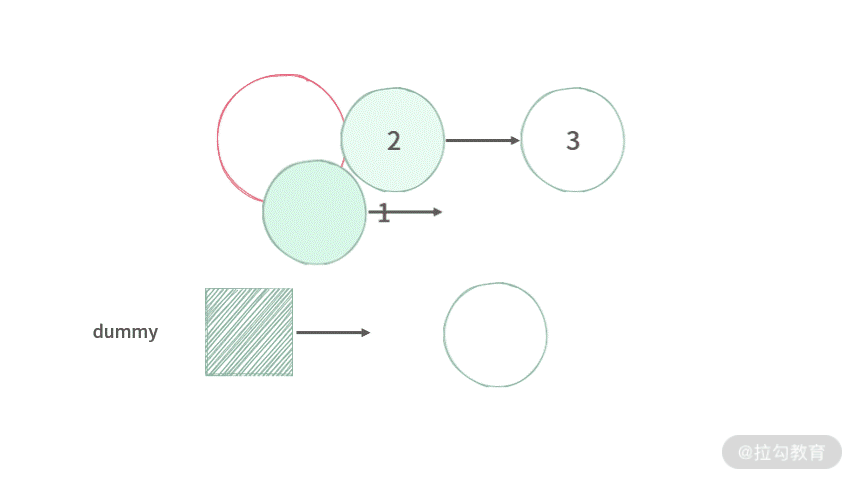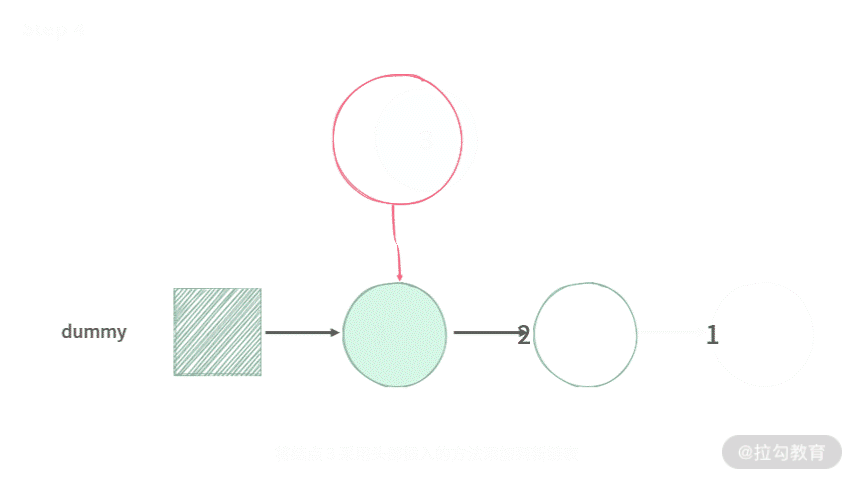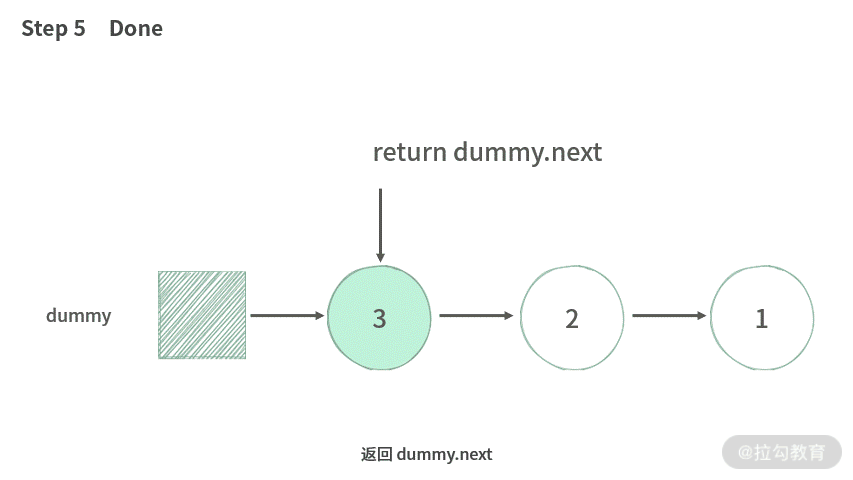
【分析】这里借助假头和新链表求解,思路如下:
- 建立一个新的带假头的空链表;
- 遍历旧链表,依次取出旧链表中的每个结点;
- 采用头部插入的方法放到新链表中;
- 返回 dummy.next。
【画图】这里我们利用示意图演示如下:
【代码】对应的代码如下(解析在注释里):
class Solution {public ListNode reverseList(ListNode head) {ListNode dummy = new ListNode();while (head != null) {ListNode tmp = head.next;head.next = dummy.next;dummy.next = head;head = tmp;}return dummy.next;}}
复杂度分析:每个结点只遍历一次,所以时间复杂度为 O(N),内存空间只使用了常量空间,因此空间复杂度为 O(1)。
【小结】仔细查看代码之后,链表反转的考点就是之前我们学到的基本操作:假头,头部插入法,再结合今天学习的新链表的思路。可以总结如下:
例 2:删除结点
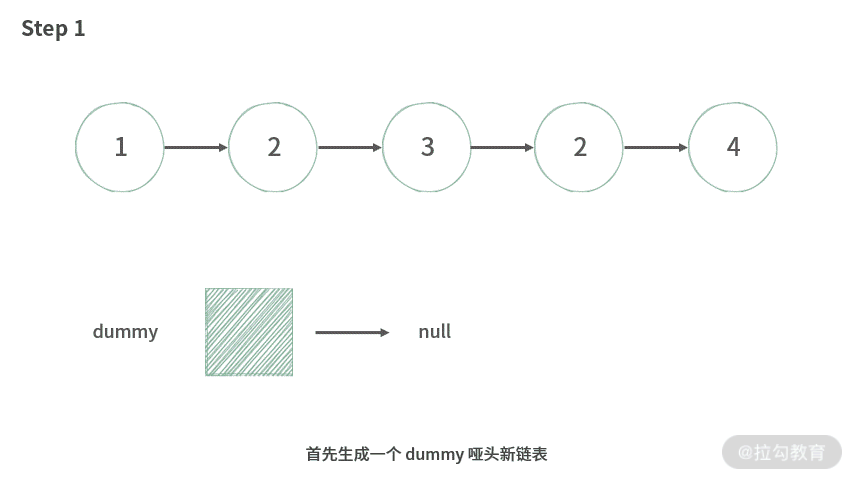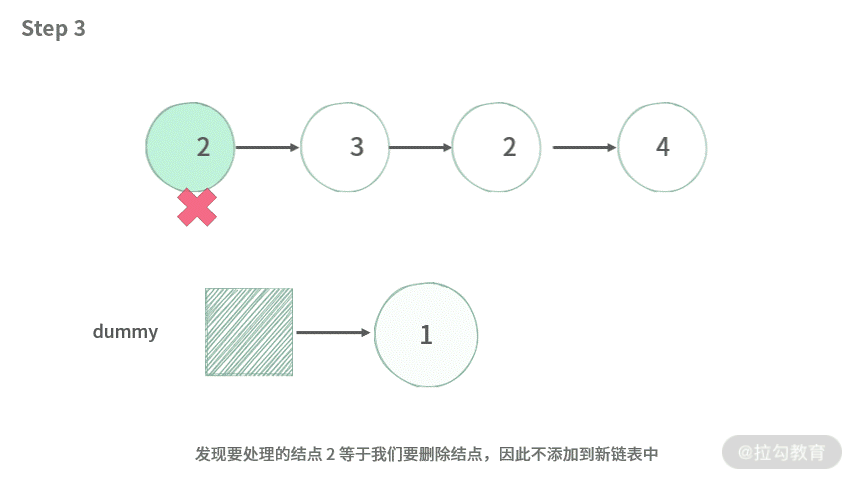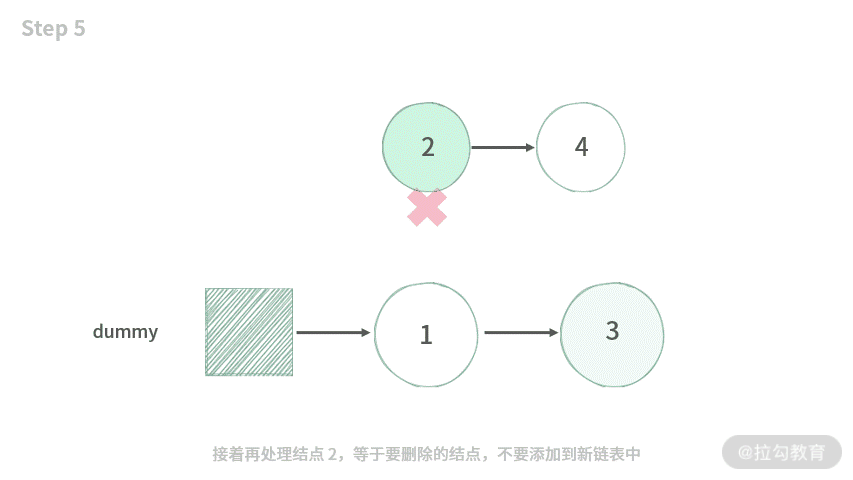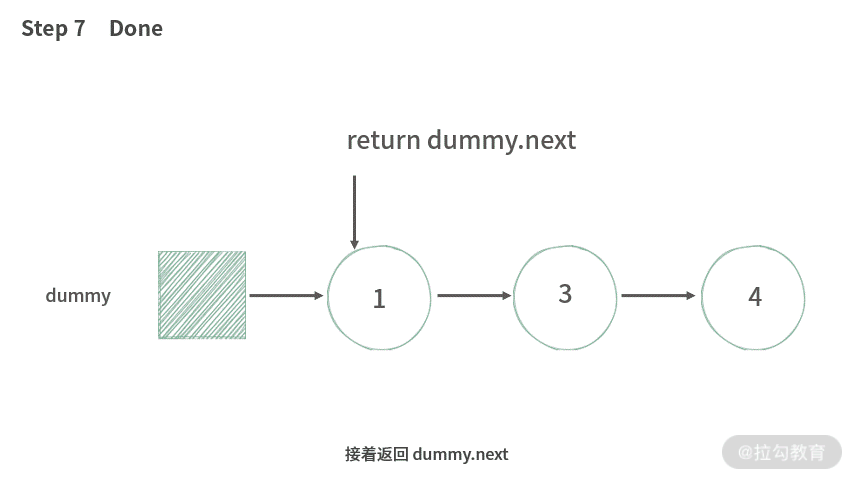
【题目】给定一个链表头及一个整数值,要求把链表里面等于整数值的结点都从链表中移除出去。
输入:1->2->3->2->4, remove = 2
输出:1->3->4。
解释:要移除的整数值是 2。那么移除之后,返回的结果应该是 1->3->4。
【分析】这里我们不采用在原来的链表上进行删除的办法,而是采用新链表的操作思路:
- 建立一个新的带假头的空链表;
- 遍历旧链表,依次取出旧链表中的每个点,如果不删除这个结点,那么就采用尾部插入方法接到新链表中。
可以发现,在这里没有出现结点交换的操作。采用新链表的思路,避免了在原链表上不停地做结点的删除。为了方便你理解,我制作了动图演示,如下所示:
【代码】基于以上思想,可以写出代码如下(解析在注释里):
class Solution {public ListNode removeElements(ListNode head, int val) {ListNode dummy = new ListNode();ListNode tail = dummy;ListNode p = head;while (p != null) {ListNode back = p.next;if (p.val != val) {tail.next = p;tail = p;}p = back;}tail.next = null;return dummy.next;}}
复杂度分析:时间复杂度 O(N),空间复杂度 O(1)。
【小结】我们将这道题的考点层层剥离之后,就只剩下生成 dummy 新链表,尾巴追加新结点,以及新链表的思路。关于解决这道这类题目的思路、重点以及分析方法,建议你先尝试自己梳理总结,再来看我给出的思维导图:
如果我们仔细对比链表反转与删除结点,会发现,这两者的不同之处在于:
- 链表反转使用的是头部插入的方法
- 删除结点采用的是尾部追加的方法
只是换了一个考点,题目就完全大变样了。如果我们再严格地对比这两个题目,可以发现:
- 链表反转时,头部插入是无条件的
- 删除结点时,尾部 append 是有条件的
这种条件的千变万化,会带来很多有趣的题目。比如下面这道练习题。
练习题 1:给定一个排序链表,删除重复出现的元素,使得每个元素只出现一次。
输入: 1->1->2->3->3
输出: 1->2->3
练习题 2:给定一个排序链表,删除重复出现的元素,只留下没有重复出现的元素。
输入:1->1->2->3->3
输出:2
你可以把答案或者思考的过程写在评论区,我们一起讨论。
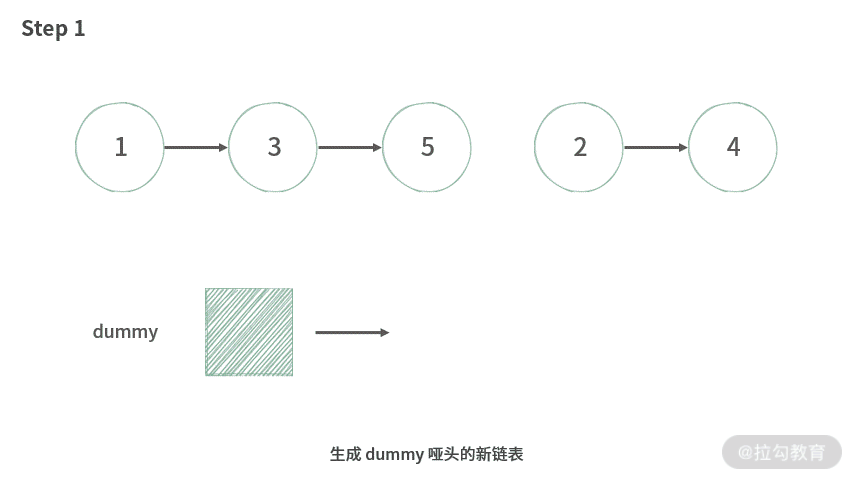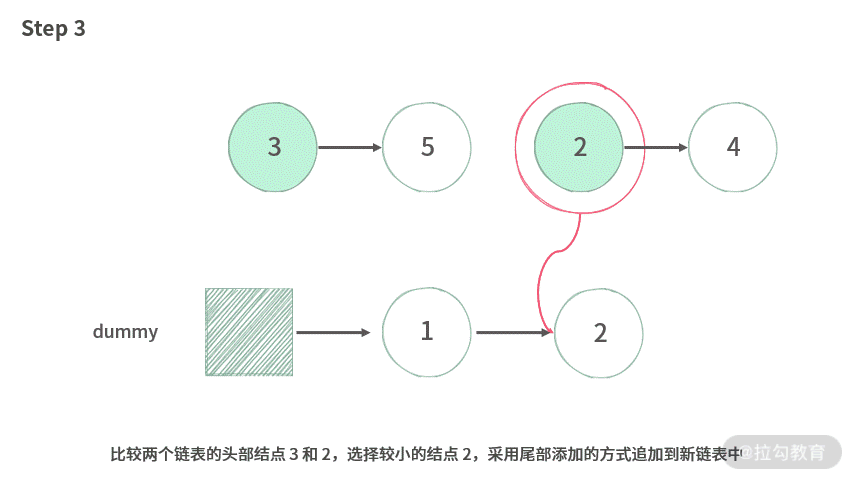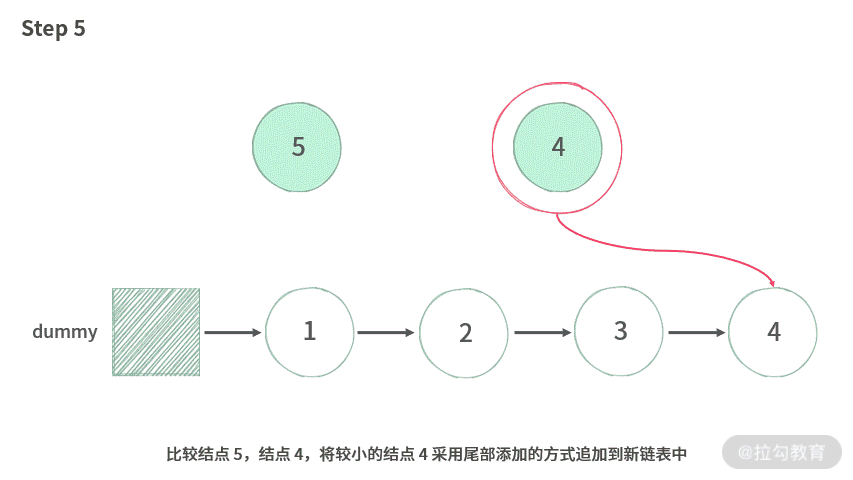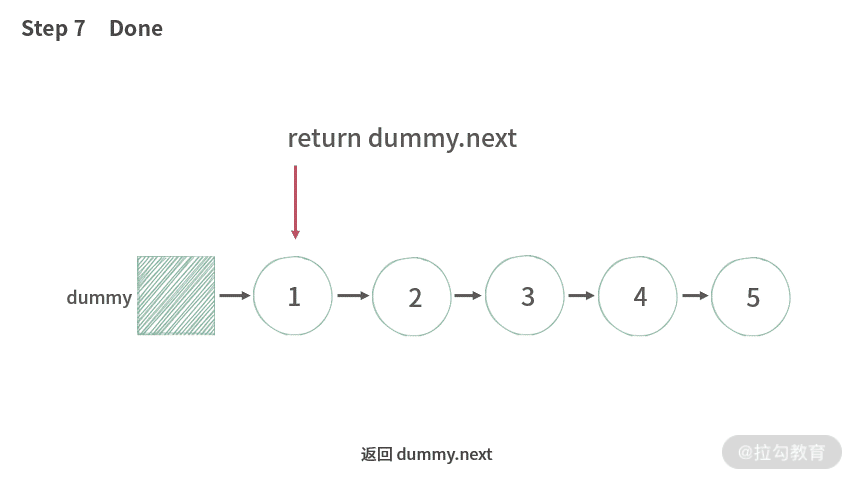
例 3 :合并
【题目】合并给定的两个有序链表。
输入:a = 1->4->6, b = 3->5->7
输出:1->3->4->5->6->7
【分析】首先应该是生成一个带假头的新链表 C,然后把 A,B 中的元素从小到大,依次添加到新生成的链表 C 中。因此,我们还需要使用到尾部插入法。
具体操作方法如下。
- 第一步:A,B 两个指针分别指向 A,B 链表的表头。
- 第二步:依次取出 A,B 两个指针中更小的值加入新链表中。
- 第三步:返回 C 链表假头的 next。
具体演示如下所示:
【代码】有了前面的思路,可以写出代码如下(解析在注释里):
class Solution {public ListNode mergeTwoLists(ListNode l1, ListNode l2) {ListNode dummy = new ListNode();ListNode tail = dummy;while (l1 != null || l2 != null) {if (l2 == null || l1 != null && l1.val < l2.val) {tail.next = l1;tail = l1;l1 = l1.next;} else {tail.next = l2;tail = l2;l2 = l2.next;}}tail.next = null;return dummy.next;}}
复杂度分析:时间复杂度 O(N),空间复杂度 O(1)。
【小结】如果我们再分析一下这道题目,可以发现考点仍然是:
- 生成 dummy 新链表
- 选择结点往新链表尾部追加数据
此时的尾部 append 是有条件的:需要从两个链表头中选择一个较小的数据进行追加。当然,有条件的 append 还可以变成各种其他的条件来操作。不过即使千变万化,只要你看清楚题的考点,就能轻松应对、。
那么这里我们不妨再选择其中一个考点 “选择较小的数” 进行练习。在原题中,只有两个链表,所以可以直接通过比较得到较小的结点。可是如果有 k 个链表要合并的时候,又应该怎么做呢?比如下面这道练习题:
练习题 3:给定 k 个有序链表,合并成一个有序链表
输入:[1->4->5,1->3->4, 2->6]
输出:[1->1->2->3->4->4->5->6]
你可以把答案或者思考的过程写在评论区,我们一起讨论。
例 4:交换链表中的结点
【题目】给定一个链表,需要将里面的结点两两交换。
输入:[1->2->3->4->5->6]
输出:[2->1->4->3->6->5]
【分析】经过观察发现,只不过把偶数位置与奇数位置的结点进行了交换。为了避免在原始链表中进行结点间的交换操作,我们可以采用如下方法:
- 生成两个新链表,一个用来存放奇数位置结点的链表 odd,一个用来存放偶数位置结点的链表 even;
- 遍历旧链表,并且把奇数位置上的结点放到 odd 链表中,把偶数位置的结点放到链表 even 中;
- 合并 odd 链表与 even 链表。
为了方便你理解,我同样制作了动图演示,如下:
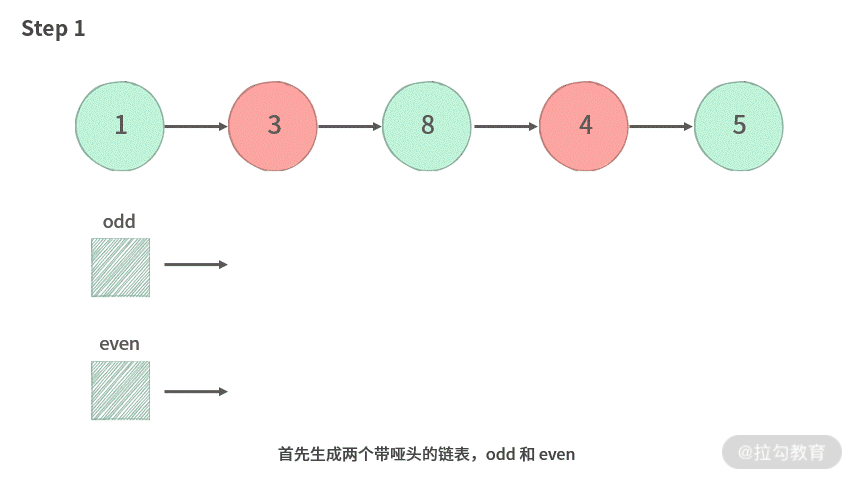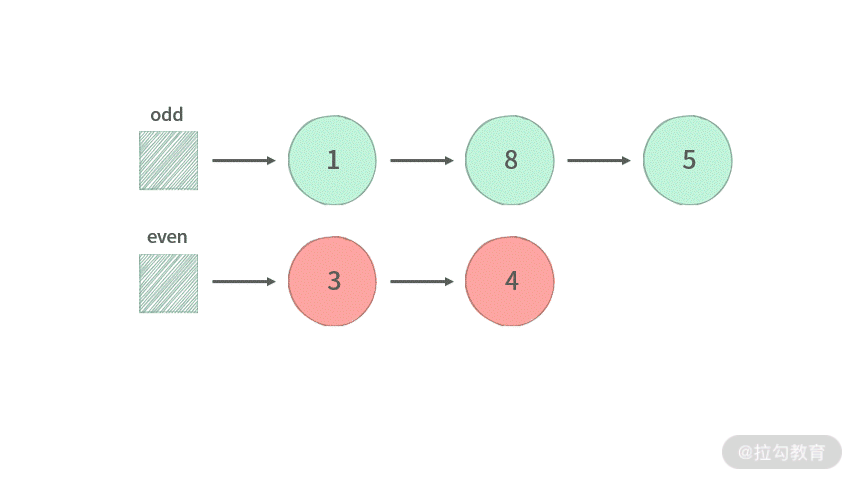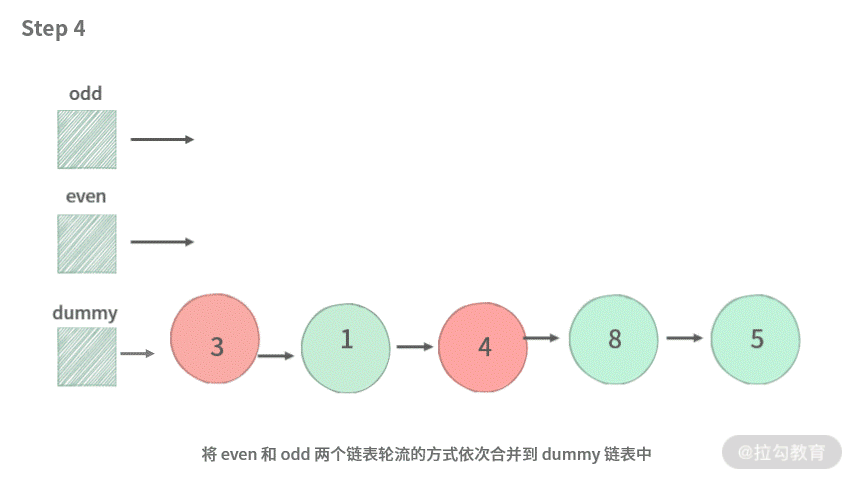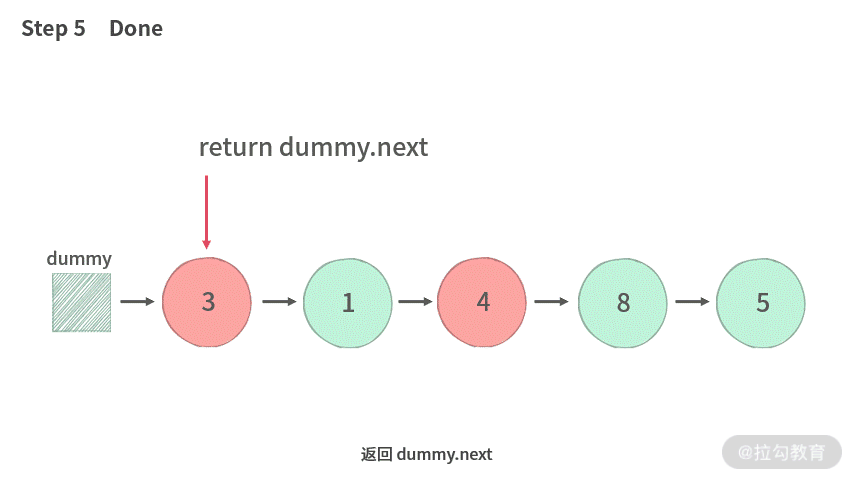
到这里,新增链表已经从一条变成了两条,来帮助我们解决这道题目。
【代码】有了思路,我们可以写出代码如下(解析在注释里):
class Solution {private ListNode mergeList(ListNode a, ListNode b) {ListNode dummy = new ListNode();ListNode tail = dummy;while (a != null || b != null) {if (a != null) {tail.next = a;tail = a;a = a.next;}if (b != null) {tail.next = b;tail = b;b = b.next;}}tail.next = null;return dummy.next;}public ListNode swapPairs(ListNode head) {ListNode oddDummy = new ListNode();ListNode oddTail = oddDummy;ListNode evenDummy = new ListNode();ListNode evenTail = evenDummy;int index = 0;ListNode p = head;while (p != null) {ListNode back = p.next;if ((index & 0x01) == 0) {evenTail.next = p;evenTail = p;} else {oddTail.next = p;oddTail = p;}index++;p = back;}oddTail.next = null;evenTail.next = null;return mergeList(oddDummy.next, evenDummy.next);}}
复杂度分析:每个结点会访问两次,拆分一次,合并一次,所以时间复杂度为 O(N),空间复杂度为 O(1)。
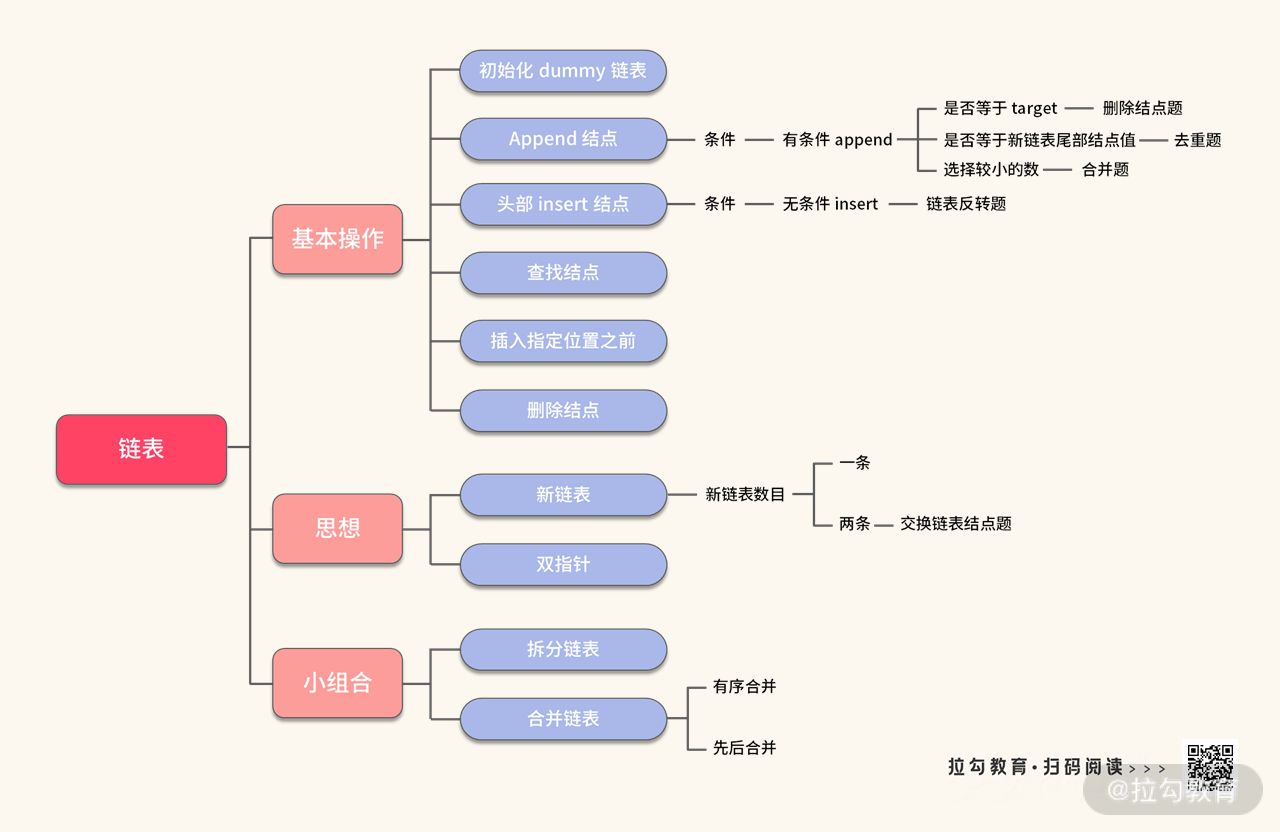
【小结】这道题的考点也比较明确了,可以拆分出以下考点:
- 拆分链表
- 新链表的思路
- 合并链表的操作
尤其需要注意的是,使用新链表思路时,可以通过生成多条新链表来解决以前处理起来比较麻烦的问题。至此,我们一起进一步扩展了链表知识。此外,还发现了一些小型的组合操作,比如:拆分链表,合并链表。在合并时,如果按照不同的条件合并,就需要写出不一样的合并代码,结合前面例 3,可以知道合并分两种:
- 有序合并
- 先后合并
到这里可以总结出我们更加丰富的知识路线图,如下图所示:
在这道题中,链表是两两成对进行了反转,那么如果是 k 个一组进行反转应该怎么办呢?我们再来看看与交换有关的练习题。
练习题 4:给定一个链表,要求将链表 k 个一组进行反转,如果最后一组不足 k 个,那么不反转。返回反转之后的链表。
输入:A = [1, 2, 3, 4, 5], k = 2
输出: [2, 1, 4, 3, 5]
练习题 5:给定一个链表,从链表尾部开始,k 个一组进行反转,如果左边的分组不足 k 个,那么不反转。返回反转之后的链表。
输入:A = [1, 2, 3, 4, 5], k = 2
输出:[1, 3, 2, 5, 4]
解释:注意是从链表的尾部开始 k 个一组的。所以这里是[1], [2, 3], [4, 5]这样分组来进行反转。
三板斧的第三斧:双指针
虽然新链表的思路非常有趣,但是关于它的更多探索还是应该留给你自己。收拾好行囊,我们将要去看更加瑰丽的奇景——双指针。
双指针,顾名思义就是两个指针在链表上移动。实际上,我们在前面链表的查找中已经使用过双指针了:比如链表中指定位置插入一个新结点,就使用了两个指针,一前一后两个指针在链表上前进。
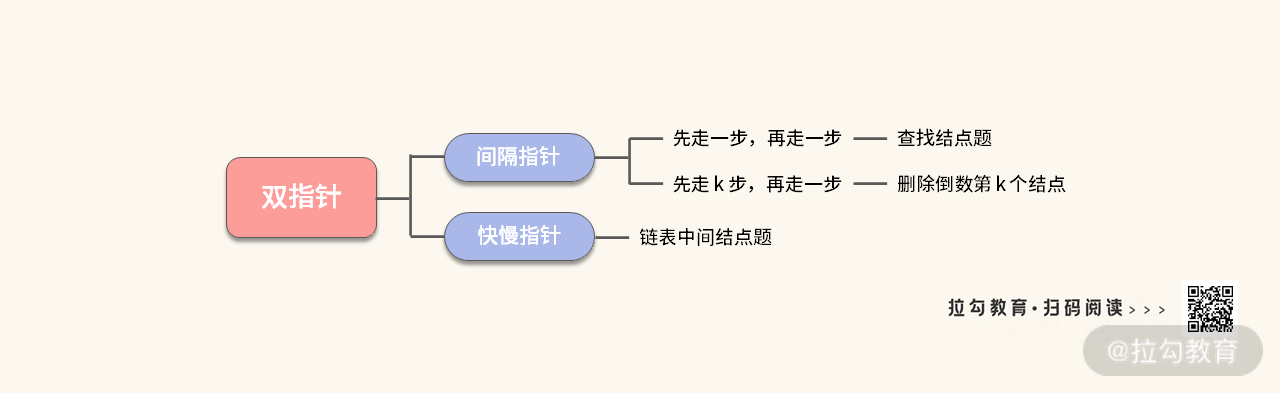
其实两个指针在链表上前进时,有很多种形式,常见的主要有以下两种。
- 间隔指针:前面的指针先走一步,然后后面的指针再一起走;前面的指针先走 k 步,后面的指针再一起走。
- 快慢指针:两个指针的速度一快一慢前进,比如一个每次走一步,一个每次走两步。
接下来,我们来看看双指针能解决什么类型的问题。
例 5:链表的倒数第 k 个结点
【题目】给定一个链表,删除链表中的倒数第 k 个结点。这里我们认为最后一个结点是倒数第 1 个。
输入:1->2->3, k = 2
输出: 1->3
【分析】首先第一种常规思路是,先统计出整个链表的长度 len, 再去取第 len-k 结点的前驱进行删除。
但是,面试的时候,面试官往往会加一个限制条件 :只能遍历链表一次。
以后凡是遇到链表题,看到这句话,实际上就是在告诉你 “用双指针吧”。思路如下:
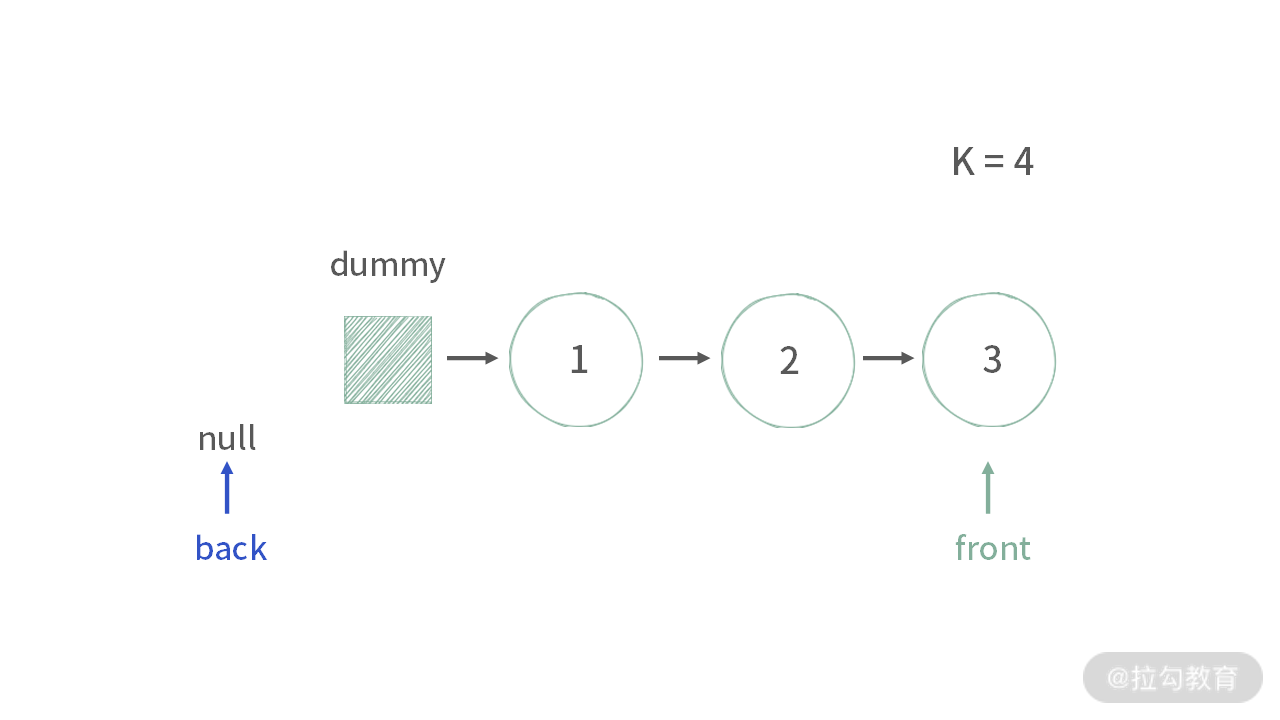
- 在原链表前面加上 dummy,变成带假头的链表
- front 指针从 dummy 开始,走 k 步,然后停下来
- back 指针指向链表 dummy 假头
- 然后两个指针再一起走
- 当 front 指针指向最后一个结点时,back 指针刚好指向倒数第 k 个结点的前驱。
解题思路有了,还有两个细节需要你特别注意。
【细节 1】你需要小心处理三种情况:
- 链表长度 < k,此时什么也不做;
- 链表长度 == k,此时删除原来的链表头结点;
- 链表长度 > k,此时找到倒数第 k 个结点的前驱,然后删除倒数第 k 个结点。
接下来,我们分别讨论这三种情况。
情况 1:链表长度小于 k。front 指针会先走 k 步,如果链表长度小于 k,那么必然会导致 front 指针行走的步数小于 k,此时应该什么也不做。
情况 2:链表长度等于 k。此时需要删除倒数第 k 个结点,也就是旧链表的 head 结点。
当 front 指针先走完 k 步之后,back 指针刚好位于 dummy 结点。而 dummy 结点就是倒数第 k+1 个结点,那么此时可以直接通过 back 指针删除它后面的结点(刚好是 head,也就是倒数第 k 个)。
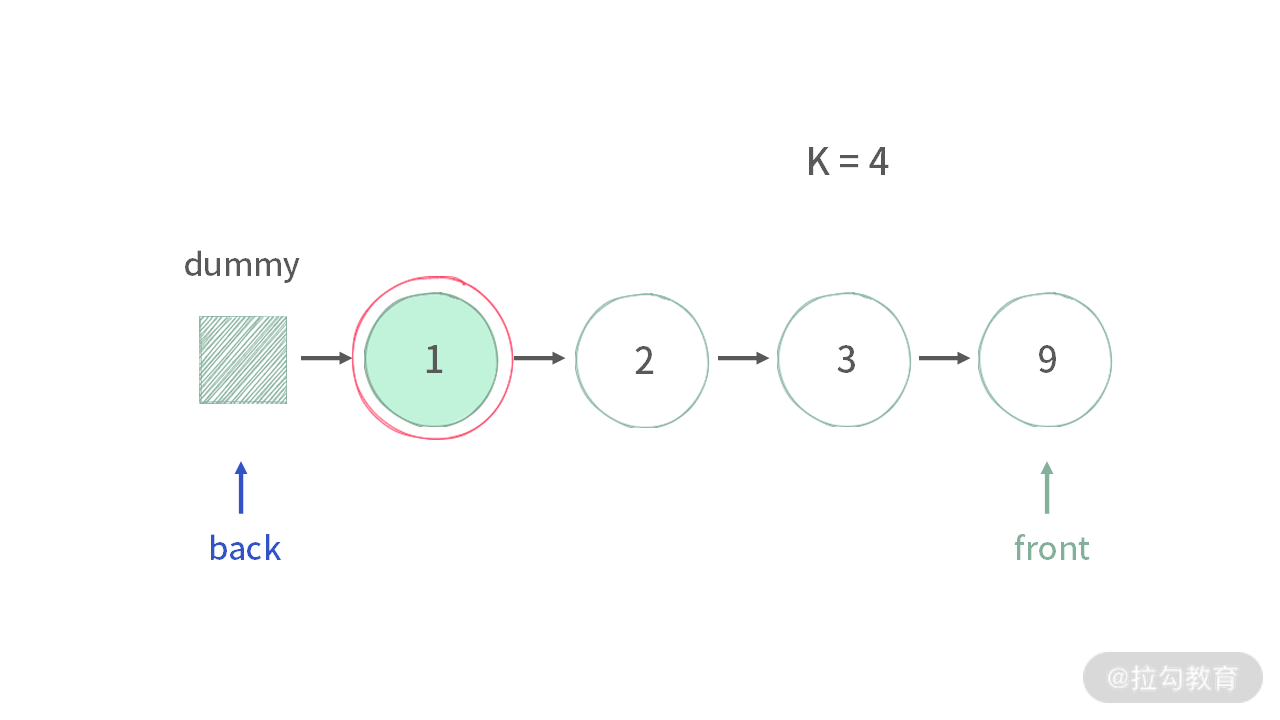
情况 3:链表长度大于 k。back 指针刚好位于倒数第 k+1 个结点,此时可以直接通过 back 指针删除它后面的结点(刚好是倒数第 k 个)。
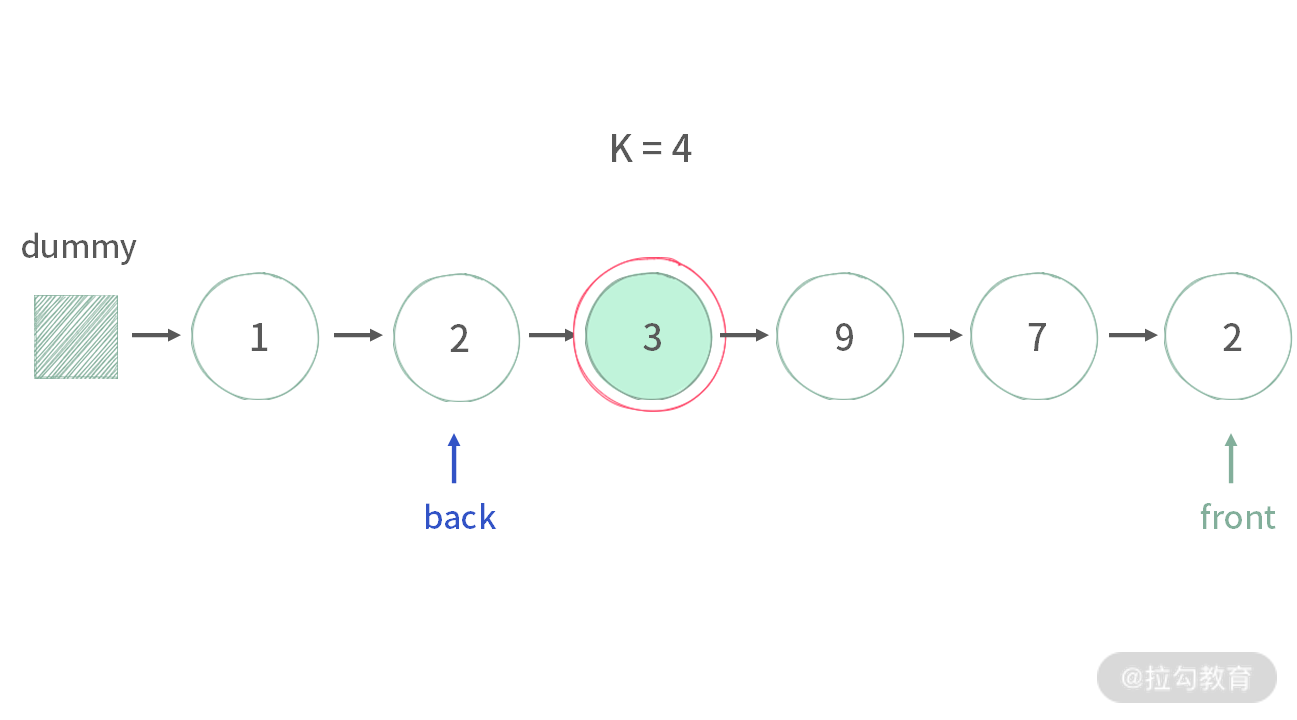
我们发现:情况 2 和情况 3 实际上都是用 back 指针来删除后面的结点。因此,这两种情况可以一起处理。
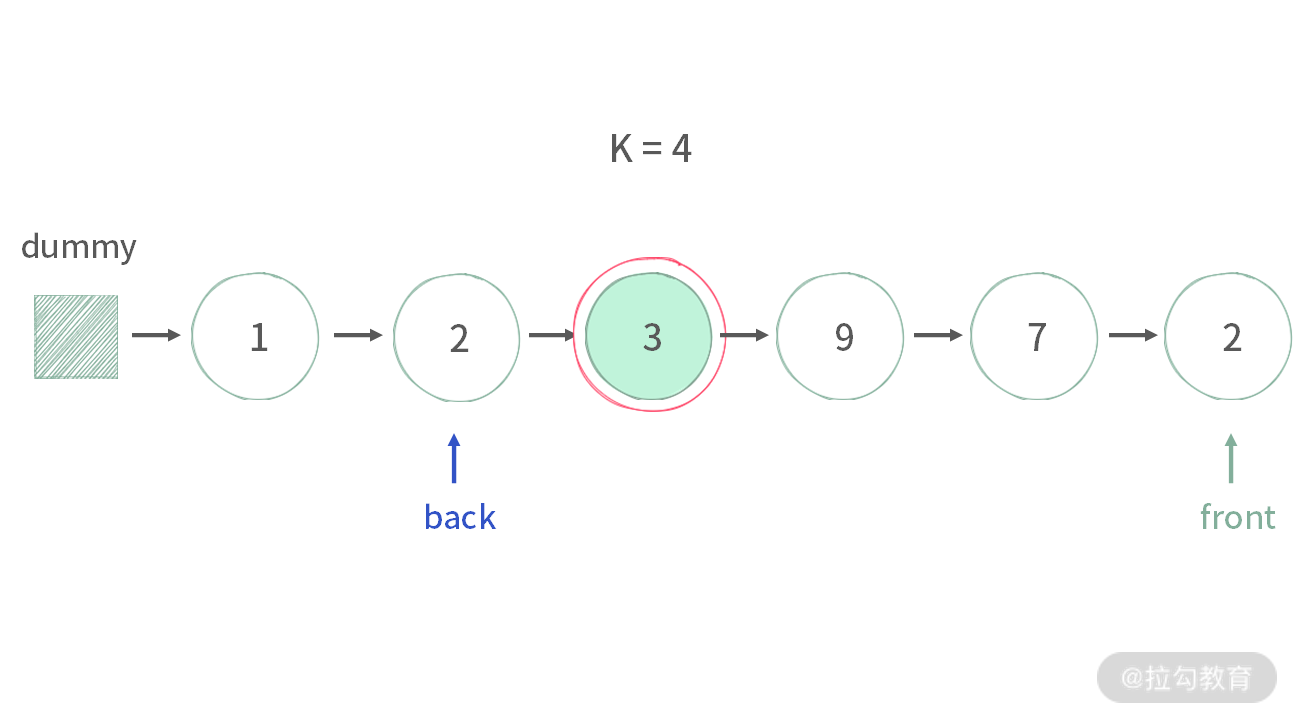
【细节 2】任何时候,front 最后停下来的位置一定要位于链表的最后一个结点。这是因为:要想删除倒数第 k 个结点的前驱结点,需要 back 刚好指向倒数第 k+1 个结点,那么就必须要让 front 非空,即指向倒数第一个结点。
【代码】有了思路以及相应的细节,我们就可以利用代码来解决问题了(解析在注释里):
class Solution {public ListNode removeNthFromEnd(ListNode head, int k) {ListNode dummy = new ListNode();dummy.next = head;int preWalkedSteps = 0;ListNode front = dummy;while (preWalkedSteps < k &&front != null && front.next != null) {front = front.next;preWalkedSteps++;}ListNode back = dummy;while (front != null && front.next != null) {back = back.next;front = front.next;}if (preWalkedSteps == k) {back.next = back.next.next;}return dummy.next;}}
复杂度分析:时间复杂度 O(N),空间复杂度 O(1)
【小结】当做完这道题之后,我们可以进一步完善双指针的技巧,总结的思维导图如下:
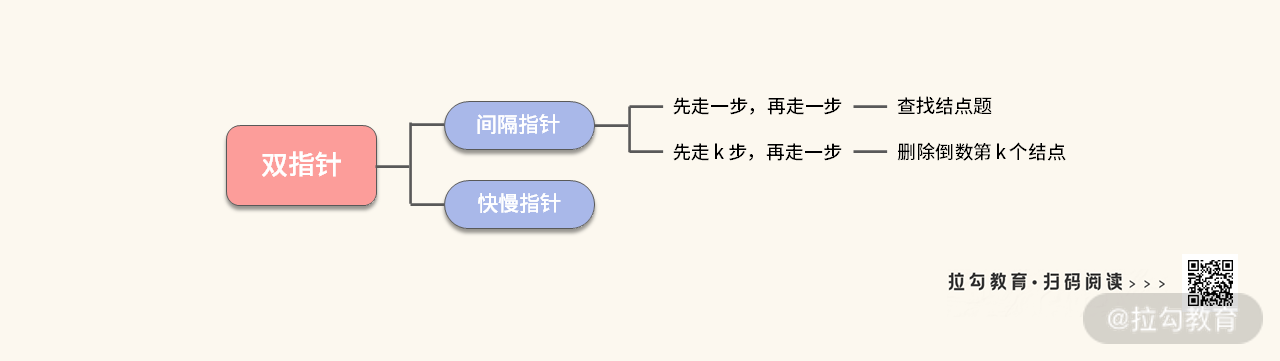
然后,我们再来总结一下这道题目的考点。首先除了思路 “双指针” 以外,你还需要注意写代码的技巧。
- 将旧链表改造成带 dummy 结点的链表,方便删除 head 结点。这是能让情况 2 和情况 3 统一处理的关键。
- 让指针指向链表最后一个结点的 while 语句的写法。
- 利用移动步数来判断链表长度与 k 的关系。
接下来我们一起看一下双指针的另外一种形式,快慢指针。
例 6:拆分链表
【题目】给定一个链表,需要把链表从中间拆分成长度相等的两半(如果链表长度为奇数,那么拆分之后,前半部分长度更长一点)。
输入:[1->2->3->4->5]
输出:[1->2->3, 4->5]
【分析】我们需要分为 2 步:
- 找到链表的中间结点
- 从中间结点把链表分为两半
那么问题是,如何找到中间结点呢?如果是首先求出链表的长度,然后再利用 getPreNode(len/2) 函数的前驱,再把链表拆分成两半。
但是,这可能不是面试官想要的解法,因为这种解法会将链表遍历两遍,面试官可能会说:“只能遍历一次”。又听到了这个声音,这就是告诉你需要用双指针了。
所以问题的关键就是如何使用双指针找到链表的中间结点,可以采用如下办法:
- 假设链表头在左边,尾巴在右边,两个指针 s1、s2 从链表头开始往右走;
- s1 表示每次只往前走一步,s2 则表示每次只往前走 2 步;
- 在同样的时间内,当 s2 指向链表的末尾,s1 指针便指向链表的中间结点。
只是在写代码的时候,需要特别注意以下 2 点:
- 当有偶数个结点,s2 是空指针,此时,s1 位于后半部分指针的头部,因此需要返回s1 的前驱;
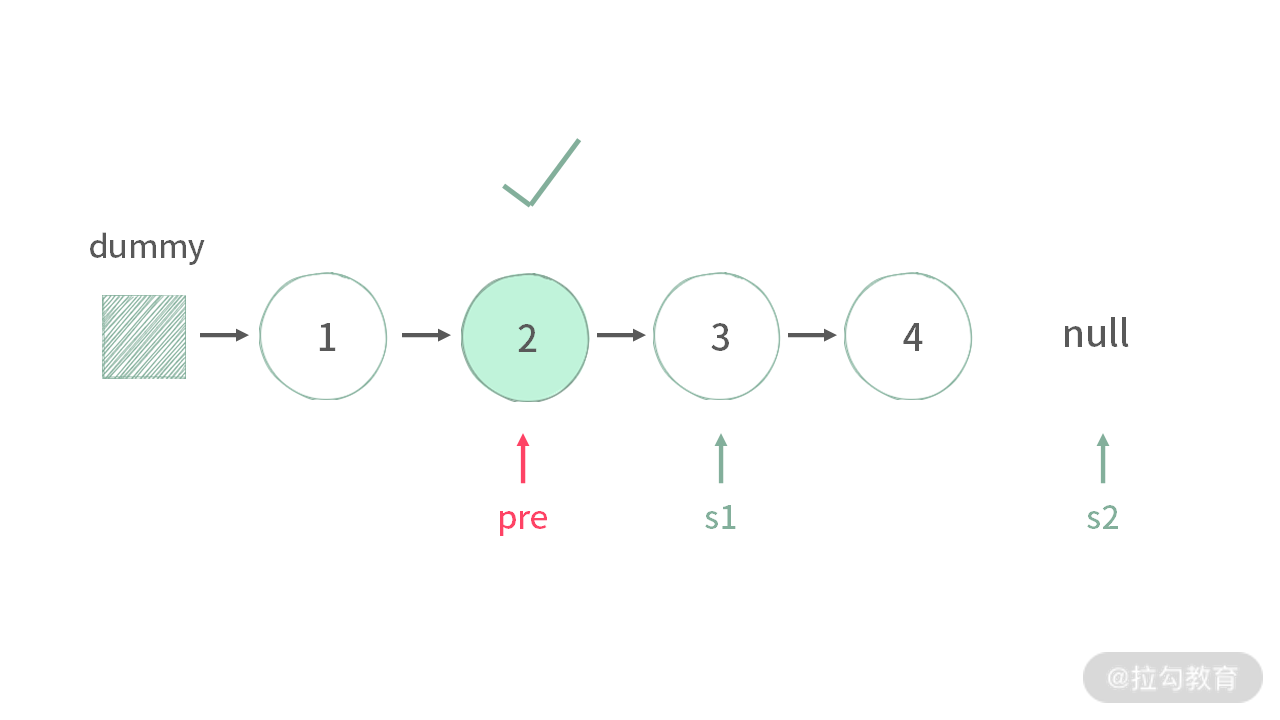
- 当有奇数个结点,s2 是最后一个结点,此时 s1 指针位于前半部分的最后,直接返回 s1即可。
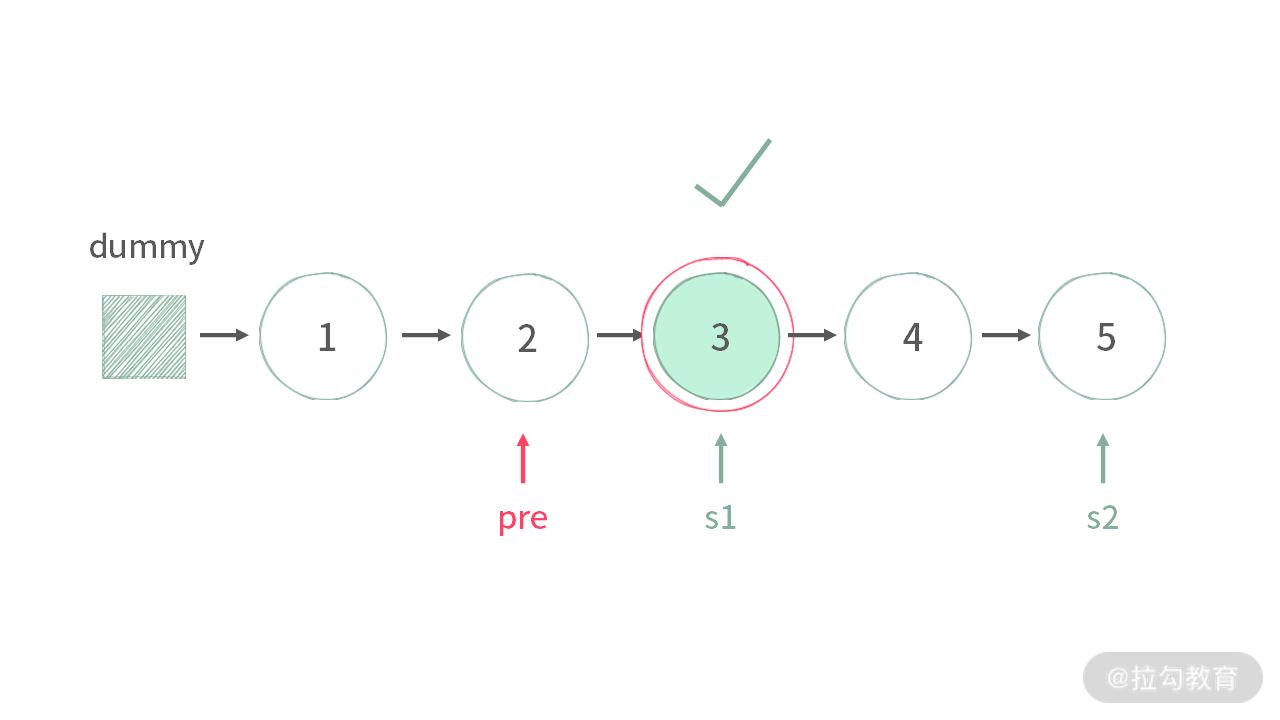
如果找到了中间结点,那么就可以直接进行拆分了。
【代码】接下来我们就实现拆分链表的逻辑,代码如下(解析在注释里):
class Solution {private ListNode findMiddleNode(ListNode head) {ListNode dummy = new ListNode();dummy.next = head;ListNode s2 = head;ListNode s1 = head;ListNode pre = dummy;while (s2 != null && s2.next != null) {pre = s1;s1 = s1.next;s2 = s2.next.next;}return s2 != null ? s1 : pre;}public ListNode[] split(ListNode head) {ListNode mid = findMiddleNode(head);ListNode back = mid.next;mid.next = null;return new ListNode[]{head, back};}}
复杂度分析:时间复杂度 O(N),空间复杂度 O(1)。
【小结】这道题的核心就是如何通过双指针找到链表的中间结点。考点还是清晰明了,我们可以再将双指针的分析要点总结如下:
不过对于这道题,我想给你留几个有趣的小问题,可以帮助你加深代码的理解,希望你可以尝试回答以下两个问题,并写在留言区,我们一起讨论。
- 为什么没有判断空链表,对于空链表的支持是怎么完成的?
- 为什么 s1, s2 要从 head 开始走,如果从 dummy 开始走可以吗?如果可以,会有什么样的代码改动?
练习题 6: 将一个链表进行重排,如果我们用 L[x] 表示链表的第 x 个结点(从 0 开始)。将链表 L[0]->L[1]->L[2]->L[3]-> …. ->L[N-1] 重新排列为 L[0]->L[N-1]->L[1]->L[N-2]->L[2]->L[N-3]…..。
输入:1->2->3->4->5
输出:1->5->2->4->3
例 7:链表环问题
【题目】给定一个链表,原本的链表尾巴如果不为空,并且指向了链表的中间结点,这样我们就认为这个链表存在一个环。给定一个链表,判断链表中是否存在环?
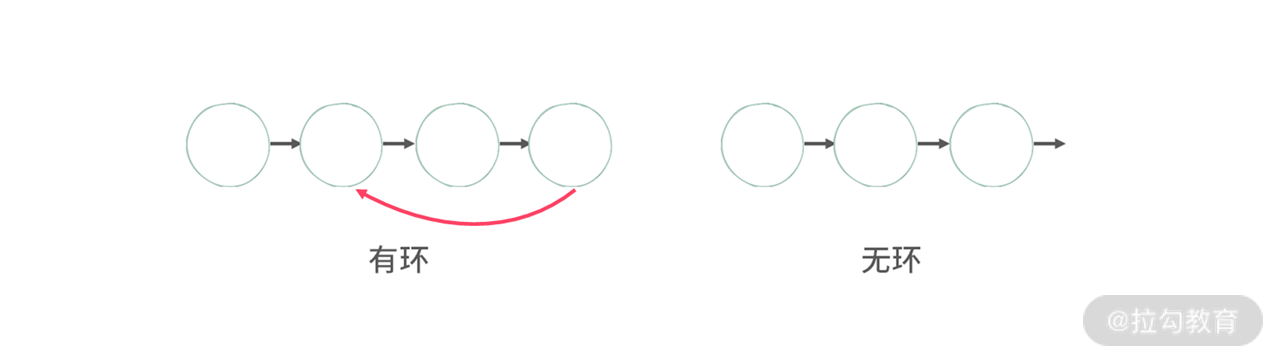
【分析】首先,如果链表中存在环,只用一个指针遍历肯定是永无止境的,这一个指针会在环里面打转。因此,我们可以再次利用双指针,s1,s2 两个指针都从链表头开始,s1 指针表示每次只往前走一步,s2 指针则是每次只往前走两步。那么链表最终只有两种情况:
1.s1 == s2,这个时候链表存在环;
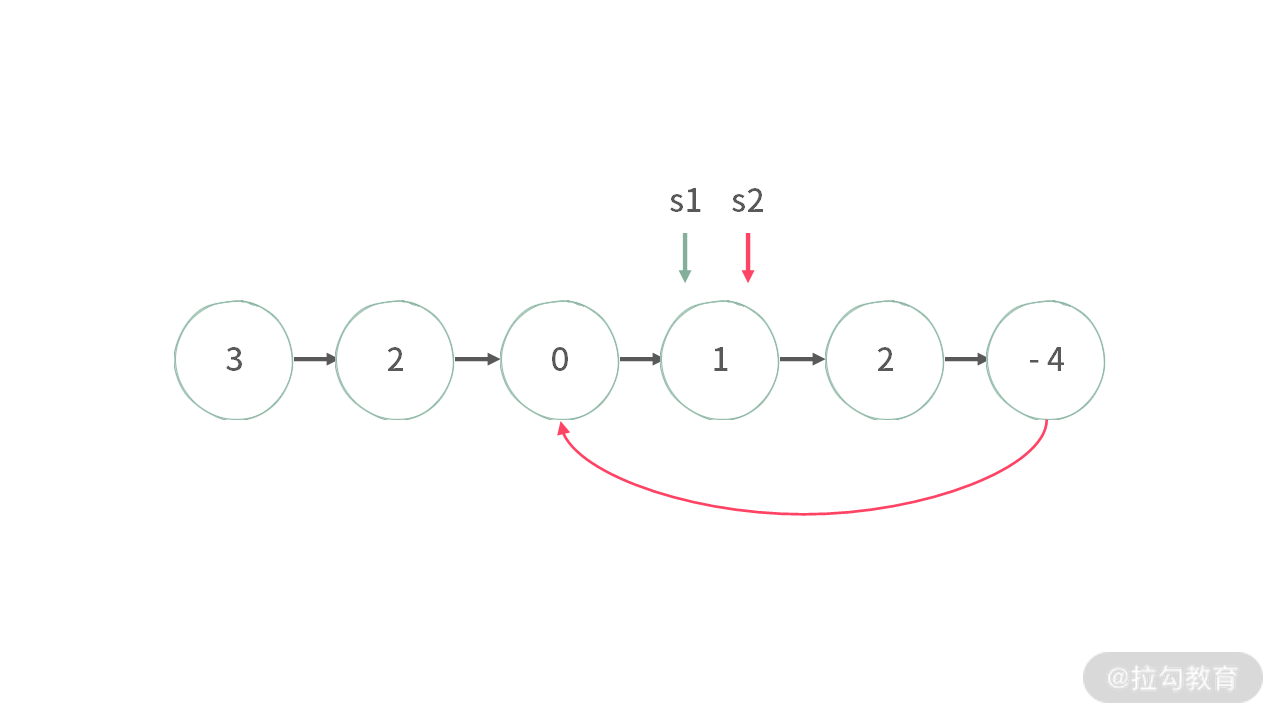
2.s1 != s2,这个时候链表不存在环。
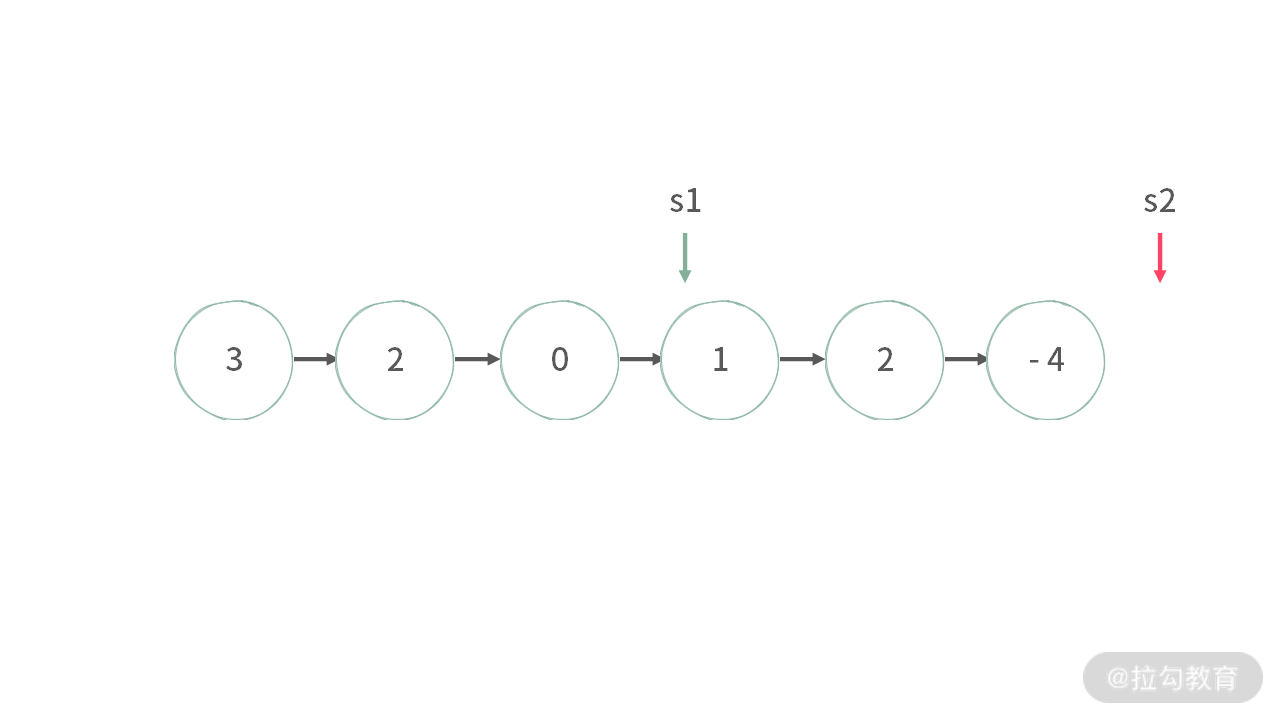
不过我们还是需要处理两种边界条件:
- 当为空链表的时候,s1 == s2,但是实际上此时链表无环;
- 当链表中只存在一个结点,并且无环的时候,运行的结果也会是 s1 == s2。
这两种边界条件的处理,只需要特殊判断一下即可。
【代码】有了前面了思路,那么我们就可以写出解问题的代码了(解析在注释里):
public class Solution {public boolean hasCycle(ListNode head) {if (head == null || head.next == null) {return false;}ListNode s1 = head;ListNode s2 = head;while (s2 != null && s2.next != null) {s2 = s2.next.next;s1 = s1.next;if (s1 == s2) {break;}}return s1 == s2;}}
复杂度分析:时间复杂度为 O(N),空间复杂度为 O(1)。
【小结】至此,我们完成了快慢指针的学习,可以在知识图谱中加上链表环问题了,如下图所示:
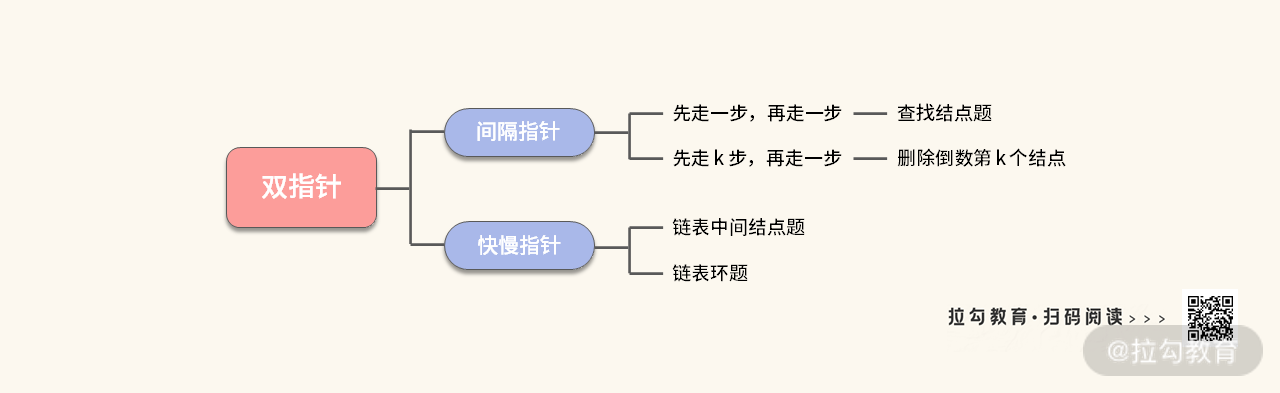
这里我还想给你留一个小问题:在寻找链表环的过程中,对于两种特殊情况,我们实际上进行了特殊判断,那么有没有什么办法可以避免这种特殊的断呢?
小提示:想想我们之前学习过的假头。
老规矩,希望你尝试思考并把想法写在留言区,期待和你一起讨论。另外,我也会根据大家的留言反馈,不定时输出加餐内容,比如练习题详解、留言区问题点评等。
【扩展】在面试中,伴随着链表环问题的,往往还有后招:如果链表中存在环,能不能把形成环的那个结点找出来?
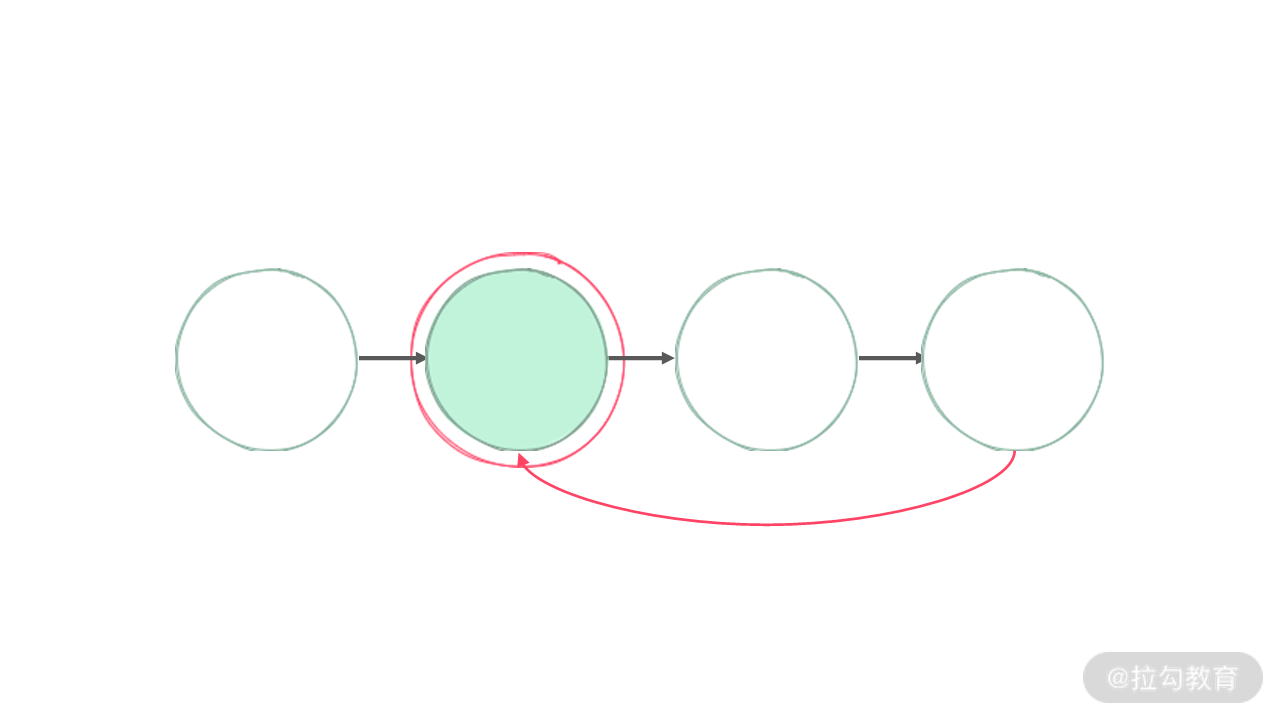
我们可以把这个问题转化成一个数学问题。我们一起看一下下面这张图:
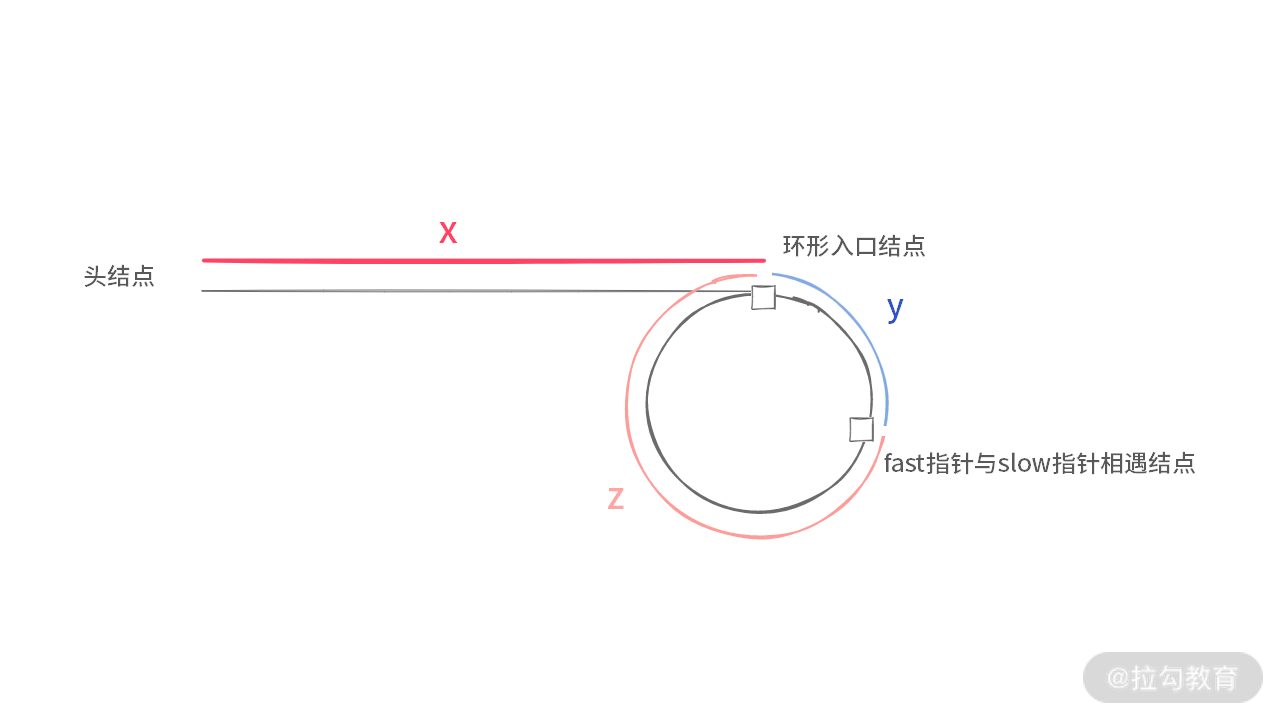
这里我们只考虑链表存在环的情况。假设 s1 慢指针与 s2 快指针在环中某个位置相遇。此时:
- s1 指针走过的路径长度为 a = x + y
- s2 指针走过的路径长度为 b = x + y + n * (y + z)
由于两个指针都是从同一个地点出发,s2 指针走得更快,那么走的长度肯定是 s1 指针的两倍。所以可以得到 b = 2a,即 b = x + y + n * (y + z) = 2x + 2y
由此,可以推导出 x = n (y + z) - y = (n-1)(y+z) + z,即 x - z = (n-1) * (y + z)
从 x-z 表达式可以看出,如果有两个指针同时从头结点,相遇结点这两个地方出发,它们肯定会在环形入口相遇。因为它们之间的差值刚好是圆环长度的整数倍(更加严格一点的证明可以用数学归纳法)。
经过数学证明,我们可以写出求解代码如下(解析在注释里):
public class Solution {public ListNode detectCycle(ListNode head) {if (head == null || head.next == null) {return null;}ListNode s1 = head;ListNode s2 = head;while (s2 != null && s2.next != null) {s1 = s1.next;s2 = s2.next.next;if (s1 == s2) {break;}}if (s1 != s2) {return null;}s1 = head;while (s1 != s2) {s1 = s1.next;s2 = s2.next;}return s1;}}
复杂度分析:时间复杂度为 O(N),空间复杂度为 O(1)。
总结与延伸
经过这两讲的学习,你终于可以用这三板斧来毒打链表题了,在抄家伙之前,我们一起回想下每招式的作用吧。
- 第一斧:假头。假头的作用主要是避免关于空链表的判断与讨论,假头还可以用来避免检查前驱结点为空的情况。
- 第二斧:新链表。新链表的引入是为了解决在旧链表中进行原地的交换、插入、删除,把复杂的操作变成在新链表中头部插入或者尾部添加。
- 第三斧:双指针。双指针主要是用于寻找链表中的特定结点,双指针的走法可以一次一步,可以有快有慢,出发点也可以有前有后。
了解了思路,你还需要深入理解操作的代码模板,然后就可以成功地进行解题实战了。这里我已经为你总结好了《链表题通关路线图》,请参照此地图来通关链表题吧。
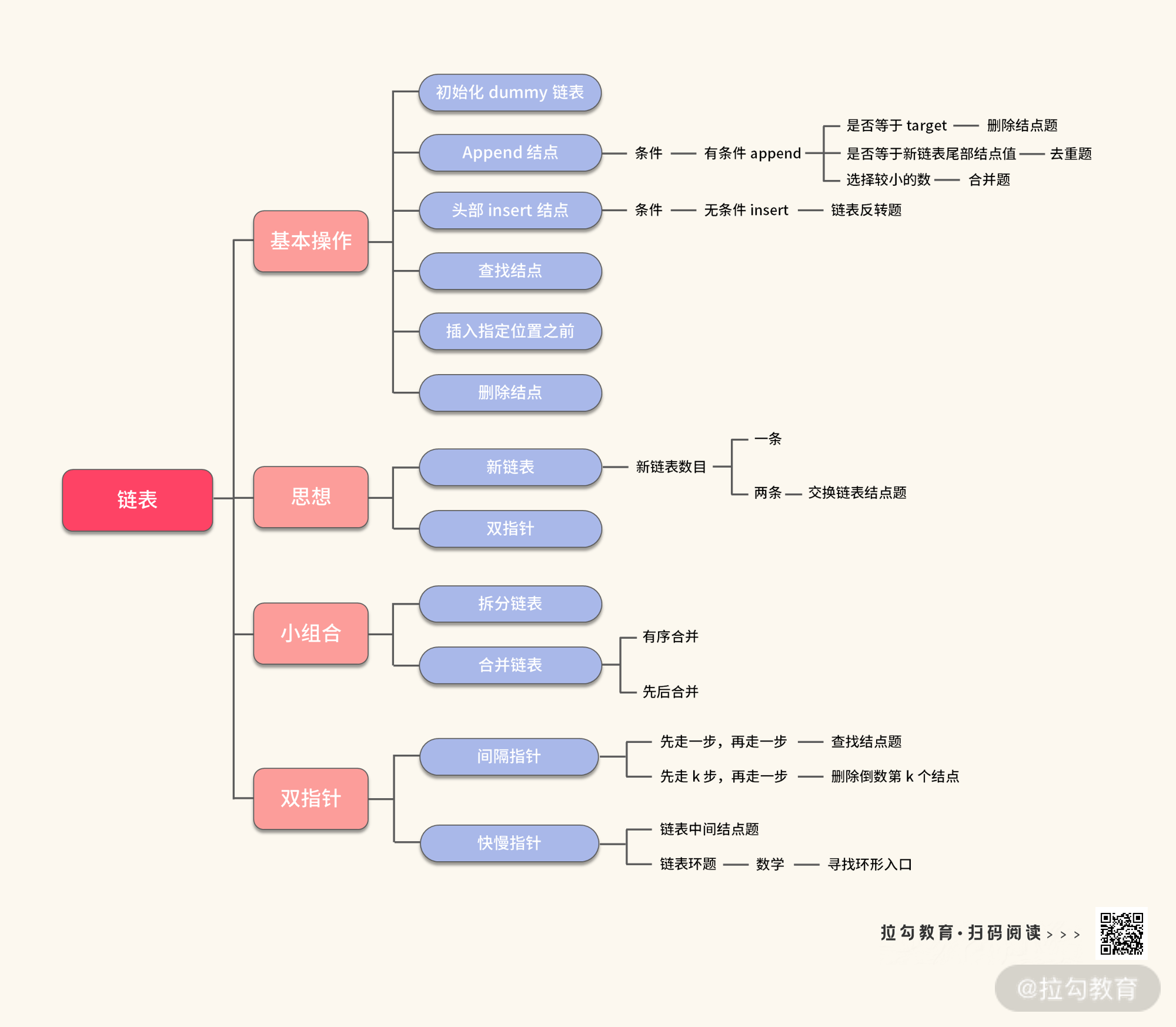
链表操作是很多其他复杂算法的基础,需要你熟练掌握,比如 LRU,跳表等数据结构里面都会用到链表。希望你课后能熟练地运行本讲介绍的思路。
此外,从算法的难度上来说,实际上链表题并不算太难,但是非常考验基本功。我在处理链表题时,经常把文中介绍的题目作为模板深刻理解,达到熟练记忆的程度。我希望你在理解解题思路的基础上,也能够熟练记忆这些模板,逐渐建立一个系统的知识体系。
思考题
最后,我再给你留一道思考题。
链表排序:给定一个单向链表,如何给这个链表排序,要求复杂度达到 O(nlogn)。
- 你能使用所讲的创建新链表 + 快排的思想吗?
- 你能使用快慢指针 + 合并排序的思想来解决吗?
学会了链表的三板斧,处理链表问题,变得越来越容易了。不过我们可不能总是待在舒适区,还有很多算法与数结构等着我们去征服。下一讲将介绍 06 | 树:如何深度运用树的遍历?记得按时来探险。

