算法是为了解决某个问题抽象而成的计算方法,我们可以简单地把算法比作一个拥有输入和输出的函数,这个函数总能在有限的时间经过有限的步骤给出特定的解。
以往的前端开发场景中使用到算法的情况并不多,原因有下面 3 个。
- 前端开发场景更关注页面效果及用户交互,大多数开发的时候只需要按照自然逻辑来编写代码即可,比如响应用户事件、控制组件加载与页面跳转,对于数据的操作停留在校验、请求、提交及格式化这些基础的操作,涉及数据计算的场景比较少。
- 前端运行环境浏览器性能有限,如果把大量的数据放到前端进行计算,无论是网络加载还是渲染数据都将耗费大量时间,从而导致用户体验下降。
- 在多端的系统中,算法运用在后端会更加高效。如果将算法运用在前端,很可能意味着需要在不同环境用不同语言重新再实现一遍。举个简单而不是特别恰当的例子,假设需要给用户展现一个树形图表,如果后端直接返回关系数据库中查询到的表结构数据,那么前端则需要先将其转换成树结构的 JSON 数据才能填充到对应的组件,那么在 iOS 和 Android 设备上也要执行同样的逻辑,但是由于语言不同,这些代码逻辑无法复用,都必须单独编写;相反,如果后端拿到数据之后转化后再返回则能同时免去这些代码的编写。
但随着 Web 技术的不断发展,前端运行环境以及 Node.js 的计算能力不断加强,算法将被用于更多的开发场景中,对于前端工程师来说也将变得越来越重要。所以这一课时我们就来聊聊算法相关的内容。
算法性能指标
在衡量算法优劣的时候通常会用到两个重要的性能指标:时间复杂度和空间复杂度,分别用来表述算法运行所需要的运行时间和存储空间。
这里的 “复杂度” 我们可以理解为一个带有参数的函数,简写为 O,O 的参数一般为 1 或 n 的表达式。下面分别举例进行说明。
假设现在需要对一个首项为 1、差值为 1 的等差数列数组 arr 进行求和。如果像下面的代码一样采用 reduce 操作,则意味着需要遍历数组 arr 之后才能得到计算结果;如果数组 arr 的长度为 n,那么对应的累加操作 acc+=cur 这个表达式将被执行 n 次,因此这个操作的时间复杂度为 O(n)。
arr.reduce((acc, cur) => acc+=cur, 0)
对等差数列比较了解的同学应该知道,可以使用求和公式来计算结果,这样的话并不需要遍历数组,只需要把首项 arr[0]、项数 n 和公差 1 带入公式进行计算即可。
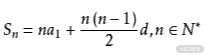
等差数列求和公式
整个操作只执行了一次,所以时间复杂度为 O(1),要优于 O(n)。也就是说,时间复杂度取决于表达式执行次数。
空间复杂度的计算思路和时间复杂度相似,但不是根据执行次数而是根据变量占用空间大小。下面通过一个例子进行说明。
假设现在要将数组 arr 中的元素向前移动一位,第一个元素移动到最后一位。如果直接在原数组上进行操作,只借助一个额外的变量实现,那么空间复杂度为 O(1)。
let tmp = arr[0]for(let i=0;i<arr.length - 1;i++) {arr[i] = arr[i+1]}arr[arr.length - 1] = tmp
如果将结果保存在一个新的数组中,那么空间复杂度为 O(n)。
let newArr = []for(let i=0;i<arr.length - 1;i++) {newArr[i] = arr[i+1]}newArr.push(arr[0])
为了方便比较复杂度,复杂度的计算还遵循下面两个简写原则:
- 多项式组成的复杂度,取最高次项,并省略系数,比如 O(3n+1) 简写成 O(n);
- 不同参数可以统一用 n 表示,比如遍历长度为 m 乘以 n 的数组,复杂度 O(mn) 写成 O(n^2)。
基于此,我们在优化算法时,如果只能优化系数或非最高次项操作,那么在算法复杂度计算来看,这种提升意义是比较小的。
常用的复杂度从优到劣排序,依次如下:
O(1)>O(logn)>O(n)>O(nlogn)>O(n^2)>O(x^n)
通常,如果不对复杂度进行特别说明,一般用时间复杂度指代算法复杂度。
TimSort 排序
排序算法就是让线性结构的数据按照升序或降序的方式排列的操作,是最基础也是使用频率较高的算法。排序的意义在于可以大大减少后续操作的时间复杂度。例如,在一个数组中找到第 2 小的数,对于无序数组需要对数组进行遍历,那么时间复杂度为 O(n),而在有序数组中可以直接通过下标获取,时间复杂度为 O(1)。
正因如此,对于排序这个基础的操作有多种算法,对具体的算法感兴趣的同学可以看一些对比分析文章,比如《十大经典排序算法(动图演示)》,里面分析对比了主流排序算法的(平均、最优、最坏)时间复杂度、空间复杂度、稳定度。
在前端领域,排序属于日用而不知的算法,因为 JavaScript 引擎早已把高效的排序算法写入数组的原型函数 sort 中了,这种高效的排序算法就是 TimSort。
TimSort 是一种在 Java、Python 等多种语言环境广泛应用的排序算法,是根据作者姓名 Tim Peters 而命名的。它是一种典型的混合算法,同时采用了折半插入排序和归并排序。最好的情况下,时间复杂度可以达到 O(n),最坏的情况下也能达到 O(nlogn),空间复杂度在最好情况和最坏情况下分别为 O(1) 和 O(n)。
TimSort 并不是简单地把两种排序方式进行组合,而是进行了一些优化。下面通过一个实例来了解它的具体实现步骤。
假设要对一个整数数组进行 TimSort 排序,那么具体的操作步骤如下所示。
首先,根据数组长度进行计算,得到一个数值 minRunLength,表示最小的子数组 run 的长度。minRunLength 的计算方式比较简单,对于长度小于 64 的数组直接返回数组长度,长度大于或等于 64 则不断除以 2 直到小于 64。 这个值的主要作用是用来控制 run 的数量,方便后续进行归并排序,避免一个超长 run 和一个超短 run 合并。
其次,通过 while 循环遍历数组,计算下一个 run 的长度,具体计算方式其实是根据索引值来遍历数组的,从第一个元素开始找寻最长的有序子数组,如果和排序方式不一致(比如在升序排序中找到一个降序子数组),那么就进行反转,然后返回这个有序子数组的长度,赋值给变量 currentRunLength。
再次,判断 currentRunLength 和 minRunLength 的大小,如果 currentRunLength 小于 minRunLength,那么通过折半插入排序合并成一个更长的 run。
另外,将得到的 run 压入栈 pendingRuns 中,等待进一步的合并。
进而,将 pendingRuns 中的部分 run 进行合并,使栈内的所有 run 都满足条件 pendingRuns[i].length > pendingRuns[i+1].length + pendingRuns[i+2].length && pendingRuns[i].length > pendingRuns[i+1].length。
最后,按次序合并 pendingRuns 中的 run,得到最终结果。
若对 JavaScript 中的 TimSort 实现仍有疑惑的话,建议查看具体源码,源码虽为 tq 文件,但语法风格和 JavaScript 差异不大。
补充 1:折半插入排序
折半插入排序(Binary Insertion Sort)是对插入排序算法的一种优化,插入排序算法就是不断地将元素插入前面已排好序的数组中,它的时间复杂度和空间复杂度分别为 O(n^2) 和 O(1)。折半插入就是用折半查找插入点取代按顺序依次寻找插入点,从而加快寻找插入点的速度。
下面是一段通过折半插入排序来对数组进行升序排列的示例代码:
function binayInsertionSort(arr) {for (var i = 1; i < arr.length; i++) {if (arr[i] >= arr[i - 1]) continuelet temp = arr[i];let low = 0;let high = i - 1;while (low <= high) {mid = Math.floor((low + high) / 2);if (temp > arr[mid]) {low = mid + 1;} else {high = mid - 1;}}for (var j = i; j > low; --j) {arr[j] = arr[j - 1];}arr[j] = temp;}}
补充 2:归并排序
归并排序(Merge Sort)采用分治法(Divide and Conquer)的思想(将原问题拆分成规模更小的子问题,然后递归求解),把数组拆分成子数组,先对每个子数组进行排序,然后再将有序的子数组进行合并,得到完全有序的数组。时间复杂度和空间复杂度分别为 O(nlogn) 和 O(n)。常见的将两个有序数组合并成一个有序数组的方式,称为二路归并。
下面是一段通过归并排序对数组进行升序排列的示例代码:
function mergeSort(array) {function merge(leftArr, rightArr) {var result = [];while (leftArr.length > 0 && rightArr.length > 0) {if (leftArr[0] < rightArr[0])result.push(leftArr.shift());elseresult.push(rightArr.shift());}return result.concat(leftArr).concat(rightArr);}if (array.length == 1) return array;var middle = Math.floor(array.length / 2);var left = array.slice(0, middle);var right = array.slice(middle);return merge(mergeSort(left), mergeSort(right));}
总结
本课时首先介绍了算法的两个重要效率指标:时间复杂度和空间复杂度。时间复杂度根据执行次数来计算,空间复杂度根据临时变量的大小来计算。算法的复杂度用一个带有参数的函数 O 来表示,函数 O 的参数为 n 的多项式,为了方便比较,一般只会保留 n 的最高次项并省略系数。在常见的算法复杂度中,常数复杂度最优,指数复杂度最劣。
在理解算法相关基础后重点分析了 JavaScript 的 Array.prototype.sort() 函数的底层实现算法 TimSort。TimSort 是一种混合排序算法,结合了折半插入排序和归并排序。
TimSort 算法的优化思路,其实和性能优化的思路也有异曲同工之妙,在“第 23 讲:谈性能优化到底在谈什么?”中提过,性能优化有两个方向:做减法和做除法。在 TimSort 中使用的归并排序将数据拆分 run,就带有做除法的思想,而在生成 run 的时候利用数据的有序性,这种和缓存类似的操作就是典型的做减法。
最后布置一道思考题:你在开发过程中还用到过哪些算法?欢迎在留言区分享你的经历。

