数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
在这个模块,我把常见的 “套路” 题,帮你总结成手写代码时应该准备的各种代码模板。还会把自己压箱底的独家代码模板分享给你,利用它,我多次在 10 分钟以内拿下了算法面试。
今天我先带你把数据结构部分做一个归纳和整理,方便你考前复习和平日积累。可以想象一下,如果在准备面试期间,你已经刷了很多题,那么在临近面试时还可以做些什么呢?
- 把所有写过的代码再看一遍?
- 把前面 20 讲的内容从头到尾再复习一遍?
- 还是继续刷题?
在我个人看来,以上这些方法都不可取,此时最行之有效的方法是将学过的知识尽可能地压缩、再压缩,最后形成模板。整理模板,有以下几个好处。
- 组合:其实大部分面试题都是一些算法模块的组合,并不需要我们真正去发明一个算法。
- 速度:面试写题时速度更快,一些常用的功能性代码可以直接粘贴过去,不用在打字和调试上浪费时间。
- 重点:可以在有限的时间里重点关注整理好的代码模板,告别 “大海捞针” 式的复习。
其实面试中考察的那些高频知识点,就像一块块 “积木”,而面试求解过程就像 “搭积木的游戏”。高效利用代码模版的技巧,能够帮助你在面试时写出更高效和 0 Bug 的代码。
说明:一些扩展知识点,我会通过练习题的形式给出来。
栈
在《01 | 栈:从简单栈到单调栈,解决经典栈问题》中,我们将栈的知识总结在了下面这张知识导图中。
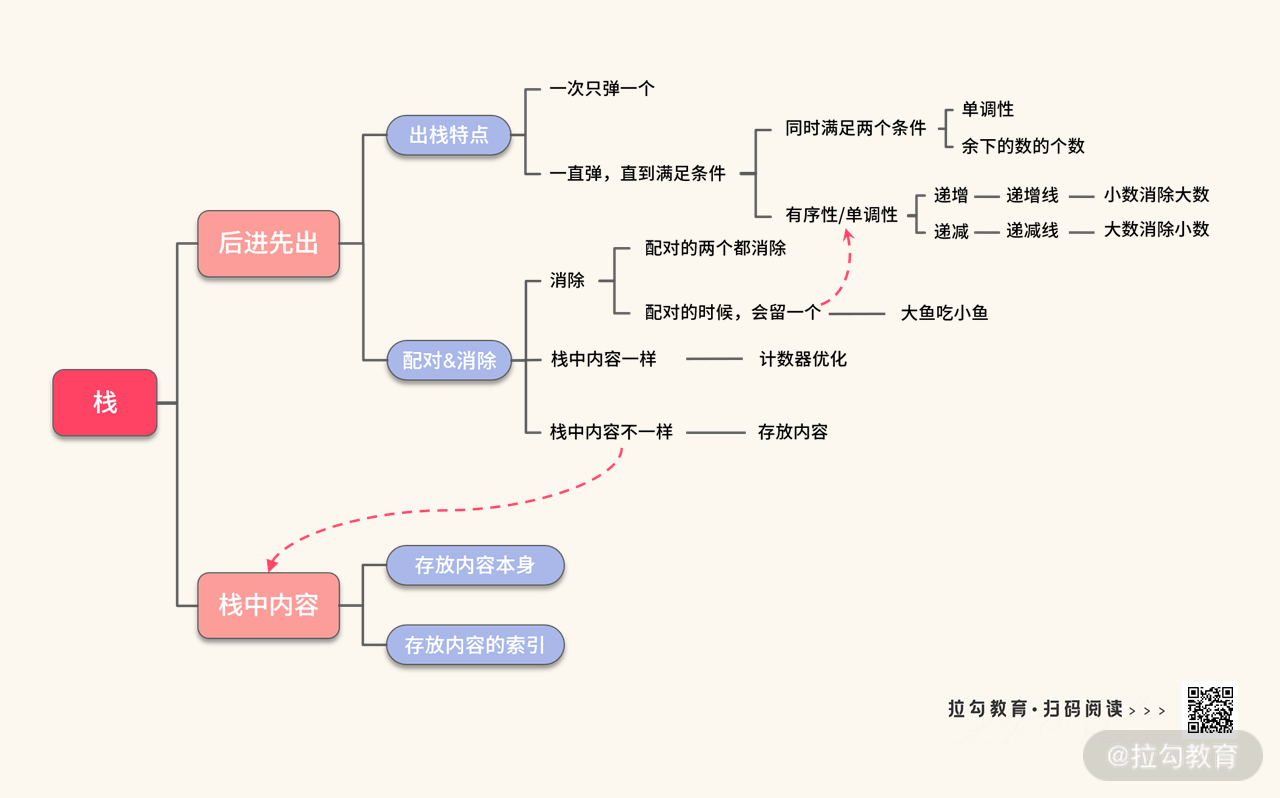
简单栈的性质
后面我们又在《20 | 5 种解法,如何利用常量空间求解最长有效括号长度?》的 “特点 4” 中,介绍了另一个栈的重点性质——括号匹配时栈的性质。我们可以用如下代码模板展示这个性质:
int longestValidParentheses(String s) {final int N = s == null ? 0 : s.length();if (N <= 1) {return 0;}Stack<Integer> st = new Stack<>();int ans = 0;int start = 0;for (int i = 0; i < N; i++) {final char c = s.charAt(i);if (c == ')') {if (st.isEmpty()) {start = i + 1;} else {st.pop();final int base =st.isEmpty() ? start : st.peek() + 1;ans = Math.max(ans, i - base + 1);}} else {st.push(i);}}return ans;}}
栈的模拟主要是使用其他数据结构来模拟栈的 push/pop 操作,主要涉及 3 个经典的题目,即下面的练习题 1、练习题 2 以及练习题 3。
练习题 1:请使用两个队列实现栈的 push/pop/empty/size 四种操作。
练习题 2:输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
练习题 3:定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
单调栈
单调栈中经常还会用来解决这类题目:数组中元素右边第一个比元素自身小的元素的位置。
int[] findRightSmall(int[] A) {int[] ans = new int[A.length];Stack<Integer> t = new Stack();for (int i = 0; i < A.length; i++) {final int x = A[i];while (!t.empty() && A[t.peek()] > x) {ans[t.peek()] = i;t.pop();}t.push(i);}while (!t.empty()) {ans[t.peek()] = -1;t.pop();}return ans;}
还有 3 类问题与上面这道题目类似,一般而言,深入理解其中一个模板即可。
- 数组中元素右边第一个比我大的元素的位置
- 数组中元素左边离我最近且比我小的元素的位置
- 数组中元素左边离我最近且比我大的元素的位置
单调栈的性质
我们将单调栈的性质总结为以下两点,更详细的介绍你可以回到《16 | 如何利用 DP 与单调队列寻找最大矩形?》进行复习。
- 当单调递增栈中存放数组下标 i, j, k 时,其中 (i, k] 中的元素 > A[j];
- 当单调递增栈中存放数组下标 i, j,并且当 A[k] 入栈,会把栈顶元素 A[j]“削” 出栈时,其中 (j, k) 元素 > A[j]。
我们曾经用到单调栈性质的模板代码求解最大矩形,如下所示:
int largestRectangleArea(int[] A) {final int N = A == null ? 0 : A.length;int top = 0;int[] s = new int[N];int ans = 0;for (int i = 0; i <= N; i++) {final int x = i == N ? -1 : A[i];while (top > 0 && A[s[top - 1]] > x) {final int height = A[s[--top]];final int rightPos = i;final int leftPos = top > 0 ? s[top - 1] : -1;final int width = rightPos - leftPos - 1;final int area = height * width;ans = Math.max(ans, area);}s[top++] = i;}return ans;}
队列
关于队列的知识点,我们同样总结在了一张思维导图中,如下所示:
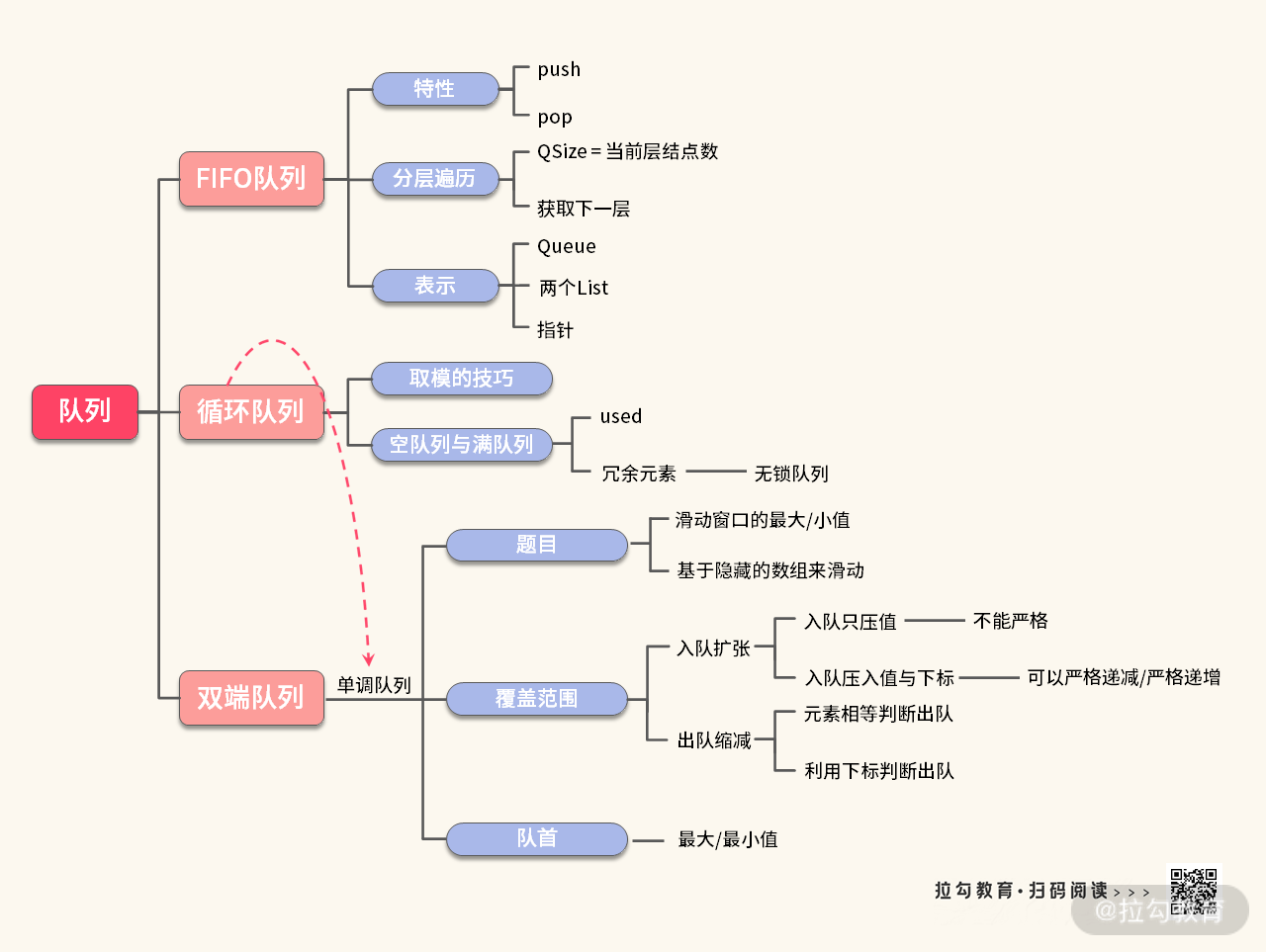
队列的数据结构知识点一般有 5 个:
- FIFO 队列
- 循环队列(模板)
- 单调队列(模板)
- 堆(模板)
- 优先级队列
不过一般而言,需要重点掌握的数据结构的模板只有 3 个,即循环队列、单调队列以及堆。
循环队列
首先我们看一下使用数组来实现循环队列的写法,代码如下:
class MyCircularQueue {private int used = 0;private int front = 0;private int rear = 0;private int capacity = 0;private int[] a = null;public MyCircularQueue(int k) {capacity = k;a = new int[capacity];}public boolean enQueue(int value) {if (isFull()) {return false;}a[rear] = value;rear = (rear + 1) % capacity;used++;return true;}public boolean deQueue() {if (isEmpty()) {return false;}int ret = a[front];front = (front + 1) % capacity;used--;return true;}public int Front() {if (isEmpty()) {return -1;}return a[front];}public int Rear() {if (isEmpty()) {return -1;}int tail = (rear - 1 + capacity) % capacity;return a[tail];}public boolean isEmpty() {return used == 0;}public boolean isFull() {return used == capacity;}}
单调队列
接下来,我们看一下单调队列的实现代码。单调队列有两种,即递增队列和递减队列。由于这两种队列的代码模版非常类似,因此只需要记住其中一个就可以了,递减队列代码如下:
class Solution {private ArrayDeque<Integer> Q = new ArrayDeque<Integer>();private void push(int val) {while (!Q.isEmpty() && Q.getLast() < val) {Q.removeLast();}Q.addLast(val);}private void pop(int val) {if (!Q.isEmpty() && Q.getFirst() == val) {Q.removeFirst();}}
此外,单调队列还可以使用 “<元素值,下标> 同时入队和出队” 的方法来实现。这两种实现本质上没有太大的区别。你可以根据你对单调队列理解程度选择一种作为做通用模板。
堆
由于堆往往用来实现优先级队列,因此,这里我也整理好了堆的实现的代码:
class Heap {private int[] a = null;private int n = 0;public void sink(int i) {int j = 0;int t = a[i];while ((j = (i << 1) + 1) < n) {if (j < n - 1 && a[j] < a[j + 1]) {j++;}if (a[j] > t) {a[i] = a[j];i = j;} else {break;}}a[i] = t;}public void swim(int i) {int t = a[i];int par = 0;while (i > 0 && (par = (i - 1) >> 1) != i) {if (a[par] < t) {a[i] = a[par];i = par;} else {break;}}a[i] = t;}public void push(int v) {a[n++] = v;swim(n - 1);}public int pop() {int ret = a[0];a[0] = a[--n];sink(0);return ret;}public int size() {return n;}}
链表
要想解决链表题,我们首先需要掌几种最基本的操作,如下图所示:
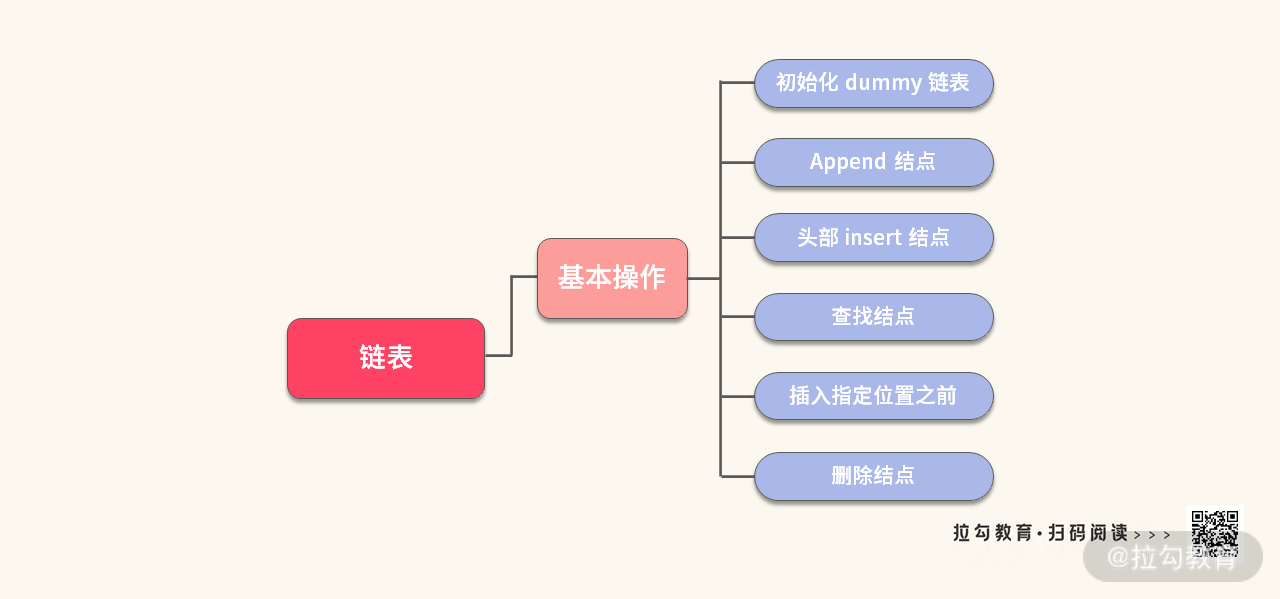
不知道你是否还记得,我在《04 | 链表:如何利用 “假头、新链表、双指针” 解决链表题?(上)》中,将这几种操作整理成了一个代码模板。其核心思想就是链表的 “第一斧”:假头。如下所示:
class MyLinkedList {class ListNode {public int val = 0;public ListNode next = null;public ListNode() {}public ListNode(int x) {val = x;}}private ListNode dummy = new ListNode();private ListNode tail = dummy;private int length = 0;public MyLinkedList() {}private ListNode getPreNode(int index) {ListNode front = dummy.next;ListNode back = dummy;for (int i = 0; i < index; i++) {back = front;front = front.next;}return back;}public int get(int index) {if (index < 0 || index >= length) {return -1;}return getPreNode(index).next.val;}public void addAtHead(int val) {ListNode p = new ListNode(val);p.next = dummy.next;dummy.next = p;if (tail == dummy) {tail = p;}length++;}public void addAtTail(int val) {tail.next = new ListNode(val);tail = tail.next;length++;}public void addAtIndex(int index, int val) {if (index > length) {return;} else if (index == length) {addAtTail(val);return;} else if (index <= 0) {addAtHead(val);return;}ListNode pre = getPreNode(index);ListNode p = new ListNode(val);p.next = pre.next;pre.next = p;length++;}public void deleteAtIndex(int index) {if (index < 0 || index >= length) {return;}ListNode pre = getPreNode(index);if (tail == pre.next) {tail = pre;}length--;pre.next = pre.next.next;}}
此外,关于链表,我们还需要掌握另外的 “两板斧”。这里我已经将知识点整理如下:
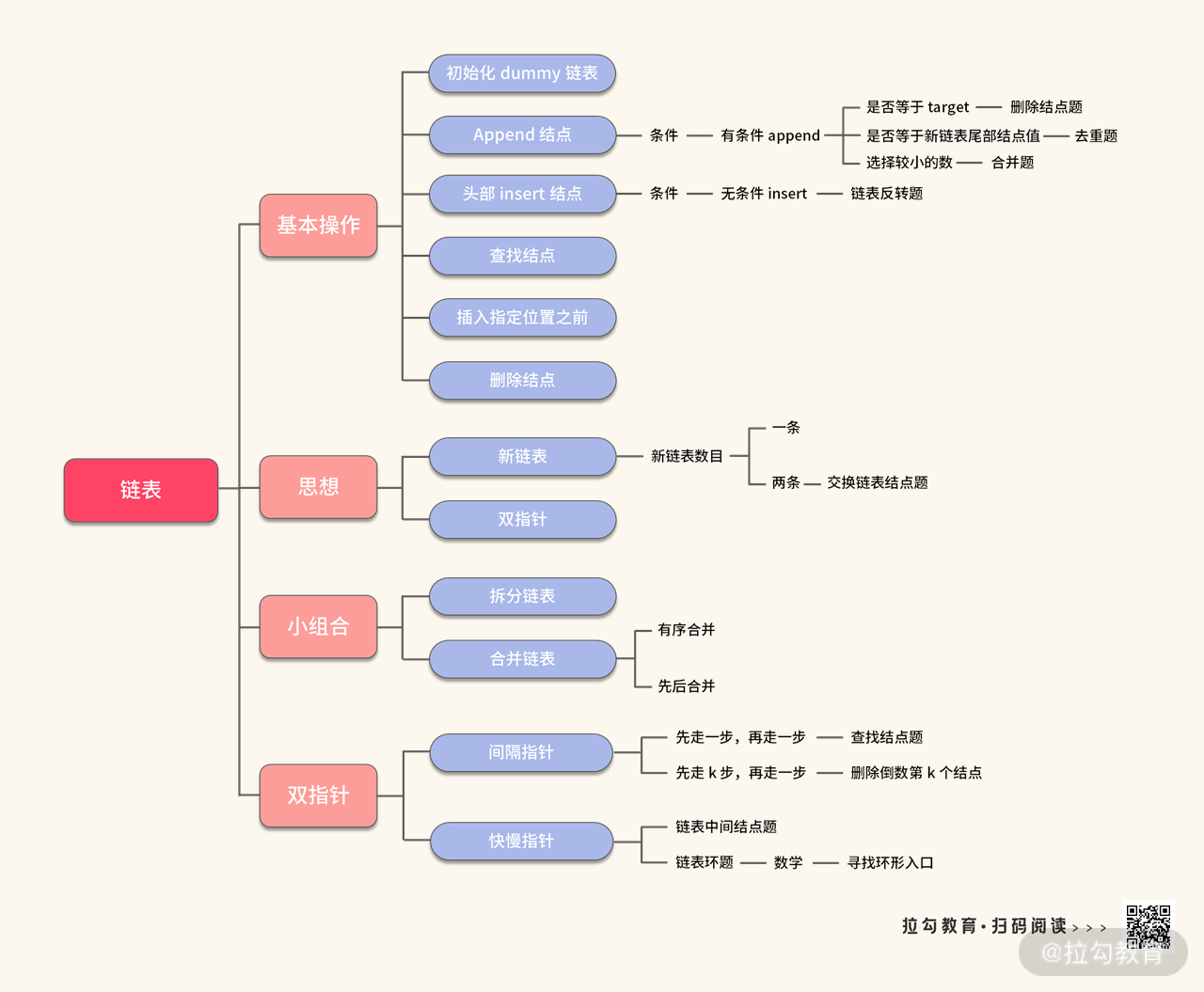
树
在《06 | 树:如何深度运用树的遍历?》中,我们深入探讨了三种遍历,并且发现只要我们掌握这三种遍历的模板代码,就能够轻松解决二叉树问题。
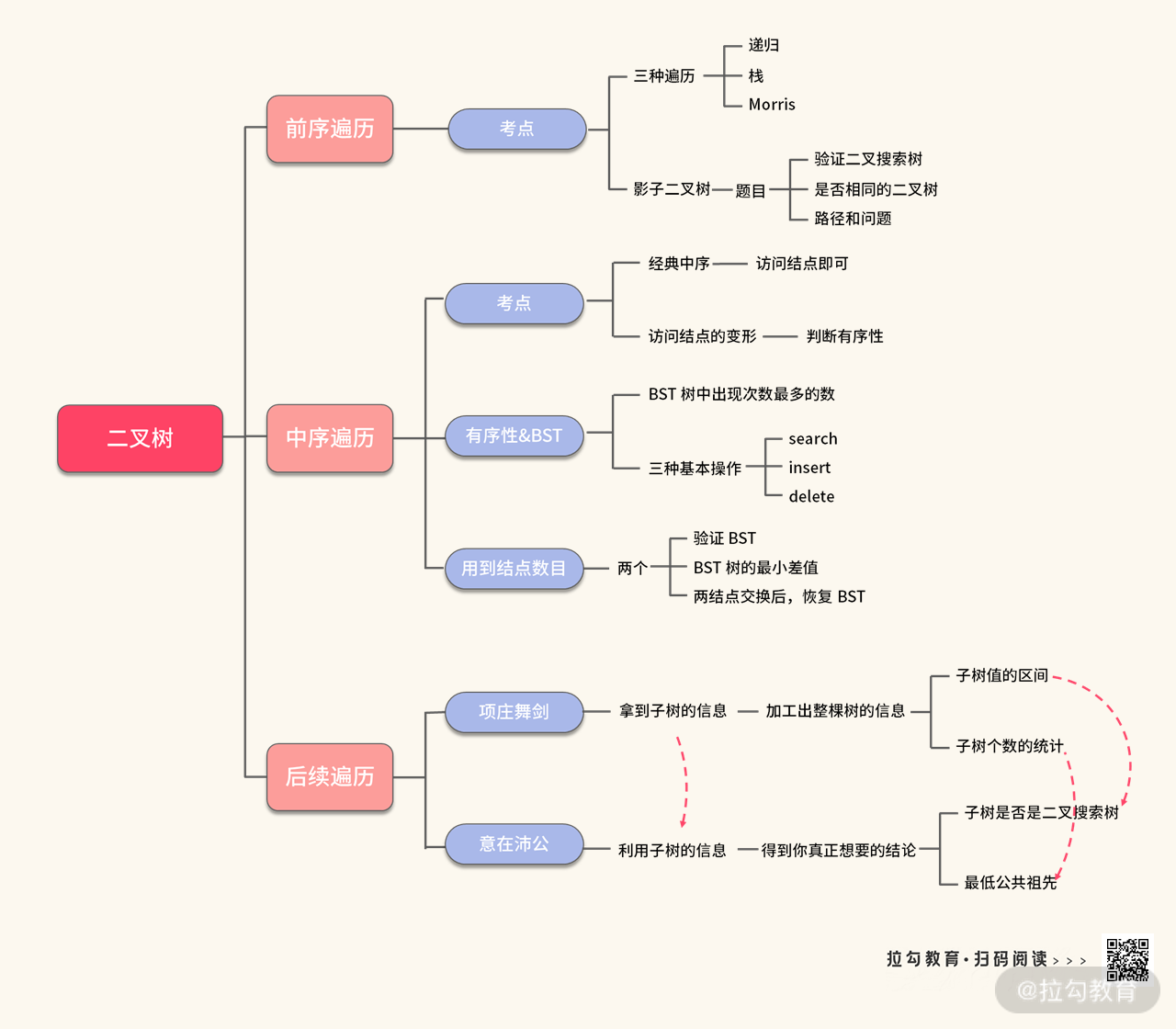
在这一讲中,我们需要熟练掌握三种遍历的代码模板有 6 个:
- 前序遍历的递归实现与栈的实现
- 中序遍历的递归实现与栈的实现
- 后序遍历的递归实现与栈的实现
下面我们分别整理一下。
前序遍历
采用递归的前序遍历的代码如下(解析在注释里):
void preOrder(TreeNode root, List<Integer> ans) {if (root != null) {ans.add(root.val);preOrder(root.left, ans);preOrder(root.right, ans);}}
使用栈来实现的前序遍历的代码如下(解析在注释里):
class Solution {public List<Integer> preorderTraversal(TreeNode root) {Stack<TreeNode> s = new Stack<>();List<Integer> ans = new ArrayList<>();while (root != null || !s.empty()) {while (root != null) {s.push(root);ans.add(root.val);root = root.left;}root = s.peek();s.pop();root = root.right;}return ans;}}
中序遍历
采用递归的中序遍历代码如下(解析在注释里):
void preOrder(TreeNode root, List<Integer> ans) {if (root != null) {preOrder(root.left, ans);ans.add(root.val);preOrder(root.right, ans);}}
采用非递归的中序代码(解析在注释里):
class Solution {public List<Integer> inorderTraversal(TreeNode root) {Stack<TreeNode> s = new Stack<>();List<Integer> ans = new ArrayList<>();while (root != null || !s.empty()) {while (root != null) {s.push(root);root = root.left;}root = s.peek();s.pop();ans.add(root.val);root = root.right;}return ans;}}
后序遍历
采用递归实现的后序遍历代码模板如下(解析在注释里):
void postOrder(TreeNode root, List<Integer> ans) {if (root != null) {postOrder(root.left, ans);postOrder(root.right, ans);ans.add(root.val);}}
采用非递归的后序遍历代码如下(解析在注释里):
class Solution {public List<Integer> postorderTraversal(TreeNode t) {List<Integer> ans = new ArrayList<>();TreeNode pre = null;Stack<TreeNode> s = new Stack<>();while (!s.isEmpty() || t != null) {while (t != null) {s.push(t);t = t.left;}t = s.peek();if (t.right == null || t.right == pre) {ans.add(t.val);s.pop();pre = t;t = null;} else {t = t.right;}}return ans;}}
【面试建议】在面试的时候,大部分情况都应该优先写递归的代码,除非面试官特别要求你必须使用 “非递归” 来实现。主要有以下几点原因:
- 递归代码更加简单,因此不容易出错;
- 不要为了 “炫技” 展示 “非递归” 代码;
- 如果我们要进行二叉树上的搜索、DP、二分等情况的时候,“非递归” 的代码往往会增加代码的复杂度,面试的时候不容易完全写对。
并查集
虽然并查集的代码模板只有一个,但是涉及的知识点却不少,这里我们将重点的内容浓缩在下面这张图里:
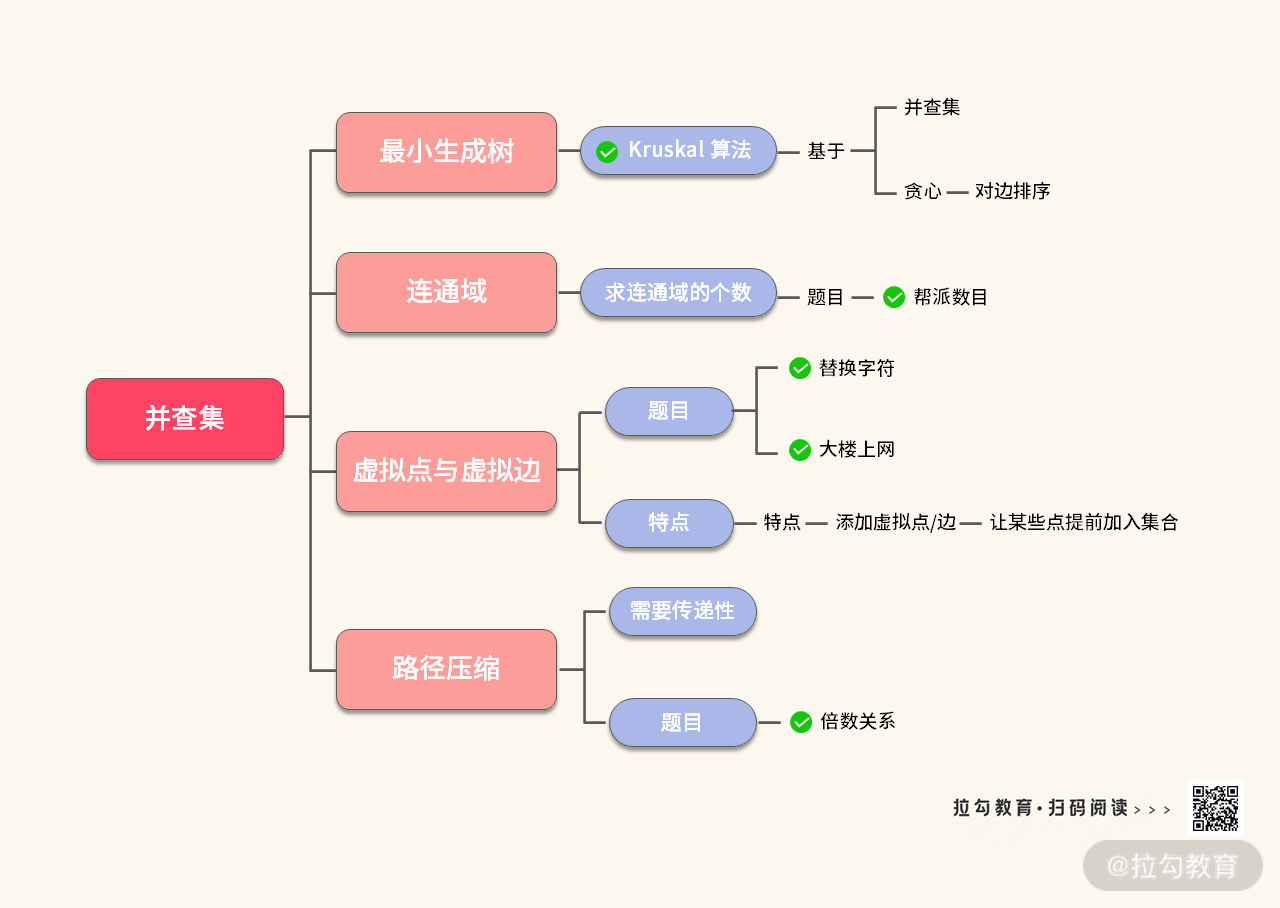
最后,我们给出并查集的代码模板如下(解析在注释里):
class UF {int[] F = null;int count = 0;int[] Cnt = null;void Init(int n){F = new int[n];Cnt = new int[n];for (int i = 0; i < n; i++) {F[i] = i;Cnt[i] = 1;}count = n;}int Find(int x){if (x == F[x]) {return x;}F[x] = Find(F[x]);return F[x];}void Union(int x, int y){int xpar = Find(x);int ypar = Find(y);if (xpar != ypar) {F[xpar] = ypar;Cnt[ypar] += Cnt[xpar];count--;}}int Size(int i) {return Cnt[Find(i); }}
总结
在这一讲中,我们通过整理代码模板,将 “第 01 讲” 到“第 07 讲” 学习的所有知识点都整理好了。这样你复习起来是不是压力要小很多呢。下面我再和你分享两个代码模板的“小秘密”。
模板代码要精练
其实在整理模板的时候,要尽量将代码压缩得越短越好(指的并不是不换行),代码压缩得短,有以下好处:
- 如果是自己熟悉的代码,在需要记忆的情况下,越短越好记;
- 较短的代码可以更精练,一眼看上去没有那么大的心理压力。
比如就我自己而言,在复习并查集的代码时,就经常使用下面这段更短的代码:
int Find(int x) { return x == F[x] ? x : F[x] = Find(F[x]); }void Union(int x, int y) { F[find(x)] = find(y); }
自己整理可复用的代码模版
和你分享一下自己整理的模板的好处。主要是基于以下两点原因。
1. 变量的命名要有规律,而这些规律都是自己平时约定使用的,当你复习代码时会更熟练,比如:
1)返回值一律设置为 ans 或者 ret;
2)遍历下标设置为 i,j,k;
3)长度变量设置为 len。
2. 同一个算法往往有很多种写法,自己的写法会更熟悉,而且可以不断迭代和复用。
所以,本讲的练习题,就是希望你能把 “第 01 讲” 到“第 07 讲”刷过的题的代码整理成模板。当临近面试,你只需要对着思维导图和代码模板过一下思路就可以了。
这一讲我们就介绍到这里。下一讲介绍《23 | 算法模板:如何让高频算法考点秒变默写题?》,让我们继续前进。

