10 | 双指针：如何掌握最长、定长、最短区间问题的解题决窍？

数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育

双指针的使用方法，在前面学习链表的时候，已经有所涉及。不过在那时，主要介绍的快慢指针。在这一讲，我们主要介绍双指针在数组上的应用。

双指针，通常是命名用两个指针在数组 / 链表上遍历，然后解决满足某种性质的区间问题。在链表中我们已经介绍过双指针（也可以叫作快慢指针）。不过今天我们将重点介绍：如何利用双指针处理以下 3 方面的区间问题：

• 最长区间
• 定长区间
• 最短区间

学完本讲，你将收获双指针的 3 个模板，帮助你通杀所有面试中可能碰到的双指针题目。Ready, Go Go!

双指针基础

考察双指针的题目，绝大多数题眼就在区间。见面不含糊，直接尝试挖出题目的两个特点：

1. 弄清楚题目要的是什么样的区间？是最长，定长，最短这三种里面的哪一种。
2. 区间需要满足的条件是什么？

如果发现题目符合这两个特点，还需要让题目中的连续子串（后文区间 = 连续子串）符合单调性。让我们一起看一下什么是单调性。

注：这里的双指针只是一种算法的命名，有的人喜欢叫滑动窗口，或者尺取法。我觉得用双指针更加形象一点。“指针” 二字并不能对应到 C/C++ 里面的指针类型。在使用的时候，往往是两个下标。

单调性

使用双指针，需要区间满足一个条件：区间状态的单调性。这里可以用一个例子进行描述。比如我们想在如下数组中找到小于等于 6 的最长子串。现在只看以 3 为区间最右端元素的各种情况，如下图所示：

那么区间可以分为 3 种：

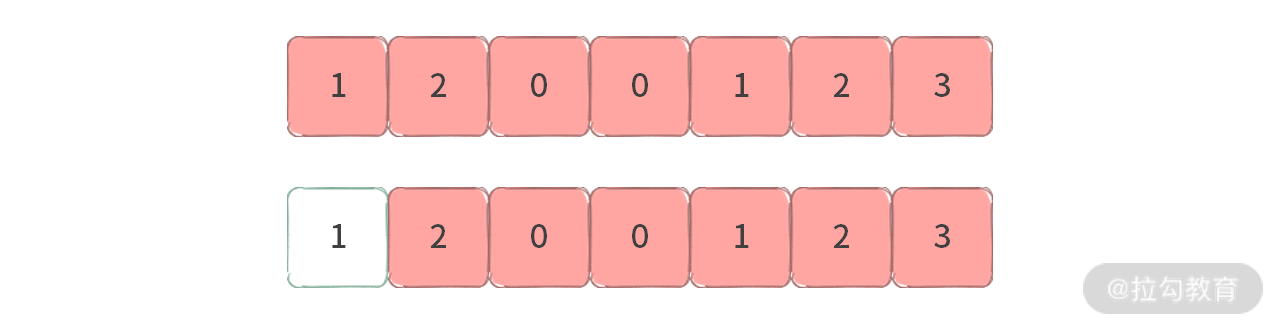
第一种区间：以 3 为右端，其和大于 6。

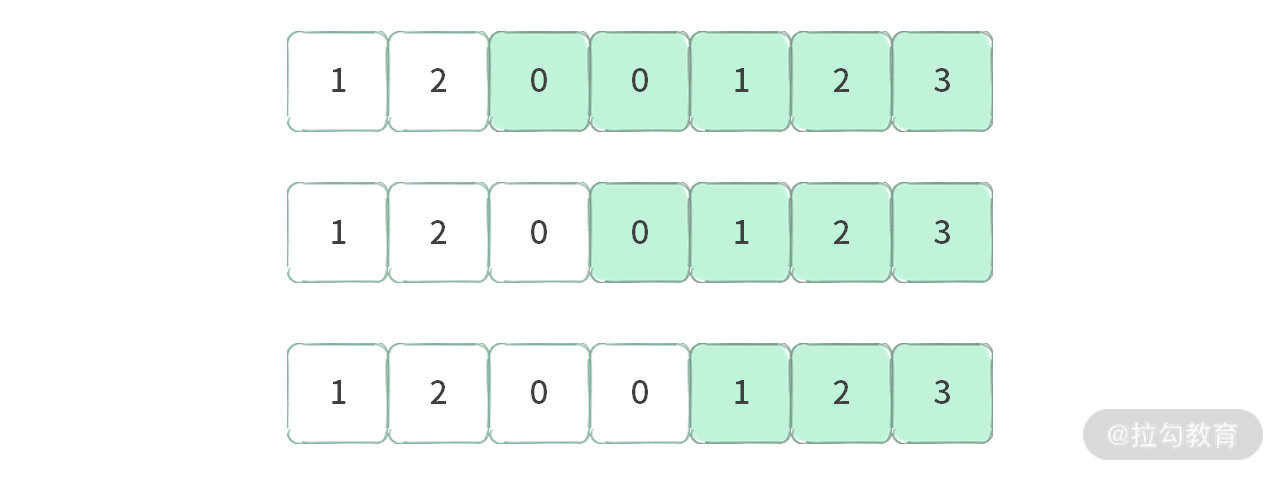
第二种区间：以 3 为右端的区间，其和等于 6。

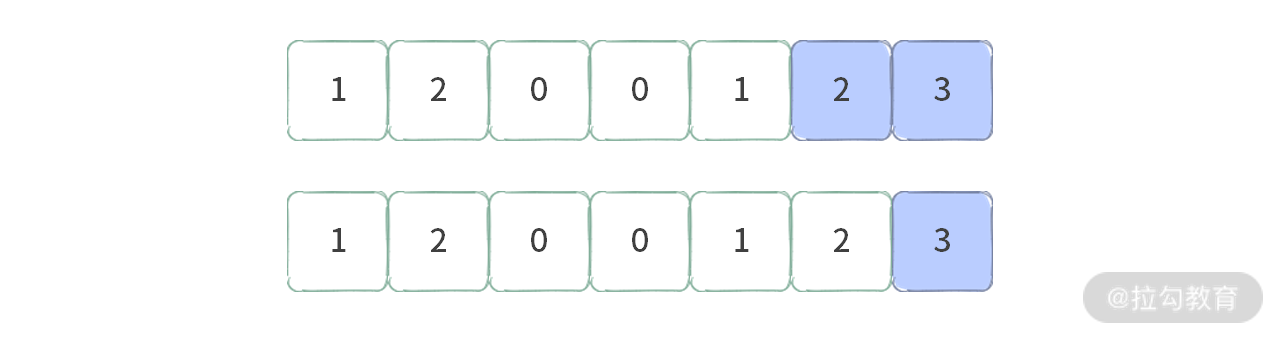
第三种区间：以 3 为右端的区间，其和小于 6。

如果我们将这些区间的累计和呈现到数轴上，就会得到如下图所示的一个图像：

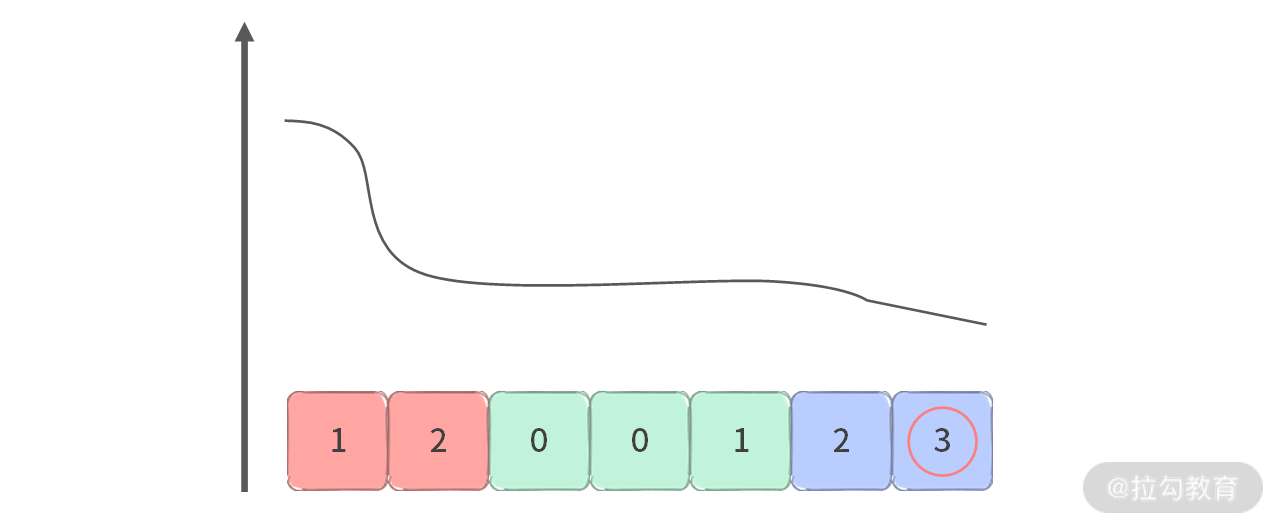
可以看出，区间的状态的变化是单调的，并且是连续的：这就是双指针算法使用的条件。

有个快速判断区间属性是否满足单调性的办法，那就是，当往区间里面添加元素的时候，不能出现波折，比如不允许 “满足条件→不满足条件→满足条件” 的情况。

比如，我们这里的限定条件改成：需要区间满足 >= 6。我们看一下如下操作步骤：

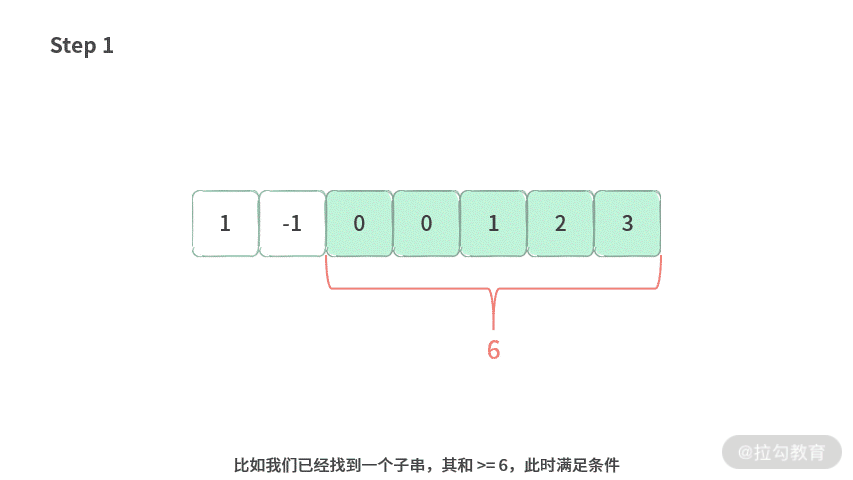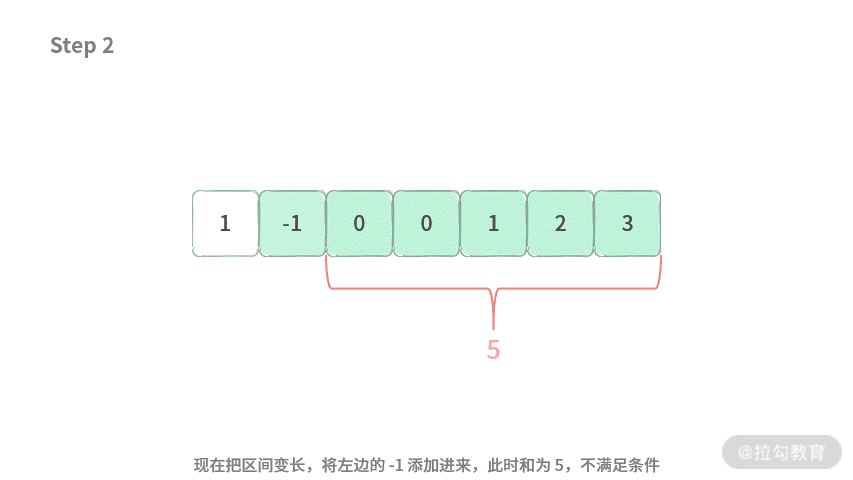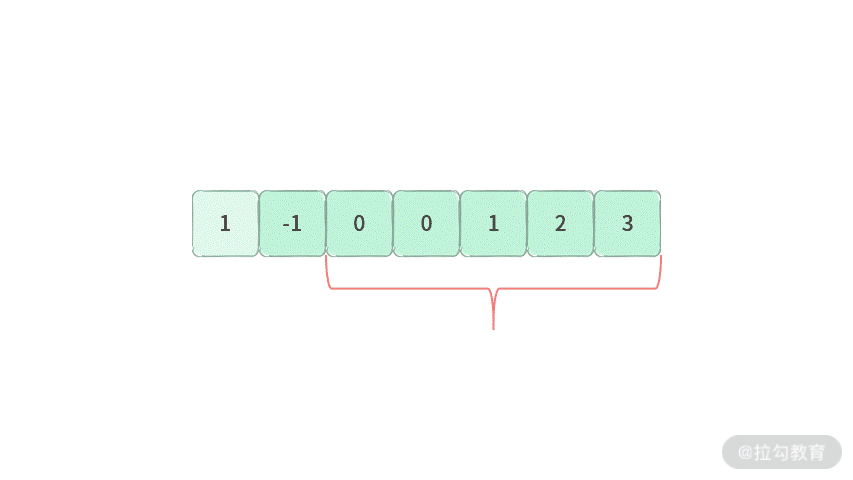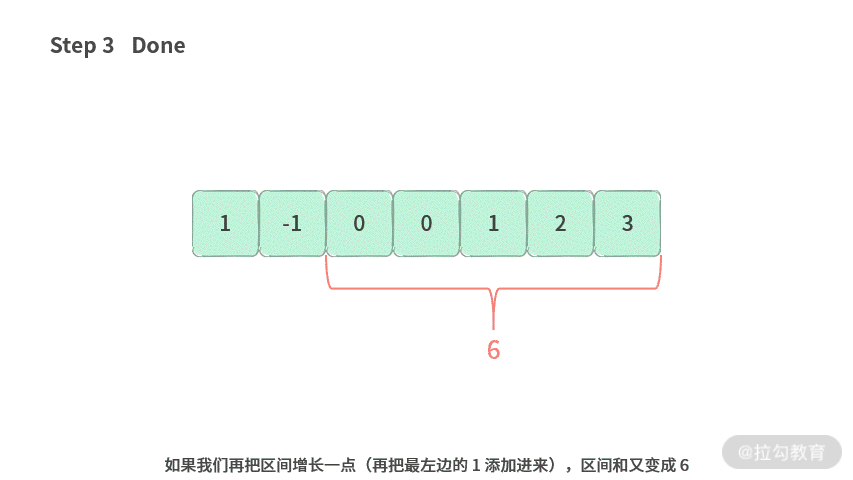
那么区间的状态变化就是 “满足条件→不满足条件→满足条件”。这样就不符合单调性。

工作原理

那么双指针为什么可以在 O(N)？它的合理性在哪？这里我尽量尝试用最直白的语言来把题目证明一下。

首先我们来看区间右端固定集合（这个名词是我自创的，因为我没有找到相关的术语来描述这种非常基础的操作）：

把 A[i] 元素固定为区间的右端点，只变动区间的左边界形成的所有区间，并且按区间长度需要从长到短排列。

比如要遍历如下数组：

int[] A = new int{1,2,3,4};

比如以 A[i = 2] = 3 为例，形成的区间右端固定集合为：

如果对每个元素找到区间右端固定集合，我们同样可以遍历一个数组里面的所有的子区间：

i = 0, A[0] = 1 => [1]
i = 1, A[1] = 2 => [1, 2], [2]
i = 2, A[2] = 3 => [1, 2, 3], [2, 3], [3]
i = 3, A[3] = 4 => [1, 2, 3, 4], [2, 3, 4], [3, 4], [4]

接下来我们只分析 A[i] 元素的区间右端固定集合。比如要找出和 <= 7 的最长区间。当已经处理到 A[2] = 3 的时候，当发现 [1, 2, 3] 这个区间之和 6 已经 <=7 时（满足要求），实际上就没有必要再去处理 [2, 3] 区间和 [3] 区间。因为我们要的就是最长区间！

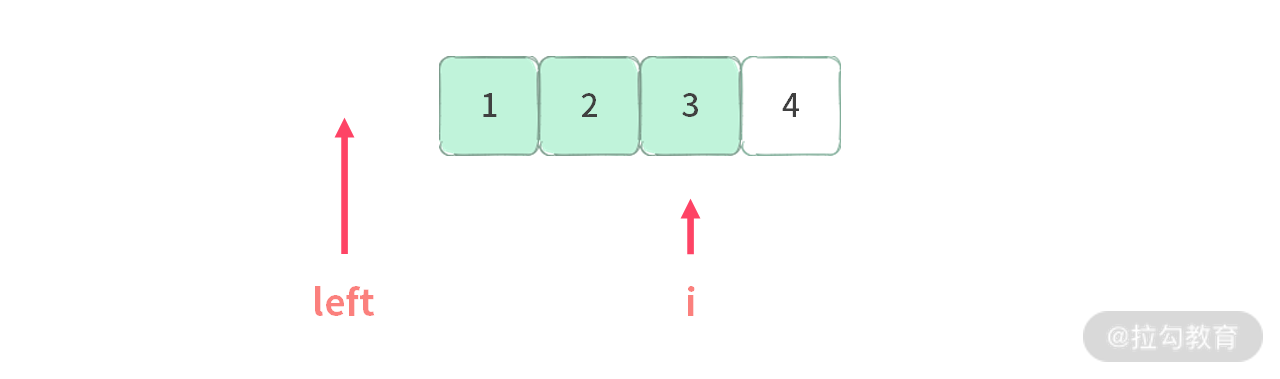
通过上述分析，我们可以总结一个区间最优原则：从左向右遍历区间右端固定集合中的每个区间，找到一个满足条件的解即可停止。

利用这个性质，我们可以再加一个指针 left, 指向区间的左边，与 A[i] 元素构成区间 (left, i]，注意这里我们又用到了开闭原则，只不过此时是左开右闭。那么寻找以 A[i] 为右边界的最优解可以分 3 步走：

step1. 将A[i]加到区间中，形成新区间(left, i]
step2. while (left < i && (left,i]区间不满足要求) {
  left++;
}
step 3. (left, i]区间满足要求

前面我们已经找到了 A[2] = 3 的合法最长区间为 (-1, 2]，那么接下来看一下如何再接着处理 A[3] = 4。

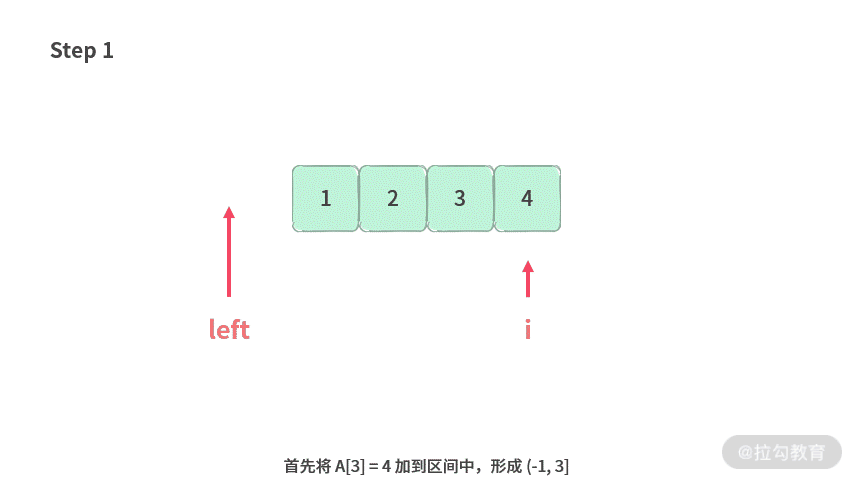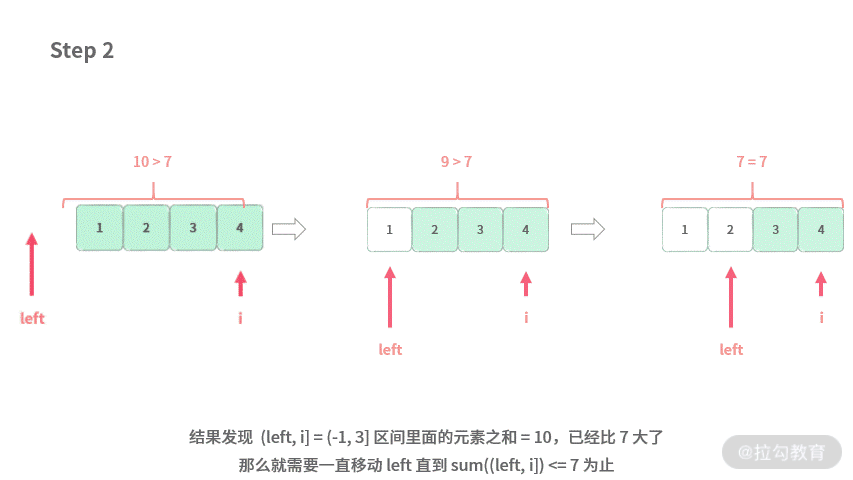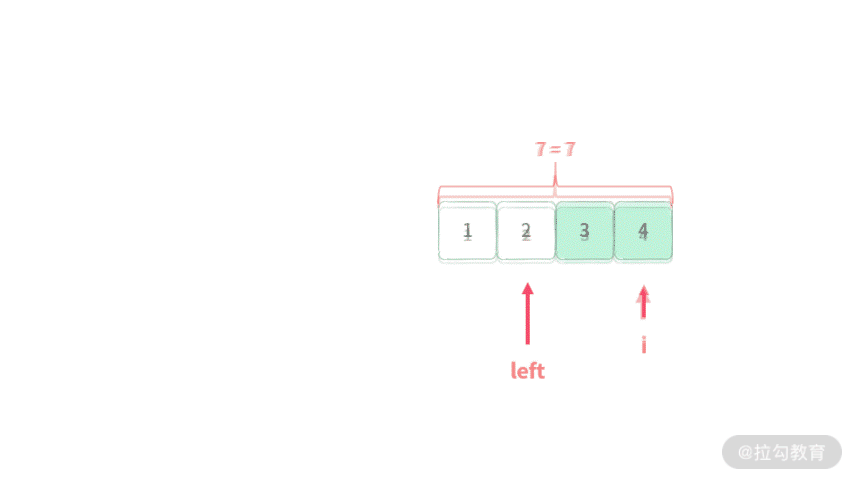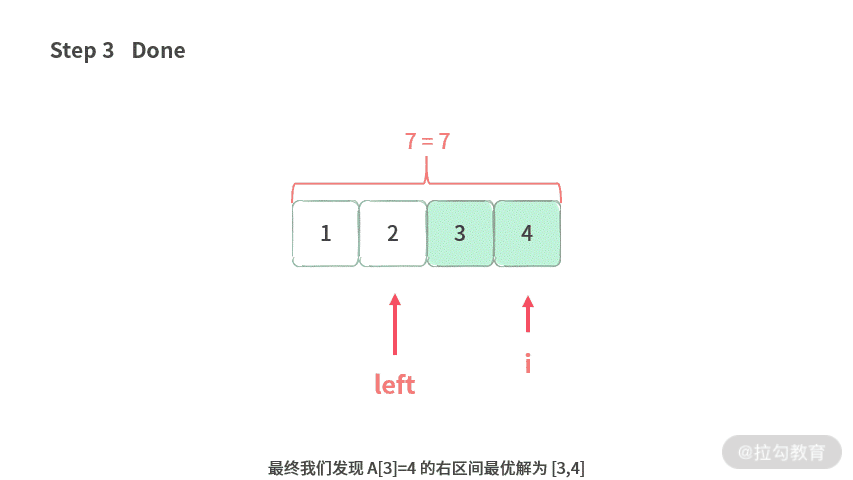
通过上述分析，我们可以拿出求解最长区间时双指针的结论：最长区间问题的最优解→只需要遍历每个元素 A[i] 的最优解即可。

以前面给的 A[2] = 3, A[3] = 4 两个元素为例，在找整个最优解的时候，只需要看两个区间：

• [1, 2, 3]
• [3, 4]

我们发现，在寻找最优解的时候，已经比暴力算法少了很多需要查看的区间。

最长区间

使用双指针算法来解决最长区间的问题，一般题目需要具备如下特点：

• 给定一个条件
• 求最长区间 / 最长子串
• 题目给出的区间需要具备单调性

这里需要特别指出，不是看到题目要求最长子串 / 最长区间就使用双指针，而是需要题目的求解空间具有单调性。这是一个非常重要具必备的条件。

面试必杀技

不过，真正在面试的时候，可没有那么多时间让你慢慢去证明，慢慢去推导。放心，我这里已经给你准备好了最长区间的面试必杀技，关键就两招：

1. 两个指针，left 指针和 right 指针，两个指针形成的区间为 (left, right]。这里的开闭原则是左开右闭；
2. 惰性原则，如果把 left 指针当成一个人，那么这个人是非常懒惰的，他总是要等到火烧屁股（条件不满足了）才向右移动。

求最长区间的代码模板大概会长成这样（解析在注释里）：

int maxLength(int[] A) {
int N = A.length;
int left = -1;
int ans = 0;
for (int i = 0; i < N; i++) {
while (check((left, i]))) {
      ++left; 
    }
    ans = max(ans, i - left);
  }
return ans; 
}

好了，我们的刀已经磨好了，下面就开始准备切题吧。注意上方代码中的两个 “TODO”，我们已经把写算法题，变成填空题了。

例 1：不含重复字符的最长区间

【题目】找出一个字符串 s 中无重复字符子串的长度。

输入： s = “abcdc”

输出：4

解释：因为最长的子串就是 “abcd”

【分析】首先看题目的特点：

• 求最长子串
• 条件为无重复字符
• 单调性

子串是数组的一个区间。那么题目的特点已经和最长区间的特点非常匹配了。再看单调性，当子串在变长的时候，不可能出现 “无重复字符 → 重复字符 → 无重复字符” 这种可能。因此满足单调性。

那么这里我们直接使用双指针进行求解。

其实可以直接套用前面总结出的模板，但是我们立马会发现模板中代码并不完整，还有两个 “TODO” 需要处理。下面我们看一下如何像处理填空题一样把这两个空给填上。

1. 检查区间状态

while (check((left, i]))是否满足条件)

首先，我们检查区间是否满足条件，那么如何检查？当我们把新字符 s[i] 加入合法区间 (left, i-1]，形成 (left, i] 区间之后，区间的状态就会变成如下图所示的样子：

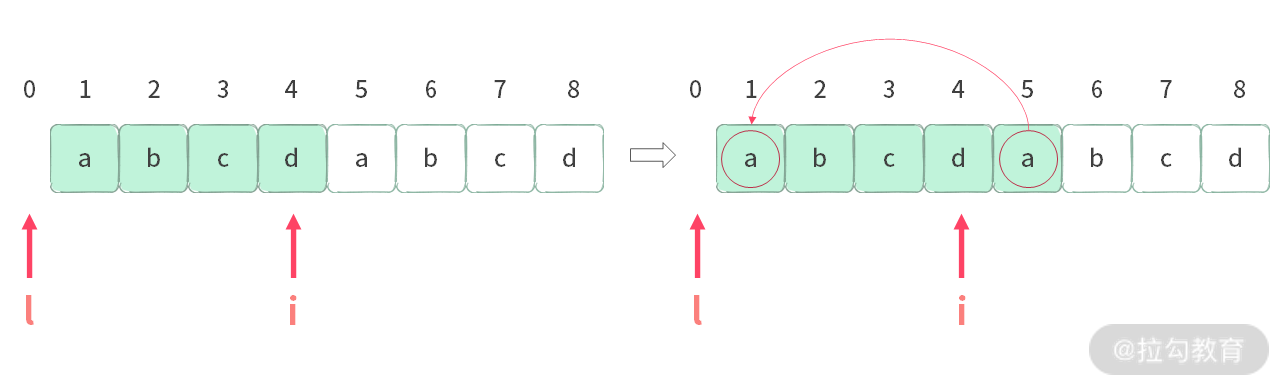
这个时候，可以发现区间里面 (left, i] 里面已经有一个’a’了。也就是说：如果我们发现当加入一个字符的时候，这个字符位置在 (left, i-1] 区间里面，此时就产生了重复字符。所以检查条件可以修改成：

while (left < i && pos[字符] > left) {
}

2. 修改区间状态

我们来看一个例子，当产生重复字符的时候，如何修改呢？具体操作如下：

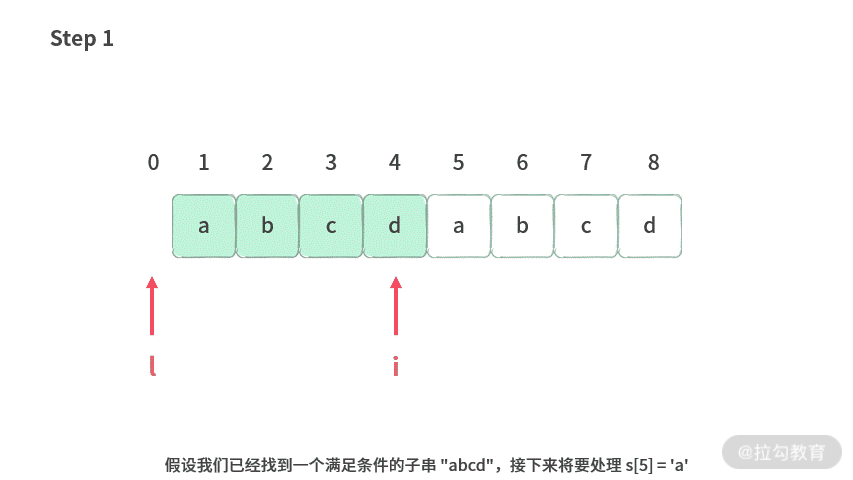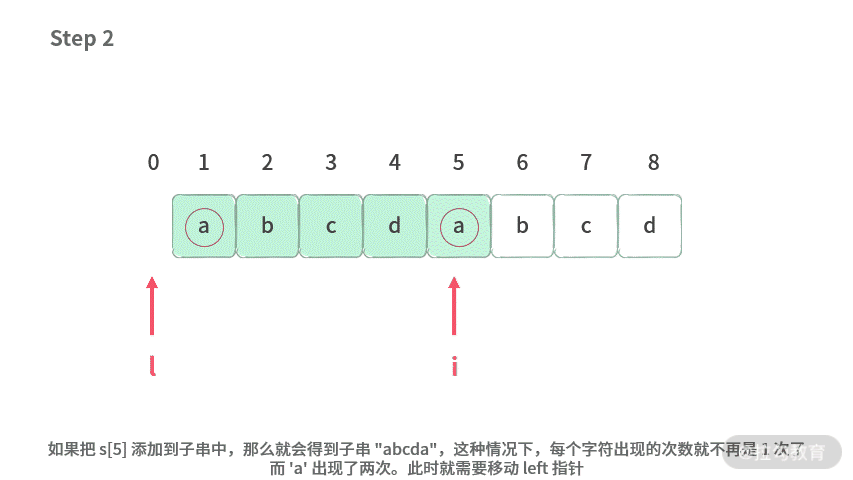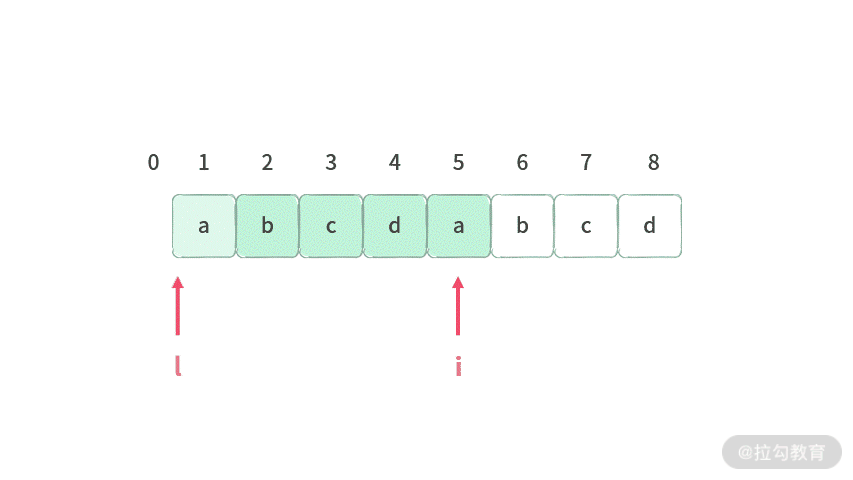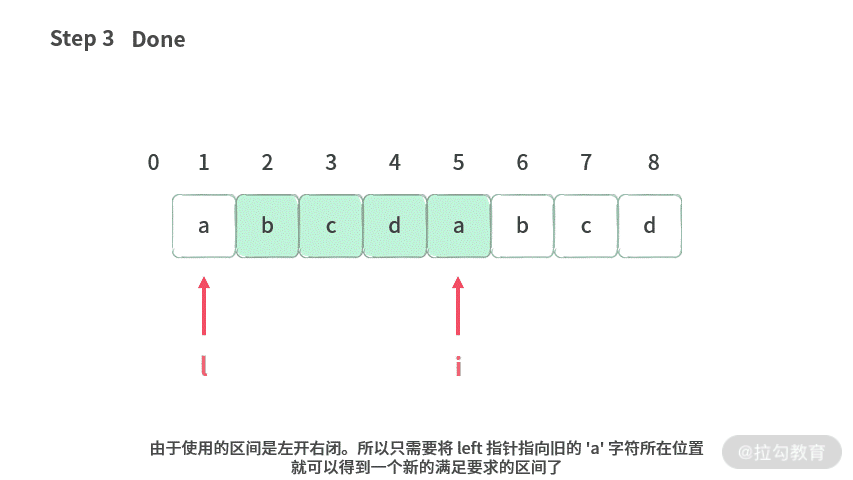
也就是 left = pos[‘a’] 就可以。那么状态的更新就可以写成如下：

while (left < i && pos[字符] > left) {
  left = pos[字符];
}

【代码】填好空的代码如下（解析在注释里）：

int lengthOfLongestSubstring(String s) {
final int N = s == null ? 0 : s.length();
int[] pos = new int[256];
  Arrays.fill(pos, -1);
int ans = 0;
int left = -1;
for (int i = 0; i < N; i++) {
final int idx = (int)s.charAt(i);
while (pos[idx] > left) {
      left = pos[idx];
    }
    pos[idx] = i;
    ans = Math.max(ans, i - left);
  }
return ans;
}

代码：Java/C++/Python

复杂度分析：时间复杂度 O(N)，空间复杂度 O(1)。

【小结】到这里，我们已经学习了最长区间的原理，模板，以及将它巧妙地变成填空题来快速破题。

关于最长区间问题，我们可以总结如下：

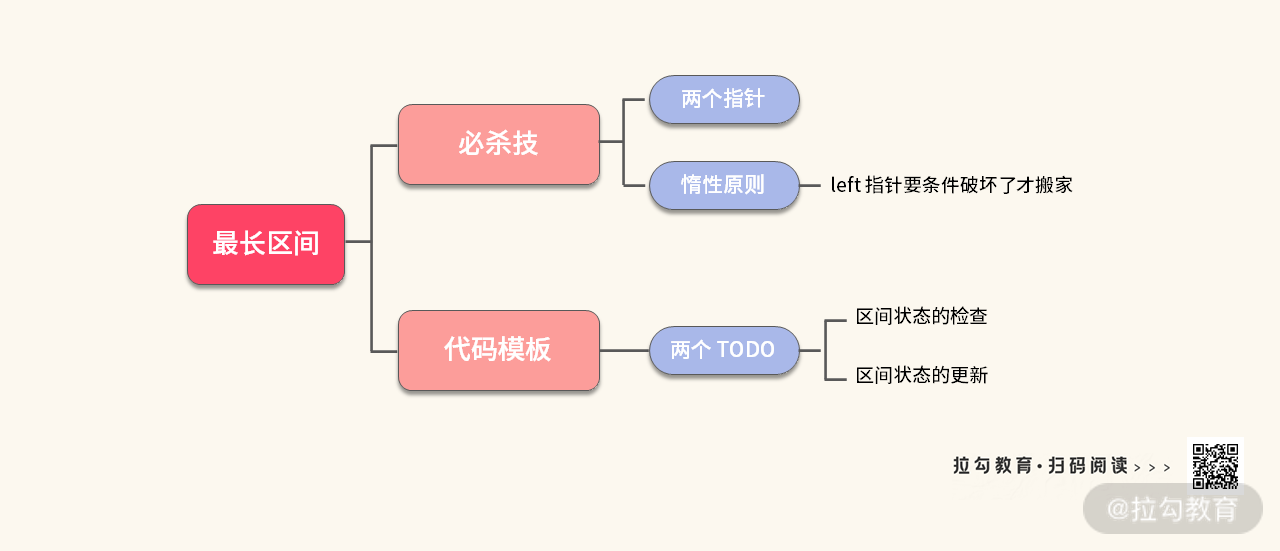
接下来，为了巩固已学的知识，我们再一起看几道练习题。

练习题 1：给定一个字符串，你可以把字符串里面的某些字符替换成任意字符 k 次。请返回你可以得到的最长相同字符的长度。

输入：s = ‘ABACD’, k = 1

输出：3

解释：只需要把’ABA’ 里面的 B 替换成’A’ 即可。

代码：Java/C++/Python

练习题 2：你需要实现一个类，实现里面的 insert(char c) 函数，调用者会通过 insert 接口给你一个字符。此外，调用者还会立马调用 firstAppearingOnce() 函数来查询第一个出现的字符。如果不存在，返回 ‘#’ 字符。

输入：google

输出：ggg#ll

代码：Java/C++/Python

练习题 3：给定一个数组 A[]，请你找到一个最长区间，这个区间里面最多包含两个不一样的数。

输入：A = [1, 2, 1, 2, 3]

输出：4

解释：区间 [1, 2, 1, 2] 里面只有两个数，并且是最长区间。

代码：Java/C++/Python

练习题 4：在练习题 3 的基础上，做了一点点扩展，最多包含 k 个不一样的数。

代码：Java/C++/Python

练习题 5：一个数组里面的数总是增增减减，会出现升序，然后再降序的情况，请找出这个数组里面最长的子串，这个子串刚好形成先升后降的大山峰。

代码:Java/C++/Python

最长区间问题，经过一小点改动还可以用来解决区间计数问题。下面我们一起来看一下。

例 2: 区间计数

【题目】给定一个正数数组 A[]，以及一个正整数 k，求乘积小于 k 的子数组的个数。

输入：A = [100, 1, 1, 1, 2, 3, 4], k = 6

输出：12

解释：乘积小于 6 的子数组一共有 12 个。比如 [1]、 [1]、[1,1,1]，等等。

【分析】前面我们介绍的是使用模板求解最长区间，这道题目问题却是在求区间的个数。那么这两者之间有什么联系呢？

这里我们只看 A[4] = 2 元素的区间右端固定集合。如下所示：

A[3] = 2:
[100, 1, 1, 1, 2]
     [1, 1, 1, 2] <-- 最优解：乘积 < 6的最长区间
        [1, 1, 2]
           [1, 2]
              [2]

可以发现，[1, 1, 1, 2] 是我们寻找最长区间时候的最优解。让我们再回想一下前面提到的区间最优原则：

区间右端固定集合合里面，一旦找到一个最优解，那么最优解右边的区间如果满足条件，但都不是最优解。

区间最优原则也在疯狂暗示我们，如果找到以 A[i] 为右端的最优解，那么余下的更短的以 A[i] 为右端的区间，也是满足小于等于 k 的。在统计的时候，我们只需要累计每个 A[i] 的最优解区间的长度就可以了。

那么区间计数的模板就变成如下所示的样子（解析在注释里）：

int rangeCounter(int[] A) {
int N = A.length;
int left = -1;
int ans = 0;
for (int i = 0; i < N; i++) {
while (check((left, i]))) {
      ++left; 
    }
    ans += i - left;
  }
return ans; 
}

好吧，经过上述一番分析，我们又把区间计数问题变成填空题。下面只需要再填好那两个 “TODO” 的地方就可以了：

• 区间状态是否满足条件
• 移动左指针的时候，修改区间的状态

根据题意，这两个都是比较好填的：

• 区间状态，我们直接用累积就可以了
• 条件的判断只需要 s > k
• 当移动左指针的时候，只需要 s /= A[++left] 即可

【代码】填好空的代码如下（解析在注释里）：

int numSubarrayProductLessThanK(int[] A, int k) {
final int N = A == null ? 0 : A.length;
int left = -1;
long ans = 0;
long s = 1;
for (int i = 0; i < N; i++) {
long x = A[i];
    s *= x;
while (s >= k && left < i) {
      s /= A[++left];
    }
    ans += i - left;
  }
return (int)ans;
}

代码：Java/C++/Python

复杂度分析：时间复杂度 O(N)，空间复杂度 O(1)。

【小结】这里我们再次提到区间最优原则，这个原则非常重要，是使用双指针来解决问题的关键与依赖。你可以尝试求解下面这道练习题，细细体会该原则。

练习题 6：给定一个有正数也有负数的数组 A[] 和 k，请找到最长的子数组，其和等于 k。

解法 1：Java/C++/Python

注：这里可能需要你好好想一下，为什么不能使用我们刚才所讲的模板。

下面我们整理一下最长区间题目的特点，以及代码模板的适用条件：

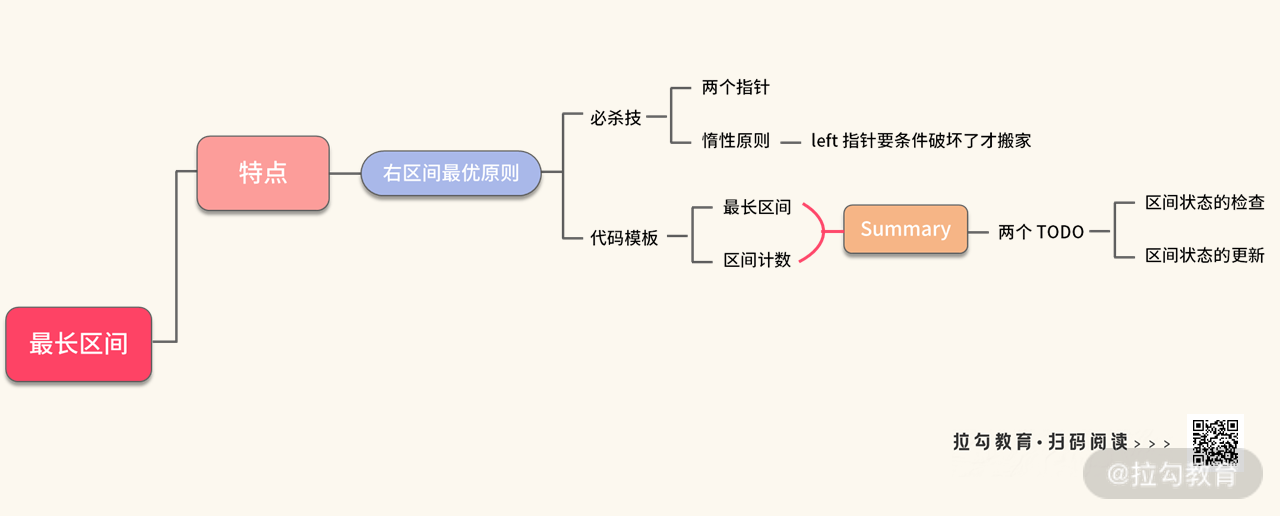
最长区间的知识点就讲到这里。接下来我们看一下定长区间问题的求解。

定长区间

定长区间问题是要找到一个固定长度的区间，并且这个区间必须满足某种条件。所以求解定长区间问题，实质上是需要找满足两个条件的子串。

1. 子串的长度固定。由于长度固定，因此，定长区间问题不需要满足单调性。
2. 子串必须满足某种条件。

定长区间的解法通常也被称为 “滑动窗口算法”。在 “第 09 讲”讲解二分搜索 “例 4: 最大平均值” 的时候，我们对这种方法有涉及，但是并没有深入地详细展开。这里我们再总结一下这种算法的模板与套路。

定长区间，由于长度固定，你可以想象成有一个固定的长度的窗口在数组上滑动。比如有一个长度为 3 的窗口在一个数组上滑动。

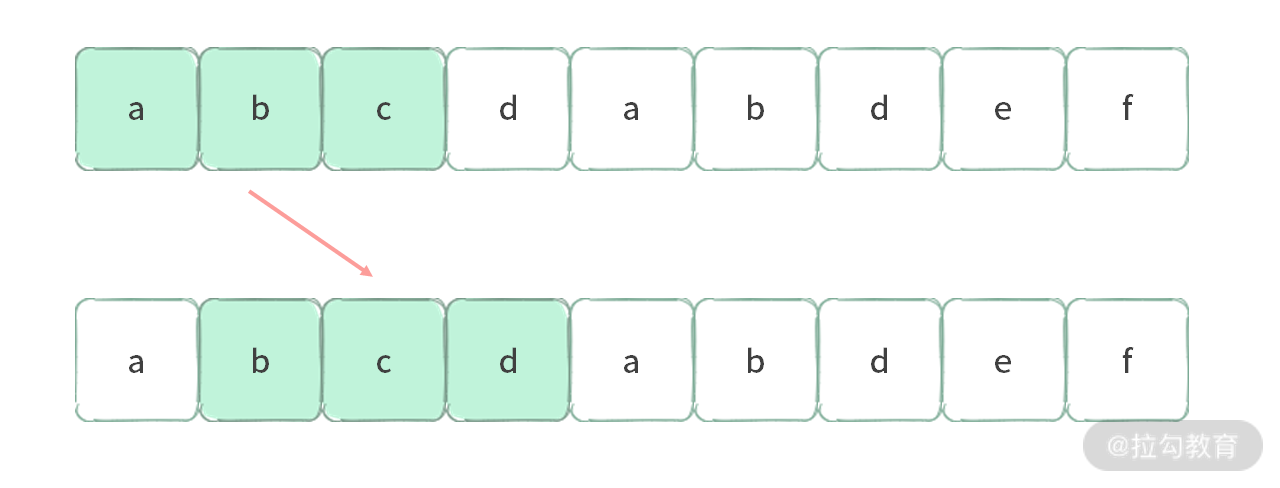
写定长区间的代码也比较容易。如果我们比较两者的变化，可以发现，只有首尾元素发生了变动。

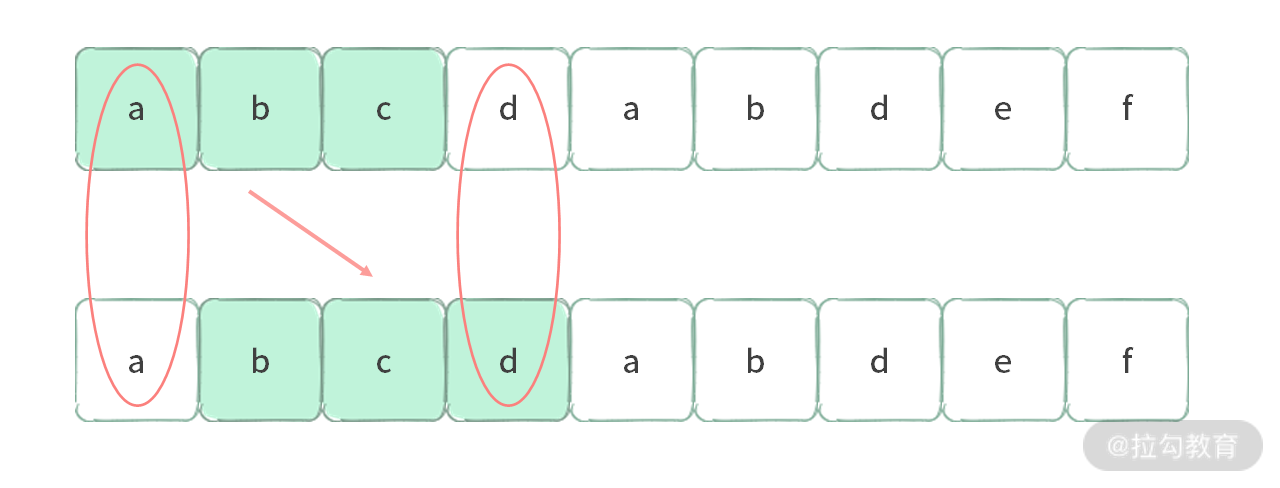
那么我们在处理时，只需要保证加入元素和删除元素的时候，去更新区间的性质，查看是否满足约束条件即可。

面试必杀技

在面试的时候，如果拿到题目再去慢慢想滑动窗口应该怎么写，会浪费不少时间。这里我已经给你总结好了方法，你拿到题的时候，需要从题目中分析两个特点。

1. 固定长度：题目要求解的是不是一个固定长度的子串？
2. 约束条件： 这个定长区间必须要满足什么性质？

如果从题目中分析出以上 2 个特点，那么基本上可以直接套用定长区间的 “滑动窗口” 解法了。这里我已经整理好了一个通用的模板，如下所示：

int fixedLength(int[] A, int windowSize) {
final int N = A == null ? 0 : A.length;
int left = -1;
for (int i = 0; i < N; i++) {
if (i - left < windowSize) {
continue;
    }
    left++;
  }
return ans; 
}

注意，模板中只有3 个 “TODO”要根据题目的具体情况来填。这样，我们又把定长区间算法题变成了填空题。接下来我们再拿两道题来试刀。

例 3: 定长子串 1

【题目】给定两个字符串 A，B。判断 B 字符串是否有包含 A 字符串的任意排列。

输入：A = “ab”, B = “bac”

输出：true

解释：因为 B 字符串是包含 “ba”，而 “ba” 是字符串 “ab” 的一个排列。

【分析】首先我们看题目的特点，A 字符串的任意排列，透露出两个特点：

1. 任意排列的长度肯定等于 A.length()
2. 任意排列的字符的数目的统计结果必然相同

从这两个特点，我们可以知道：

• 固定长度，并且区间的长度就是 A 字符串的长度；
• 约束条件，区间里面的字符的统计个数必须相等。

如果现在我们直接套用模板，并且直接用数组来统计字符个数。就可以写出如下代码了（解析在注释里）：

boolean checkInclusion(String A, String B) {
final int blen = B == null ? 0 : B.length();
final int alen = A == null ? 0 : A.length();
int[] astat = new int[256];
for (int i = 0; i < alen; i++) {
    astat[A.charAt(i)]++;
  }
int[] bstat = new int[256];
int left = -1;
for (int i = 0; i < blen; i++) {
    Character c = B.charAt(i);
    bstat[c]++;
if (i - left < alen) {
continue;
    }
boolean same = true;
for (int j = 0; j < 256 && same; j++) {
      same = astat[j] == bstat[j];
    }
if (same)
return true;
    left++;
    bstat[B.charAt(left)]--;
  }
return false;
}

我们发现，套用模板还是挺好求解的。不过这里面还有一个小问题，在对比统计结果的时候，我们采用的方式比较暴力，总是遍历了统计结果里面的每一项。那么有没有更好的办法呢？

不难发现，需要比较的 astat 与 bstat，其中 A 字符串的统计结果astat 是固定不变的。并且 bstat 里面的统计结果，每次仅有一项会发生增减 1的情况。那么我们可以采用这种办法：

• equal = 0，表示一开始只有 0 项字符的统计结果是相等的；
• 当 bstat[x]++ 之后。如果发现 bstat[x] == astat[x]，那么证明其中又有一个字符的统计结果满足要求了，equal ++；
• 如果发现 equal 等于需要统计的字符个数，那么就得到了一个正确的解；
• 在滑动窗口的尾巴移除之前，如果 bstat[x] == astat[x]，那么说明我们要把一个统计结果相等的字符给删除掉，equal—。

为了方便你记忆，我把这四个办法总结为一句话，那就是：“刚好等于 astat[x] 时进行增 / 减”。这样我们就可以写出更加高效的代码了，不需要再去逐个对比统计结果里面的每一项是否相等。

【代码】最终优化后的代码如下（解析在注释里）：

class Counter extends astatashMap<Character, Integer> {
public int get(Character k) {
return containsKey(k) ? super.get(k) : 0;
  }
public void add(Character k, int v) {
    put(k, get(k) + v);
if (get(k) <= 0) {
      remove(k);
    }
  }
}
boolean checkInclusion(String A, String B) {
final int blen = B == null ? 0 : B.length();
final int alen = A == null ? 0 : A.length();
  Counter astat = new Counter();
for (int i = 0; i < alen; i++) {
    astat.add(A.charAt(i), 1);
  }
  Counter bstat = new Counter();
int left = -1;
int equal = 0;
for (int i = 0; i < blen; i++) {
    Character c = B.charAt(i);
    bstat.add(c, 1);
if (bstat.get(c) == astat.get(c)) {
      equal++;
    }
if (i - left < alen) {
continue;
    }
if (equal == astat.size()) {
return true;
    }
    left++;
    Character rm = B.charAt(left);
if (bstat.get(rm) == astat.get(rm)) {
      equal--;
    }
    bstat.add(rm, -1);
  }
return false;
}

代码：Java/C++/Python

复杂度分析：时间复杂度 O(N)，空间复杂度 O(1)。由于字符个数是固定的 256 个。虽然使用了哈希表，但是占用的空间是固定的。因此，空间复杂度为 O(1)。

【小结】接下来我们看一下定长区间的知识结构：

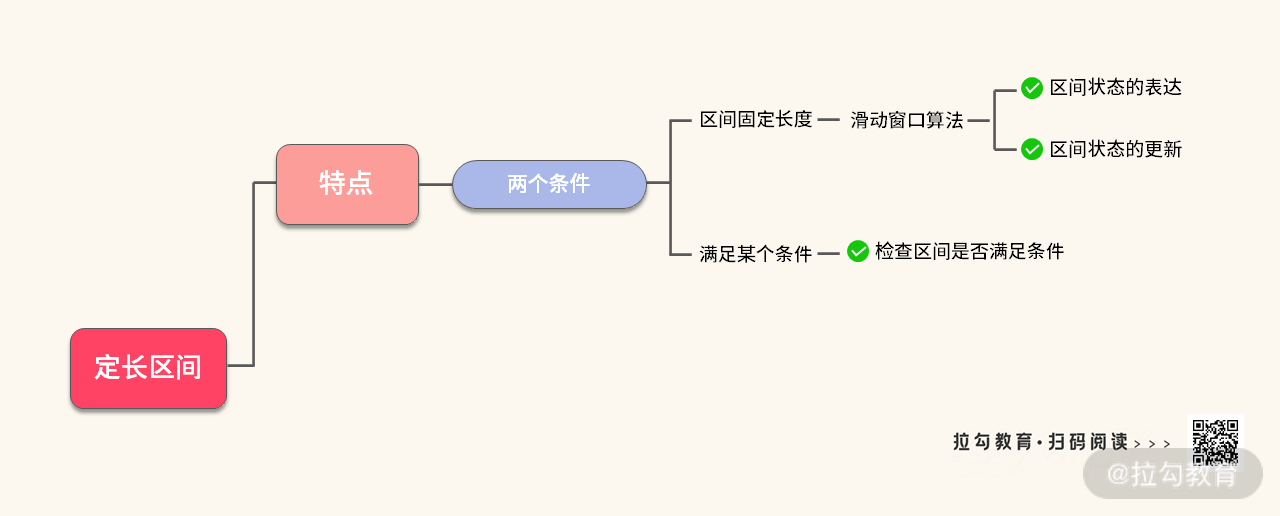
通过上图的总结我们可以发现：定长区间的核心问题就是关注区间状态的表达。所以，这道题目的考点也非常明确：

• 如何用统计的办法来表达区间的状态
• 如何验证两个哈希表是否相等

这里我再给你留个小练习，不要偷懒，一定要尝试自己解答！

练习题 7：在例 3 中我们使用了哈希表来处理字符的统计，主要是为了 Counter 类的通用性。由于字符只有 256 个。你能用数组来加速这个算法吗？

代码：Java/C++/Python

接下来我们看一下这道题目的一个变形。

例 4: 定长子串 2

【题目】给定一个字符串 s，以及一个相同长度的单词列表。请找到所有的子串，这些子串必须包含列表中所有的单词（单词的顺序可以乱）。所有符合要求的子串的起始位置。

输入：s = “AABBCCBBAA”, D = {“AA”, “BB”};

输出：[0, 6]

解释：在 s 字符串中，以下标 0 和下标 6 起始的子串 “AABB”, “BBAA” 符合要求。

【分析】每个单词的长度是固定的，设为 L，那么需要把 s 按长度 L 进行切分。那么当 L = 2 的时候，切分方式可以如下：

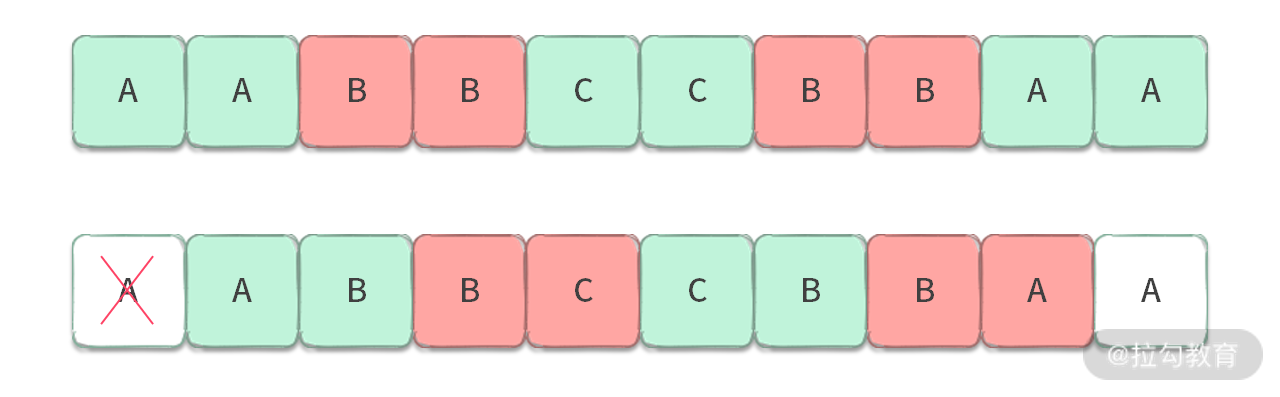
其他的切分方式都是这两种切分方式的子集。更进一步，我们可以有如下切分结论：字符串 s 要按固定长度 L 切分时，只有 L 种切分方式。

不同的切分方式，就好像生成了不同的数组一样，如下图所示：

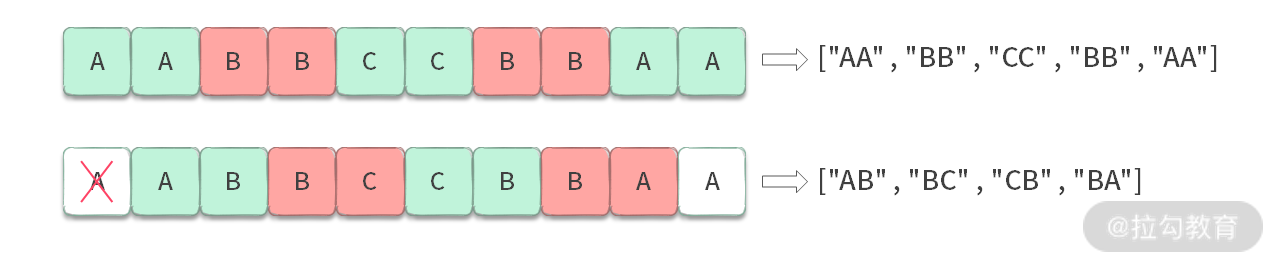
这个操作代码可以写成如下（解析在注释里）：

for (int start = 0; start < L; start++) {
for (int i = start; i + L <= s.length(); i+= L) {
    String tmp = s.substring(i, i + L);
  }
}

到此时，题目已经变成在 String[] 数组里面找一个子串，这个子串里面包含列表中所有的单词。这么一看，不就是我们前面学习过的例 3 吗。但是与例 3 不同的地方在于：

• 这里表面上看是一个字符串 s，实际上是通过字符串 s 生成 L 个数组；
• 例 3 中需要统计的是单个的字符，而在这里需要统计的是单词。

【代码】我们直接基于例 3，再加上一些代码（解析在注释里），就可以解决这道题了：

class Counter extends HashMap<String, Integer> {
public int get(String k) {
return containsKey(k) ? super.get(k) : 0;
  }
public void add(String k, int v) {
    put(k, get(k) + v);
if (get(k) <= 0) {
      remove(k);
    }
  }
}
List<Integer> findSubstring(String s, String[] D) {
  Counter H = new Counter();
int wordLength = 0;
for (String w : D) {
    wordLength = w.length();
    H.add(w, 1);
  }
  List<Integer> ans = new ArrayList<>();
for (int start = 0; start < wordLength; start++) {
    Counter R = new Counter();
int left = start - wordLength;
int equalCount = 0;
int counter = 0;
for (int i = start; i + wordLength <= s.length();
            i += wordLength) {
      String tmp = s.substring(i, i + wordLength);
      R.add(tmp, 1);
if (R.get(tmp) == H.get(tmp)) {
        equalCount++;
      }
      counter++;
if (counter < D.length) {
continue;
      }
if (equalCount == H.size()) {
        ans.add(left + wordLength);
      }
      left += wordLength;
      String rm = s.substring(left, left + wordLength);
if (R.get(rm) == H.get(rm)) {
        equalCount--;
      }
      R.add(rm, -1);
    }
  }
return ans;
}

代码：Java/C++/Python

复杂度分析：当单词固定长度为 L 的时候，一共会切分出 L 个数组。每个数组上的单词个数为 N/L，滑动窗口遍历单个数组时间复杂度是 O(N/L)，所以最终时间复杂度为 O(N)。空间复杂度由于使用了哈希表，等价于单词的个数。

【小结】到这里，我们再总结一下这个题目的考点：

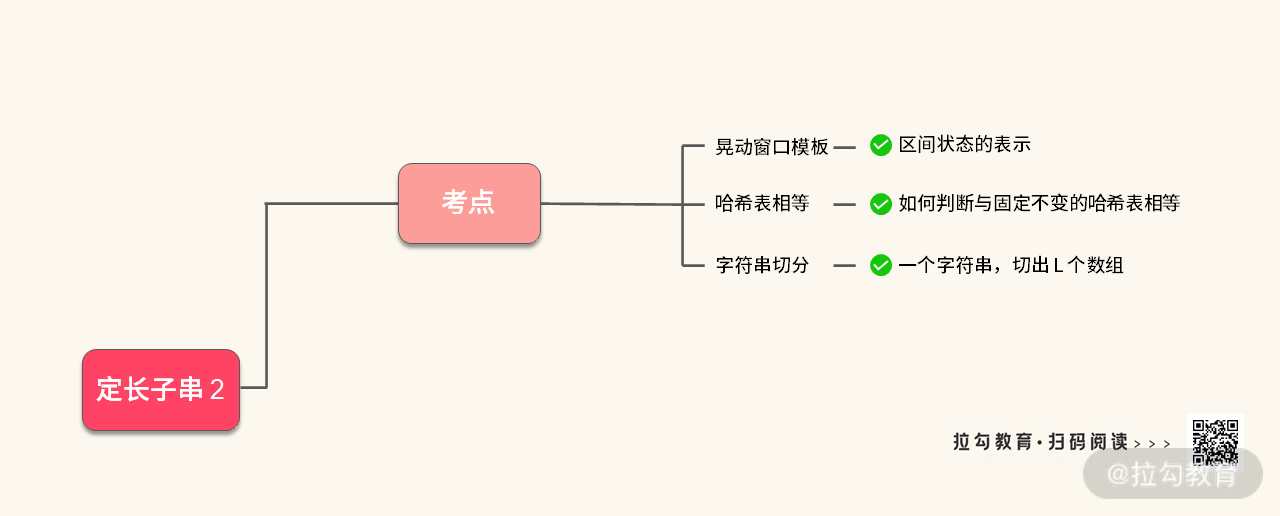
我们可以发现，在面试中，只要掌握上图中总结的三个知识点，就可以顺利地解决这道面试题。

接下来我们看一下最短区间问题。

最短区间

在区间问题中，还有一类区间问题。那就是求最短区间。这类面试题的特点也很明确：

1. 要求子串必须满足某个条件
2. 要求子串的长度越小越好

要特别注意的是，最短区间问题，也必须满足单调性。

面试必杀技

不过，在真正面试的时候，可没有那么多时间让你慢慢去证明，慢慢去推导。放心，我这里已经给你准备好了最短区间的面试必杀技，关键就两招：

1. 两个指针，left 指针和 right 指针，这两个指针形成的区间为 (left, right]，这里的开闭原则是左开右闭；
2. 积极原则，如果把 left 指针当成一个人，那么这个人是非常积极的，他总是主动积极地破坏区间已经满足的条件。

代码模板如下（解析在注释里）：

int minimalRange(int[] A) {
final int N = A == null ? 0 : A.length;
int left = -1;
int ans = A.length + 1;
for (int i = 0; i < N; i++) {
while (区间超出/满足条件) {
      ans = Math.min(ans, i - left);
    }
  }
return ans;
}

注意，这里需要与最长区间的代码模板进行对比。两者的差异部分在于里面的 while 循环处理逻辑不同。在最短区间求解时，当满足条件的时候，仍然需要在这个 while 里面进行处理。

比如我们仍然以数组 [1, 2, 0, 0, 1, 2, 3] 寻找等于 6 的最短子串为例，如下图所示：

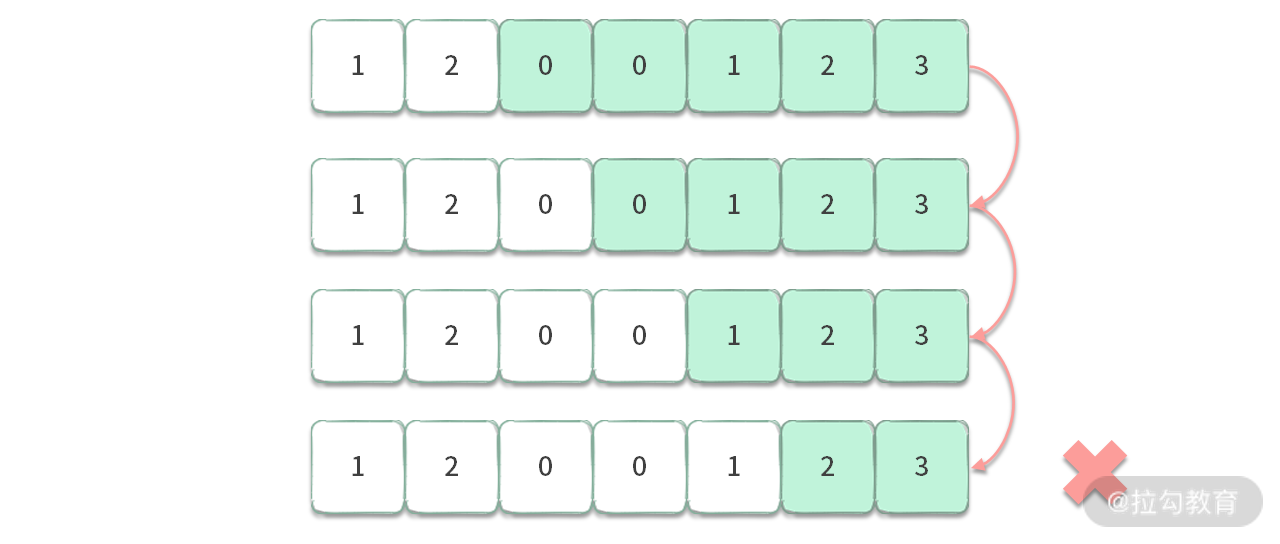
当找到一个满足条件的解之后，我们开始不停地查看更短的子串，看看有没有更好的解，并且不停地更新最优解。最终可以得到最优解：长度为 3 的子串 [1, 2, 3]。

例 5：最短子串

【题目】求 A 字符串中的最短子串，要能够包含 B 字符串中的所有字符。

输入：A = “AXCDEFCFCB”, B = “CBC”

输出：4

解释：因为 A 字符串有子串 “CFCB”，包含了 B 字符串的所有字符 “CBC”。

【分析】不知道你还有没有印象，“第 09 讲” 中讲解关于二分搜索的练习题 5 时，我们也提到了这道题。不过现在我们要尝试使用复杂度更低的双指针来解决它。首先我们来看题目的特点。

• 最短区间：题目要求一个最短的字符串。
• 约束条件：这个子串里面包含了 B 字符串的所有字符。
• 单调性：当区间变长时，包含的字符只会增加。

如果用哈希表（也可以用数组）来记录 B 字符串中字符出现的次数，也同样用哈希表来记录 A 的子串中各个字符出现的次数。那么我们还需要面临的一个问题就是如何高效地比较两个哈希是否相等。

不过好在例 3 中我们已经学会了这一招，到这里就可以开始着手写代码了。

【代码】利用最短区间的代码模板以及判断哈希表相等的思路。我们可以写出代码如下（解析在注释里）：

String minWindow(String A, String B) {
final int alen = A == null ? 0 : A.length();
final int blen = B == null ? 0 : B.length();
int[] bstat = new int[256];
int items = 0;
for (int i = 0; i < blen; i++) {
    bstat[B.charAt(i)]++;
if (bstat[B.charAt(i)] == 1) {
      items++;
    }
  }
int left = -1;
int ans = alen + 1;
int start = 0;
int[] astat = new int[256];
int equal = 0;
for (int i = 0; i < alen; i++) {
    astat[A.charAt(i)]++;
if (astat[A.charAt(i)] == bstat[A.charAt(i)]) {
      equal++;
    }
while (equal >= items) {
if (ans > i - left) {
        start = left + 1;
        ans = i - left;
      }
      ++left;
if (astat[A.charAt(left)] == bstat[A.charAt(left)]) {
        equal--;
      }
      astat[A.charAt(left)]--;
    }
  }
return ans <= alen ? 
    A.substring(start, start + ans) : new String("");
}

代码：Java/C++/Python

复杂度分析：时间复杂度 O(N)，空间复杂度 O(1)，两个 256 长度的数组，可以认为是常量空间。

【小结】到这里，我们可以总结一下这个题目的考点：

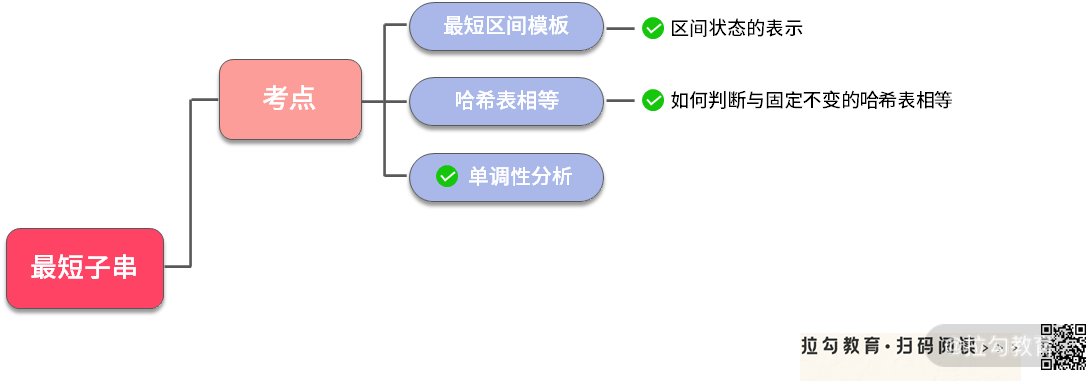
如果你能够在面试中清晰地理顺这三个考点，那么写出代码就不成问题了。

接下来我们看一个更加简单一点的练习题。

练习题 8：给定一个正整数数组 A，求一个最短子串，其和大于等于正整数 T。

代码：Java/C++/Python

总结

在这一讲里面我们介绍了三种区间的解法，以及相应的模板，基本上覆盖了绝大部分双指针算法题。我们将这部分知识点做个简单的小结，如下图所示：

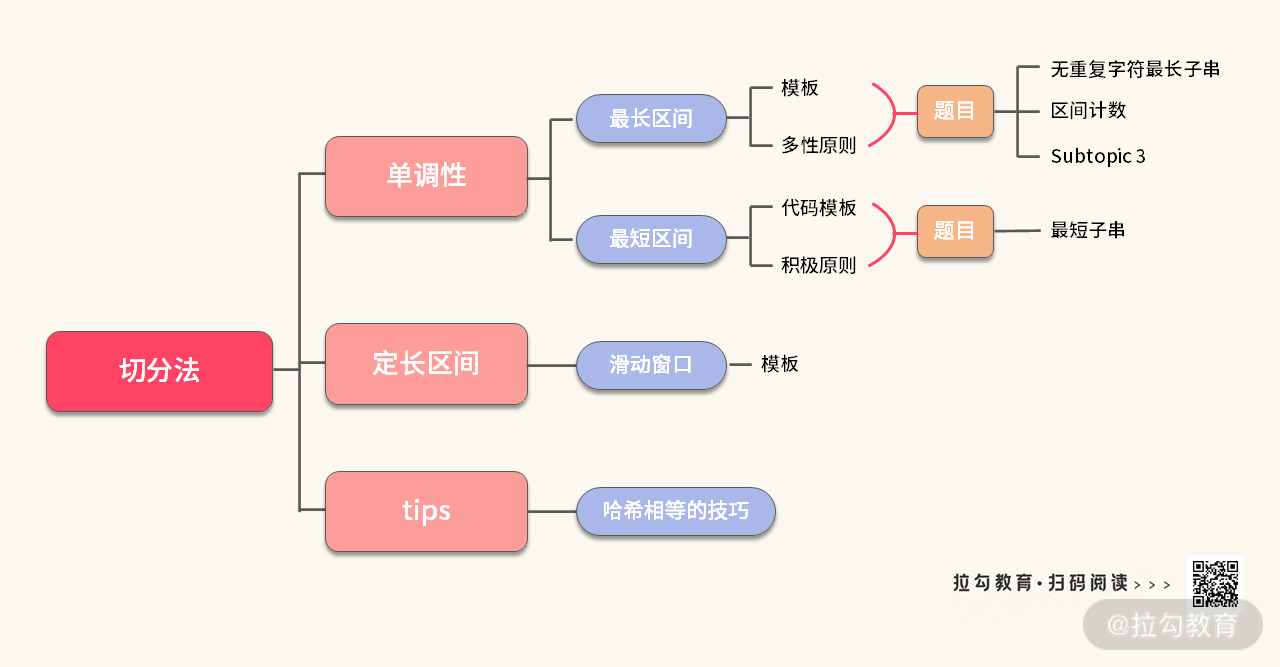
思考题

这里我给你再留一道思考题：在 “第 09 讲” 中，我们可以利用二分搜索的办法解决一些最长子串、最短子串的题目。其根本原因是什么？练习题 6 不能使用双指针模板，那么二分搜索可以吗？

希望你可以把思考写在留言区，我们一起讨论，如果看到有趣的想法，我也会做成加餐和大家分享。：）

关于双指针的知识我们就学到这里，并且有相应的代码模板。可是，并不是所有的问题都有模板可以套用的，接下来我们进入没有代码模板的算法类型。11｜贪心：这种思想，没有模板，如何才能掌握它？请和我一起踏上更加奇妙的算法旅程，记得按时来探险。