彩蛋 | 聊聊我的大厂面试经历，谈谈我对算法学习的看法

数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育

今天我想和你聊聊我的大厂面试经历，谈谈我对算法学习的看法。

我会分成三个阶段向你介绍。

• 面试前：如何准备面试。
• 面试中：面试 / 笔试中的注意事项。
• 面试后：如何回答问题与提问题。

就职现公司之前，我用一个月的时间通关了 10+ 家公司，顺利地拿下了腾讯、头条、蚂蚁、美团、eBay、微软等大厂的 Offer。

借着这个机会，我也把自己总结的 “面经” 分享给你。希望能够助力你早日拿下梦想中的职位。

面试前的准备

如果把面试比作打仗，那么在出发前我们需要确定的两件事。

• “粮草”：需要储备什么样的 “知识” 才能去面试？以及如何准备？
• “对手”：职位要求是什么？公司是做什么的？他们的业务有哪些特点？

知识的储备

一般而言，我们会把需要准备的知识分为 3 块：

• 项目经历
• 基础知识
• 算法与数据结构

这里，我首先需要重点提出来的是 “项目” 上的准备。根据我多年的面试经验，很多候选人并没有认真地准备这一块。所以，我认为有必要说一下具体应该如何准备。

面试的时候，一般开头都会问你的项目经历，有些公司甚至在面试中的某一轮只涉及项目相关的知识，完全不涉及写题。所以，你的 “项目经历” 准备得是否充分有时候也会直接影响面试结果。

1. 项目经历 5 步法

一般而言，只要介绍两段项目经历就够了。然后，针对这两个项目，你需要回答以下 5 个问题：

• 为什么会有这个项目？
• 为什么这样设计？
• 你在项目里面的角色是什么？你做了什么？
• 项目中有什么特别困难（出彩 / 你做得最好）的地方？你是如何克服的？
• 你在项目中的收获是什么？

针对这 5 个问题，你的答案需要满足以下三个特点。

• 清晰流畅：平时有空闲时间，一定要像批改作文一样，批改自己准备的答案。
• 突出重点：不要介绍无关紧要的内容，面试的每一分钟都是展示你的机会，不要浪费。
• 自我提问：在一些关键的细节上要做到非常清楚，想象一下面试官可能会提出哪些问题。
  2. 基础知识

基础知识的准备，需要根据以下 3 方面展开。

• 项目经历：有的基础知识会直接从项目经历展开，比如数据库开发，那么大概率会问到 B+ 树。
• 职位性质：比如，如果你面试的是微服务，那么关于服务治理的基础知识就需要多记忆一下。
• 公司特点：有的公司对于过往的经历和项目并不是特别看重，那么他们对基础知识的考察就会相对多一些，比如操作系统、计算机网络等。

我个人的准备顺序是：项目经历、职位性质、公司特点，优先级由高到低。

3. 算法与数据结构

算法与数据结构的准备，时间上我一般分为三个阶段。

• 重点准备的知识点
• 刷题与整理模板
• 模板复习与重点题目突击

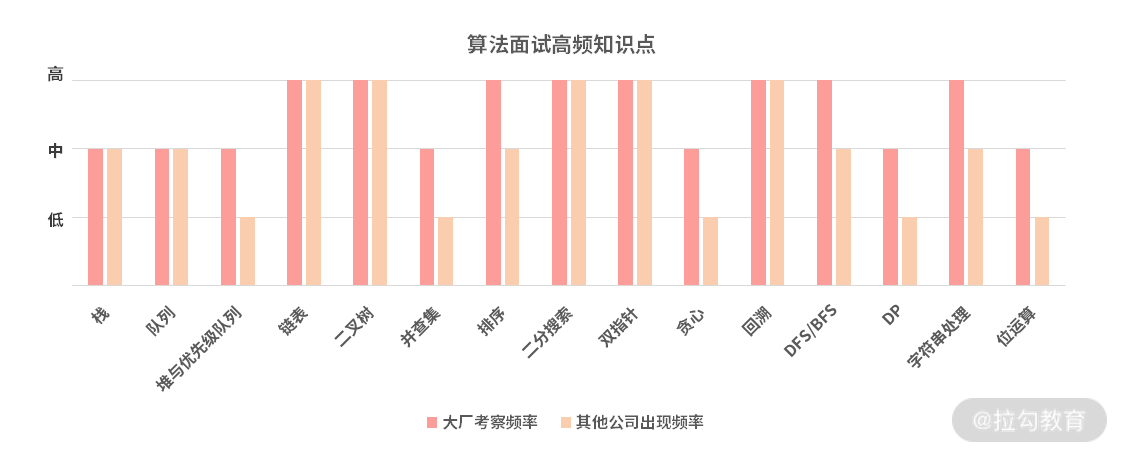
重点知识点：算法与数据结构的面试，并不需要准备到算法竞赛的程度。下图是我整理的面试常考知识点：

刷题与模板：刷题的时候，需要注意：

• 按照 tag 刷；
• 刷题的难度应该集中在中等难度；
• 按照 “一解多题” 的方式整理好知识点与模板。

这一阶段刷题结束之后，你的产出就是像《22 | 数据结构模板：如何让解题变成搭积木？》《23 | 算法模板：如何让高频算法考点秒变默写题？》给出的思维导图和代码模板。

复习与突击：主要分为模板与题目。你需要对模板代码中的思路，涉及的代码和细节都非常熟悉。

重点题目：我们应该按照 “一题多解” 的方式来过一遍重点题目，比如那些具有代表性的题目，并且在求解的时候，尽量使用我们整理过的模板。

面试现场

接下来，介绍一下我在各个大厂的面试经历，以及前面部分没有介绍过的题目。

注：涉及的公司名称我均用随机的大写字母来表示。

X 公司：第一轮

第一轮，在聊过各种项目细节之后。便打开了某客的平台开始算法笔试。余下的时间大概只有 20 分钟。

面试官：“现在我们开始写一个算法题吧。题目是这样，我给你一个树的前序和中序遍历，你能把这棵树给恢复出来吗？”

我：“请问一下，这个树是二叉树吗？二叉树里面会有重复元素吗？”

点评：给出题目之后，不要马上开始写代码，一定要与面试官沟通题意，可以当成在与客户进行沟通！因为这里的题意实际上非常含糊，没有说清楚是什么树，也没有说清楚是否有重复元素。一定不要马上往你刷过的题上去套路面试官。

面试官：“是二叉树，并且保证二叉树里面没有重复的元素！”

我：“那给定的前序遍历和中序遍历是数组吗？给定的输入是合法的吧，我不需要去处理非法的情况吧。”

面试官：“是的。我们假定给你的输入肯定都是可以恢复出一棵二叉树的。”

我：“好的，那我写一个接口给你看一下。”

于是根据面试官的要求，我写出了二叉树结点的定义：

class TreeNode {
int val = 0;
  TreeNode *left = null;
  TreeNode *right = null;
  TreeNode() {}
  TreeNode(int x) { val = x; }
}

以及接口的定义：

TreeNode buildTree(int[] preorder, int[] inorder);

接下来，我并没有立马开始写代码，而是马上与面试官过了一个简单的 Case，确保我对题意的理解是准确的。

我：“如果输入 preorder = [1, 2, 3], inorder = [2, 1, 3]。那么返回的树的结构是根结点为 1，左子结点是 2，右子结点为 3。对吗？所以这棵二叉树可以不是二叉搜索树吧？”

面试官：“是的，开始写吧。”

下面和你分享一下我的解题的思路。

• 前序遍历：根结点，左子树的所有结点，右子树的所有结点。
• 中序遍历：左子树的所有结点，根结点，右子树的所有结点。

那么，首先我可以通过前序遍历拿到根结点，然后在中序遍历中找到根结点，就可以将两个数组成功切分成三部分，如下图所示：

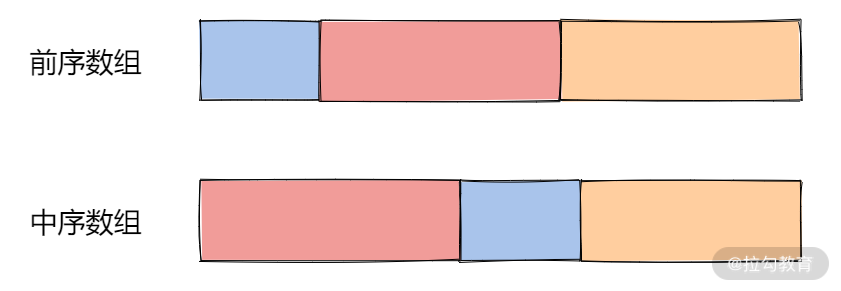
切分成三部分之后，我们可以再分别用相应的子数组构建子树。因此，整个问题遍历是类似于个递归 + 二叉树的前序遍历。

于是我开始写出第一份代码（我在真实面试中并没有写代码注释，写在这里是为了方便你查看)：

TreeNode createTree(int[] preorder, int b, int e,
int[] inorder, int f, int t) {
if (b >= e) {
return null;
  }
if (b + 1 == e) {
return new TreeNode(preorder[b]);
  }
final int rootValue = preorder[b];
final int rootPos = findPos(inorder, f, t, rootValue);
  TreeNode root = new TreeNode(rootValue);
final int leftLen = rootPos - f;
final int rightLen = t - rootPos - 1;
  root.left = createTree(preorder, b + 1, b + 1 + leftLen,
                         inorder, f, rootPos);
  root.right =
    createTree(preorder, b + 1 + leftLen, e,
               inorder, rootPos + 1, t);
return root;
}
int findPos(int[] inorder, int f, int t, int val) {
for (int i = f; i < t; i++) {
if (inorder[i] == val) {
return i;
    }
  }
return -1;
}
TreeNode buildTree(int[] preorder, int[] inorder) {
final int N = preorder == null ? 0 : preorder.length;
if (N == 0) {
return null;
  }
return createTree(preorder, 0, N, inorder, 0, N);
}

代码：Java/C++/Python

当代码写完之后，我还写了一些测试用例，如下所示：

void TEST_null() {
assert null == buildTree(null, null);
}
void TEST_length0() {
int[] preorder = new int[0];
int[] inorder = new int[0];
assert null == buildTree(preorder, inorder);
}
void TEST_single() {
int[] preorder = new int[] { 1 };
int[] inorder = new int[] { 1 };
  TreeNode ret = buildTree(preorder, inorder);
assert null != ret;
assert ret.val == 1;
assert ret.left == null;
assert ret.right == null;
}
void TEST_two() {
int[] preorder = new int[] { 1, 2 };
int[] inorder = new int[] { 1, 2 };
  TreeNode ret = buildTree(preorder, inorder);
assert null != ret;
assert 1 == ret.val;
assert 2 == ret.right.val;
}

点评：写完代码之后，不要立马交卷，好好写一些测试还是非常有必要的！

面试官看了一下代码，说：“那你这个时间复杂度是多少呢？”

我开始仔细地盘算，首先这段代码实际上是需要把数组切分为三部分，这段代码和我们学过的 “三路切分” 快排是非常类似的，那么时间复杂度应该是 O(NlgN)，其中 N 表示数组的长度。

然后我再想最差的情况。比如，如果二叉树是如下图所示的一种结构：

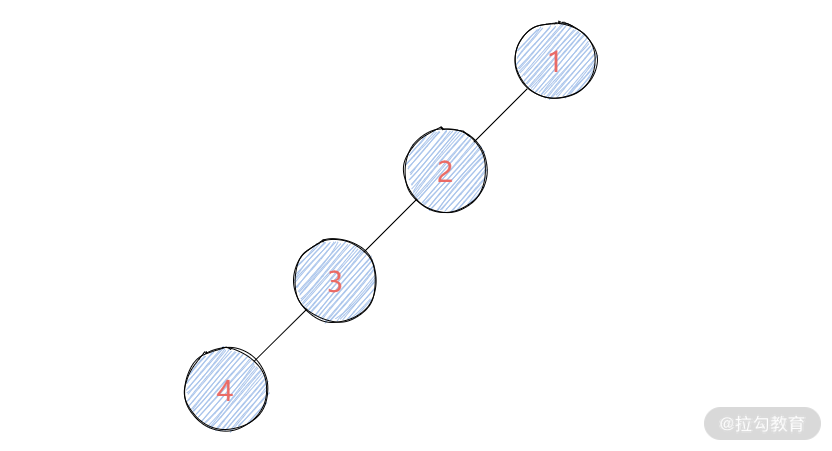
那么，preorder = [1, 2, 3, 4]; inorder = [4,3,2,1]。由于每次查找的时候都是顺序查找，那么整个时间复杂度就会达到 O(N2)。

这段代码与快排非常类似，因此，快排的时间复杂度分析就在这里用上了。

我回答面试官：“时间复杂度正常情况下是 O(NlgN)，最差会达到 O(N2)。”

面试官：“有什么优化的方法吗？”

我开始思考，首先建树的框架肯定是对的，那么时间的消耗应该就是在查找根结点的位置。我想到每个元素都不一样，是不是可以用哈希把每个元素的位置记录下来，这样就不用查找了。

我问：“可以使用哈希把每个元素在中序遍历的位置记下来，这样就可以省略掉查找的时间，那么时间复杂度就会下降到 O(N)。”

于是我又立马写了第二版代码（复制了一份，然后再修改）：

TreeNode createTree(int[] preorder,
int b,
int e,
int[] inorder,
int f,
int t,
           Map<Integer, Integer> indexHash) {
if (b >= e) {
return null;
  }
if (b + 1 == e) {
return new TreeNode(preorder[b]);
  }
final int rootValue = preorder[b];
final int rootPos = indexHash.get(rootValue);
  TreeNode root = new TreeNode(rootValue);
final int leftLen = rootPos - f;
final int rightLen = t - rootPos - 1;
  root.left = createTree(
    preorder, b + 1, b + 1 + leftLen,
    inorder, f, rootPos, indexHash);
  root.right = createTree(
    preorder, b + 1 + leftLen, e,
    inorder, rootPos + 1, t, indexHash);
return root;
}
TreeNode buildTree(int[] preorder, int[] inorder) {
final int N = preorder == null ? 0 : preorder.length;
if (N == 0) {
return null;
  }
  Map<Integer, Integer> indexHash = new HashMap<>();
for (int i = 0; i < N; i++) {
    indexHash.put(inorder[i], i);
  }
return createTree(preorder, 0, N, inorder, 0, N, indexHash);
}

代码：Java/C++/Python

面试官看了代码，觉得没有问题，然后又问了一个问题：“你这样写，空间复杂度是多少？”

我：“最差情况下都是 O(N)。”

面试官：“好的，代码没什么问题。你有什么问题要问我吗？”

于是我拿出我早就准备好的针对这个公司、小组以及职位的问题与面试官进行了一个简短的交流，然后通过了第一轮面试。

X 公司：第二轮

第二轮开始的时候，面试官并没有多说，确认通信正常后（因为是视频面试），不废话，立马开了一道算法题。

面试官：“我们先写一个题吧。在一个数组里面，只有一个数出现了 1 次，其他的数都出现了 2 次，请你把这个数找出来。”

1. 三路切分

我：“这个题可以使用一种三路切分的方法，另外也可以使用位运算的方法。”

面试官：“嗯，我还是第一次听说三路切分的方法，你能详细给我说一下吗？”

我：“原理大概是这样…… 代码可以这样写……”（这部分内容我们在《08 | 排序：如何利用合并与快排的小技巧，解决算法难题？》“例 4” 已经介绍过，这里不再赘述。）

2. bit 计数

面试官：“好的，那你能再说一下位运算的方法吗？”

我：“为了讲解这个原理，我首先采用这样一种方法进行操作。”

思路：一个整数一共有 32 个 bit，那么，我可以统计每个 bit 在数组中出现的次数。由于只有一个数出现了 1 次，其他的数都出现了 2 次。那么在最后的统计结果中，相应 bit 位为奇数的时候，只出现一次的数其 bit 位也必然为 1。

class Solution {
public int singleNumber(int[] nums) {
int[] bitCount = new int[32];
for (long x: nums) {
for (int i = 0; i < 32; i++) {
final long mask = (long)1 << i;
if ((x & mask) > 0) {
                    bitCount[i]++;
                }
            }
        }
long ans = 0;
for (int i = 0; i < 32; i++) {
if ((bitCount[i] & 0x01) == 1) {
                ans |= (long)1 << i;
            }
        }
return (int)ans;
    }
}

注意：应该用 long 的地方一定要用 long，否则在位移的时候容易出错。

面试官：“你这个算法的时间复杂度是多少？”

我：“如果是长度为 N 的数组，那么时间复杂度为 O(32N)，空间复杂度为 O(1)。所以可以认为是一个常量空间，线性时间复杂度的算法。”

面试官：“看起来常量的部分有点大，你有什么办法可以优化吗？”

我：“首先，可以优化 bit 位的计数，由于我们最终只是关心统计结果的奇偶性，因此，在某 bit 位的统计结果>= 2 的时候，我们可以直接减去 2。”

代码可以优化成这样：

class Solution {
public int singleNumber(int[] nums) {
int[] bitCount = new int[32];
for (long x: nums) {
for (int i = 0; i < 32; i++) {
final long mask = (long)1 << i;
if ((x & mask) > 0) {
                    bitCount[i]++;
                }
            }
for (int i = 0; i < 32; i++) {
if (bitCount[i] >= 2) {
                    bitCount[i] -= 2;
                }
            }
        }
long ans = 0;
for (int i = 0; i < 32; i++) {
if (bitCount[i] == 1) {
                ans |= (long)1 << i;
            }
        }
return (int)ans;
    }
}

3. 二进制计数

我：“当然，这还不是最终的版本。我们可以继续优化。因为每个 bit 计数之后，一旦>= 2 就会减去 2。那么每一位的计数实际上只会有 0，1 两种状态。既然只有 0， 1 两种状态，那么可以考虑使用二进制来表示这个计数结果。”

面试官：“可是这样，你怎么继续进行计数呢？”

我：“可以使用一个整数来表示 bitCount 数组。”

操作原理：我们用两个整数 one, two 来计数，含义如下：

如果我们将图片稍微旋转一下就得到了下图：

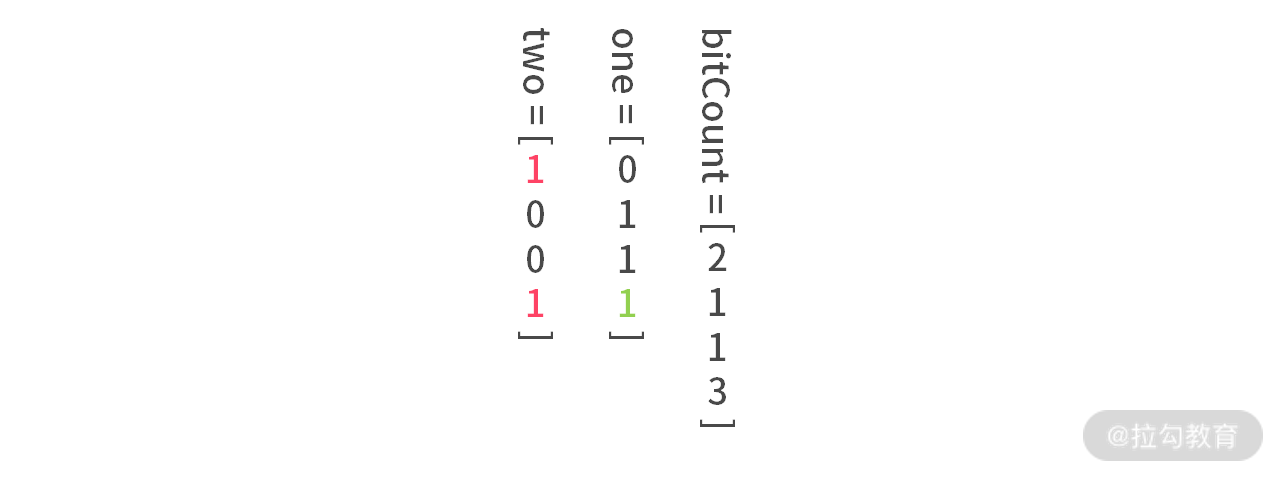
这里可以发现：

• one 表示的是每个 bitCount[] 数字的最低 bit 位；
• two 表示的是每个 bitCount[] 数字的第 2 个 bit 位。

那么，在累加的时候，我们可以采用这种办法：当 one = 0111, two = 0 的时候，bitCount[] ={0, 1, 1, 1}。假设新来一个数 x = 0b1010，那么可以得到下图：

当然，真正累加的时候，我们也不会一位一位地去加。加法采用如下方法：

int carry = one & x;
one ^= x;

那么，我们可以写出代码如下：

class Solution {
public int singleNumber(int[] nums) {
int one = 0;
int two = 0;
for (int x: nums) {
int carry = one & x;
            one ^= x;
        }
return one;
    }
}

不难发现，two 与 carry 相加的结果总是表示偶数个 bit 位。因此 two 和 carry 都可以被设置为 0。

class Solution {
public int singleNumber(int[] nums) {
int one = 0;
int two = 0;
for (int x: nums) {
int carry = one & x;
            one ^= x;
            two = 0;
            carry = 0;
        }
return one;
    }
}

我们又发现，two 和 carry 变量其实没什么用，还可以再次优化。最终版代码如下：

class Solution {
public int singleNumber(int[] nums) {
int one = 0;
for (int x: nums) {
            one ^= x;
        }
return one;
    }
}

代码：Java/C++/Python

4. 异或运算

写到这里，我又和面试官聊了另外一种思路：那就是利用异或运算的性质。

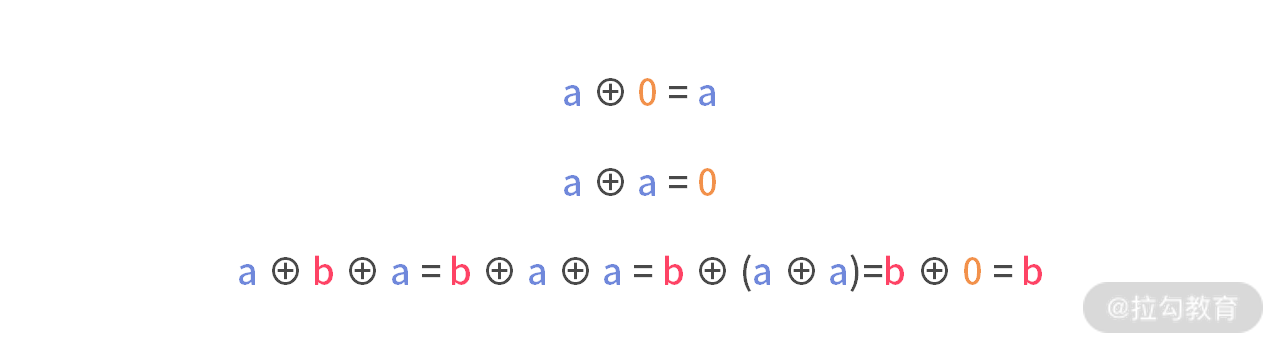
如果采用这种方法去思考，也可以得到一样的最终版的代码。

面试官：“那我们稍微把这个题目变更一下，假设除一个数字外，其他的数字都出现了 3 次。这个时候，应该怎么办？”

我：“首先，这个题目仍然可以采用” 三路切分 “的方法。”（具体可参考《08 | 排序：如何利用合并与快排的小技巧，解决算法难题？》“例 4”）。

我：“然后，这个题目还可以继续采用二进制计数的方法，当然，采用 bitCount[] 数组的方法也是可以的，但是采用异或性质的思路就不可以了。因此，三路切分和二进制计数的方法较为通用。”

面试官：“那你能写一下利用二进制的计数方法吗？我想三路切分的方法代码应该没什么变动。”

我：“好的。首先，由于除一个数字外，其他所有的数字都出现了 3 次。因此，bit 位计数的时候，>= 3 的计数都没有意义，只需要记录 0, 1, 2 三种状态。所以，我们仍然只需要两个整数 one 和 two。”

于是，延续之前的思路，可以写出如下代码：

class Solution {
public int singleNumber(int[] nums) {
int one = 0;
int two = 0;
for (int x: nums) {
int carry = one & x;
            one ^= x;
            two ^= carry;
int cnt = one & two;
            one &= ~cnt;
            two &= ~cnt;
        }
return one;
    }
}

代码：Java/C++/Python

这里我还加了一些测试代码。

5. 状态机

我：“当然，这个题还可以进一步优化。”

面试官：“我们还有一点时间，你可以简单地说一下怎么优化吗？”

优化思路：由于所有的 bit 计数都是一样的，所以我们可以把注意力放在某一个 bit 的计数上来操作（尽管一个整数有 32 个 bit，但此时我们只看一个 bit）。

由于状态是有限的（只需要记录 0, 1, 2 三种状态），那么可以采用状态机的思路来直接优化。圆圈表示某个 bit 上的计数结果，由于只有三种状态，所以我们分别用 (00, 01, 10) 来表示。那么当遇到新来的 x（带箭头的线）或为 1，或为 0 的时候，我们可以画出状态跃迁图。

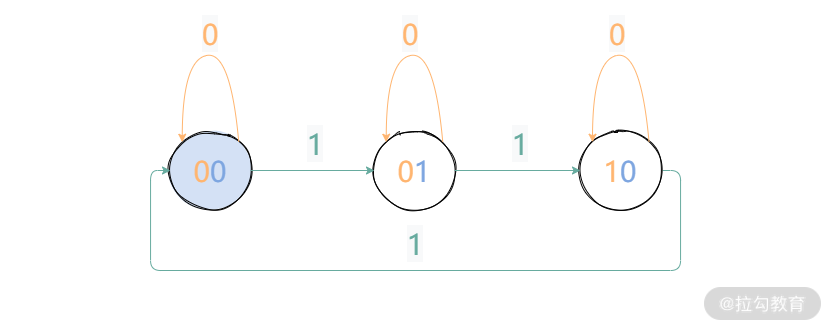
在使用二进制表示的时候，我们用 ones 表示蓝色的 bit 位。twos 表示棕色的 bit 位。那么当遇到新来的 x，我们可以整理出一个表：

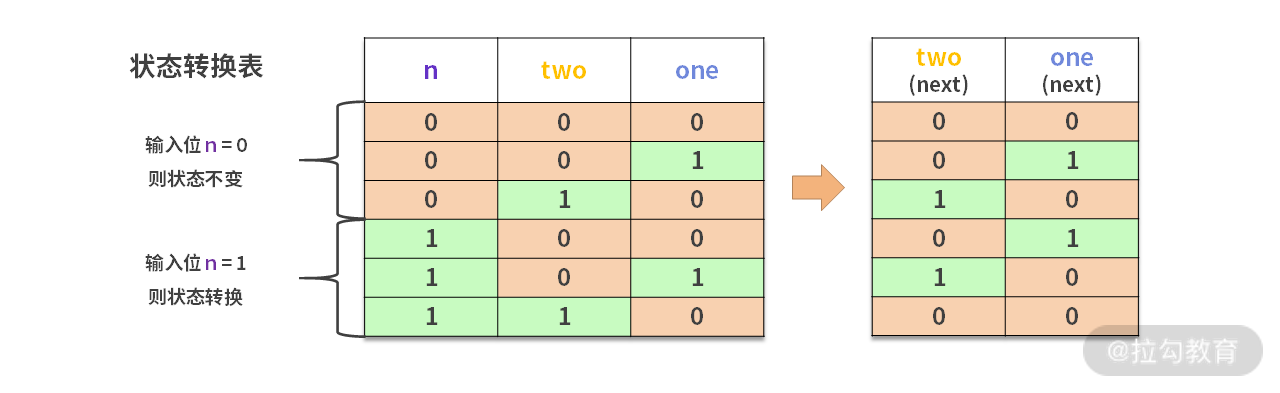
然后可以根据这个表得到化简之后的 bool 运算结果，如下图所示：

此时可以写出代码如下：

class Solution {
public int singleNumber(int[] nums) {
int ones = 0, twos = 0;
for(int num : nums){
            ones = ones ^ num & ~twos;
            twos = twos ^ num & ~ones;
        }
return ones;
    }
}

代码：Java/C++/Python
这里我还加了一些测试代码，由于篇幅原因就不进行展示了。
注意：面试遇到简单题，既是机遇，也是挑战。机遇是解题很容易，挑战则是面试官很有可能也会用同样的题目去面别人，想要出彩就需要平时多深度思考。

面试到这里，时间已经过去了一个多小时，面试官又准备问一下项目经历。这一轮时间差不多持续了两个小时以上。

Y 公司：第一轮

这次的面试是在一个茶室里面进行的，一边喝茶一边聊。从生活、工作到兴趣都聊开了。

注意：放松的面试环境非常容易让候选人放下戒备。在这种情况下，一定不要忘记深入地思考面试官提出的每个问题。

面试官看了一下表：“这样吧，我们简单写个题吧？”

我：“好啊。不过这里没有白板，我就在纸上写吧。”

注意：如果是去公司面试，最好带上电脑、纸、笔以及打印好的简历。

于是我拿出了白纸和笔，做好了准备。

面试官：“来个 24 点吧。”

我：“可以啊，就是那种我们平时玩的 24 点吧。为了简单起见，我可以直接用有效整数表示扑克的点数吗？”

面试官：“可以，我们需要把精力重点放在我们需要关注的地方。”

我：“好的，先让我整理一下思路。正常的 24 点会给 4 张卡牌，每个卡牌会用整数来进行表示。”

面试官点了点头。

我问：“那返回值返回什么呢？返回所有的解，还是返回是否有解？”

面试官：“我们先写是否有解吧。”

我：“那你看看这个接口可以吗？”

boolean judgePoint24(int[] cards)

面试官：“好的，你能说一下你的思路吗？”

我：“首先，当给定 4 个数的时候，我可以进行如下操作！”

• 从数组中挑选两个不同的数出来，此时数组中余下 2 个数。
• 尝试对这两个数进行加减乘除操作。
• 把操作的结果与余下的 12 个数放一起，构成一个新的数组，这个数组只有 3 个元素。

然后，接着处理给定输入有 3 个数的时候：

• 从数组中挑选两个不同的数出来，此时数组中余下 1 个数；
• 尝试对这两个数进行加减乘除操作；
• 把操作的结果与余下的 1 个数放一起，构成一个新的数组，这个数组只有 2 个元素。

然后，接着处理给定的输入只有 2 个数的时候：

• 从数组中挑选两个不同的数出来，此时数组中余下 0 个数；
• 尝试对这两个数进行加减乘除操作；
• 把操作的结果与余下的 0 个数放一起，构成一个新的数组，这个数组只有 1 个元素。

最后，只需要处理输入的数，如果只有一个数，那么判断这个数是否是 24 即可。

面试官：“你打算就这样写代码吗？”

我：“当然不是。由于这个过程问题规模是在不断变小的，所以我们可以使用 DFS 来求解。”

于是我先在纸上写了伪代码：

boolean judgePoint24(int[] cards) {
if cards只有一个数 and cards[0] == 24:
return true;
for x in cards:
for y in cards:
if x != y:
             ans = 利用x, y进行加/减/乘/除)
             newCards = [ans, cards.remove(x,y)]
if judgePoint24(newCards):
                 return true;
return false;
}

注意：如果你打算写伪代码，一定要给面试官明确地说明这不是最终版本的代码，而是伪代码！

面试官：“伪代码看起来没什么问题，你可以开始写了。”

我：“好。”

在纸上写代码的时候，由于涂改，容易把卷面弄得很难看。写完之后我看还有时间，就又把代码重新抄了一遍，再在另外一张纸上加了测试代码。

如果你也是在纸上写代码，那么强烈建议你重新抄一遍。因为大部分纸上手写代码都非常难看，再加上涂改，简直不能直视。

最终我交上了这么一份代码：

double[] getNextCards(double[] cards, int i, int j, double v) {
final int N = cards.length;
double[] ans = new double[N - 1];
int to = 0;
for (int k = 0; k < N; k++) {
if (k != i && k != j) {
      ans[to++] = cards[k];
    }
  }
  ans[to++] = v;
return ans;
}
boolean isResult(double value) {
if (Math.abs(value - 24.0) < 1e-6) {
return true;
  }
return false;
}
boolean notZero(double value) {
return Math.abs(value) > 1e-6;
}
boolean judge(double[] cards) {
if (cards == null) {
return false;
  }
final int N = cards.length;
if (N == 1) {
return isResult(cards[0]);
  }
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
if (judge(getNextCards(cards, i, j,
                cards[i] + cards[j])) || 
          judge(getNextCards(cards, i, j,
                cards[i] * cards[j])) || 
          notZero(cards[j]) &&
            judge(getNextCards(cards, i, j,
                  cards[i] / cards[j])) || 
          notZero(cards[i]) &&
            judge(getNextCards(cards, i, j,
                  cards[j] / cards[i])) || 
          judge(getNextCards(cards, i, j,
                cards[i] - cards[j])) || 
          judge(getNextCards(cards, i, j,
                cards[j] - cards[i]))    
      ) {
return true;
      }
    }
  }
return false;
}
boolean judgePoint24(int[] cards) {
if (cards == null) {
return false;
  }
double[] dCards = new double[cards.length];
int to = 0;
for (int x : cards) {
    dCards[to++] = x;
  }
return judge(dCards);
}

代码：Java/C++/Python

后面我还加了一系列测试代码。你在面试的时候，一定要记得主动写测试代码。

面试官：“你为什么用 isResult 和 notZero 这两个函数？”

我：“因为 double 在表示浮点数的时候，存在精度损失的情况，为了处理这两种情况，我用了 1e-6 作为边界判断两个数是否相等。”

面试官又仔细看了看代码，觉得没什么问题，然后就开始进行下一个话题的交流了。

面试的收尾

一般而言，大部分公司的算法面试结束之后，都会留一个提问环节。这里我们主要介绍这个环节需要注意地方。

提问的建议

我们的目的是求职，因此可以通过提问尽可能多地拿到关于这个职位、部门以及公司的信息。

由于大部分公司的面试都是将经理、部门负责人安排在后面。因此，这里我分享一下自己的策略（与战争进行一个类比）。

• 前两轮会侧重于当前面试的职位信息。尽量得出你在战场中的位置，你是前锋攻坚？后勤保障？还是辅助打野？
• 中间的轮次侧重于当前职位在整个部门里面的位置，能够发挥的作用，以及将要展开的项目等。得到整个部门在一场大会战中的位置，是第一梯队的部门吗？这是一个处在人员优化的部门吗？
• 后面的轮次侧重于部门在公司的位置、作用以及发展计划。公司每场 “战斗” 这个部门的参与率如何？这个部门以后还会发展吗？会独当一面成为封疆大吏吗？
• 工作节奏：如果关心工作节奏，那么也可以在技术面试中直接大方地提出来。简单直接有效地拿到一手信息。比如正常情况下的工作时间是什么样的？是否严格打卡？
• 绩效：每个公司都会有不同的方法来评定绩效。因此，我们应该认真地去拿到绩效评定的信息，这样才知道将来要努力工作的方向。

因此，提问的时候，主要是将这些信息进行整合和总结，然后得出职位的整体情况。

不建议提的问题

算法面试结束之后，我们总结一下不建议提的问题。

• 薪水：大部分时候，薪水都是由 HR 部门来决策的。无论是经理，还是技术人员，他们的作用就是根据你的面试情况进行打分。HR 会根据这个分数评定你的薪资水平。
• 结果：面试结束之后，不应该去问 “我这一轮面试过了吗？” 原因在于，大多数情况是很多人面试一个职位。公司在人员选择时，会将所有通过面试的人进行一轮排序，然后再取出 Top1, Top2 来发放 Offer。如果 Top1 拒绝，那么会给 Top2 发放 Offer。正确的心态是：好好总结，认真准备即将到来的下一场面试！
• 算法题的答案：写完题的最后环节，不应该再纠缠于前面的算法题了。你应该更多地围绕职位、部门以及公司进行提问。否则，万一通过面试入职之后，发现做的事情与心里预期不一样，岂不是很亏？
• 换组 / 换部门：一般而言，公司内部都是允许换组、换部门的。但是，应该没有一个部门会花时间帮其他部门招人，因为最好不要问这类问题。

关于面试时如何提问，如果你还有其他建议或者补充，也可以放在留言区，我们相互学习，一起讨论。

总结

在这一讲里，我们一起回顾了一段面试过程，我把这部分的内容整理在一个思维导图里方便你复习，也希望能够助力你求职成功，拿到心仪的 Offer。

此外，我还给你留了一个要特别注意的点：实事求是。如果用大白话来说就是：懂的就懂，不懂的就直接说不懂。

不要套路面试官，然后尝试一点一点往正确的答案上靠！

接下来，假设我是一个面试官，我抛出了一个问题：“给你一棵树，和两个结点，请输出这两个点的距离。”

所以这一讲留给你的作业就是：

• 你应该怎么进行沟通？
• 你应该如何写代码？
• 你应该如何写测试？

这一讲就到这里，也欢迎在留言区分享你面试经历，遇到过哪些难以解决的问题？我们一起讨论。下一讲我将和你聊一聊算法的精进之路。