03 | 优先级队列：堆与优先级队列，筛选最优元素

数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育

在电影院，相信你也看到有人持有 VIP 卡，可以直接越过队列进场去看电影。对于这种情况，我们的程序也可以用优先级队列（Priority Queue）来模拟这个场景。

通常而言，优先级队列都是基于堆（Heap）这种数据结构来实现的。因此，我们在正式开始学习优先级队列之前，还需要深入浅出地介绍一下堆及其相关的四种操作。

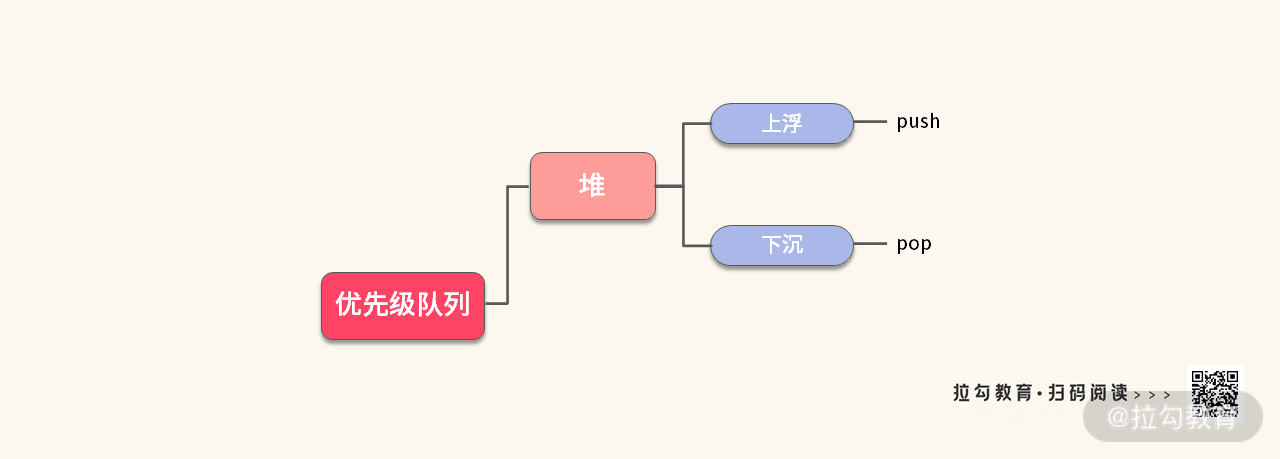
堆

FIFO 队列能够解决广度遍历、分层遍历类似的题目，FIFO 队列在遍历的时候，有一个有趣的特点：每一层结点的先后顺序，遍历时就确定下来了。

如果把这种先后顺序当成优先级，那么这些结点之间的优先级就由遍历时的顺序决定。但是有时候我们遇到的问题，结点之间需要按照大小进行排序之后，再决定优先级。在这种情况下，FIFO 队列不再适用，就需要用一种新的数据结构——优先级队列。

优先级队列底层依赖的数据结构一般是堆，而堆是面试中经常遇到的考点之一。因此，在这里我会先介绍堆的实现与要点，再介绍优先级队列的特点以及具体如何运用。

堆的分类：大堆与小堆

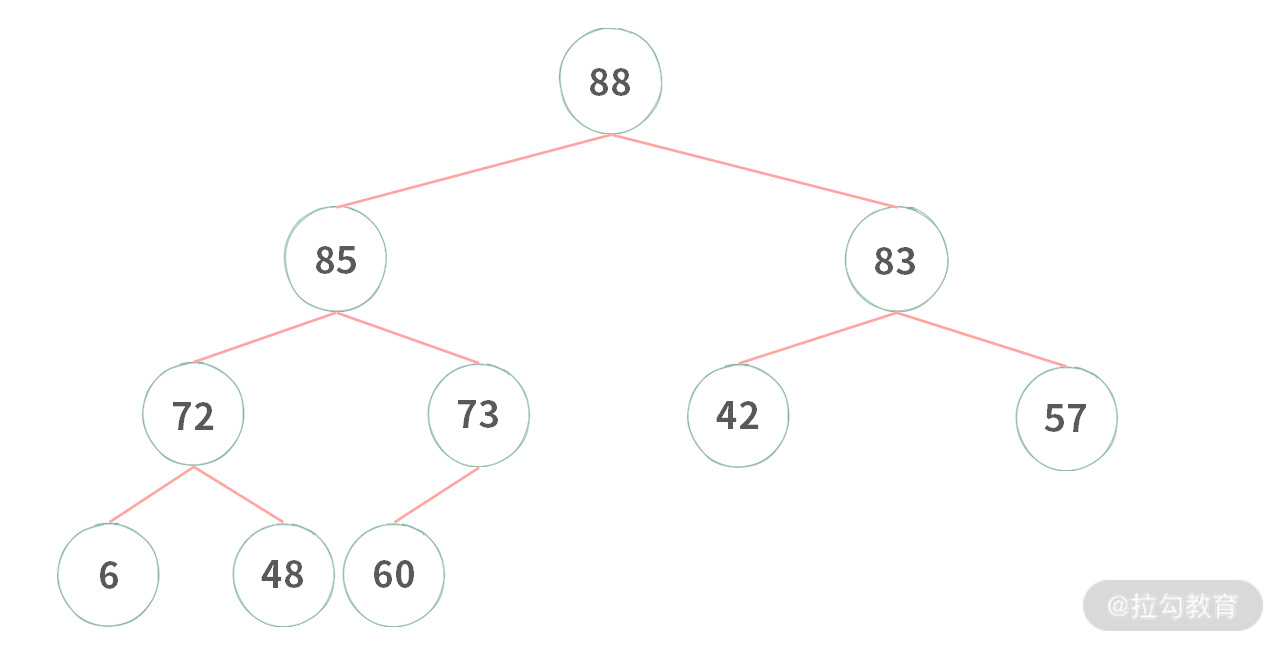
通常堆的结构都是表现为一棵树，如果根比左右子结点都大，那么称为大堆。如下图所示：

如果根比左右子结点都要小，那么称为小堆，如下图所示：

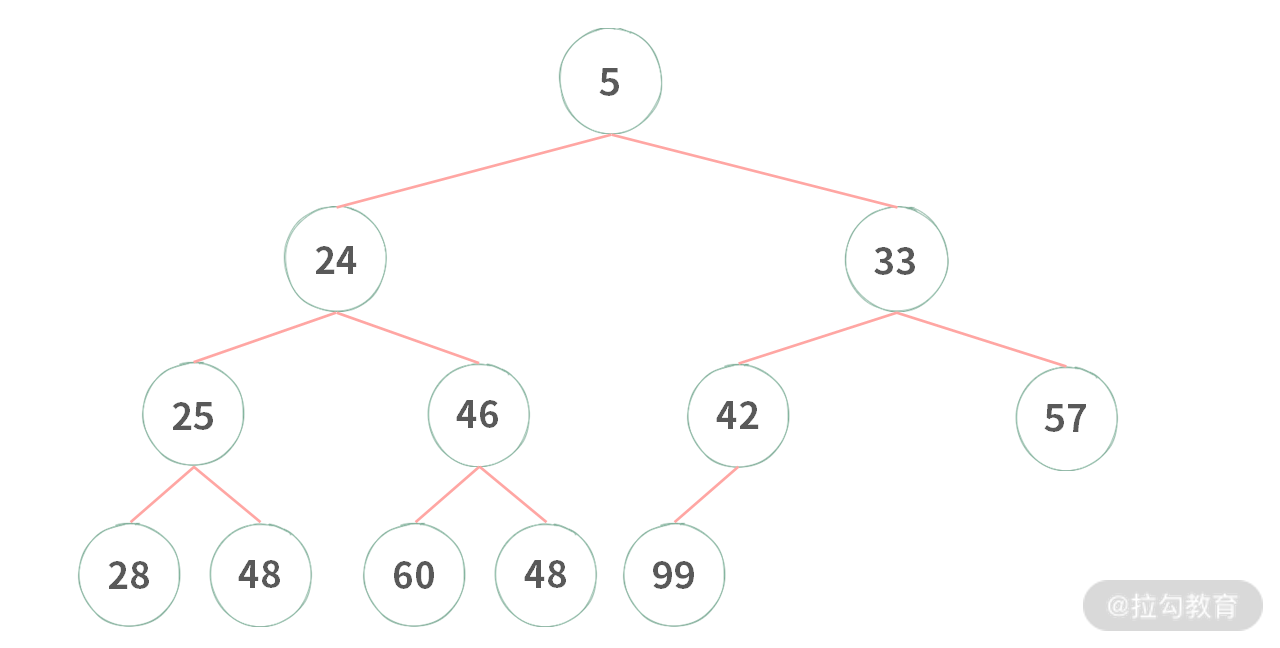
通过堆的定义，可以发现堆的特点：大堆的根是最大值，小堆的根是最小值。

更有趣的是，每次有元素 push 或者 pop 的时候，调整堆的时间复杂度为 O(lgn)，速度也非常快。因此，堆经常被用于优先级队列。接下来，我将以大堆为例，详细介绍堆的表示方式、添加元素、移除元素。

注：后面的堆操作都是基于大堆。

堆的表示

大部分时候都是使用数组表示一个堆，而不是使用二叉树。这是因为:

• 数组的内存具有连续性，访问速度更快；
• 堆结构是一棵完全二叉树。

如下图所示，堆的规律有如下几点：

• i 结点的父结点 par = (i-1)/2
• i 结点的左子结点 2 * i + 1
• i 结点的右子结点 2 * i + 2

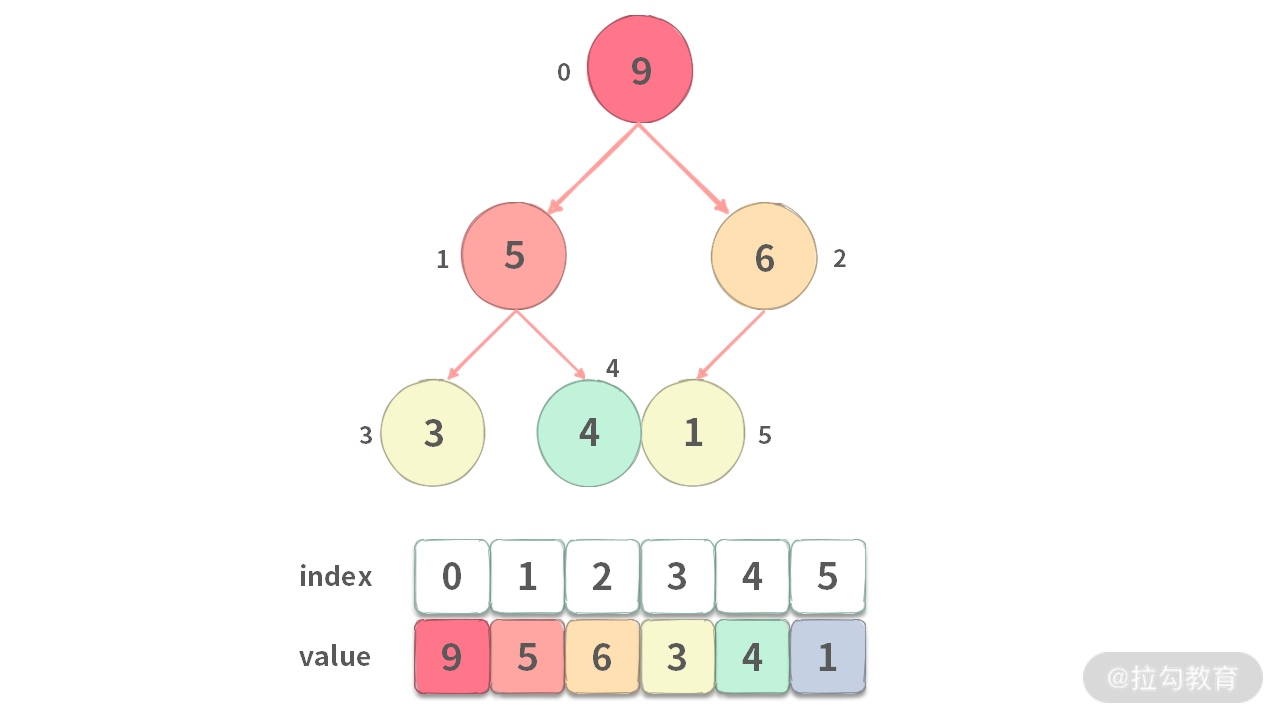
注意：这里的下标是从 0 开始的。

接下来，我们将通过具体的题目将堆的操作代码模板化。

堆的操作

堆的操作实际上只有两种：下沉和上浮，如下图所示：

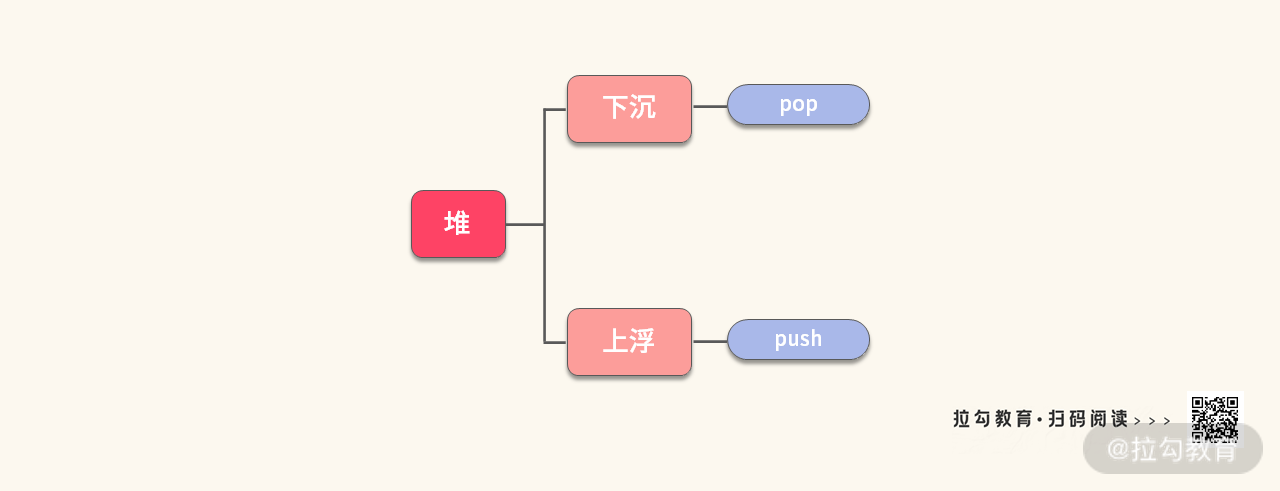
通过下沉和上浮，又可以分别得到 pop 和 push 操作，接下来我们一起讨论这四种操作的特点。

假设我们已经申请了数组 a[] 和元素 n 表示当前堆中元素的个数，代码如下：

int[] a = new int[100]; 
int n = 0;

注：这个数组的大小仅作为示例讲解，你可以根据实际情况调整，我们的重点是把算法讲清楚。

1. 下沉

引起下沉操作的原因：假设 a[i] 比它的子结点要小，那么除 a[i] 以外，其他子树都满足堆的性质。这个时候，就可以通过下沉操作，帮助 a[i] 找到正确的位置。

注意，上述操作的是大堆。

为了方便你理解，我制作了下沉过程的动图演示，如下图所示：

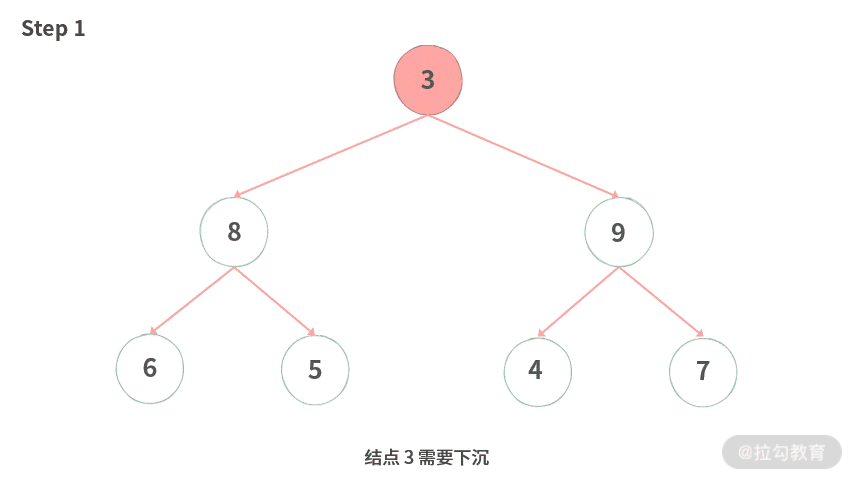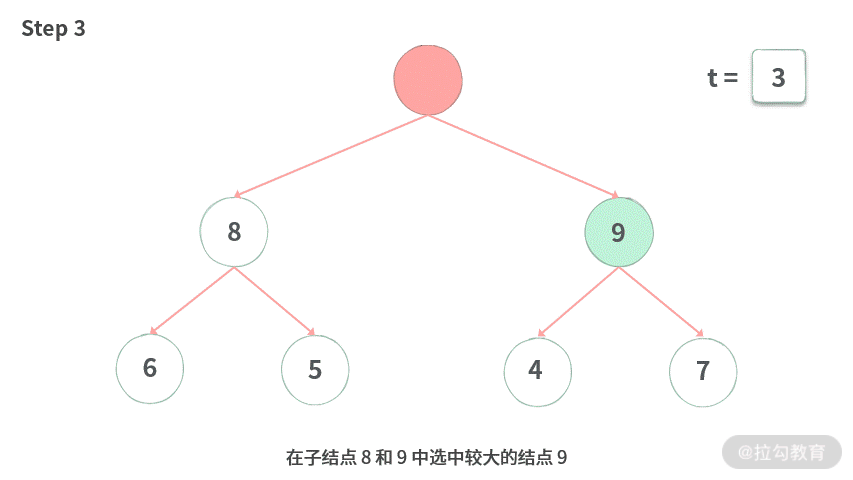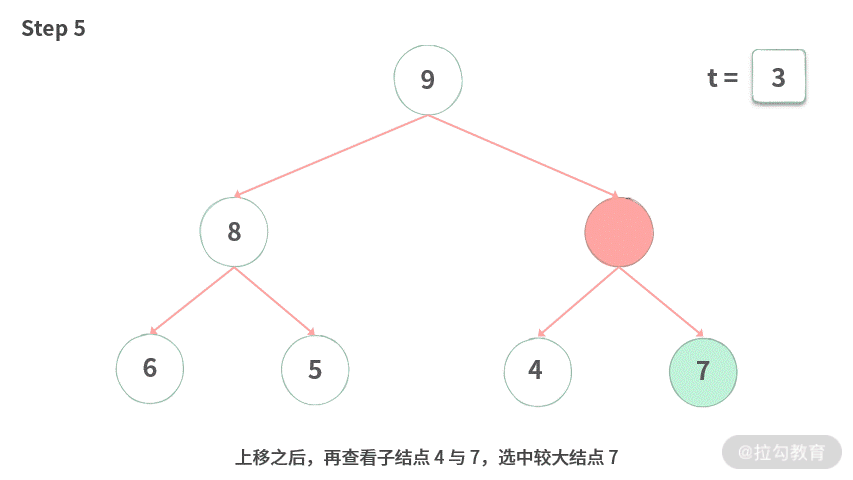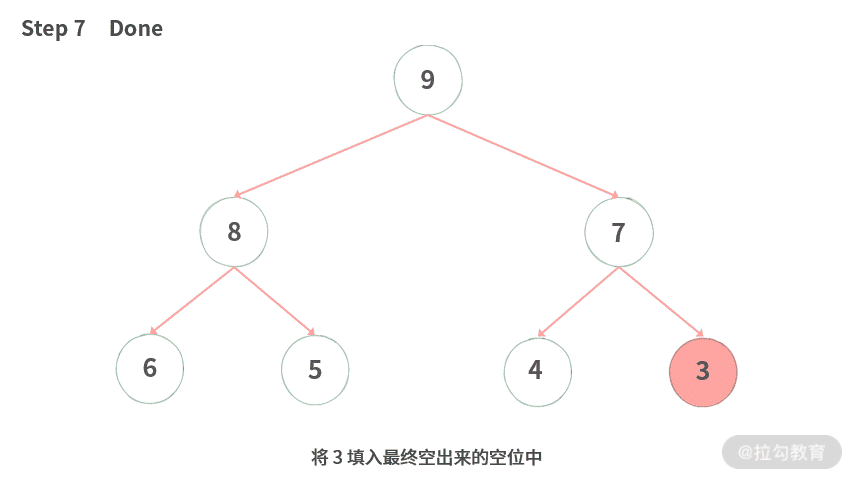
Step 1. 结点 3 需要下沉。
Step 2. 将要下沉的值存入变量 t 中，腾出空位。
Step 3. 在子结点 8 和 9 中选中较大的结点 9。
Step 4. 9 比 3 大，9 需要上移，腾出空位。
Step 5. 上移之后，再查看子结点 4 与 7，选中较大结点 7。
Step 6. 由于 7 比 3 大，7 需要上移，腾出空位。
Step 7. 将 3 填入最终空出来的空位中。

首先，写下沉代码时，需要记住一个贪心原则：如果子结点大，那么子结点就要上移。实际上，如果我们将移动路径一维化，那么这段下沉代码就会变成如下图所示的样子：

Step 1. 最大堆，结点 3 需要下沉。
Step 2. 用临时变量 t 保存值 3。
Step 3. 子结点 9 比 t = 3 大，向前移动。
Step 4. 接着子结点 7 比 t = 3 大，向前移动。
Step 5. 最终给 3 找取最终的位置。

可以发现，下沉与经典的插入排序（递减）非常相似。只有一点略有不同：插入排序是一维的，只与后继的元素进行比较，而下沉是二维的，需要在两个后继元素中找到最大值与插入值进行比较。

根据这个原则，可以写出下沉的代码如下（解析在注释里）：

private void sink(int i) {
int j = 0;
int t = a[i];
while ((j = (i << 1) + 1) < n) {
if (j < n - 1 && a[j] < a[j + 1]) {
      j++;
    }
if (a[j] > t) {
      a[i] = a[j];
      i = j;
    } else {
break;
    }
  }
  a[i] = t;
}

复杂度分析：由于堆是一个完全二叉树，所以在下沉的时候，下沉路径就是树的高度。如果堆中有 N 个元素的话，所以时间复杂度为 O(lgN)。

2. 上浮

上浮操作的条件：假设 a[i] 比它的父结点要大，并且除 a[i] 以外，其他子树都满足大堆的性质。

注意，上述操作的是大堆。

为了方便你理解，我同样制作了上浮过程的动图演示，如下图所示：

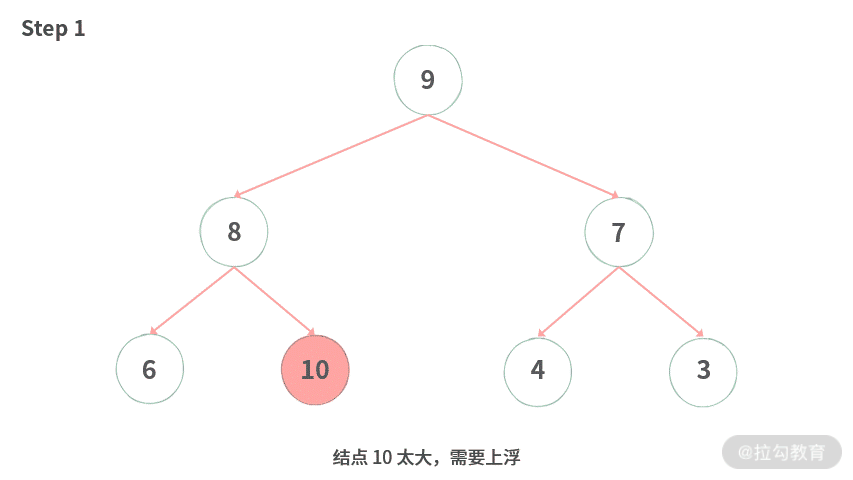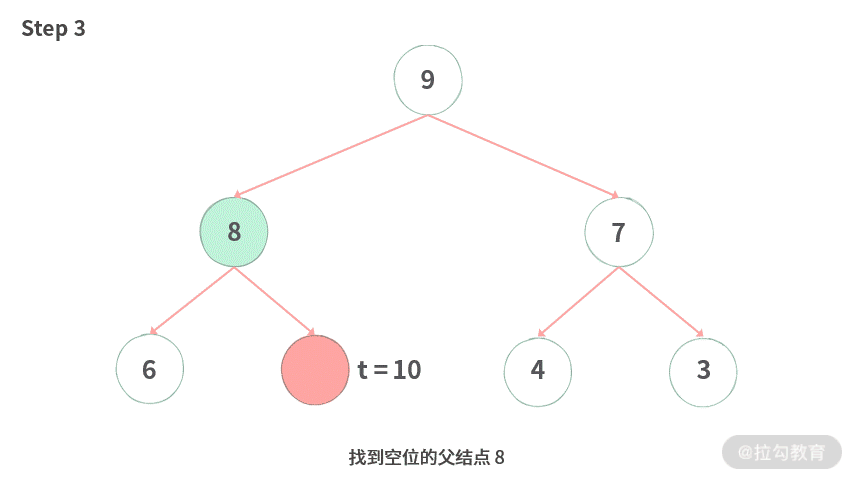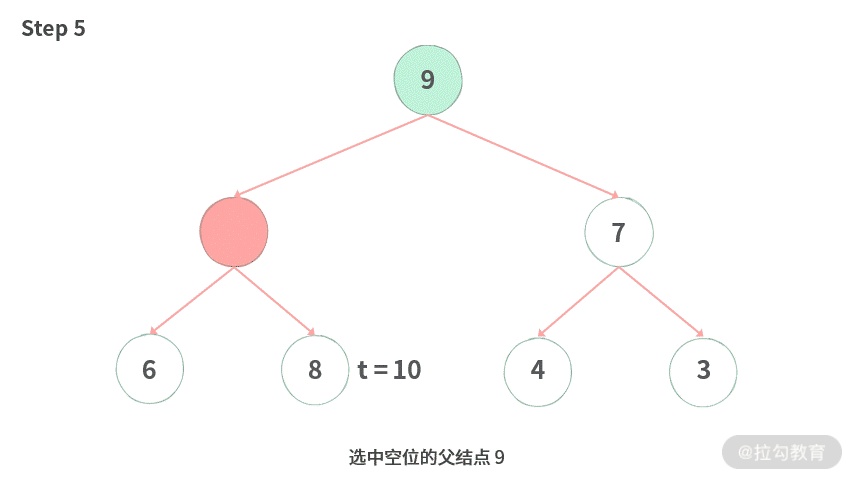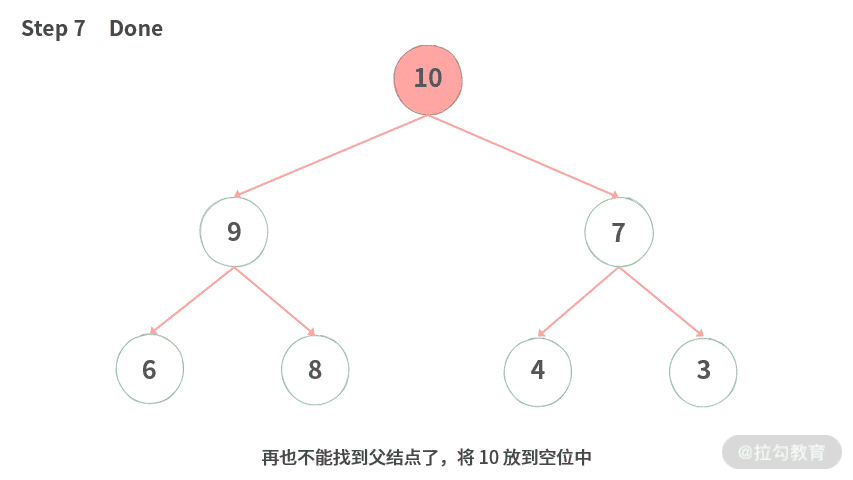
Step 1. 结点 10 太大，需要上浮。
Step 2. 将要上浮的 10 放到临时变量 t 中，腾出空位。
Step 3. 找到空位的父结点 8。
Step 4. 由于 8 比 t = 10 小，所以 8 往下移，腾出空位。
Step 5. 选中空位的父结点 9。
Step 6. 由于 9 仍然比 10 小，腾出空位。
Step 7. 再也不能找到父结点了，将 10 放到空位中。

同样，在上浮的时候，可以发现一个原则：如果父结点比 “我”小，那么父结点就需要下移。我们将移动路径一维化，这段插入代码就会变成如下图所示的样子：

Step 1. 最大堆，结点 10 需要上浮。
Step 2. 将需要上浮的 10 放到临时变量 t 中，腾出空位。
Step 3.8 比 t 小，移动 8，腾出空位。
Step 4.9 比 t 小，移动 9，腾出空位。
Step 5. 不能再移动了，将 t 放到空位中。

可以发现，上浮与经典的插入排序（递减的）非常相似。到这里，结点 a[i] 上浮的代码也比较容易搞定了。

private void swim(int i) {
int t = a[i];
int par = 0;
while (i > 0) {
    par = (i - 1) >> 1;
if (a[par] < t) {
      a[i] = a[par];
      i = par;
    } else {
break;
    }
  }
  a[i] = t;
}

复杂度分析：由于堆是一个完全二叉树，所以在上浮的时候，上浮路径就是树的高度。如果堆中有 N 个元素的话，所以时间复杂度为 O(lgN)。

3. push 操作需要两步来完成：

（1）往堆的尾巴 a[n] 上添加新来的元素

（2）新来元素 a[n] 进行上浮的操作

至此，我们可以写出代码如下（解析在注释里）：

private void push(int v) {
  a[n++] = v;
  swim(n - 1);
}

复杂度分析：主要是上浮操作，所以时间复杂度为 O(lgN)。

4. pop 操作需要以下 3 步：

（1）取出 a[0] 的值作为返回值

（2）然后将 a[n-1] 存放至 a[0]

（3）将 a[0] 进行下沉操作

有了 sink() 函数，操作还是比较简单的，我们可以直接写出代码如下：

private int pop() {
int ret = a[0];
  a[0] = a[--n];
  sink(0);
return ret;
}

复杂度分析：主要是下沉操作，所以时间复杂度为 O(lgN)。

堆的操作都梳理完成之后，这里我们给出完整的代码。虽然是一块比较基础的代码，但是我曾经在商汤的面试中就遇到过这么 “裸” 的面试题：“实现堆的 push 和 pop”。

class Heap {
private int[] a = null;
private int n = 0;
public void sink(int i) {
int j = 0;
int t = a[i];
while ((j = (i << 1) + 1) < n) {
if (j < n - 1 && a[j] < a[j + 1]) {
                j++;
            }
if (a[j] > t) {
                a[i] = a[j];
                i = j;
            } else {
break;
            }
        }
        a[i] = t;
    }
public void swim(int i) {
int t = a[i];
int par = 0;
while (i > 0 && (par = (i - 1) >> 1) != i) {
if (a[par] < t) {
                a[i] = a[par];
                i = par;
            } else {
break;
            }
        }
        a[i] = t;
    }
public void push(int v) {
        a[n++] = v;
        swim(n - 1);
    }
public int pop() {
int ret = a[0];
        a[0] = a[--n];
        sink(0);
return ret;
    }
public int size() {
return n;
    }
}

讲完了堆的四种操作，我们再来看一下如何把知识运用到题目求解和实际工作中。

例 1：最小的 k 个数

【题目】给定一个数组 a[]，返回这个数组中最小的 k 个数。

输入：A = [3,2,1], k = 2

输出：[2, 1]

【分析】这是一道来自阿里的题目。首先来看，如果是先排序，然后再返回前面的 k 个数。这样操作的复杂度是 O(nlgn)，但面试官可能想要得到复杂度更低的一些算法。

现在问题的特点是，只需要 k 个最小的数就可以了。假设我们已经拿到了前面 [0 ~ i] 个数中最小的 k 个数。那么当第 a[i+1] 进来的时候，应该怎么办呢？

接下来我们按照 “第 01讲” 介绍的 “四步分析法” 寻找解题突破口。

1. 模拟

可以采用 “挤出去的办法”：

• 先把 a[i+1] 加入集合中，此时集合中已经有 k+1 个数了；
• 再把集合 k+1 个数中的最大的数扔出去。

此时，存留下来的 k 个数，就是 [0 ~ i + 1] 里面最小的 k 个数了，具体演示如下图所示：

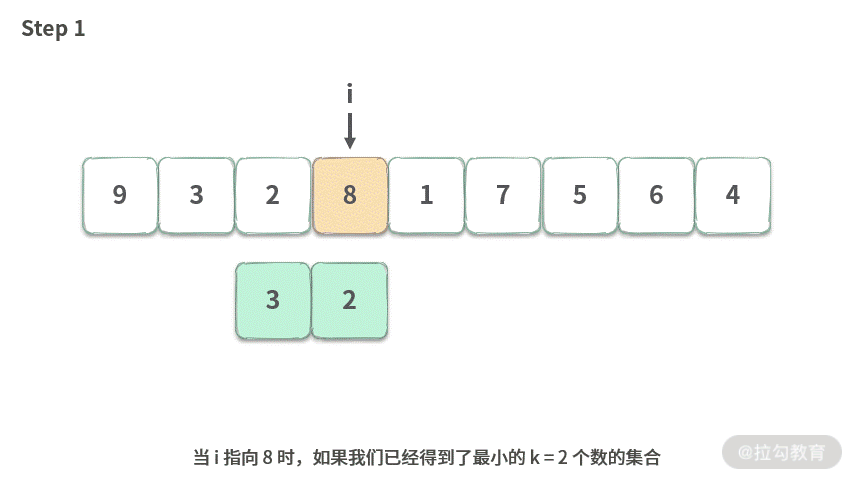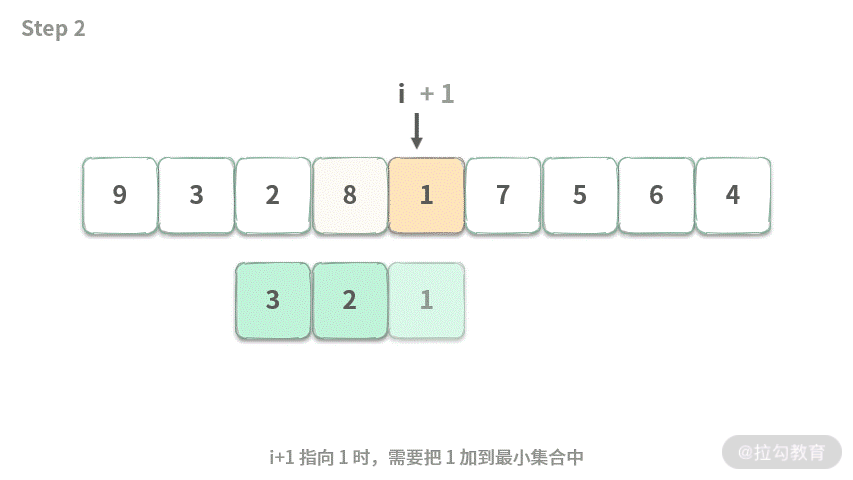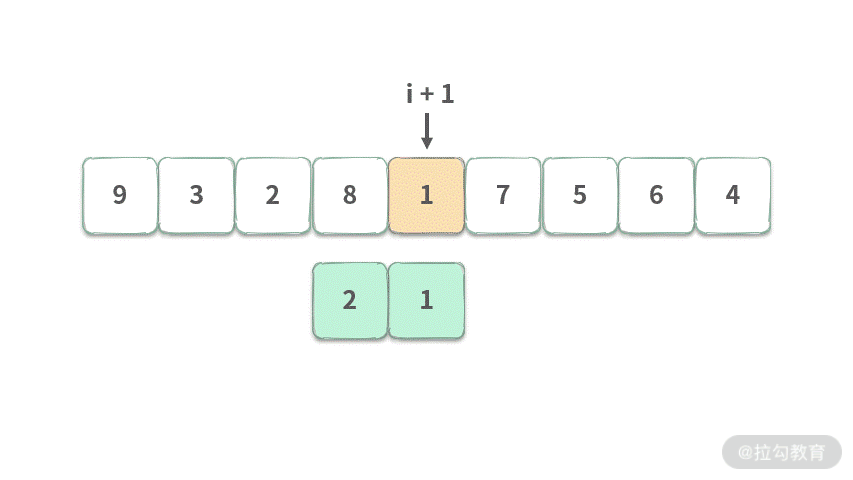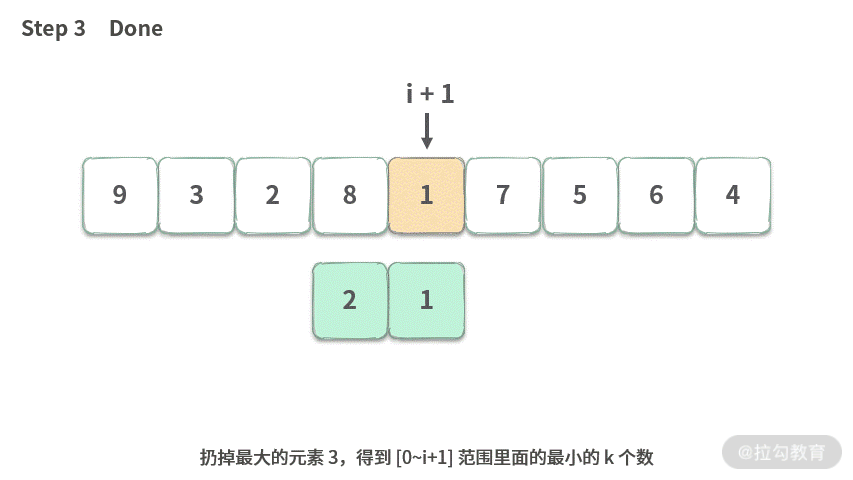
Step 1. 当 i 指向 8 时，如果我们已经得到了最小的 k = 2 个数的集合。
Step 2.i+1 指向 1 时，需要把 1 加到最小集合中。
Step 3. 扔掉最大的元素 3，得到 [0~i+1] 范围里面的最小的 k 个数。

2. 规律

由上述分析可以找出以下两个规律：

（1）我们要的是一个集合，这个集合并不需要有序，但需要支持 push 功能；

（2）pop 的时候，总是把最大的元素扔出去。

3. 匹配

基于我们发现的两个规律，可以得出，这个时候应该使用大堆。因为堆满足：

（1）内部并不是有序的，支持 push 功能；

（2）pop 时，扔掉堆里最大元素就可以了。

4. 边界

数据结构选定后，在面试时，你还需要思考一下问题的边界。给定数组和 k 的情况，应该有以下 7 种：

（1）数组为 null

（2）数组中元素个数小于 k

（3）数组中元素个数等于 k

（4）数组中元素个数大于 k

（5）k < 0

（6）k == 0

（7）k > 0

【画图】分析到这里。我们可以利用大堆完成一次模拟了，动图演示如下：

输入：[9, 3, 2, 8, 1, 7, 5, 6, 4], k = 4

输出：[1,2,3,4]

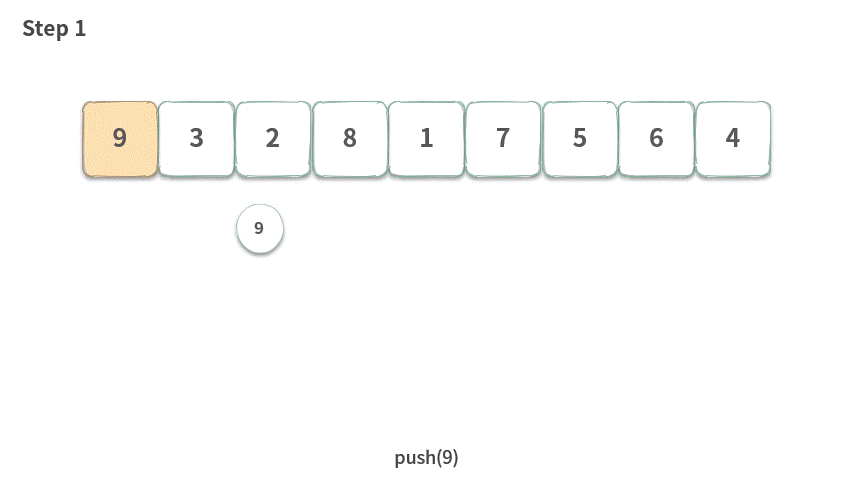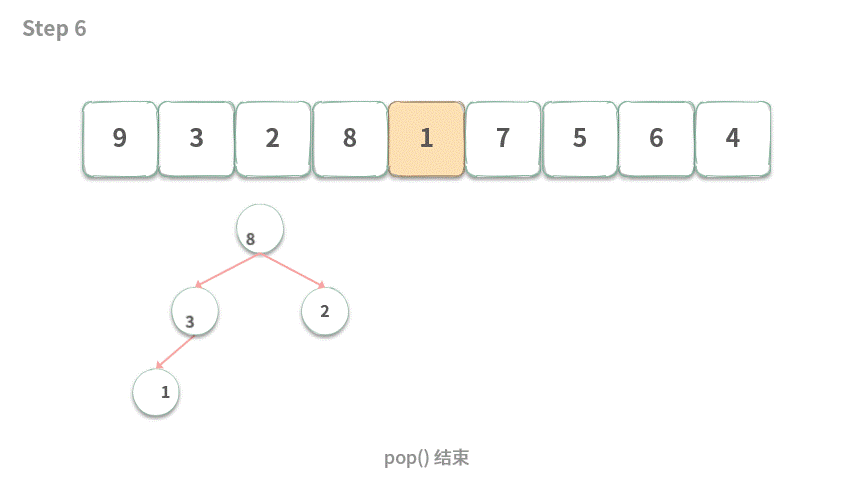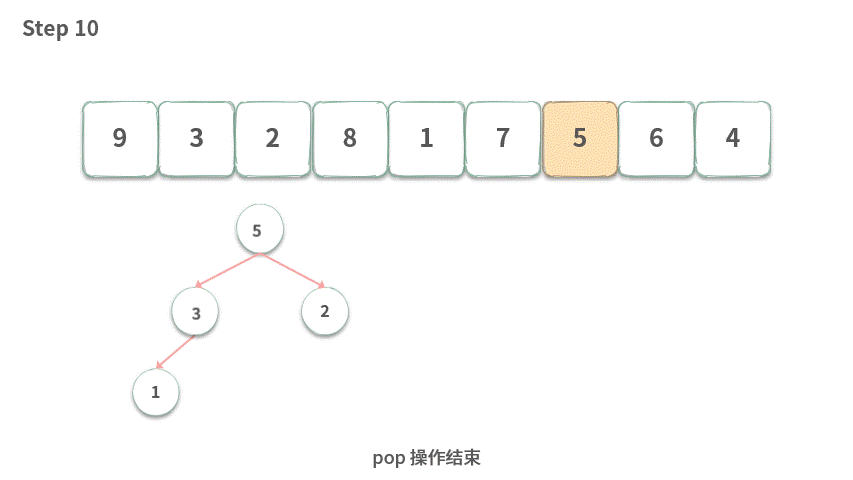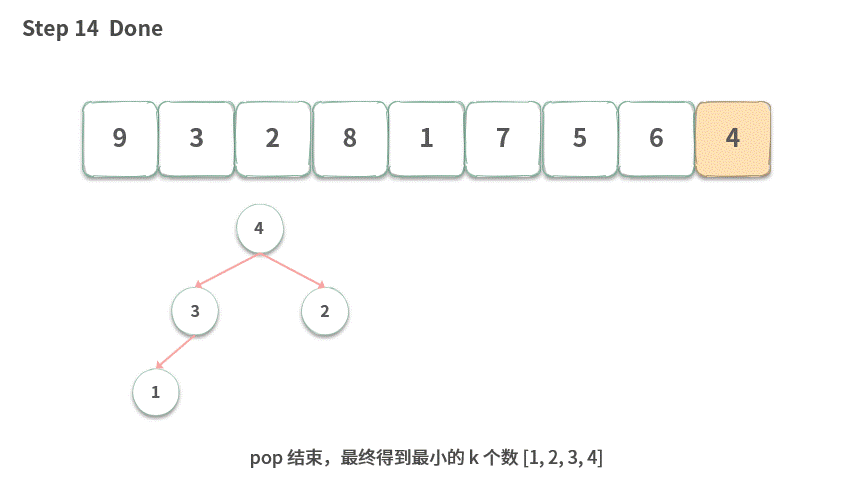
Step 1.push(9)。
Step 2.push(3)。
Step 3.push(2)。
Step 4.push(8)。
Step 5.push(1)，堆中元素个数 > k，需要执行 pop。
Step 6.pop() 结束。
Step 7.push(7)，堆中元素个数 > k，需要执行 pop。
Step 8.pop 操作结束。
Step 9.push(5)，堆中元素个数 > k，需要执行 pop。
Step 10.pop 操作结束。
Step 11.push(6)，堆中元素个数 > k，需要执行 pop。
Step 12.pop 结束。
Step 13.push(4)，堆中元素个数 > k，需要执行 pop。
Step 14.pop 结束，最终得到最小的 k 个数 [1, 2, 3, 4]。

【代码】接下来，就可以开始写代码了，也是时候亮出你真正的实力了。代码如下（解析在注释里）：

class Solution {
private int[] a = null;
private int n = 0;
private int size() {
return n;
  }
public int[] getLeastNumbers(int[] arr, int k) {
if (k <= 0 || arr == null || arr.length == 0) {
return new int[0];
    }
    a = new int[k + 1];
    n = 0;
for (int x : arr) {
      push(x);
if (size() > k) {
        pop();
      }
    }
int[] ans = new int[k];
int i = 0;
while (size() > 0) {
      ans[i++] = pop();
    }
return ans;
  }
}

代码：Java/C++/Python

复杂度分析：时间复杂度，每个元素都需要入堆，而堆 push 的时间复杂度为 O(lgk)。因为我们控制了堆的大小为 k，所以总的时间复杂度为 O(Nlgk)。因为我们使用了 k 个元素的堆，所以空间复杂度为 O(k)。

【小结】在这个并不算难的题目里，我们为了深入讲解优先级队列的原理，采用了一种 “最费劲” 的方式（自己写堆）来操作。

但实际上，大部分语言都内置了堆的实现（优先级队列）。当你面试的时候，如果面试官没有明确提出要求你自己写堆，赶紧麻溜地用内置的优先级队列啊！

接下来，我们一起看看如何用语言内置的优先级队列来解决这个问题。代码如下（解析在注释里）：

class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k <= 0 || arr == null || arr.length == 0) {
return new int[0];
        }
        Queue<Integer> Q = new PriorityQueue<>((v1, v2) -> v2 - v1);
for (int x: arr) {
            Q.offer(x);
while (Q.size() > k) {
                Q.poll();
            }
        }
int[] ans = new int[k];
int i = 0;
for (int x: Q) {
            ans[i++] = x;
        }
return ans;
    }
}

代码：Java/C++/Python

复杂度分析： 首先堆的大小为 k，那么每次 push/pop 的复杂度都是 O(lgk)。一共有 n 个元素，所以复杂度为 O(nlgk)。

此外，这道题还有不使用优先级队列，直接可以达到 O(N) 复杂度的算法，你可以尝试思考一下。

代码：Java/C++/Python
注：如果看不懂也没有关系，我们在 “第 08 讲” 介绍快排时还会进一步讲解。

关于解决这类题目的思路、重点以及分析方法，建议你先尝试自己梳理总结一下，再来看我给出的思维导图：

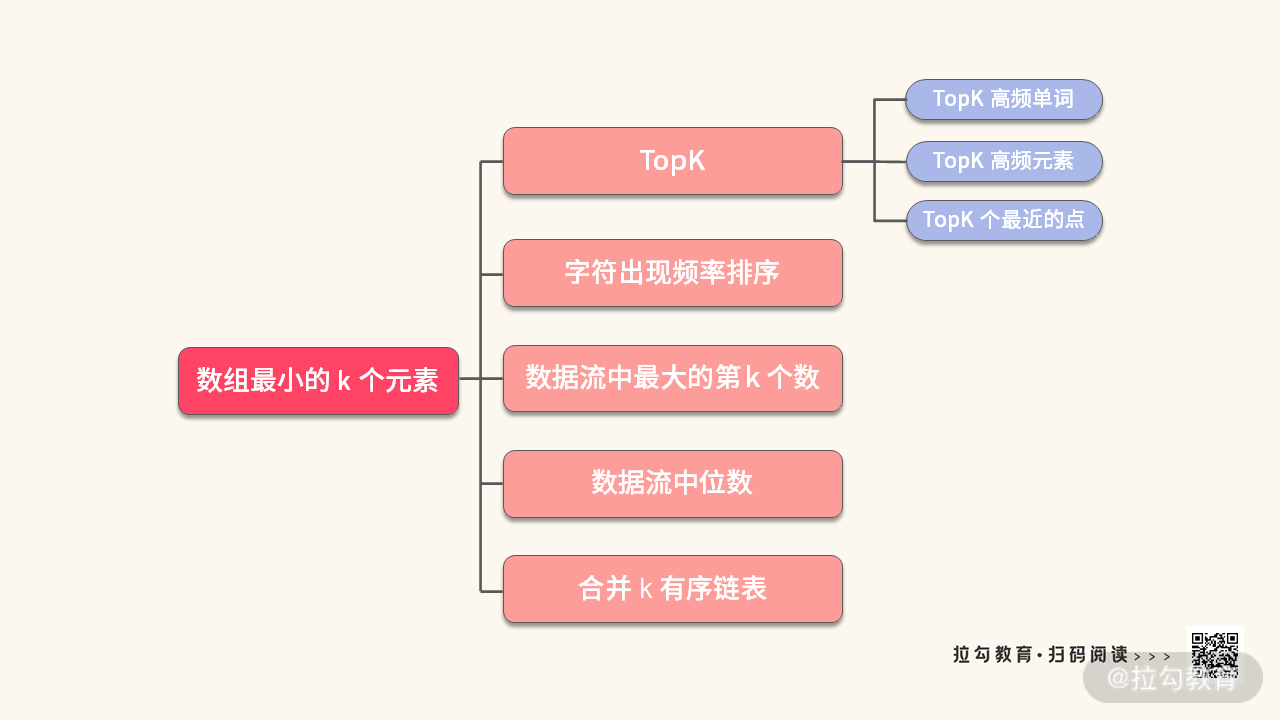
例 1 是一道非常经典的题目，如果你掌握了这道题的解题思想，可以举一反三解决更多的题目。这里我给出一些堆的练习题。

练习题 1：给定一个数组，求这个数组的前 k 个高频元素。如果有两个数出现次数一样，那么优先取较小的那个数。

输入：A = [1,2,1,1,3,3,2,3] k = 2

输出：[1, 3]

解释：每个数字的出现频率从高到低排序 <1, 3 次>, <3,3 次 > <2, 2 次 >，取前 2 个高频数字。所以是 [1, 3]。

代码：Java/C++/Python

练习题 2：在练习题 1 的基础上，给定的是一个单词数组，求这个数组前 k 个高频单词。如果有两个单词出现频率是一样的。那么输出字典序较小的那个单词。

输入：A = [“AA”, “BB”, “AA”, “BB”, “CCC”, “CCC”, “CCC”, “AA”] k = 2

输出：[“AA”, “CCC”]

解释：出现次数最多的 2 个单词就是[“AA”, “CCC”]

代码：Java/C++/Python

练习题 3：给定一个点集数组 A[]，求离原点最近的 k 个点。

输入：A = [[0,1], [1,0], [100,1], [1,100]], k = 2

输出：[[0,1], [1,0]]

解释：离原点最近的两个点就是 [[0,1], [1,0]]

代码：Java/C++/Python

练习题 4：将 k 个有序的链表，合并成一个有序的链表。

代码：Java/C++/Python

练习题 5：给定两个有序数组，两个数组中各找一个数，凑成一对，找出相加之和最小的 k 对。

输入：A = [1, 1, 2], B = [1, 2, 3], k = 2

输出：B = [[1, 1], [1, 1]]]

解释：A,B 数组中各取一个 1 出来凑成一对，其和 [1+1=2, 1+1=2]是最小的 2 对。

代码：Java/C++/Python

优先级队列

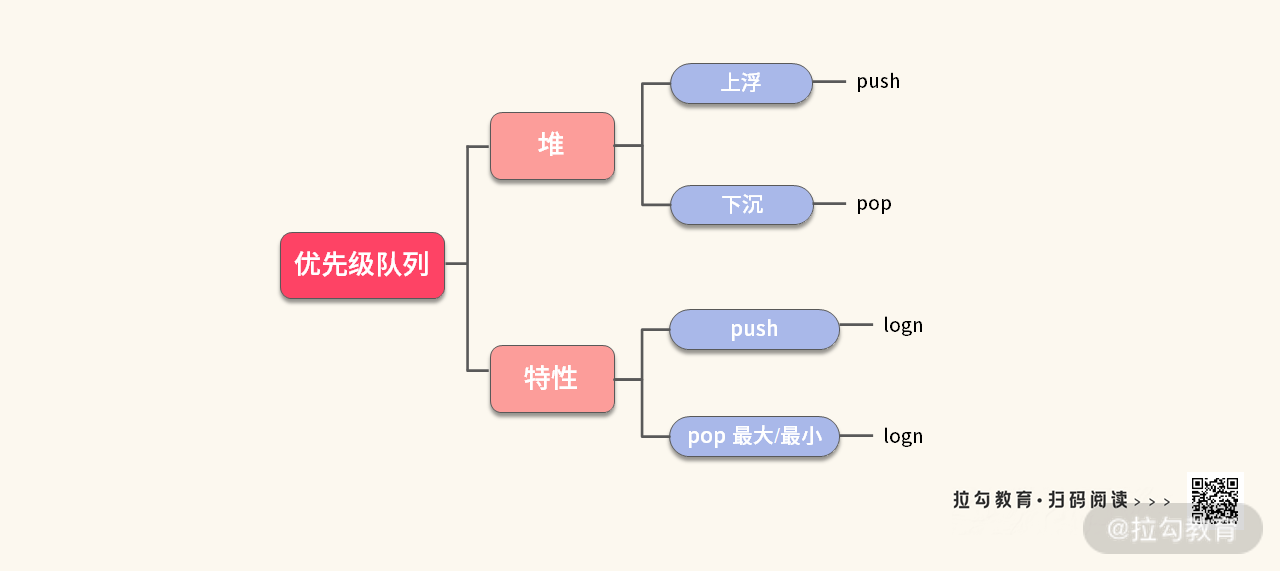
前面提到，优先级队列主要基于堆来实现，因此，堆具备的特性优先级队列也同样具备。比如：

• 可以 O(lgn) 的复杂度往优先级队列中添加元素；
• 可以 O(lgn) 的复杂度从优先级队列弹出最大 / 最小元素。

经过简化，我们可以得到优先级队列的特性，如下图所示：

不过，如果只是知道这两个特性，你还不能从容地应对面试。接下来，我们一起看一下优先级队列的深度运用。

例 2：跳跃游戏

【题目】假设你正在玩跳跃游戏，从低处往高处跳的时候，可以有两种方法。

方法一：塞砖块，但是你拥有砖块数是有限制的。为了简单起见，高度差就是你需要砖块数。

方法二：用梯子，梯子可以无视高度差（你可以认为再高也能爬上去），但是梯子的个数是有限的 (一个只能用一次)。

其他无论是平着跳，还是从高处往低处跳，不需要借助什么就可以完成（在这道题中我们默认无论从多高跳下来，也摔不死）。

给你一个数组，用来表示不同的高度。假设你总是站在 index = 0 的高度开始。那么请问，你最远能跳到哪里?

输入：[3, 1, 6, 20, 10, 20], bricks = 5, landers = 1

输出：4

解释：

• Step 1. 从 3 跳到 1 时，因为是从高往低处跳，直接跳就可以了
• Step 2. 从 1 到 6 时，用掉 5 个砖块
• Step 3. 从 6 到 20 时，用掉梯子
• Step 4. 从 20 到 10 可以直接跳
• Step 5. 到 10 这里就停住了，没有东西可以帮助你跳到 20 了，所以只能跳到下标 index = 4 这里。

【分析】这是一道来自拼多多的面试题。首先我们想一想在什么情况下使用梯子？因为梯子最好用，可以无视高度直接使用。但是这里有一个限制条件，只能在大高度差的时候使用梯子。如果是在小高度差的时候使用，那么最终就走不远，比如对于上面给定的例子：

• Step 1. 从 3 跳到 1 时，直接跳就可以了；
• Step 2. 从 1 到 6 时，用掉梯子；
• Step 3. 从 6 到 20 时，手里的 5 个砖头就不够用了！所以最远只能到下标 index = 2。

因此，我们选择使用梯子的时候，一定要使用得当！那么应该如何判断在什么情况下使用梯子呢？

下面可以尝试换种思路，从低往高跳跃的时候，本来是要使用砖块的。但是可以想象成我随身带着一个本子，在上面记录落差 (落差定义为：低往高处跳时的高度差)。比如从高度 1 跳到高度 6，就在小本子上写 5。而高处往低处跳的时候，不需要记录，因为这不是落差（题目说了高往低处跳可以直接跳，没有必要记录）。

在跳跃的时候，一定要保证小本子上的落差之和要小于等于砖块数目。可是当落差大于砖块之和时怎么办呢？

别忘了，我们还有梯子呢。梯子可是万能的（可以把梯子想象成一次性橡皮擦 ）！如果还有梯子，我们只需要从小本子上挑出最大的落差，用 “一次性橡皮擦” 将它从小本上擦掉即可。

1. 模拟

有了思路之后，我们来执行一次模拟。具体演示如下图所示：

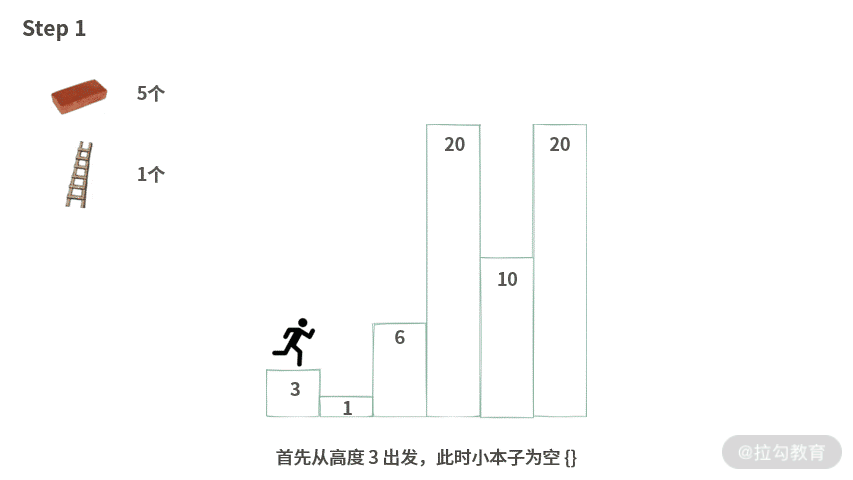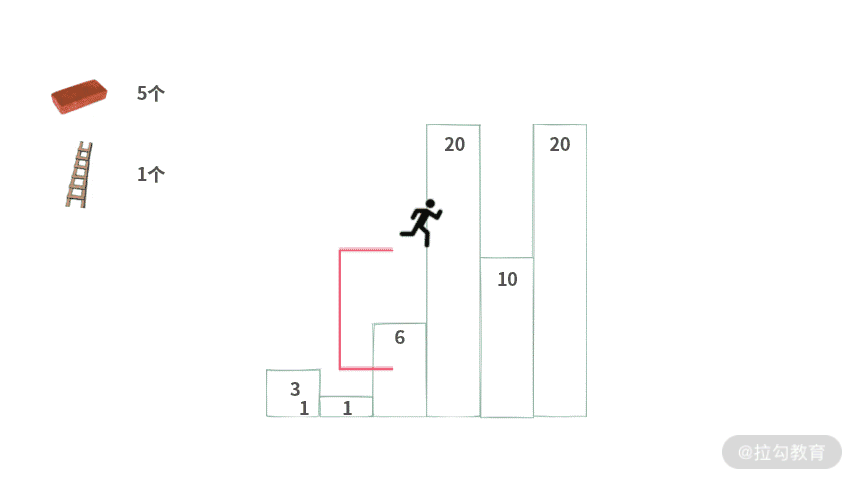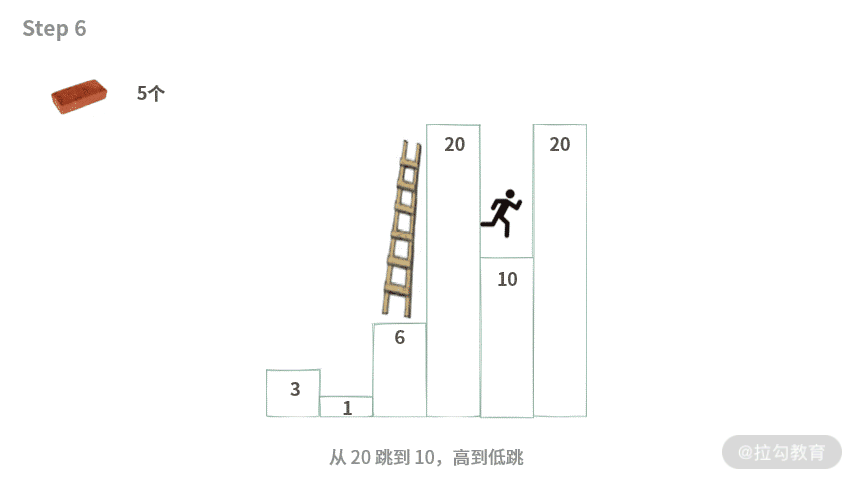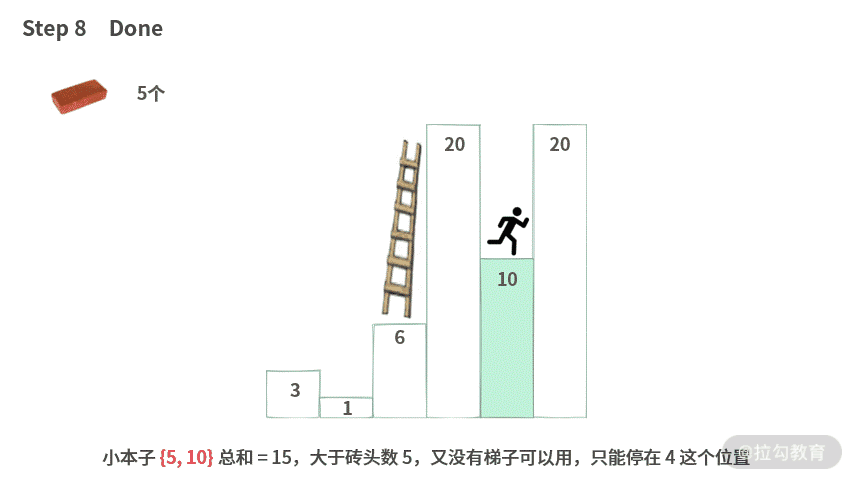
Step 1. 首先从高度 3 出发，此时小本子为空 {}。
Step 2. 从高度 3 跳到高度 1（高往低跳，无压力），此时小本子仍然为空 {}。
Step 3. 从 1 跳到高度 6，小本子记录落差 {5} <= 砖头数 5。
Step 4. 从 6 跳到 20, 小本子记录 {5, 14}，总和 > 砖头数 5。
Step 5. 需要从小本子 {5, 14} 中选出最大数 14，然后梯子替换掉。
Step 6. 从 20 跳到 10，高到低跳。
Step 7. 要从 10 跳到 20，需要把落差 10 记录到本子上 {5, 10} 。
Step 8. 小本子 {5, 10} 总和 = 15，大于砖头数 5，又没有梯子可以用了。因此只能停在 4 这个位置。

2. 规律：在这里，我们发现小本子有两个有趣的地方：

（1）需要在小本子上记录落差；

（2）需要用梯子来替换最大的落差。

在我们学过的数据结构里面，满足这个 push/pop 特点的，应该就是优先级队列啦。

3. 边界：注意考虑给定数组为空的情况。

【代码】到这里，可以开始写出代码了。具体代码如下（解析在注释里）：

class Solution {
public int furthestBuilding(int[] heights, int bricks, int ladders) {
if (heights == null || heights.length == 0) {
return -1;
        }
        Queue<Integer> Q = new PriorityQueue<>((v1, v2) -> v2 - v1);
int qSum = 0;
int lastPos = 0;
int preHeight = heights[0];
for (int i = 1; i < heights.length; i++) {
final int curHeight = heights[i];
if (preHeight >= curHeight) {
                lastPos = i;
            } else {
final int delta = curHeight - preHeight;
                Q.offer(delta);
                qSum += delta;
while (qSum > bricks && ladders > 0) {
                    qSum -= Q.peek();
                    Q.poll();
                    ladders--;
                }
if (qSum <= bricks) {
                    lastPos = i;
                } else {
break;
                }
            }
            preHeight = curHeight;
        }
return lastPos;
    }
}

代码：Java/C++/Python

复杂度分析：在跳跃的过程中，最差的情况下，我们需要把所有的高度差记录下来。在这种情况下，每个高度差都需要执行 push 操作。那么时间复杂度为 O(NlgN)，空间复杂度为 O(N)。

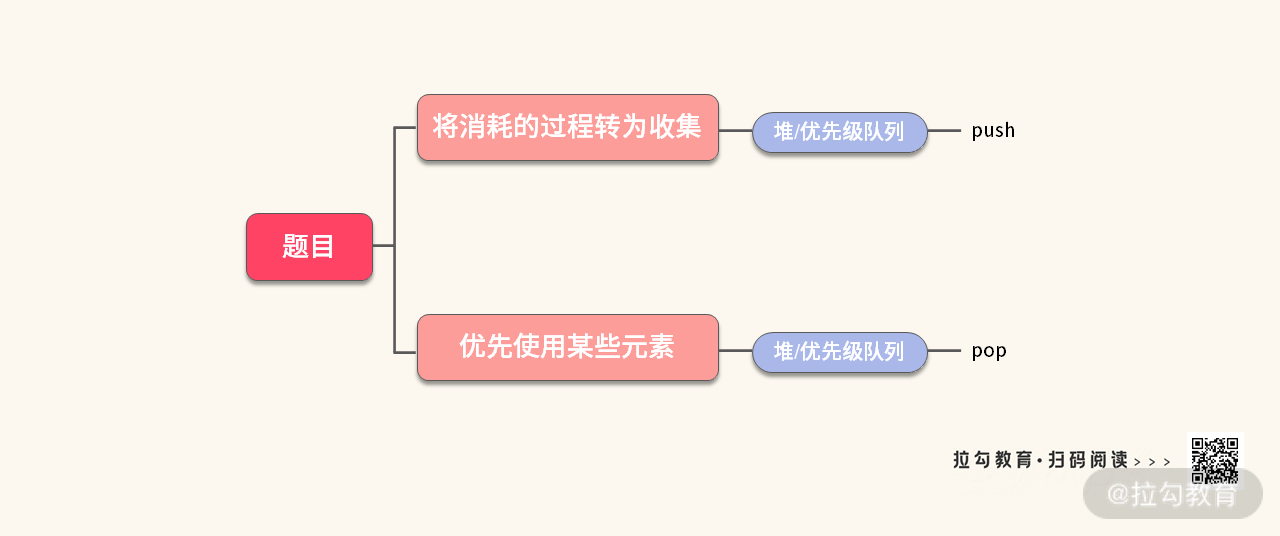
【小结】首先我们仔细总结一下这道题目的特点：

• 需要将消耗的过程，转换为存储的过程（记录在小本子上），对应堆的 push；
• 需要优先消除一些元素，对应堆的 pop。

与例 1 关于堆的题目相比，例 2 的求解过程不再那么直白，需要我们深入挖掘题目的特点，才能找到正确的解答方法——使用 push 和 pop。

此外，我们还能挖出一些不同的东西来——关于堆中元素需要弹出时的处理方式。在 Top K 问题里，当堆中元素个数超出 k 个时，就要执行 pop 操作。而这道题，将弹出元素的条件变成了堆中的总和不能超出砖块的数目。

练习题 6：一只蚂蚁在树下吃果子，第 i 天会掉 落 A[i] 个果子，这些果子会在接下来的 B[i] 天（即第 i+B[i] 天）立马坏掉不能吃。给定 A，B 两个数组，蚂蚁一天只能吃一个果子。吃不完了它可以存放起来。请问最多蚂蚁可以吃多少个果子。

输入：A = [3, 1], B = [3, 1]

输出：3

解释：我们假设下标从 1 开始：

第 1 天你吃 1 个第 1 天的果子

第 2 天吃 1 个第 1 天的果子，同时把第 2 天的果子存起来。

第 3 天吃 1 个第 1 天的果子，第 2 天的果子只能放 1 天，第 2 天的果子第 3 天坏了。

第 4 天没有果子吃了。

代码：Java/C++/Python

你可以自己尝试总结一下解决这类题目的思路和重点，然后再来参考我给出的思维导图：

例 3：汽车加油次数

【题目】一辆汽车携带 startFuel 升汽油从位置 0 出发前往位置 target，按顺序有一系列加油站 stations。第 i 个加油站位于 stations[i][0]，可以加 stations[i][1] 升油（一个加油站只能加一次）。如果想要到达 target，输出最少加油次数。如果不能到达 target，那么返回 -1。

两个条件：

1. 假设汽车油箱总是很大；
2. 假设行走一单位距离，消耗一升汽油。

示例：

输入：target = 100, startFuel = 10, stations = [[10, 60], [20, 30], [30, 30], [60, 40]]

输出：2

【分析】首先带着 10 升汽油，可以顺利开到 pos = 10 的加油站，加上 60 升汽油。然后直接开车到 pos = 60 的加油站，加上 40 升汽油就可以顺利到达 target = 100 处。所以最少需要加 2 次油。

在微软和头条都有同学遇到过这道题目。仔细读题之后，可以发现，需要加油的情况只有一种：汽车当前位置 + 车里剩余汽油 < 要到达的下一个目标地点。这里的下一个目标地点，有可能是 target，也有可能是加油站。

那么问题是，当我们发现汽油不够的时候，应该如何加油呢？题目最终目的是产生尽量少的加油次数，所以每次加油加得越多越好！这就找到了一个解题方向：应该挑油量最大的加油站进行加油。

假设有一个巨大无比的副油箱，每次经过加油站的时候，都可以把加油站里面的油放到副油箱里面存起来。缺油的时候，就从副油箱里把最大量的汽油加到车里（这里才算加一次油）。

1. 模拟

接下来我们就利用这个副油箱进行一下模拟，具体演示如下图所示（注意：副油箱里面的汽油不能算在已经加到车的汽油里，你可以认为它还放在后面座位上呢）：

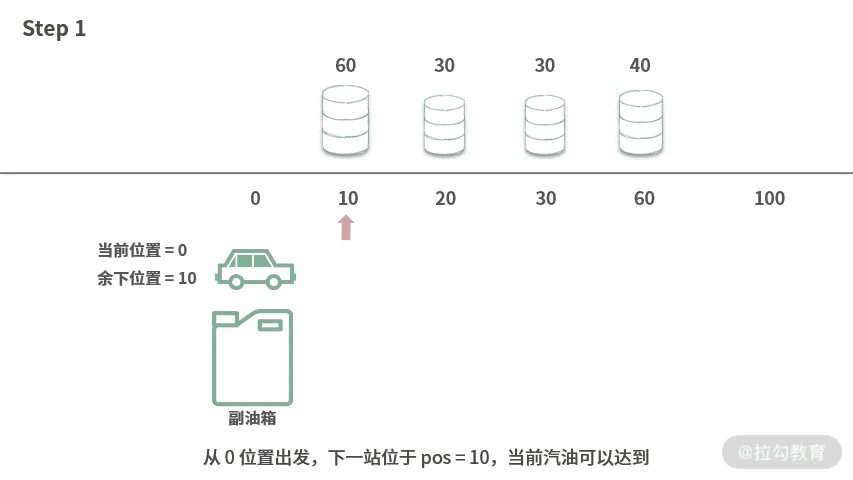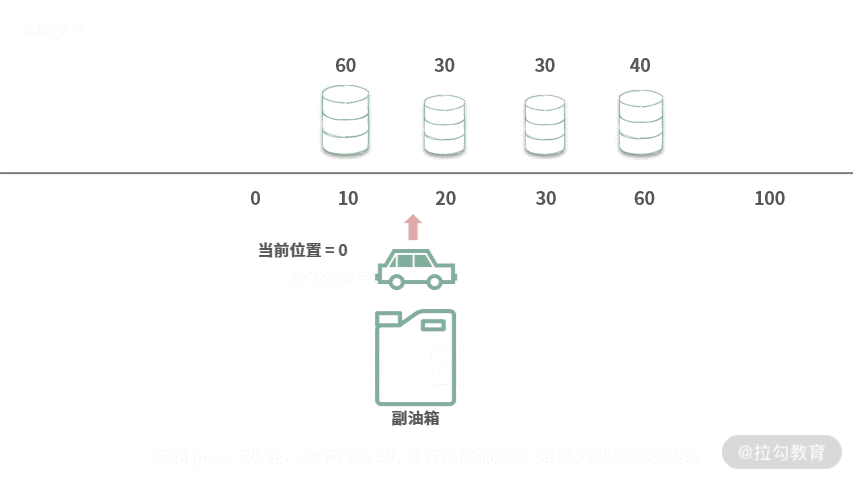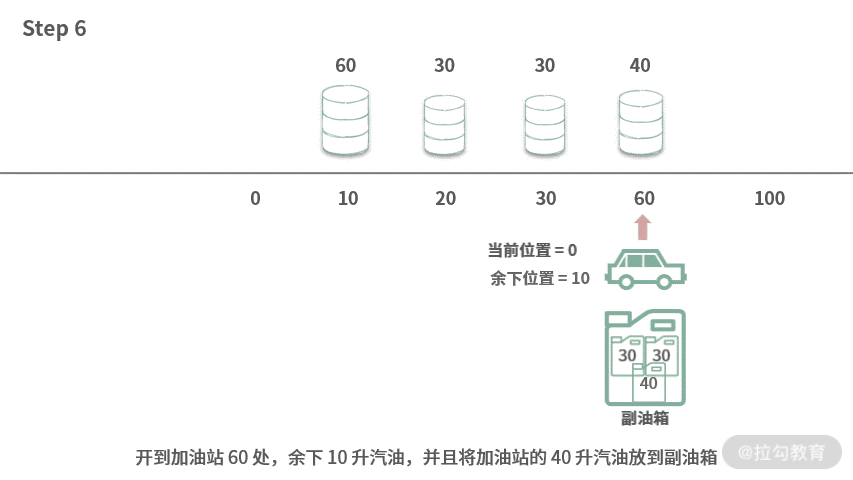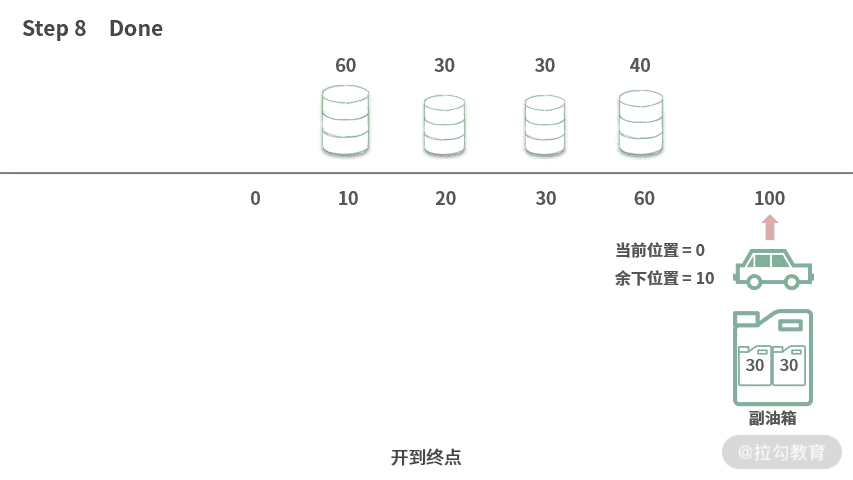
Step 1. 从 0 位置出发，下一站位于 pos = 10，当前汽油可以达到。
Step 2. 开到了 pos = 10，将 60 升汽油放到副油箱，此时余下汽油量为 0。
Step 3. 汽油里面的汽油不足开到 pos = 20 加油站，从副油箱中取出最多汽油 60 加上。第 1 次加油之后，余下油量变成 60。
Step 4. 开到 pos = 20 处，余下汽油 50, 并且将加油站的 30 升汽油放到副油箱。
Step 5. 开到 pos = 30 处，余下 40 升汽油，并且将加油站的 30 升汽油放到副油箱。
Step 6. 开到加油站 60 处，余下 10 升汽油，并且将加油站的 40 升汽油放到副油箱。
Step 7. 发现无法开到位置 100 处，那么将最多的汽油 40 升加到汽车里，此时余下汽油 50。
最后，成功开到了终点。

2. 规律

通过观察副油箱的操作，我们发现它的行为具有两个特点：

（1）每次经过加油站会把汽油加到副油箱

（2）缺油的时候，总是把最大升的汽油拿出来加上

这两个行为让我们联想到本讲学过的 push/pop 操作。并且每次 pop 的时候，都要弹出最大的元素，这又让我们想起了今天学过的堆（不过这里不再写堆的四种操作了），就用优先级队列吧。因为总是最大升的汽油优先。

3. 边界

在正式写代码前，你还是要考虑到以下 3 种情况：

（1）加油站的位置都小于 target

（2）某些加油站的位置等于 target

（3）有些加油站的位置大于 target

在处理的时候，可以将 target 也当成一个站。只不过这个站，并不提供汽油。这样处理起来更容易一些。

【代码】通过了前面的分析，此时我们应该撸起袖子开始写代码了，代码如下（解析在注释里）：

class Solution {
public int minRefuelStops(int target, int startFuel, int[][] stations) {
final int N = stations.length;
int i = 0;
int curPos = 0;
int fuelLeft = startFuel;
    Queue<Integer> Q = new PriorityQueue<>((v1, v2) -> v2 - v1);
int addFuelTimes = 0;
while (curPos + fuelLeft < target) {
int pos = target;
int fuel = 0;
if (i < N && stations[i][0] <= target) {
        pos = stations[i][0];
        fuel = stations[i][1];
      }
while (curPos + fuelLeft < pos) {
if (Q.isEmpty()) {
return -1;
        }
final int curMaxFuel = Q.peek();
        Q.poll();
        fuelLeft += curMaxFuel;
        addFuelTimes++;
      }
final int fuelCost = pos - curPos;
      fuelLeft -= fuelCost;
      curPos = pos;
if (fuel > 0) {
        Q.offer(fuel);
      }
      i++;
    }
return curPos + fuelLeft >= target ? addFuelTimes : -1;
  }
}

代码：Java/C++/Python

复杂度分析：最差情况下，需要把所有的油都收集起来，此时所有的油都需要有 push 操作，所以时间复杂度为 O(NlgN)，而空间复杂度为 O(N)。

【小结】首先，当你发现这道题属于 “消耗物品” 类题目，并且优先消耗较大的油箱时，脑海中应该联想前面我们讲过的关于堆的总结：

• 将消耗的过程转换为存储的过程，对应堆的 push 操作；
• 将优先选择大油桶的过程看成堆的 pop 操作。

经过一番分析，我们挖出了这道题背后的考点，以及优先级队列可能存在变化地方：

• 什么时候执行 push 操作？
• 什么时候执行 pop 操作？

练习题 7：在一个网络中有 N 台计算机，编号从 1~N，现在给定一些有向边，表示计算机之间网络传输使用的时间（ms），请问，从节点编号为 k 的计算机发出一个信号，需要多久才能让所有的计算机接收到信号。如果不能让所有人接收到信号，请输出 -1。

输入：N = 2, times = [1, 2, 100], k = 1

输出：100

解释：只有两个计算机 1，和计算机 2。从计算机 1 发送信息到计算机 2 需要 100ms。所以输出 100。

代码：Java/C++/Python

总结与延伸

至此，我们已经学习了堆的特性与实现。在了解了 push/pop 元素的复杂度为 logn 后，我们还需要知道考点可能出现在以下两个地方：

1. 什么时候 push 元素
2. 什么时候 pop 元素

这里我做了一个简单的归纳，并且列举了例题中的条件，你能在实战中补充一些其他有趣的条件吗？

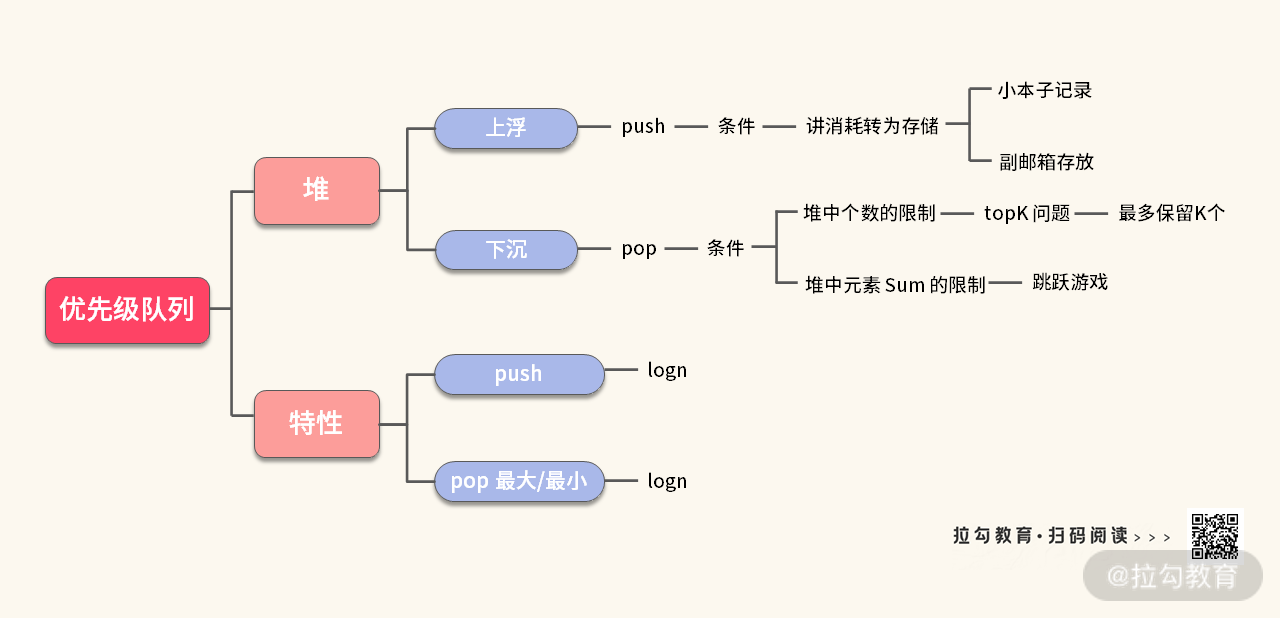
优先级队列非常有趣，也非常有用，在后面的广度优先搜索中，还会重拾这个知识， 帮助你解决更多的疑难问题。

思考题

最后我再给你留一道思考题：

来自 Google 的面试题。一个机器每隔一秒钟就会输出一个整数，请你写一个查询接口，输出所有已经得到的整数的中位数。中位数就是排序之后位于中间的数。如果数目为偶数，则是中间两个数的平均值。

代码：Java/C++/Python

你可以把答案写在评论区，我们一起讨论。接下来请和我一起踏上更加奇妙的算法与数据结构的旅程。让我们继续前进。后会有期，优先级队列！

下一讲将介绍 04 | 链表：如何利用 “假头，新链表，双指针” 解决链表题？（上）记得按时来探险。