18 | 单词接龙：如何巧用深搜与广搜的变形？

数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育

今天，我们继续尝试从不同的角度（方法）来求解一个题目，通过 “一题多解” 的训练，拓展我们的思维。“搜索类型” 的题目一直是面试考察的重点，其变形非常广，不过万变不离其宗，大部分解题方法仍然逃不开 BFS/DFS 这两个框架。

所以在本讲，我们将以一道经典的搜索题目为引，串联和使用前面学习过的各种知识点，比如：

• BFS / 双向 BFS
• DFS
• Dijkstra

具体介绍这类题目的分析和处理技巧，让你的面试得心应手。让我们马上开始。

题目

字典 wordList 中单词 beginWord 和 endWord 的转换序列是一个按下述规则形成的序列：

• 序列中第一个单词是 beginWord ；
• 序列中最后一个单词是 endWord，endWord 需要在 wordList 中；
• 每次转换只能改变一个字母；
• 转换过程中的中间单词必须是字典 wordList 中的单词。

给你两个单词 beginWord 和 endWord 和一个字典 wordList ，找到从 beginWord 到 endWord 的最短转换序列中的单词数目 。如果不存在这样的转换序列，返回 0。

输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]

输出：5

解释：一个最短转换序列是 “hit” → “hot” → “dot” → “dog” → “cog”，返回它的长度 5。

首先，这里需要重点说一下条件：

• beginWord != endWord；
• beginWord 可以不在 wordList 中；
• endWord 必须要在 wordList 中，如果不在 wordList 中，那么需要返回 0；
• 所有的单词长度都一样。

预处理

拿到题目，我们要做的第一件事，应该是去挖掘题目中的隐含条件。我们看到题目中有如下条件：

• 每次转换只能改变一个字母；
• 转换过程中的中间单词必须是 wordList 里面的单词。

如果将每一次的转换，看成是图中两个点的连接，题目的最终问题就是希望我们找到图中给定两个点的最短距离。

如果把单词看成图的点，那么对应图的边又是什么呢？

注意：这里提到的图，都是指算法中的图 Graph，而不是图画 Picture。

边的由来

当我们有 word = “hit”，如果改变其中一个字母，就可以生成 “hat”。但是，我们立马发现 wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”] 并不存在单词 “hat”。

如果从图的角度来看，可以认为 <”hit”, “hat”> 这条边不存在。那么接下来，我们再看一下成功的情况。

当我们有 word = “hit”，如果改变一个字母，生成 “hot”，由于 wordList[0] == “hot”，因此，这种转换 “hit” ←→ “hot” 是合法的，那么，可以认为边 <”hit”, “hot”> 是存在的。

边的无向性

对于单词转换来说，当 word=”hit” 可以转换成 “hot” 的时候，那么反过来 “hot” 也可以转换为 “hit”。因此，当我们得到一条边的时候，这条边就是一条无向边。

接下来我们再分析一下这类题的考点。

考点

在 “13 | 搜索：如何掌握 DFS 与 BFS 的解题套路？” 中，我们学习的大部分关于 “图” 的题目，都是明确地知道图的边，或者题目中给出了图的边。

但是，在这个题中，并没有明确地给出图的边。所有的边都需要依赖一定的条件动态生成。我们可以利用伪代码，表示边的生成，代码如下（解析在注释里）：

for word in Graph:
    startPoint = word 
for c in word:
        oldChar = c
for toChar in 'a'~'z':
             c = toChar
             endPoint = word
if endPoint in wordList:
        c = oldChar

有了图的重建，再给定输入，代码如下：

beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log","cog"]

经过上述操作，就可以得到题目中图的表示：

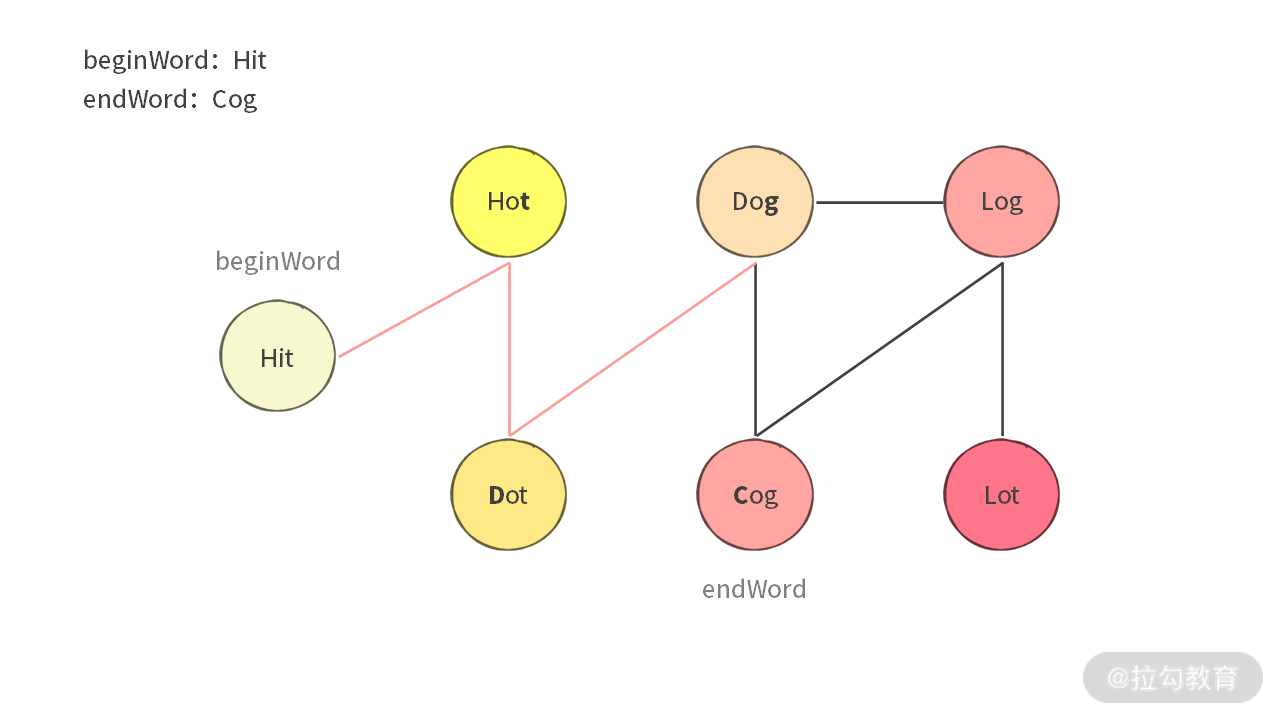
转换

如何利用字符串表示图中的点，就需要两个字符串来表示一条边。为了压缩这部分信息，我们采用整数来表示字符串。优点有以下几个方面。

• 字符串的处理不方便，必须使用哈希表。如果是整数表示图中的点，那么我们可以使用数组记录点的信息。
• 字符串的运算速度没有整数快。
• 我们在学习图算法的时候，大部分时候都是使用整数来表示图中的点，相对来说，对代码更加熟悉。

基于以上三个原因，我们决定将 String 表示一个点，转换为用整数表示一个点。转换的思想也比较简单：利用哈希表将不同的字符串映射到不同的整数上即可。

这里我们直接给出 “建图”+“转换” 的代码，如下所示（解析在注释里）：

class Solution {
private Map<String, Integer> wordID = null;
private List<Integer> Graph[] = null;
boolean buildGraph(String beginWord,
                       String endWord,
                       List<String> wordList) {
if (beginWord.compareTo(endWord) == 0) {
return false;
        }
        wordID = new HashMap<>();
int id = 0;
for (String word: wordList) {
if (!wordID.containsKey(word)) {
                wordID.put(word, id++);
            }
        }
if (!wordID.containsKey(endWord)) {
return false;
        }
if (!wordID.containsKey(beginWord)) {
            wordID.put(beginWord, id++);
            wordList.add(beginWord);
        }
        Graph = new ArrayList[wordID.size()];
for (int i = 0; i < wordID.size(); i++) {
            Graph[i] = new ArrayList<>();
        }
for (String word: wordList) {
final int from = wordID.get(word);
byte[] wordBytes = word.getBytes();
for (int i = 0; i < wordBytes.length; i++) {
byte old = wordBytes[i];
for (byte toByte = 'a'; toByte <= 'z'; toByte++) {
                    wordBytes[i] = toByte;
                    String toWord = new String(wordBytes);
if (wordID.containsKey(toWord)) {
int to = wordID.get(toWord);
                        Graph[from].add(to);
                    }
                }
                wordBytes[i] = old;
            }
        }
return true;
    }
public int ladderLength(String beginWord,
                            String endWord,
                            List<String> wordList) {
if (!buildGraph(beginWord, endWord, wordList)) {
return 0;
        }
    }
}

注意：在后文的代码中，我不再罗列 buildGraph 函数的详细代码，所有引用到 buildGraph 代码的地方，都是指这里的 buildGraph() 函数。

当我们建好图之后，问题就变成：

• 给定一个无向图；
• 如何求图中两个点的最短距离。

不过，根据题意，还需要注意题目要求输出的是 “最短转换序列”：

一个最短转换序列是 “hit” → “hot” → “dot” → “dog” → “cog”，返回它的长度 5。

因此，最短序列等价于最短路径上的点的个数。而我们平时求的最短路径实际上是最短路径上边的数目。因此：

最短转换序列长度 = 最短路径长度 + 1

那么，到这里，我们已经将陌生的题目成功转变成非常熟悉的问题：求图中两个点的最短距离。

接下来，我们看一下具体如何破解 “最短路径” 问题，其实我们在“13 | 搜索：如何掌握 DFS 与 BFS 的解题套路？”的 “例 2 和例 4” 都学习过，你可以返回去再复习一下，以便加深对这个经典问题的理解。

BFS 算法

求两个点的最短路径的时候，我们可以直接用 BFS。为什么呢？

你应该还记得，我们在 “13 | 搜索：如何掌握 DFS 与 BFS 的解题套路？” 中提到过 BFS 的特点：

在搜索的时候，若想知道一些关于 “最近 / 最快 / 最少” 之类问题的答案，往往采用 BFS 更加适合。

因此，在这里，我们直接使用 BFS 算法。如果从 beginWord 开始搜索，那么 BFS 的搜索过程可以表达成一个 “雷达波搜索” 的样子——每一轮搜索都会往外扩散一圈。

你可以结合下图展示的 BFS 的搜索过程示意图进一步思考，我们从 beginWord = “hit” 开始搜索，直接到找到 endWord = “cog” 时停止。

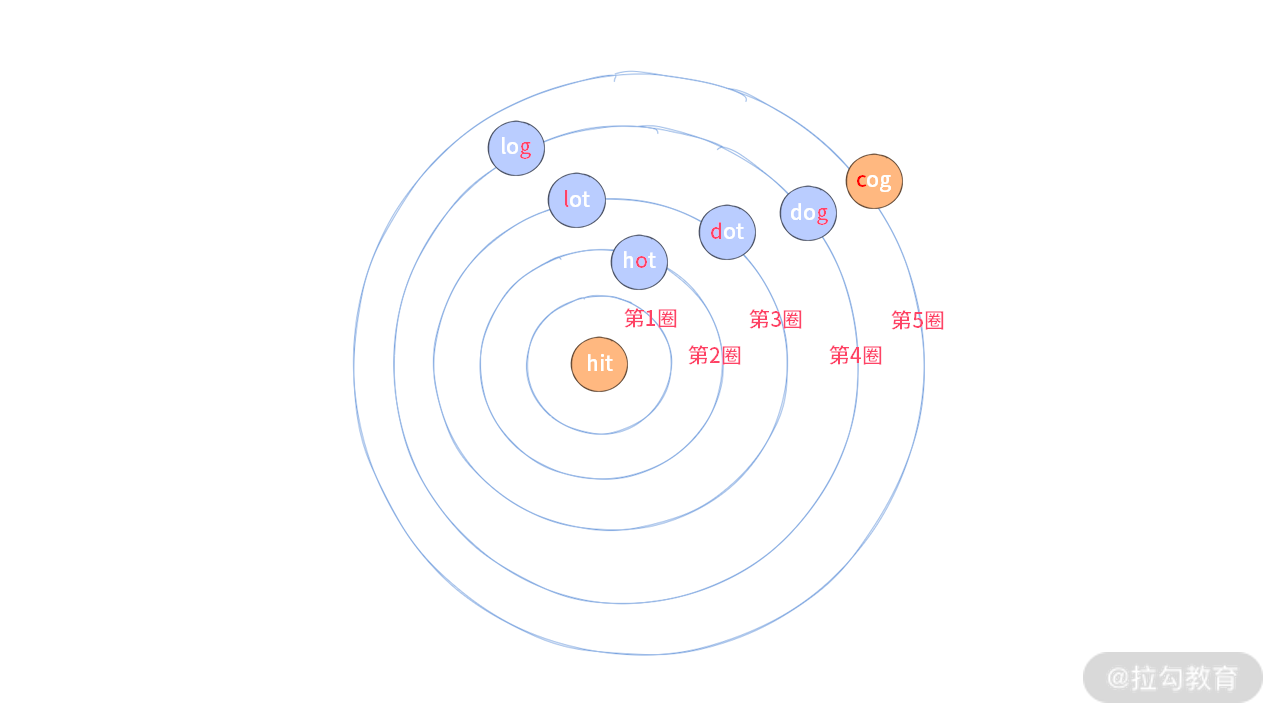
注：这里第 1 圈就是 hit 自身，蓝色圈表示 1 次搜索。

那么在写代码的时候，我们可以使用类似的技巧进行 BFS。在每一层，我们都使用一个 ArrayList 来表示。那么，可以写出基于 BFS 的代码如下（解析在注释里）：

class Solution {
public int ladderLength(String beginWord,
                          String endWord,
                          List<String> wordList) {
if (!buildGraph(beginWord, endWord, wordList)) {
return 0;
    }
final int src = wordID.get(beginWord);
final int dst = wordID.get(endWord);
    List<Integer> cur = new ArrayList<>();
    cur.add(src);
    List<Integer> next = new ArrayList<>();
boolean[] vis = new boolean[wordID.size()];
    vis[src] = true;
int step = 0;
while (!cur.isEmpty()) {
      next.clear();
      step++;
for (Integer curNode : cur) {
if (curNode == dst) {
return step;
        }
for (Integer nextNode : Graph[curNode]) {
if (!vis[nextNode]) {
            next.add(nextNode);
            vis[nextNode] = true;
          }
        }
      }
      List<Integer> tmp = cur;
      cur = next;
      next = tmp;
    }
return 0;
  }
}

代码：Java/C++/Python

复杂度分析：（假设我们有 N 个单词，每个单词的长度为 M。每个单词需要更改每个位置的字母来生成新的单词）这里时间复杂度需要分为两步。

第一步：预处理建图

1. 时间复杂度

1）一共需要处理 N * M 个字母，每个字母要替换 26 次。替换之后生成的长度为 M 的新单词需要去哈希表中检验，每次去哈希表中检查一个单词需要的时间复杂度为 O(M)。

2）建图时间复杂度为 O(N M M 26)，我们可以把常数 26 去掉，因此时间复杂度为 O(N M * M)。

2. 空间复杂度

1）建图时需要建立一个有 N 个 Item，并且每个 Item 长度为 M 的哈希表。因此，哈希表空间复杂度为 O(N * M)。

2）Graph 需要占用 O(N * N) 的空间。

第二步：BFS

1. 时间复杂度

在后面 BFS 搜索的过程中，由于不会访问已访问过的点，相当于所有的点被遍历一遍，所以时间复杂度为 O(N)。

2. 空间复杂度

最差情况下，需要把所有的点都放到 Array 中，此时空间复杂度为 O(N)。

综上，整个问题的时间复杂度为 O(N M M)，空间复杂度为 O(max(N2, N * M))。

双向 BFS

如果说前面的 BFS 是 “一个人” 苦苦地用雷达搜索（后文中称为单向 BFS），那么会不会存在从两个方向进行搜索的情况呢？我们尝试分析一下。如果要找的目标也用雷达开启搜索，那么当两者有交互的时候，就可以认为找到了最短路径。

这种方法我们称为双向 BFS。两者的搜索过程如下图所示：

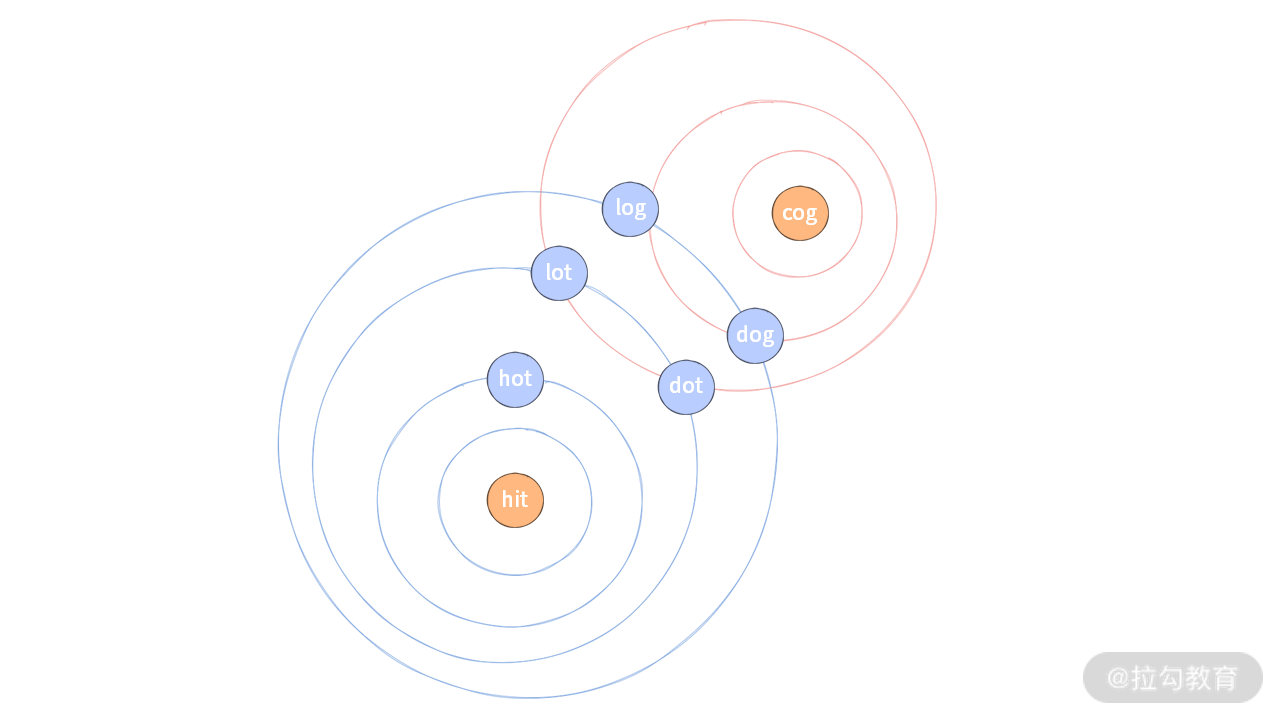
实际上，我们在写双向 BFS 的时候，两边不会同时开启搜索。而是采用一种策略：优先搜索范围更小的。

主要原因在于：

• 我们写算法的时候，往往不需要多线程；
• 优先搜索范围更小的，可以节省更多的内存，因为要存放的信息变少了。

基于这种双向 BFS 的想法，可以写出代码如下（解析在注释里）：

class Solution {
public int ladderLength(String beginWord,
                          String endWord,
                          List<String> wordList){
if (!buildGraph(beginWord, endWord, wordList)) {
return 0;
    }
final int srcNode = wordID.get(beginWord);
final int dstNode = wordID.get(endWord);
    Set<Integer> src = new HashSet<>();
    src.add(srcNode);
    Set<Integer> dst = new HashSet<>();
    dst.add(dstNode);
final int srcVisTag = 1;
final int dstVisTag = 2;
int[] vis = new int[wordID.size()];
    vis[srcNode] = srcVisTag;
    vis[dstNode] = dstVisTag;
int step = 0;
while (!src.isEmpty() && !dst.isEmpty()) {
      step++;
for (Integer node : dst) {
if (src.contains(node)) {
return step;
        }
      }
final int visTag = src.size() < dst.size() ?
            srcVisTag : dstVisTag;
      Set<Integer> tmp = src.size() < dst.size() ? src : dst;
      Set<Integer> next = new HashSet<>();
for (int startNode : tmp) {
for (int nextNode : Graph[startNode]) {
if (vis[nextNode] != visTag) {
            vis[nextNode] = visTag;
            next.add(nextNode);
          }
        }
      }
if (src.size() < dst.size()) {
        src = next;
      } else {
        dst = next;
      }
    }
return 0;
  }
}

代码：Java/C++/Python

这里，我们将双向 BFS 与单向 BFS 进行一个比较，如下表所示：

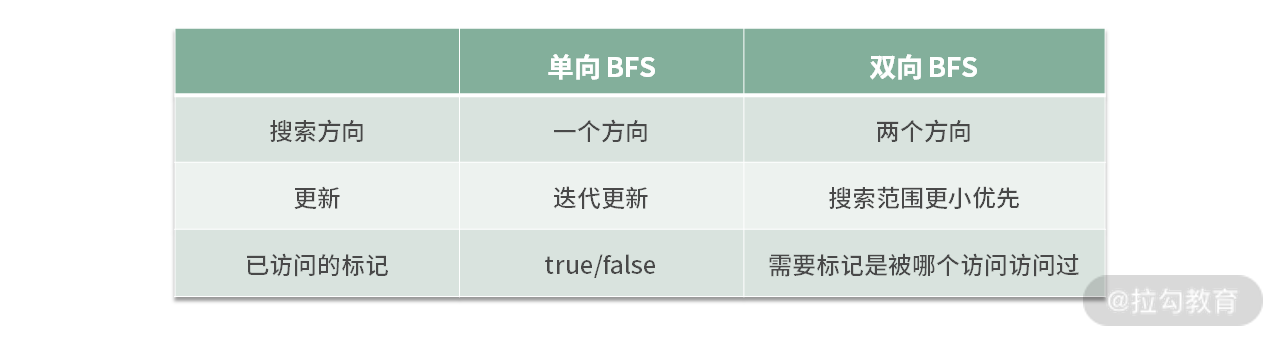
那么，双向 BFS 主要的优化在于：

• 搜索时需要存放的信息更小了（因为搜索范围更小的优先），因此更加节省内存；
• 由于要处理的信息变少了，那么查找起来也会更快一些。

不过双向 BFS 还是在单向 BFS 上做常数上的优化。最差情况下，时间复杂度与空间复杂度仍然是在一个数量级的。

Dijkstra 算法

一般而言，最短路径问题，有三种：

• 两点之间的最短路径（BFS 算法 / Dijkstra 算法 / BF 算法，即 Bellman-Ford 算法）；
• 一个点到其他所有点的最短路径（Dijkstra 算法 / BF 算法）；
• 每两点之间的最短路径（Floyd 算法）。

现在，我们先讨论一下，在计算两点间的最短路径的时候，什么时候应该使用 BFS 算法，什么时候应该使用 Dijkstra 算法？

• 当图中边的权重都是 1 的时候，最好的办法是使用 BFS 算法。
• 当图中边的权重非负的时候，最好的办法是使用 Dijkstra 算法。
• 当图中的边的权重存在负值的时候，最好的办法是采用 BF 算法。

实际上，我们可以将权重为 1 的时候，看成权重不同的特例。那么，这里我们应该也可以使用 Dijkstra 算法。根据 Dijkstra 算法的思路（“03 | 优先级队列：堆与优先级队列，筛选最优元素”的 “练习题 7” 用到了 Dijkstra，以及“13 | 搜索：如何掌握 DFS 与 BFS 的解题套路？” 的 “例 5”），我们可以写出代码如下（解析在注释里）：

class Solution {
public int ladderLength(String beginWord,
                          String endWord,
                          List<String> wordList) {
if (!buildGraph(beginWord, endWord, wordList)) {
return 0;
    }
final int src = wordID.get(beginWord);
final int target = wordID.get(endWord);
int[] dist = new int[wordID.size()];
for (int i = 0; i < dist.length; i++) {
      dist[i] = wordID.size() * wordID.size() + 100;
    }
    dist[src] = 0;
    Queue<Integer> Q = new PriorityQueue<>(
            (v1, v2) -> dist[v1] - dist[v2]);
    Q.add(src);
while (!Q.isEmpty()) {
final int startNode = Q.poll();
final int startDist = dist[startNode];
for (int nextNode : Graph[startNode]) {
final int nextDist = startDist + 1;
if (dist[nextNode] > nextDist) {
          dist[nextNode] = nextDist;
          Q.add(nextNode);
        }
      }
    }
return dist[target] > wordID.size() ?
0 : dist[target] + 1;
  }
}

代码：Java/C++/Python

复杂度分析：时间复杂度，由于 Dijkstra 算法的时间复杂度在有 N 个点的情况下，复杂度为 O(NlgN)。但是，整个题目的时间复杂度与空间复杂度仍然由 buildGraph 函数主导。与 BFS 的时间复杂度相同。

我们再对 Dijkstra 算法做个小小的总结，在使用 Dijkstra 算法的时候，有以下特点：

• 并没有使用 vis 数组来进行标记；
• 而是当发现一个点的最小距离变得更小的时候，就需要放到优先级队列中，然后重新展开搜索。

本讲中，我们提到了 BF 算法。不过 BF 算法在有 N 个点，E 条边的情况下，时间复杂度会达到 O(N x E)。在本题中，当单词长度为 M 时，最差情况下，一个单词可以有 M x 26 条边。一个图中的边可以达到 N x M x 26。此时，时间复杂度达到 O(N x N x M x 26)，会出现超时的情况。关于这种情况，你可以自己求解一下下面这道练习题，本讲不再详细讨论。

练习题 1：有 N 个网络结点，标记为 1 到 N。给定一个列表 times，表示信号经过有向边的传递时间。 times[i] = (u, v, w)，其中 u 是源结点，v 是目标结点，w 是一个信号从源结点传递到目标结点的时间。

现在，我们从某个结点 K 发出一个信号。需要多久才能使所有结点都收到信号？如果不能使所有结点收到信号，则返回 -1。

代码：Java/C++/Python

DFS 算法

不知道你有没有从 Dijkstra 的算法中找到灵感？在遍历的时候，我们不再使用 vis 数组来记录一个点是否被访问，而是利用最小距离是否被更新作为条件。

那么在 DFS 的时候，是不是也可以这样操作？比如：

private void dfs(List<Integer> G[], int start, int[] dist)
  {
for (int nextNode : G[start]) { 
final int nextDist = dist[start] + 1;
if (nextDist < dist[nextNode]) { 
        dist[nextNode] = nextDist;
        dfs(G, nextNode, dist);        
      }
    }
  }

那么，基于这种距离更新，就重新展开 DFS 的搜索方法，我们也可以写出新的 DFS 算法来解决这道题，代码如下（解析在注释里）：

class Solution {
private void dfs(List<Integer> G[], int start, int[] dist)
  {
for (int nextNode : G[start]) {
final int nextDist = dist[start] + 1;
if (nextDist < dist[nextNode]) {
        dist[nextNode] = nextDist;
        dfs(G, nextNode, dist);
      }
    }
  }
public int ladderLength(String beginWord,
                          String endWord,
                          List<String> wordList) {
if (!buildGraph(beginWord, endWord, wordList)) {
return 0;
    }
final int src = wordID.get(beginWord);
final int dst = wordID.get(endWord);
int[] dist = new int[wordID.size()];
int maxPathLength = wordID.size() + 1024;
for (int i = 0; i < dist.length; i++) {
      dist[i] = maxPathLength;
    }
    dist[src] = 0;
    dfs(Graph, src, dist);
return dist[dst] >= maxPathLength ? 0 : dist[dst] + 1;
  }
}

代码：Java/C++/Python

复杂度分析：假设一共有 N 个点，那么最差情况下，每个点会被其他点最多更新 N 次。因此，最差时间复杂度为 O(N2)。但是就整个题目而言，时间复杂度由构建图 buildGraph 的部分主导。综上，时间复杂度为 O(N M M)，空间复杂度为 O(max(N2N * M))。

那么，接下来，我们考虑一下，Dijkstra 算法与 DFS 算法不同的地方。

虽然 Dijkstra 与 DFS 都不会再用到 vis 数组，并且都在点 nextNode 的距离被更新，然后重新展开搜索。但是依然存在不同的地方。

• Dijkstra 算法是从优先级队列中拿出最优的点重新展开搜索。而且 Dijkstra 算法在用一个点更新的时候，会把这个点相邻的所有点更新之后，再重新展开搜索。
• 而 DFS 算法却是立马从点 nextNode 重新展开搜索。

那么，有没有可能将 DFS 也改成 Dijkstra 这样呢？我们是不是发明了 DFS 也可以实现 Dijkstra 算法呢？基于这种思路，对 DFS 算法进行一下改写，代码如下（解析在注释里）：

class Solution {
private int[] dist = null;
private Queue<Integer> Q = 
new PriorityQueue<>((v1, v2) -> dist[v1] - dist[v2]);
private void dfs() {
if (Q.isEmpty()) {
return;
    }
final int startNode = Q.poll();
for (int nextNode : Graph[startNode]) {
final int nextDist = dist[startNode] + 1;
if (nextDist < dist[nextNode]) {
        dist[nextNode] = nextDist;
        Q.add(nextNode);
      }
    }
    dfs();
  }
public int ladderLength(String beginWord,
                          String endWord,
                          List<String> wordList) {
if (!buildGraph(beginWord, endWord, wordList)) {
return 0;
    }
final int src = wordID.get(beginWord);
final int dst = wordID.get(endWord);
    dist = new int[wordID.size()];
int maxPathLength = wordID.size() + 1024;
for (int i = 0; i < dist.length; i++) {
      dist[i] = maxPathLength;
    }
    dist[src] = 0;
    Q.add(src);
    dfs();
return dist[dst] >= maxPathLength ? 0 : dist[dst] + 1;
  }
}

代码：Java/C++/Python

我们发现，经过上述处理的 DFS，本质上与 Dijkstra 算法是一样的。在这里，我们将不同的算法的特点加以迁移（从原本是 Dijkstra 的特点，迁移到 DFS 算法），让不同的算法可以取得同样的效果。

总结

这一讲中，我们再次通过一个题目，挖掘了题目的信息 + 考点。

• 信息：需要通过一定的条件生成边。
• 考点：两点的最短路径。

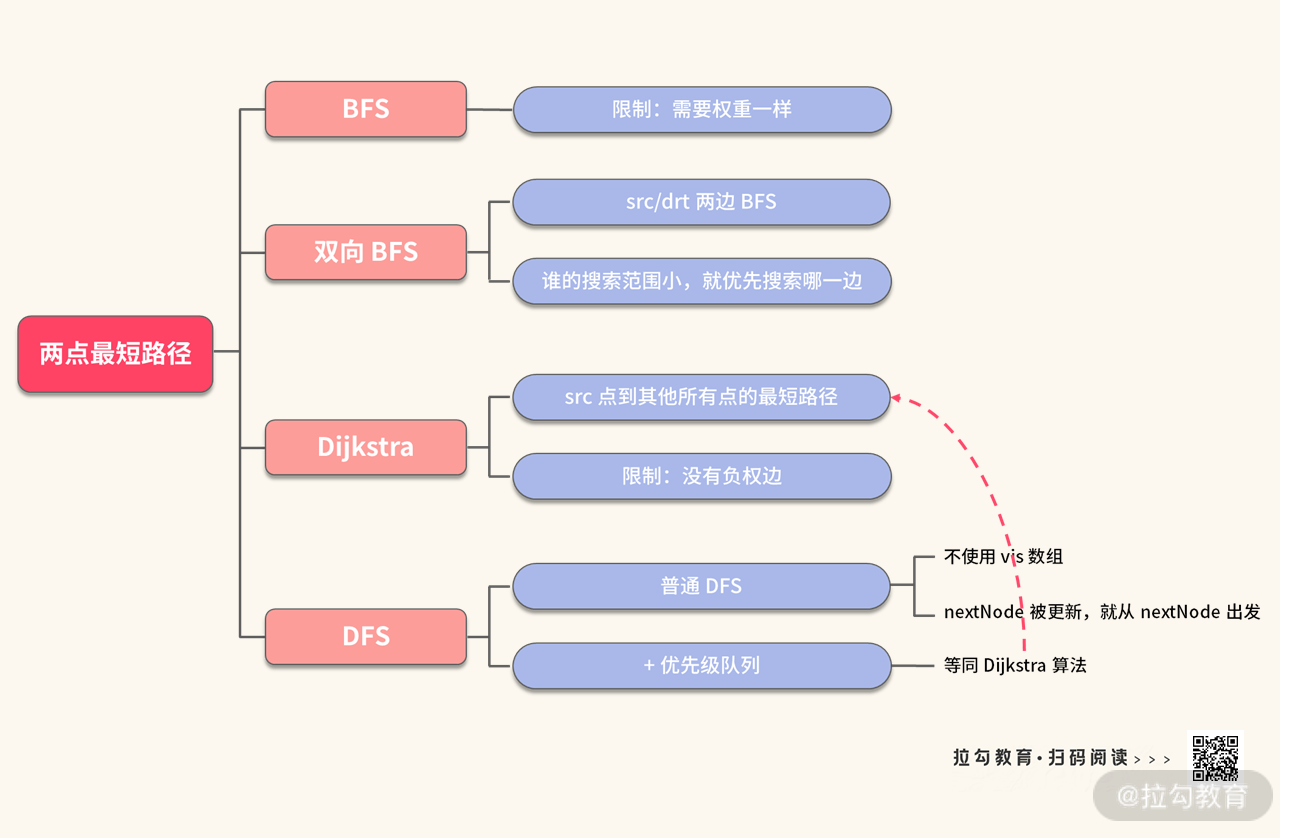
当拿到这两部分信息之后，我们首先进行题目的预处理：建图。通过建图，让题目回到了一个我们非常熟悉的知识点：两点最短路径。接来下就是匹配到了已经学过的各种知识点，轮番上阵，也就展开了不同的破题方法。最后，我把这个题目中用到的知识点整理在下面这张思维导图中，你可以参考下图梳理一遍今天学到的重点知识。

思考题

我再给你留一道思考题：在本讲介绍的题目基础上，我们找到最短的转换序列的长度之后。如果要输出所有的最短转换序列，应该怎么办呢？

输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]

输出：[[“hit”,”hot”,”dot”,”dog”,”cog”],[“hit”,”hot”,”lot”,”log”,”cog”]]

解释：存在 2 种最短的转换序列：

“hit” -> “hot” -> “dot” -> “dog” -> “cog”

“hit” -> “hot” -> “lot” -> “log” -> “cog”

代码：Java/C++/Python

你可以自己尝试求解这道题目，把答案写在留言区，我们一起讨论。关于单词转换的题目就介绍到这里。接下来，下一讲介绍 “19 | 最小体力消耗路径：如何突破经典题型，掌握解题模板”，让我们继续前进。

附录：题目出处和代码汇总

| 题目 | 测试链接 | BFS 代码：Java/C++/Python
双向 BFS 代码：Java/C++/Python
Dijkstra 代码：Java/C++/Python
DFS + Q 代码：Java/C++/Python |
| —- | —- | —- |
| 练习题 1 | 测试链接 | 代码：Java/C++/Python |
| 思考题 | 测试链接 | 代码：Java/C++/Python |