数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
贪心算法(Greedy Algorithms)指的是求解问题时,总是做出在当前看来是最好的选择。 一个全局最优解可以通过选择局部最优解来达到。
贪心算法的运用非常广泛,比如哈夫曼(Huffman)树,单源最短路径(Dijkstra),构建最小生成树的 Prim 算法和 Kruskal 算法等。
学完这一讲,你将会收获:
- 贪心算法类题目的特点
- 贪心算法的解题思路
注:贪心算法没有模板可以套,其重点在于对题目的分析,对结论的推导。因此,这一讲,我们不再延用 “模拟、规律、匹配、画图” 四步分析法,而是将重点放在介绍一些题目是如何演变而来的,以及如何推导出贪心所用的结论。我会尝试用尽量少的数学公式,且让你能看懂的方式来讲解。
贪心的特点
面试中考察贪心算法的题目必然具备以下2 个特点,这里我用最通俗的话给你描述。
特点 1:只选局部最优解
在求解过程中,我们可以通过每一步都选择最优解,最终得到整个问题的最优解。下面我们通过一个简单的题目:寻找数组中最大的数,进一步说明一下这个特点。
int maxValue(int[] A) {final int N = A == null ? 0 : A.length;int maxValue = Integer.MIN_VALUE;for (int i = 0; i < N; i++) {maxValue = Math.max(maxValue, A[i]);}return maxValue;}
首先: 在一个初始集(这里是一个空集),设置一个初始解。在这里,我们设置为 Integer.MIN_VALUE。
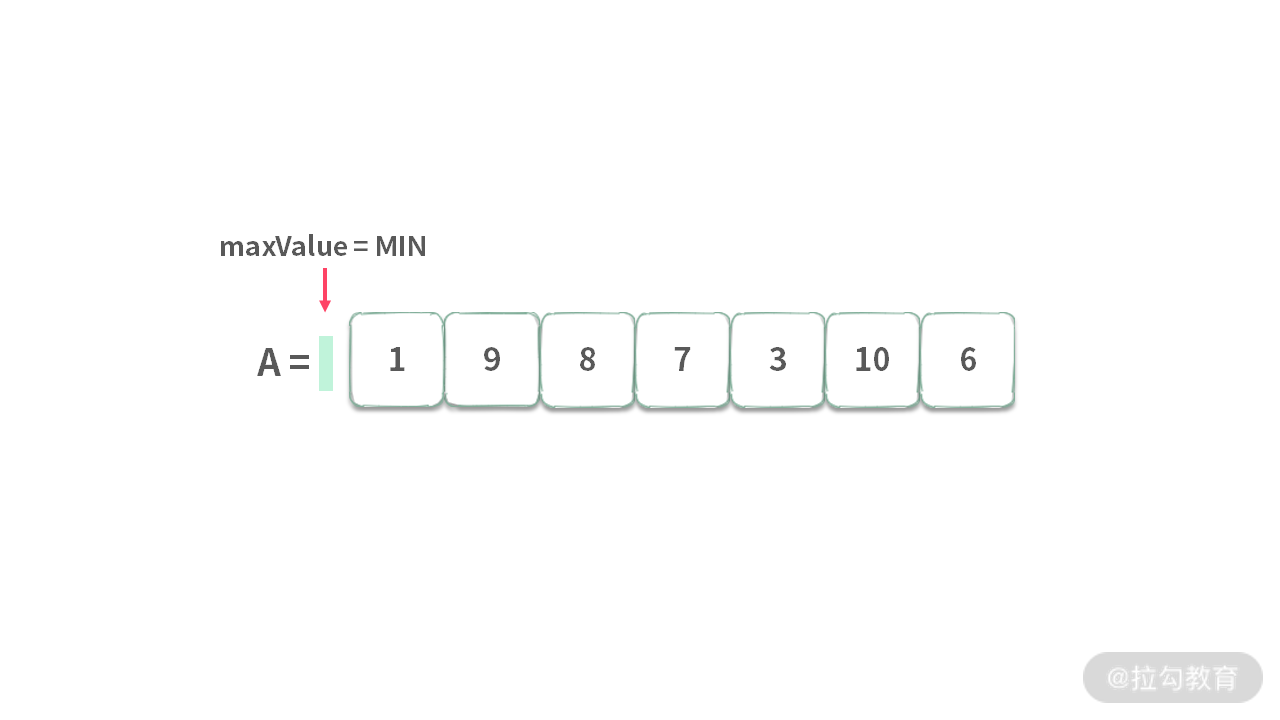
迭代:当有新元素进来的时候,我们需要迭代当前最优解。迭代后的最优解是已知数据的最优解。
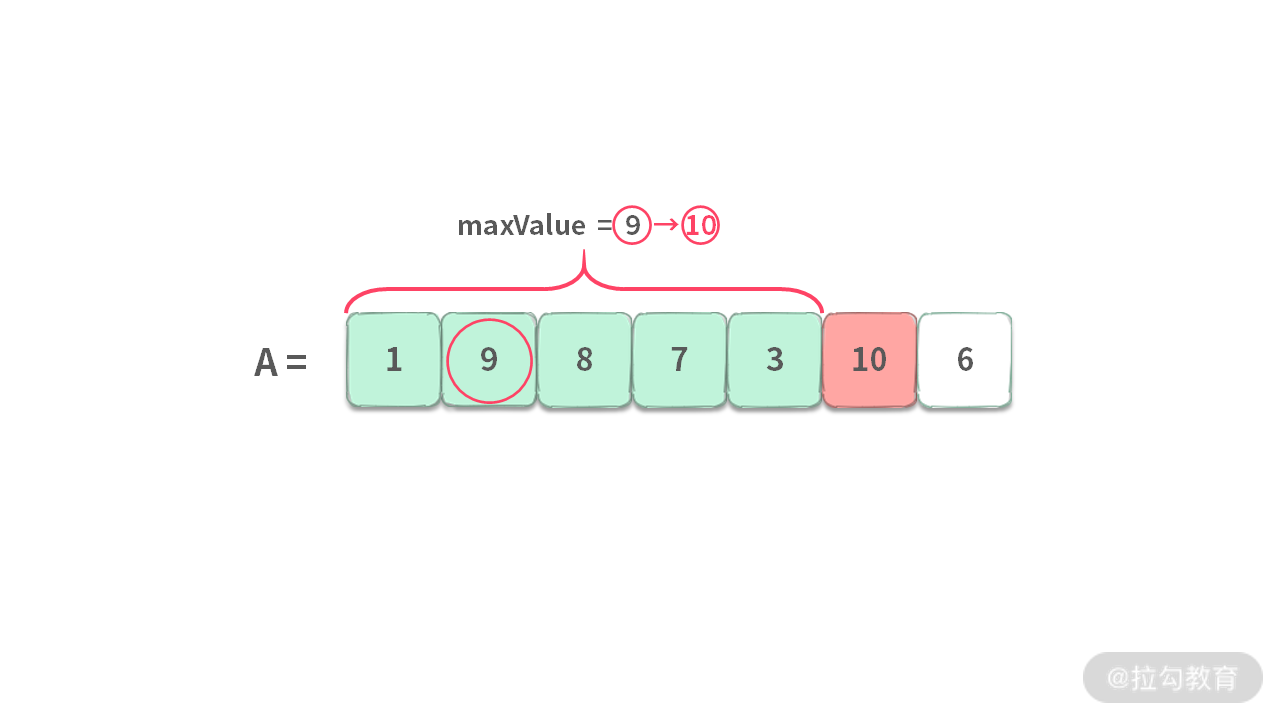
答案:当处理完所有的数据之后,当前最优解立马变身全局最优解。
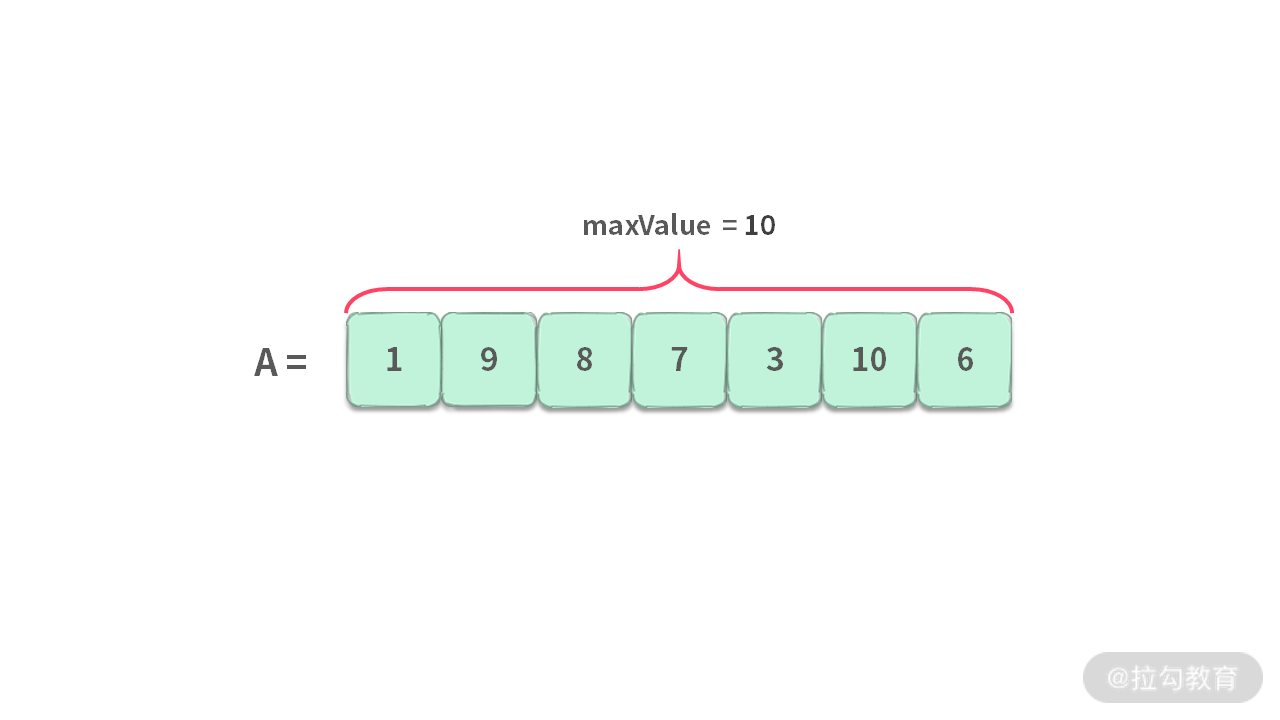
由此,我们也可以看出,贪心算法在操作的时候,总是把局部次优解直接扔掉,保留局部最优解,最终得到整个问题的最优解。
特点 2:不能 “逆袭”
下面我们用一道题目说明什么是 “逆袭”。给定如下图所示的图形,从上往下走的时候,只能走到相邻格子的左边或者右边。求从顶部走到底部的最大和。
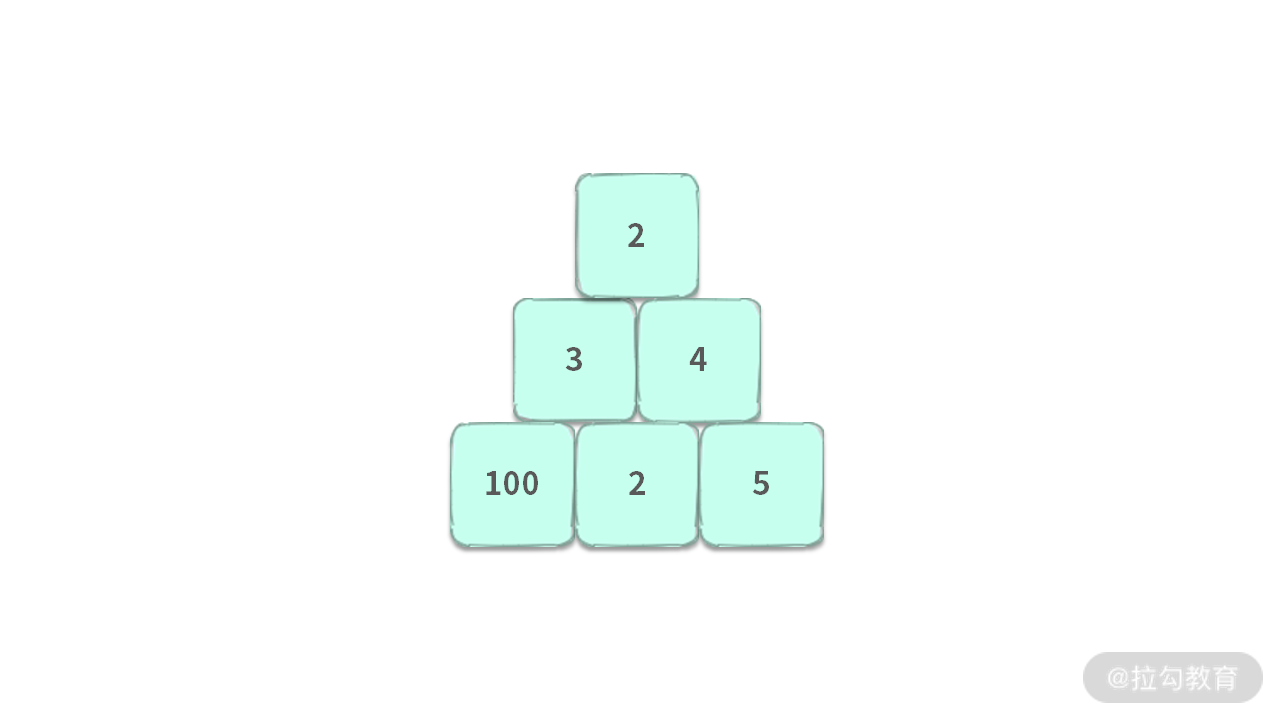
比如,这里我们给出合法与不合法的两种情况,如下图所示:
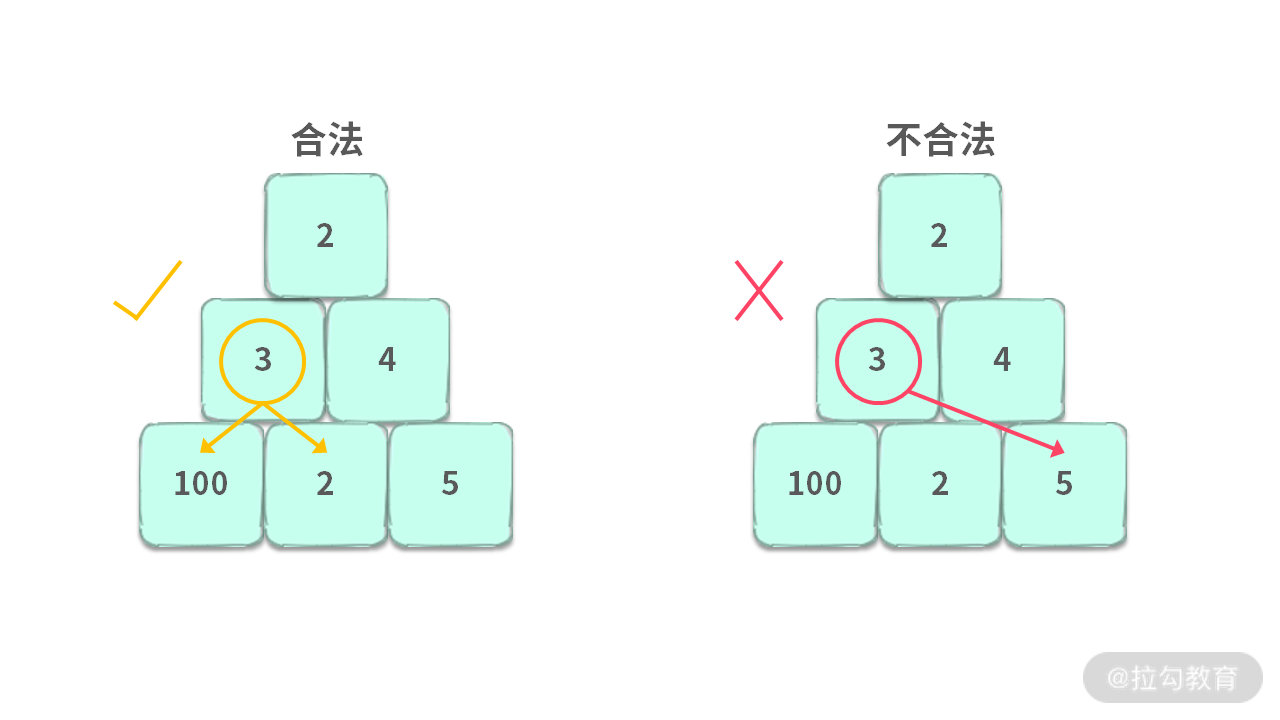
如果使用贪心算法求解这个问题,你可以结合下图进行思考:
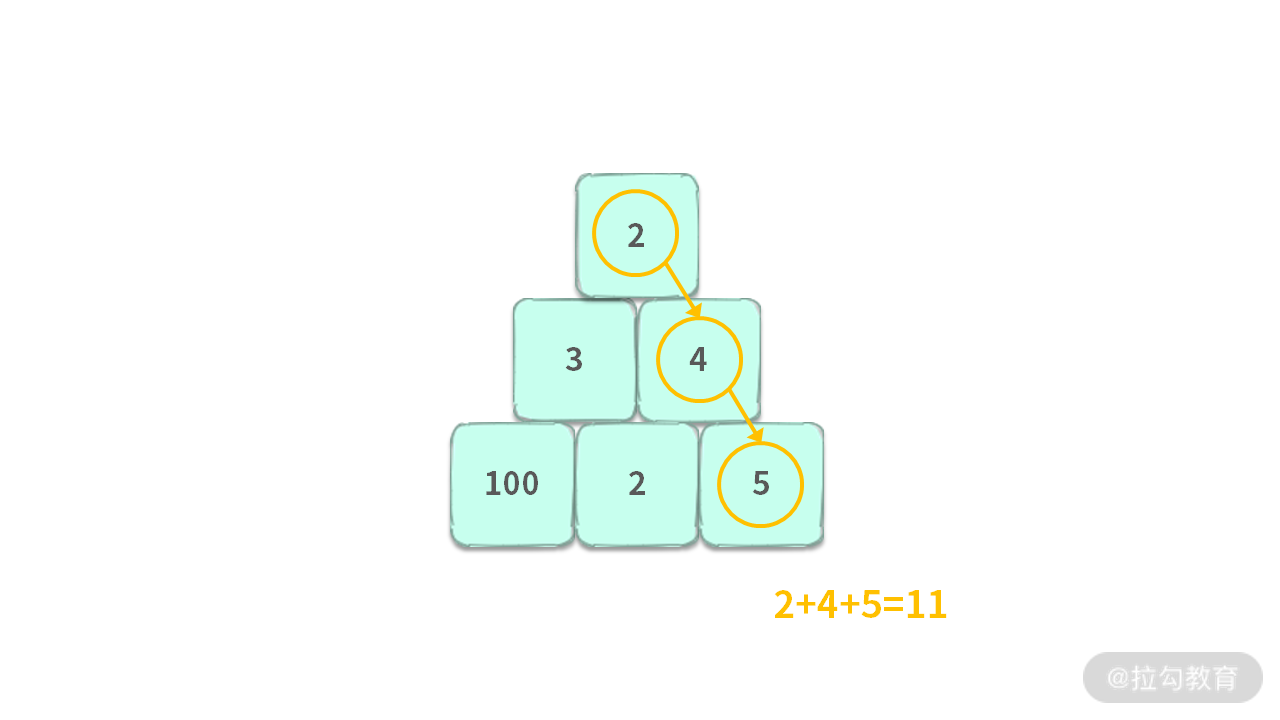
如果在每一步,我们总是选择当前能选择的最大值,那么得到的解就不是最优解。因为最优解是 2 + 3 + 100 = 105。
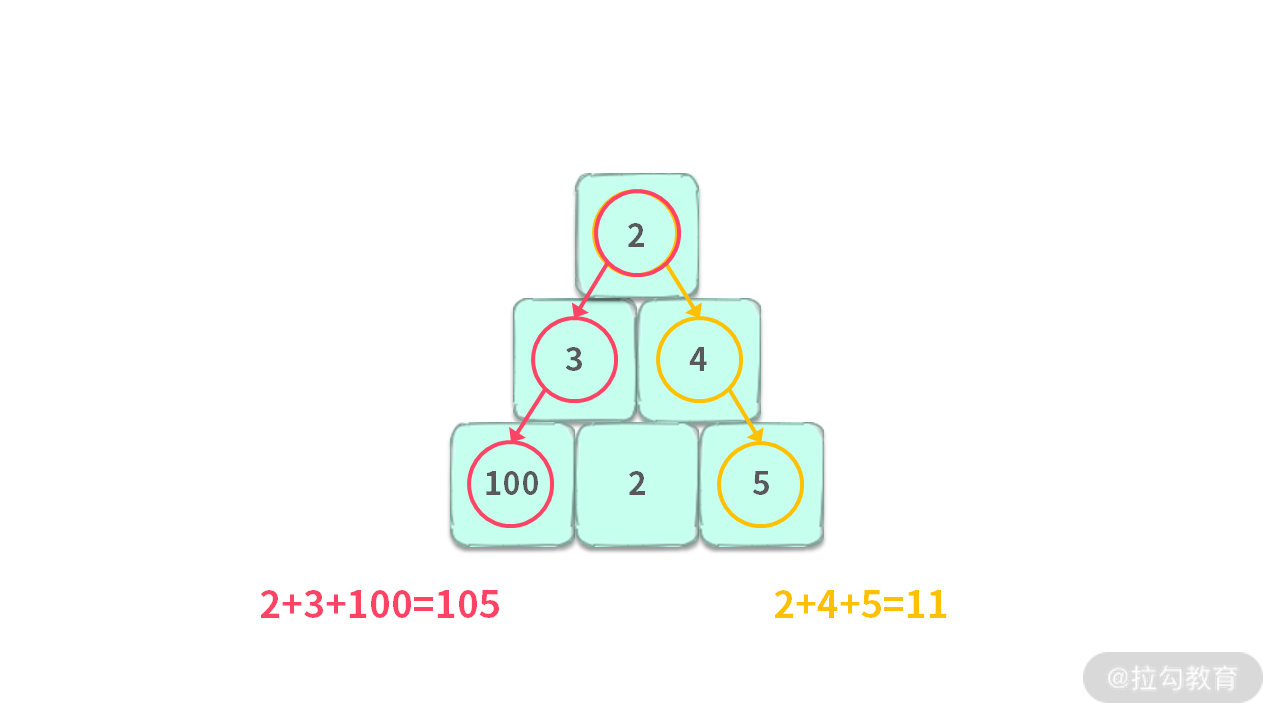
那么问题出在哪里?这是因为在第二层有一个次优解 2 + 3,在第三层能够从 3 跳到 100,最终变成整个问题的最优解。
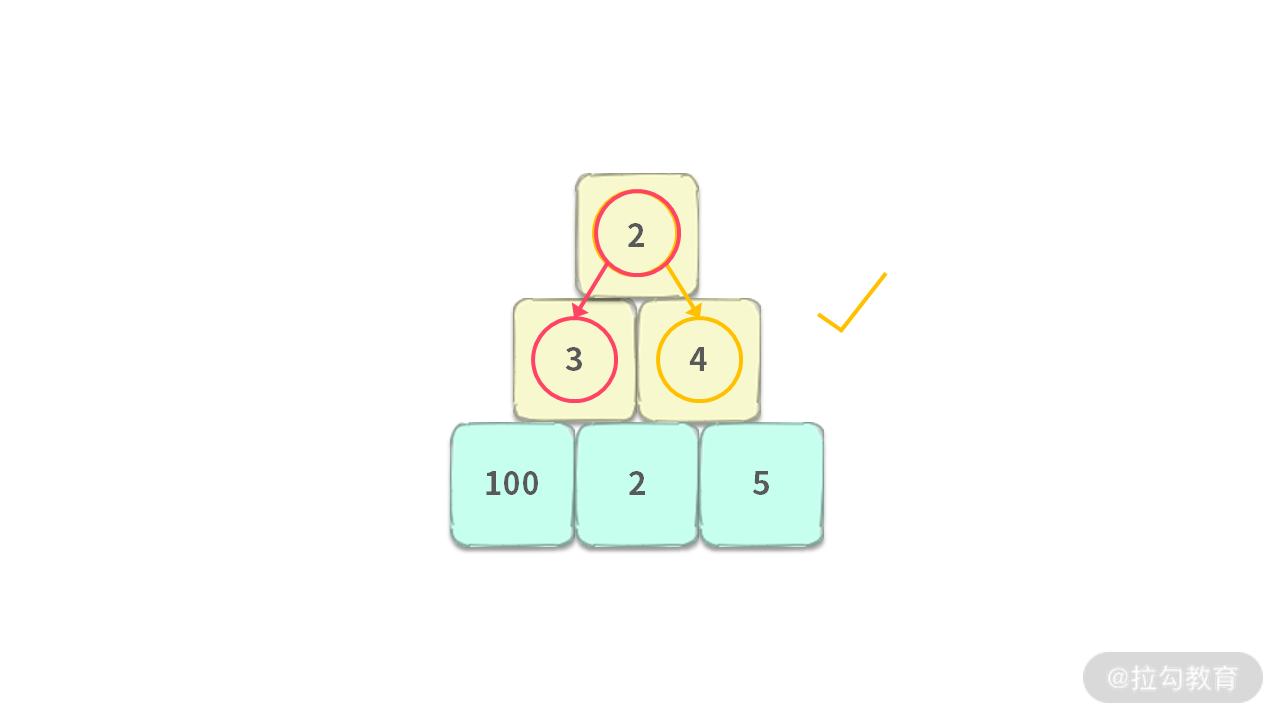
因此,在利用贪心算法的时候,必须要满足 “不能逆袭” 的特性:
局部次优解不能反超,不能成为问题的最终最优解!
注:这里我只是用一个例子来说明 “不能逆袭” 的特性,你能够意会到这种 “次优解反超的特点” 即可。
记忆
在生活中,有一句有趣的歌诀形象地表现了贪心算法的特点:龙生龙,凤生凤,老鼠生儿会打洞。
之前的最优解 “龙” 生成新的 “龙”,依然处在食物链的高层,最后得出的仍然是最优解。而次优解“凤” 和“老鼠”通过繁育是无法完成 “逆袭” 的,因此无法变成最优解。
另外,贪心算法的题目比较依赖一些现有的结论。在日常学习算法和数据结构的过程中,你要特别注意总结经验和积累结论。下面我们一起通过几道例题深入学习贪心算法,然后我还会带你总结出一些有趣的结论。
例 1:木桶装水
【题目】给定一个数组,表示不同的木板的高度,在装水的时候,你可以选择两根木板,然后装满水,在不能倾斜的情况下,里面能装多少水,应该由较短的木板决定。请问最多能装多少水?
输入:A = [1, 0, 1, 1, 0]
输出:3
解释:你可以选择 index = 0 和 index = 3,由于高度都为 1,宽度为 3,装水为 3 x 1 = 3。这样组合装的水最多。
【分析】在正式求解这道题目之前,我们先从一些简单的题目进行展开。比如我们非常熟悉的:求一个数组中的最大值。相信你拿到这道题目就可以开始写代码了:
int getMaxValue(int[] A) {final int N = A == null ? 0 : A.length;int ans = Integer.MIN_VALUE;for (int i = 0; i < N; i++) {ans = Math.max(ans, A[i]);}return ans;}
如果我们仔细观察上述解法,可以发现贪心算法成立的关键在于:贪心的策略保证了在已知求解范围(绿色)区域里面始终是最大的。如下图所示:
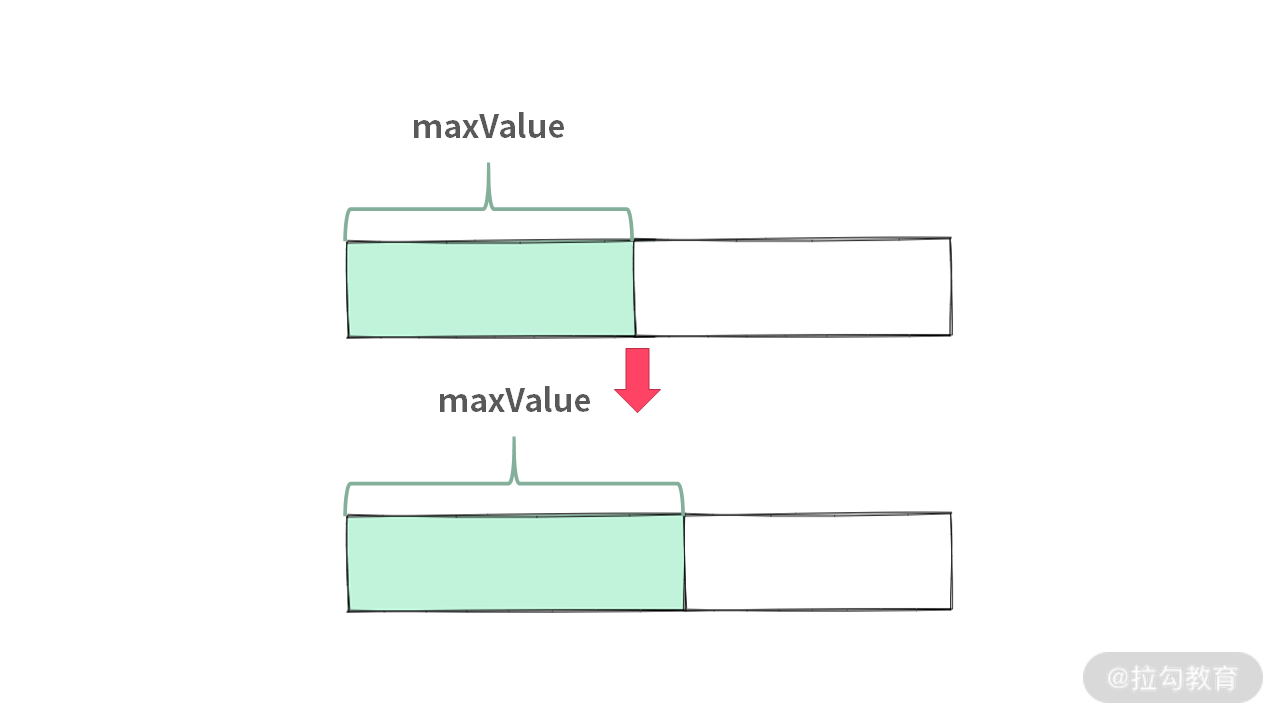
在这个解法里面,我们采用的是从一侧推进来求最大值,如果我问你,是否有其他我们已经学过的办法可以解决这道题目呢?答案就是 “10 | 双指针:如何掌握解决最长,定长,最短区间问题的决窍?” 介绍的双指针。我们可以利用双指针从数组的两侧来推进,求解这个数组的最大值,代码可以写成如下这样:
int getMaxValue(int[] A) {final int N = A == null ? 0 : A.length;int i = 0, j = N - 1;while (i < j) {if (A[i] > A[j]) {j--;} else {i++;}}return A[i];}
如果用比武打个比方,这种思路的依据就是每次取两个人来比武,胜者留下,那么留下来的当然是数组中的最大值。因此,可以得到结论 1。
结论 1:
max(A[i],A[j]) 就是 [0…i] 和 [j … N) 这两个区间里面的最大值。
前面我们都把注意力放在了较大的数。那么,有没有什么结论留给 “较小的数” 呢?
实际上,对于较小的数,还有一个有用的结论。下面我们从头开始推导一下。
首先,数组的最大值所在位置,最终肯定可以将数组切分成 3 个区域,分别用 3 种颜色来表示(如果数组中有多个同值的最大值,只需要挑一个出来当最大值即可)。但是具体如何切分,我们一开始并不清楚。
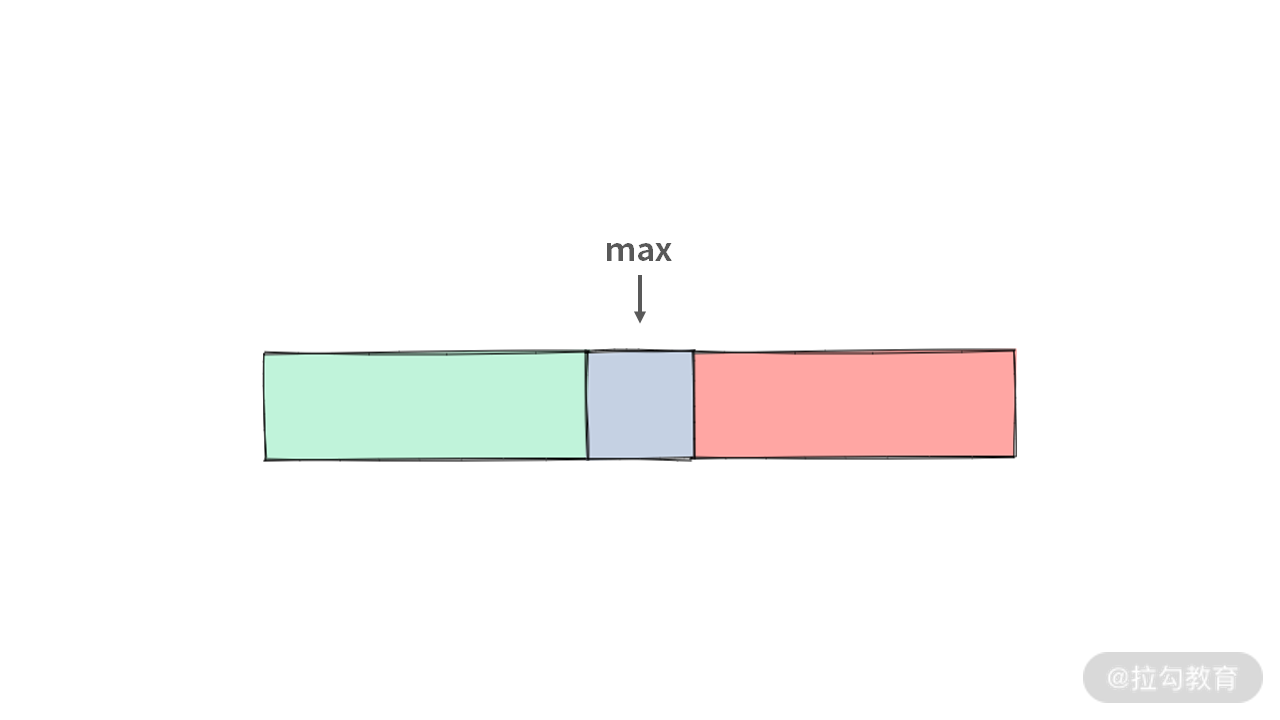
但是,如果利用 i,j 左右同时向中间走,最大值一定出现在 [i, j] 这个范围里面,所以 [0, i) 区域肯定是绿色的,而 (j, N) 区域肯定是红色的。
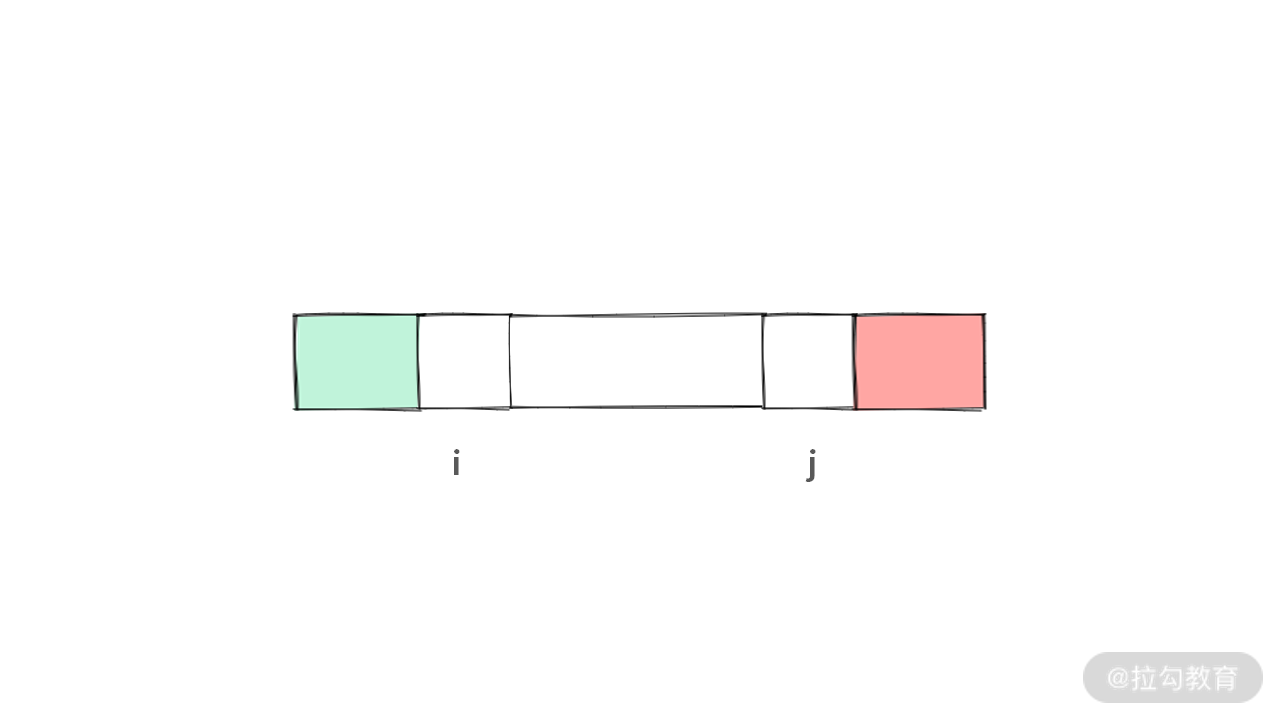
那么,如果 A[i] > A[j],留给较小的数 A[j] 的结论是什么呢?
留下的便是结论 2:
异色区域,大于等于 A[j] 且离 j 最远的元素就是 A[i]。
我们用反证法简略证明一下:假设程序执行到 A[i] > A[j] 成立,但是数组中有另外一个元素 0 <= x < i,并且 A[x] > A[j] 成立。那么:
- 根据结论 1,[0, x] 区域,和 [j, N) 区域里面的最大值必然是 max(A[x], A[j]);
- 由于 A[x] > A[j],所以 [0, x] 区域和 [j, N) 区域里面的最大值必然是 A[x];
- 那么在执行算法的时候,当执行到 A[x] > A[j] 时,会接着执行 j—,也就是说,程序不可能执行到 A[i] > A[j] 位置,这与假设矛盾。
当然,结论 2 也可以针对 A[i] < A[j] 写成:
异色区域,大于等于 A[i] 且离 i 最远的元素就是 A[j]。
那么利用结论 2,我们能做什么呢?由于已经知道异色区域中更大的元素的位置。我们再回到原题,用木板装水的过程中,装水量是由最短的木板决定的。
根据上述分析,我们是不是可以得出第三个结论:装水最多的时候,是否就是异色且成对的
结论 3:
装水最多的时候,必定由异色区域两根木板来装。
但是你可能很快会找到一个反例。如下图所示(注意,不同位置的竖线高度,分别表示相应位置元素的值的大小):
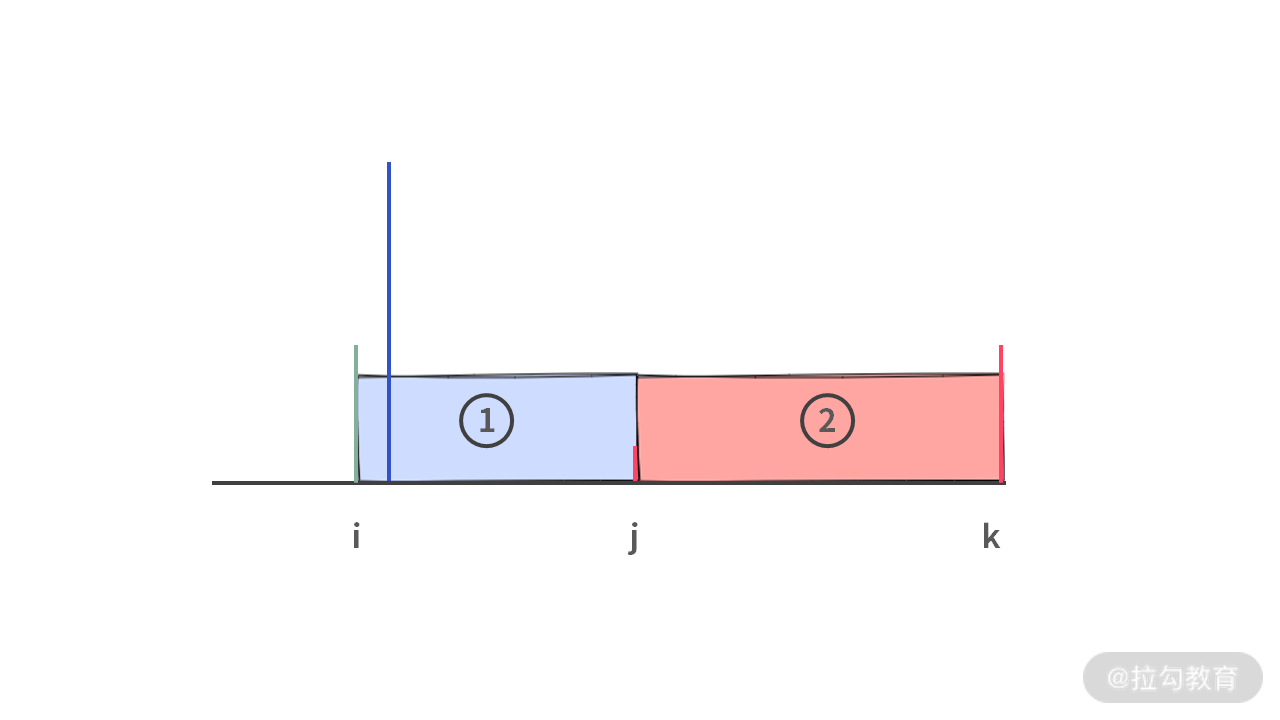
在 j 的同侧,还有一个 A[k] 比 A[j] 稍大且 A[k],A[j] 离得很远。此时 A[i] 和 A[j] 装的水(1 号区域)肯定比 A[j] 和 A[k] 装的水(2 号区域)少。
但是,既然已经出现这种情况,那么可以肯定的是,此时 A[i] > A[j] 且 A[i] > A[k]。并且 A[k] > A[j],实际上可以得到一个更大的装水区域。即由 A[i],A[k] 形成的下图中 3 号区域:
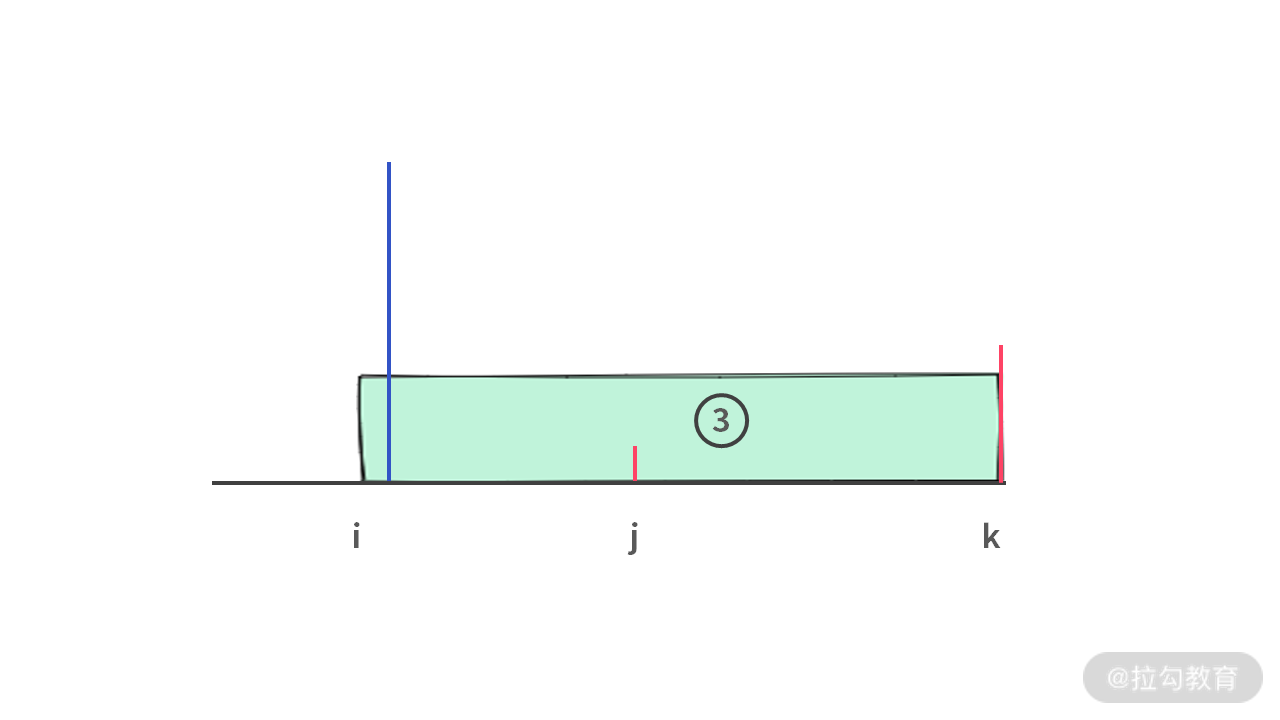
同样也得出结论 3 是成立的。
那么根据结论 3,我们就知道最优答案只能在异色区域里面选(可以想象成装水的水桶两根木板一定要不一样的颜色)。然后根据结论 2,我们又可以知道每个元素 A[x] 在异色区域里面离 x 最远且更大的是谁。那么这道题目就可以求解了。
【代码】根据结论 2 和结论 3 我们可以写出代码如下:
int maxArea(int[] A) {final int N = A == null ? 0 : A.length;int ans = 0;int i = 0, j = N - 1;while (i < j) {int height = Math.min(A[i], A[j]);int width = j - i;ans = Math.max(ans, height * width);if (A[i] > A[j]) {j--;} else {i++;}}return ans;}
复杂度分析:双指针左右同时遍历数组的元素,每个元素只访问一遍,因此,其复杂度为 O(N),空间复杂度为 O(1)。
【小结】本质上这道题就是从 “求一个求数组的最大值” 延伸和演变而来。只是我们通过双指针求解数组最大值的过程中,总结出了结论 1 和结论 2。然后再结合题意要求,得到结论 3,最后使这个问题得到解决。
这道题目的考点我们进行一下归纳。
- 双指针:需要从左右两端向中间走(这和我们前面所讲的双指针略有不同)。
- 贪心算法:通过结论 1、结论 2、结论 3,每一步都选择最优解,最终得到整个问题的最优解。
为了帮助你巩固上述解题方法,这里我再给你留一道类似的题目。
练习题 1:给定一个数组 A[],A[i] 表示柱子的高度,宽度为一个单位。如果我们不停往里面加水,直到所有柱子之间都加满为止。请问:给定一个图形,最多能接多少单位面积的水?
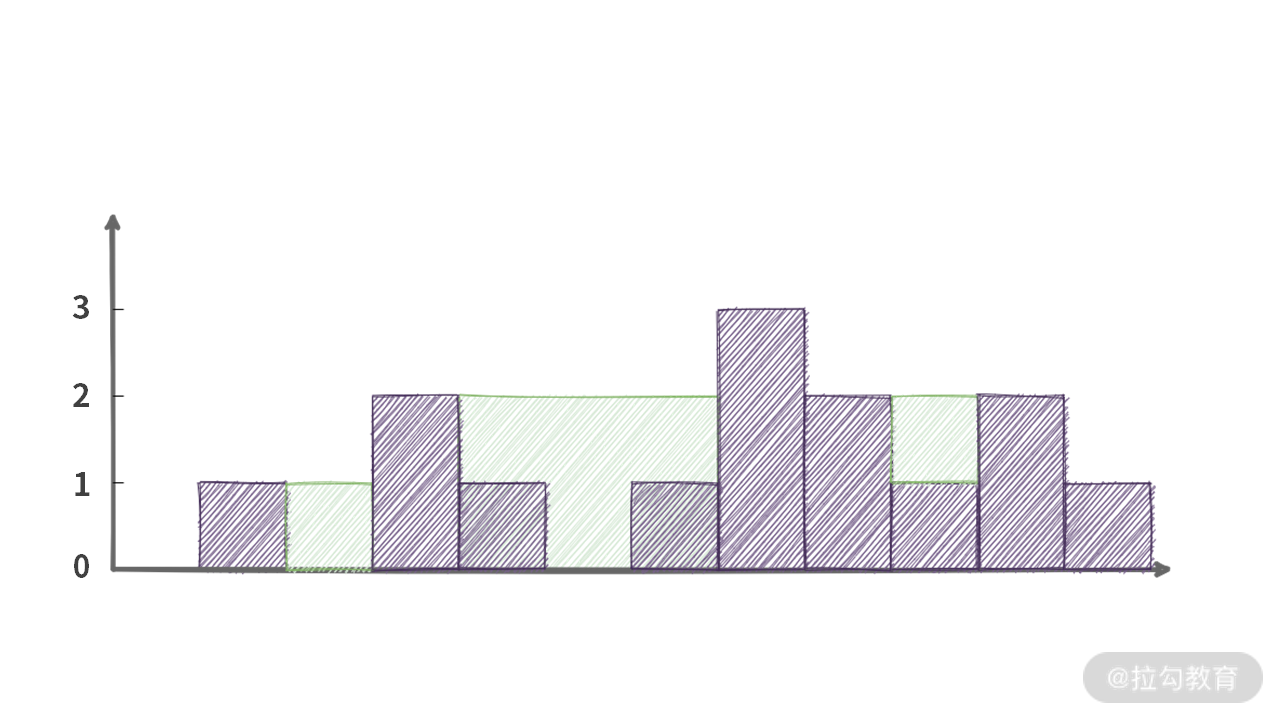
输入:A = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:如图所示,最多只能接 6 个单位面积的水。蓝色部分是水,而黑色部分是柱子,数组中不同的值,由不同高度的柱子表示。
例 2:不重叠区间
【题目】给定一系列区间,请你选一个子集,使得这个子集里面区间都不相互重叠,并且这个子集里面元素个数最多。不重叠的定义:区间 [3,4] 和 [4,5] 就是不重叠。
输入:A = [[1,2],[2, 3], [3,4], [1,3]
输出:3
解释:最多只能选出 3 个区间相互不重叠[1,2], [2,3], [3,4]。
【分析】这个问题,最后相互不重叠的区间应该是初始集合的一个子集。那么,当我们遇到一个区间的时候,应该取还是不取呢?
下面我们从 “单个区间:取和不取” 来展开讲解。这里我们需要稍微进行一下推导。假设:
- 已经求解了下图中的绿色区域,并且得到了绿色区域的最优解 maxNum;
- 接下来我们要处理红色元素(也就是单个的区间)。
(注意:下文的 maxNum 和 newMaxNum 均表示区间里面的不重合区间的最大数目,其中 newMaxNum 表示区间范围变长之后的新的不重合区间的最大数目)
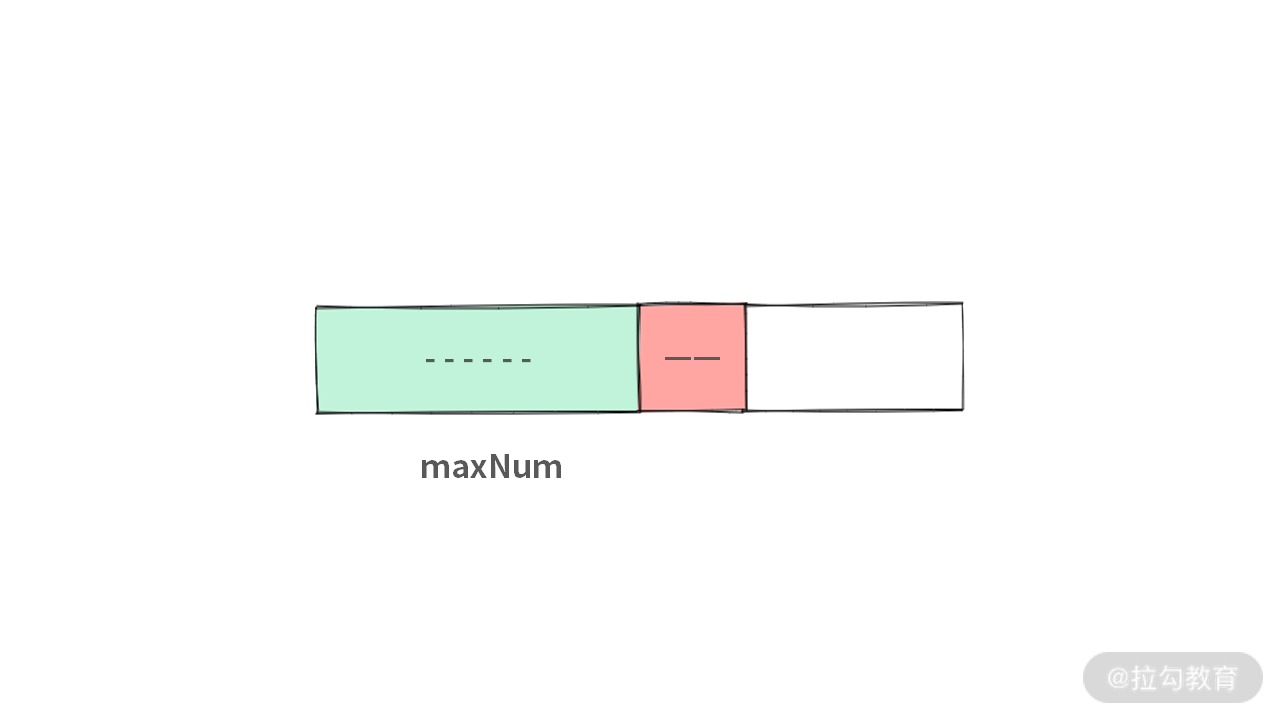
那么当红色区间进来的时候,应该如何更新 maxNum 的值呢?新的 newMaxNum 的值又如何决定呢?
这里可以分为两种情况。
Case 1:newMaxNum 不包含新来的区间(红色部分),应该直接等于旧的 maxNum
Case 2:newMaxNum一定包含新来的区间(红色部分)
如果进行迭代的话,就是:
更新后的最优解 = max(不包含红色区间 =maxNum, 一定包含红色区间的最优解)
Case 1 的值是不需要求解的。那么接下来,我们只需要看 Case 2。
这种情况又可以分为两种小情况。
Case 2.1:新来的区间与旧的任何区间都没有交集,那么 newMaxNum = maxNum + 1。
Case 2.2:新来的区间与旧的区间有交集。
Case 2.1 的值已经计算出来了,我们再来看 Case 2.2。
求解 Case 2.2,需要从区间的不重叠性出发。关于 “区间不重叠”,有一个性质:
两个区间 [a, b] 和 [c,d] 不相交,只需要满足 b <= c || d <= a 就可以了。
现在,我们知道:区间的重叠只需要看两端的大小。可以将绿色区间部分排序。绿色区间集合将分为两部分:
- 集合 a. 与红色新进来的区间有交集(下图紫色部分);
- 集合 b. 与红色新进来的区间没有交集(下图绿色部分)。
我们画图如下:
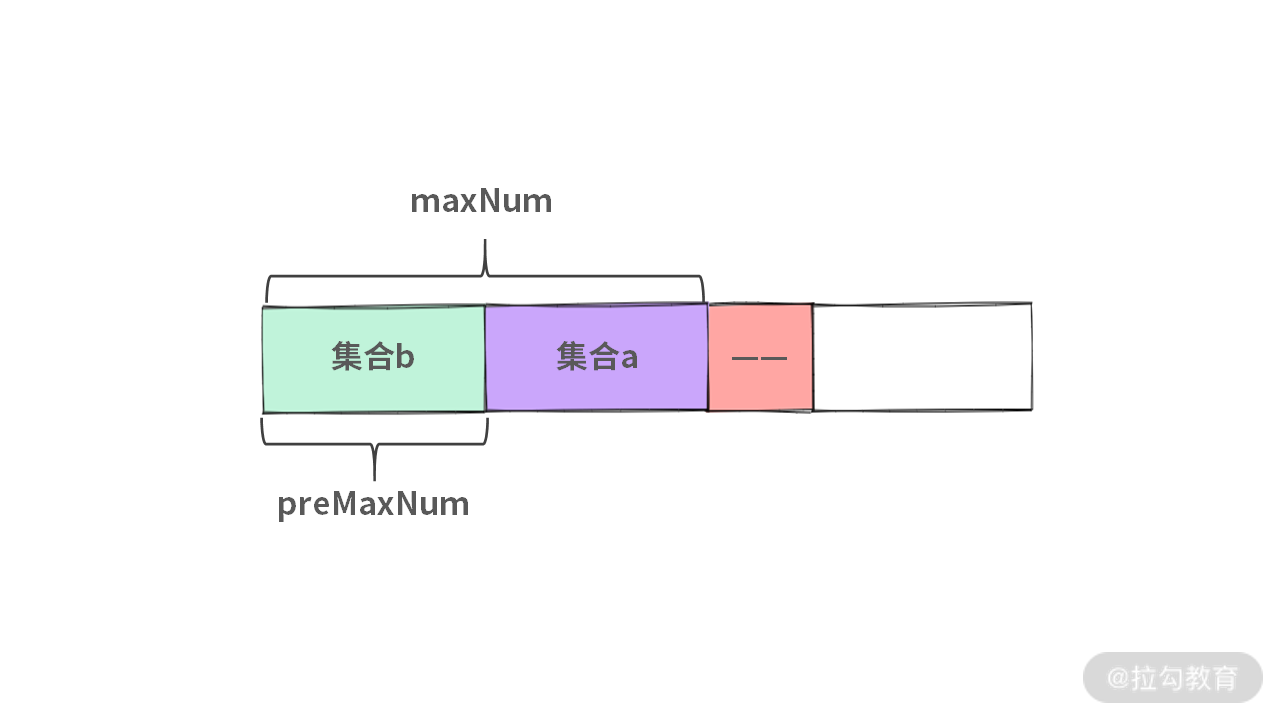
假设已知集合 a 中不重叠的区间个数为 preMaxNum,那么我们就得到了 Case 2.2 的解:preMaxNum + 1。
此外, preMaxNum 肯定小于 maxNum,所以此时 preMaxNum + 1 <= maxNum。也就是说,Case 2.2 最优的时候,都没有 Case 1 好。所以对于整个问题:我们只需要考虑 Case 1 和 Case 2.1。
Case 2.2 逆袭的最优情况也只是等同于 Case 1。次优解不能逆袭超车,正好使用贪心算法。
那么接下来,我们看 Case 1 与 Case 2.1,由此可以得到一个结论 1:
如果新来的区间与前面的区间不重叠,那么不重叠区间数目就能增加一个。
至此,我们知道通过排序,并且依赖性质 1 可以得出两个区间是否重叠。那么如何排序呢?区间有两个端点 [start, end],是按照 start 排序还是按 end 排序呢?
这里我们先用 end 来排序(很多博客上说不能用 start 排序,实际上是可以的,下面我们会具体分析)。
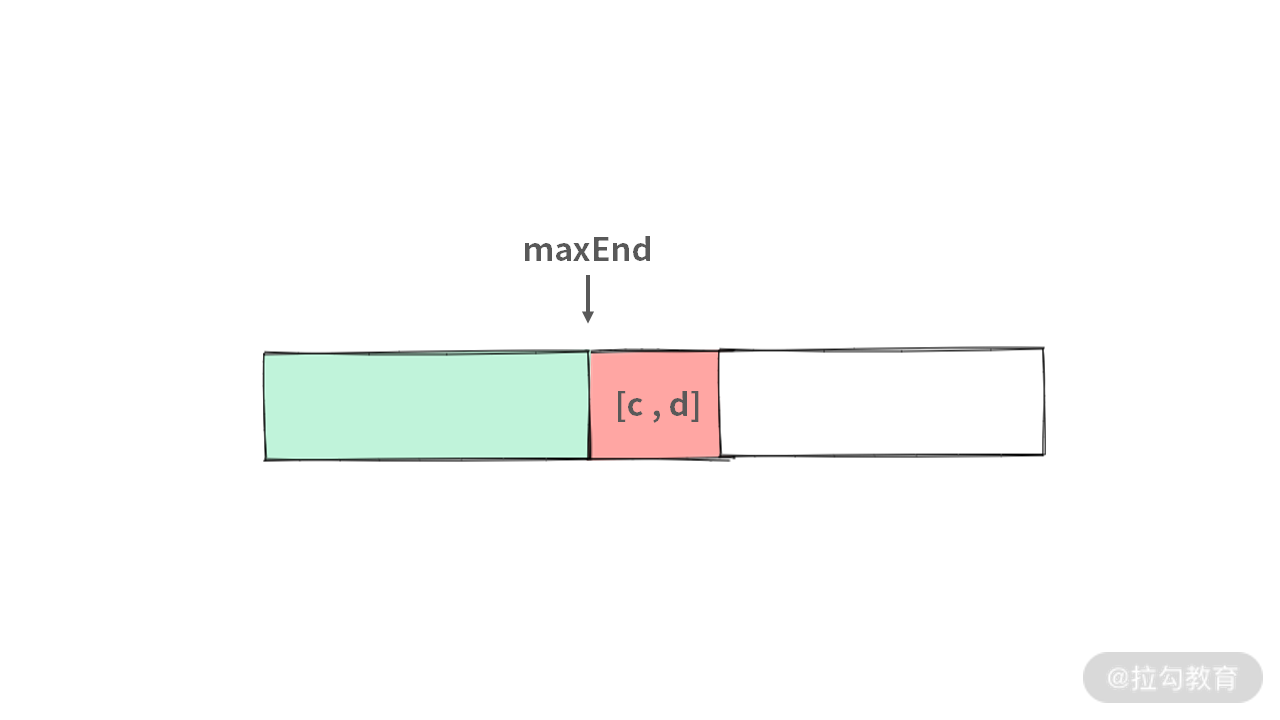
由于我们是按照每个区间的 [start, end] 来排序的,并且用了一个变量 maxEnd 记录已经处理的区间的最大 maxEnd。那么当新区间 [c, d] 进来的时候,只需要判断:
newMaxNum = maxNum + (maxEnd <= c ? 1 : 0);maxNum = newMaxNum;
此外,还需要注意 maxEnd 的更新。在前面的图中,为了简化条件,我并没有清晰地指出 maxEnd 指代的含义。你需要注意 maxEnd 的含义:如果你选取的区间都是不重叠的,maxEnd 是你选中的区间的最大 end,而不是你查看过的区间的最大 end。
因为,只有这样,我们才可以知道要不要把新区间加入不重叠的集合里面。
【代码】原理已经讲清楚了,下面可以开始写代码了(解析在注释里):
int nonOverlapIntervals(int[][] A) {final int N = A == null ? 0 : A.length;Arrays.sort(A, new Comparator<int[]>() {public int compare(int[] a, int[] b) {return a[1] == b[1] ? 0 : (a[1] < b[1] ? -1 : 1);}});int maxEnd = Integer.MIN_VALUE;int ans = 0;for (int i = 0; i < N; i++) {final int start = A[i][0];if (maxEnd <= start) {maxEnd = A[i][1];ans++;}}return ans;}
复杂度分析:假设有 N 个 区间,程序的核心分为排序与贪心。排序的时间复杂度为 O(NlgN),而贪心的算法复杂度为 O(N),空间复杂度为 O(1)。
【小结】我们分析这道题目的时候,并不清楚是否要引入排序,而是一步步推导得出 “需要使用排序来进行预处理”,然后再使用贪心算法。
不过前文说到,排序的时候也可以使用区间 [start, end] 中的 start 排序。这里我就再给出根据 start 进行排序的代码。核心思路:如果在区间排序的时候,根据 start 来排序,那么在处理的时候,需要逆序进行。
int eraseOverlapIntervals(int[][] A) {final int N = A == null ? 0 : A.length;Arrays.sort(A, new Comparator<int[]>() {public int compare(int[] a, int[] b) {return a[0] == b[0] ? 0 : (a[0] < b[0] ? -1 : 1);}});int preStart = Integer.MAX_VALUE;int ans = 0;for (int i = N - 1; i >= 0; i--) {final int start = A[i][0];final int end = A[i][1];if (end <= preStart) {preStart = start;ans++;}}return ans;}
不重叠区间问题是很多问题的模板题。你掌握了这个模板就可以解决掉更多题目。下面请你尝试完成下面一批练习题。你一定要自己动手练习,不要偷懒哦!如果有你对哪里有疑问,也欢迎你写在留言区,我们一起讨论。
练习题 2:给定一系列区间,返回最少需要删除的区间数目,使得剩下的区间不重叠。
输入:A = [[1,2], [2,3], [1,4]]
输出:1
解释:这里我们选择删除 [1, 4] 剩下的区间便不再重叠。这是最少的删除区间的数目。
练习题 3:给定一个字符串,需要切分成尽可能多的切片,但是一个字母只能放在一个切片里面。
输入:A = “abcabdefg”
输出:5
解释:最多可以分为 [“abcab” “d” “e” “f” “g”]。你不能切成 [“a”, “b”, “c”, “a”, “b”, “d”, “e”, “f”, “g”],在这种情况下’a’ 字母并没有处于同一个切片。
练习题 4:给定一系列区间,将重合的区间合并在一起。
输入:A = [[1,2], [2,3], [2,6], [7, 8]]
输出:[[1, 6], [7,8]]
例 3:青蛙跳
【题目】给定一个数组 A[],元素 A[i] >= 0,一只青蛙站在 index = i,那它可以跳到 A[i+1], …, A[i+A[i]](当然,它是不能跳出数组的)。那么请问这只青蛙从 index = 0 出发,能不能跳到 index = A.length - 1。
输入:A = [2, 3, 1, 2, 1]
输出:true
解释:青蛙可以这样跳,A[0] → A[1] → A[4]
【分析】这个问题的重点在于,站在 index = i,那它可以跳到 [i, …, i + A[i]]。
因此,它表示的信息就是两点:
- 起点 i
- 终点 i + A[i]
这货不就是一个区间吗?因此,数组里面的每一个元素,实际上都表示了一段区间 [i, i + A[i]]。并且,这些区间都已经按照区间的起始点排好序了。
那么问题就演变成:给定一系列区间,这段区间是否可以连续覆盖 [0, N-1] 这个范围。题目也就变成一个区间覆盖问题。
当走到位置 i 的时候,相当于已经覆盖了范围 [0, i + A[i]]。那么接下来,由于我们需要实现的目标是:连续覆盖得越远越好。
因此只需要选择这样的区间:
- 区间的起始位置 x 一定要在 [0, i + A[i]] 范围里面,也就是要满足相连;
- 区间的终止位置 x + A[x] 一定要越远越好。
那么,我们可以写出暴力的算法版本 1如下:
class Solution {public boolean canJump(int[] A) {final int N = A == null ? 0 : A.length;int coveredRange = A[0];int used = 1;while (coveredRange < N - 1 && used < N) {int oldCoveredRange = coveredRange;for (int i = 0; i < N; i++) {if (i <= oldCoveredRange) {if (i + A[i] > coveredRange) {coveredRange = i + A[i];}}}if (oldCoveredRange == coveredRange) {return false;}used++;}return true;}}
暴力算法每次在完成区间更新的时候,都是搜索所有可能的解,因此其正确性是可以得到保证的。(在测试平台上也可以通过)。但是面试官要的肯定不是复杂度这么高的算法。因此,我们需要在此基础上继续优化。
【优化 1】由于连续性的要求,在扫描的时候,不需要遍历 [0, N) 的所有元素,只需要遍历 [0,oldCoveredRange] 这个范围里面的元素。那么扫描循环可以优化如下:
for (int i = 0; i <= oldCoveredRange; i++) {if (i + A[i] > coveredRange) {coveredRange = i + A[i];}}
【优化 2】我们发现:
- 如果有区间在覆盖范围 [0, A] 里面被扫描过了;
- 在下一轮覆盖范围 [0, B] 里面还会被扫描;
- B >= A。
而 [0, B] 实际上可以分为两段,[0, A] 和 [A+1, B]。既然 [0,A] 这一段已经扫描过了,那么为了避免重复扫描,接下来只需要扫描 [A+1, B] 即可。因此,每次扫描的时候,你都需要记住当前这次扫描的终点 A。
【代码】根据上述分析,我们就可以写出如下代码了(解析在注释里):
class Solution {public boolean canJump(int[] A) {final int N = A == null ? 0 : A.length;int preScanedPos = -1;int curCoveredRange = 0;while (curCoveredRange < N - 1) {int oldCoveredRange = curCoveredRange;for (int i = preScanedPos + 1;i <= oldCoveredRange; i++) {if (i + A[i] > curCoveredRange) {curCoveredRange = i + A[i];}}if (oldCoveredRange == curCoveredRange) {return false;}preScanedPos = oldCoveredRange;}return true;}}
复杂度分析:时间复杂度 O(N),空间复杂度 O(1)。实际上,这里最多每个点遍历一次,所以时间复杂度为 O(N)。
【小结】在做完这个题之后,不妨和我们 “第 02 讲” 学过的 FIFO 队列进行一个知识上的联动。
记得我以前学习队列的时候,访问一个点时,会把后续的点都放到队列中,如下图所示:
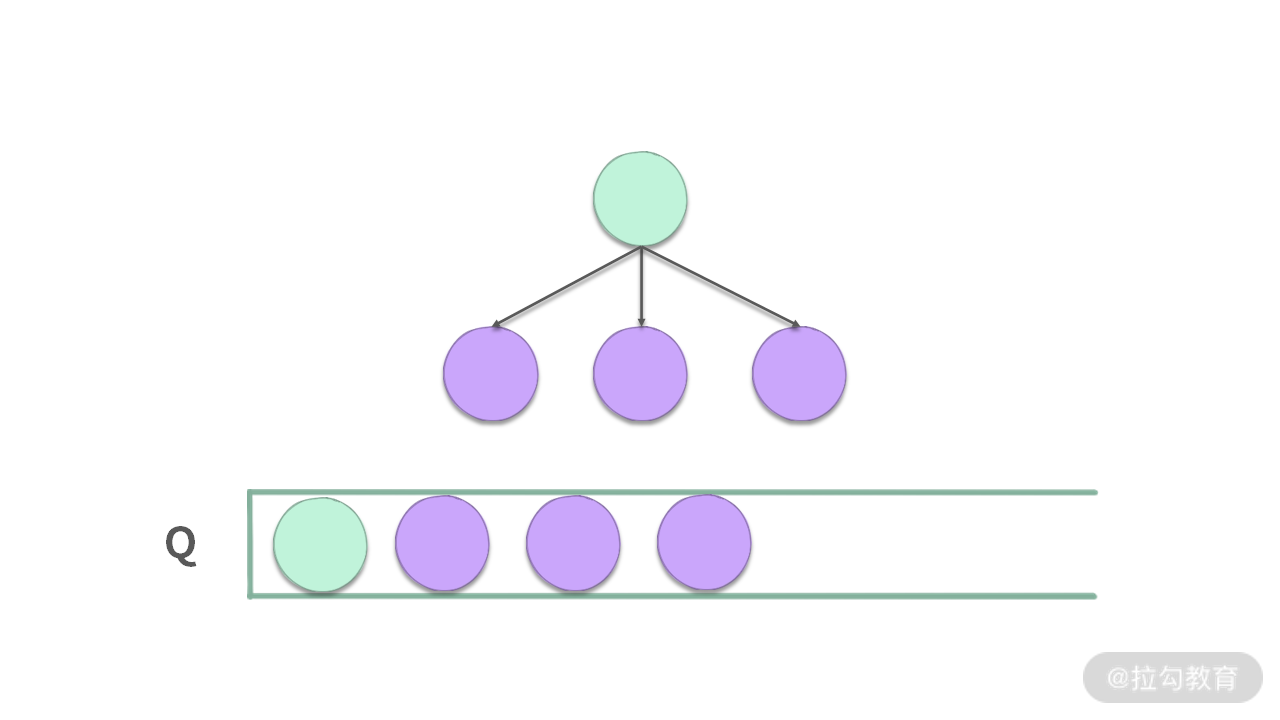
但是在这道题中,当访问 i 这个点的时候,后续能够走的点是 A[i+1] … A[i+A[i]],但并没有把所有的点都入队,而是从里面选择了一个最优的点。
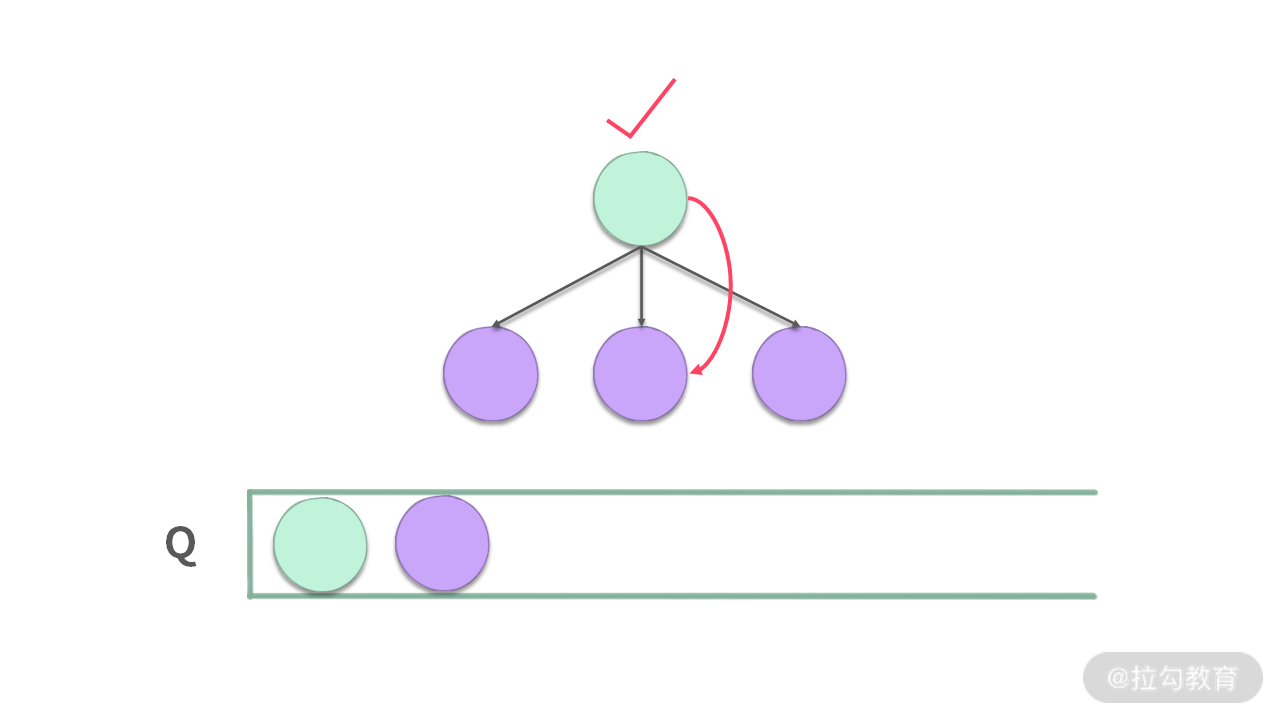
如果把遍历的顺序也放到一个队列中,那么入队的时候,就只是把后面最优的点放到队列中。这个性质和优先级队列不太一样。优先级队列会把所有的元素都放到堆里面,然后堆内有序。但是对于贪心来说,只需要把最优秀的元素入队即可。
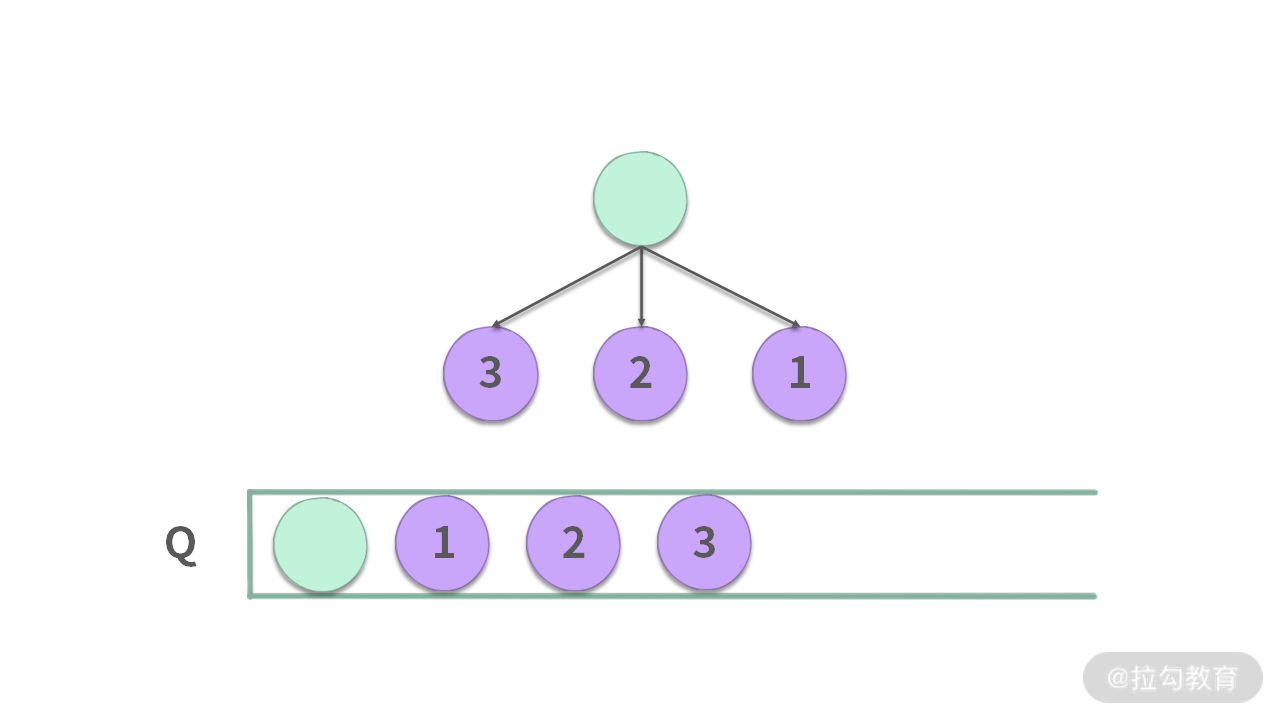
当然,由于每次都只选一个后续最优元素入队,因此这个 Queue 的长度最长是 1。这和我们之前学过的队列知识存在相似之处,但也有不同的地方。
如果我们再从深度上挖掘一下这道题,还可以有得到下面这些练习题。
练习题 5:问题与例 3 一样,只不过这个题:需要输出最少跳跃的次数?如果不能跳到 A.length-1,请输出 -1。
输入:A = [2, 3, 1, 2, 1]
输出:2
解释:A[0]→A[1]→A[4] 最少跳两次就可以到达最后一个下标。
接下来我们看一下:给定一系列区间,如果要完全覆盖 [start, end] 这个区间,应该如何处理呢?请看练习题 6。
练习题 6:一个大门安装了好几个摄像头,每个摄像头会录下一段时间的视频(假设起始时间与结束时间都是一个整数,可能为负数)。如果想找到 [0, T] 时间段的视频,请问最少需要提取几个摄像头的视频?如果不能得到 [0, T] 这个时间段的视频,输出 -1。
输入:[[1,2], [0,2], [0,1], [2,3], [2,6], [3,8]], T = 5
输出:2
解释:只需要用 [0, 2],[2,6] 就可以完全覆盖 [0, 5] 这个时间段。因此,最少需要看 2 个摄像头。
例 4: 加油站
【题目】巨大的环形赛道上有 N 个加油站,第 i 个加油站可以加油 G[i] 升,而从第 i 个加油站开到下一个加油站,需要 C[i] 升汽油。请你选择一个起始加油站,能够跑完环形赛道一圈。
条件:1. 注意是环形赛道;2. 汽车油箱总是足够大。
输入:G = [1,2], C=[2, 1]
输出:1
解释:从站点 0 出发,一开始只能收获 1 升油,而从 index = 0 跑到 index = 1 需要用掉 2 升汽油,所以不能从站点 0 出发。而从站点 1 出发,则可以绕着环形跑道跑一圈。
【分析】当拿到这个题的时候,我们首先考虑一种极端情况,那就是收入与付出不成正比。当 sum(G) < sum(C) 的时候,应该是无论如何也不可能跑一圈的。
那么接下来就只需要考虑 sum(G) >= sum(C) 的情况。在这种情况下,可以得到结论 1:
当 sum(G) >= sum(C) 时,必然存在某个点出发可以绕着赛道跑一圈的情况。
证明这个结论需要使用反证法。假设:当 sum(G) >= sum(C),不存在某个点出发,可以绕着赛道跑一圈。若假设成立,那么必然可以将环形跑道切成几段,如下图所示:
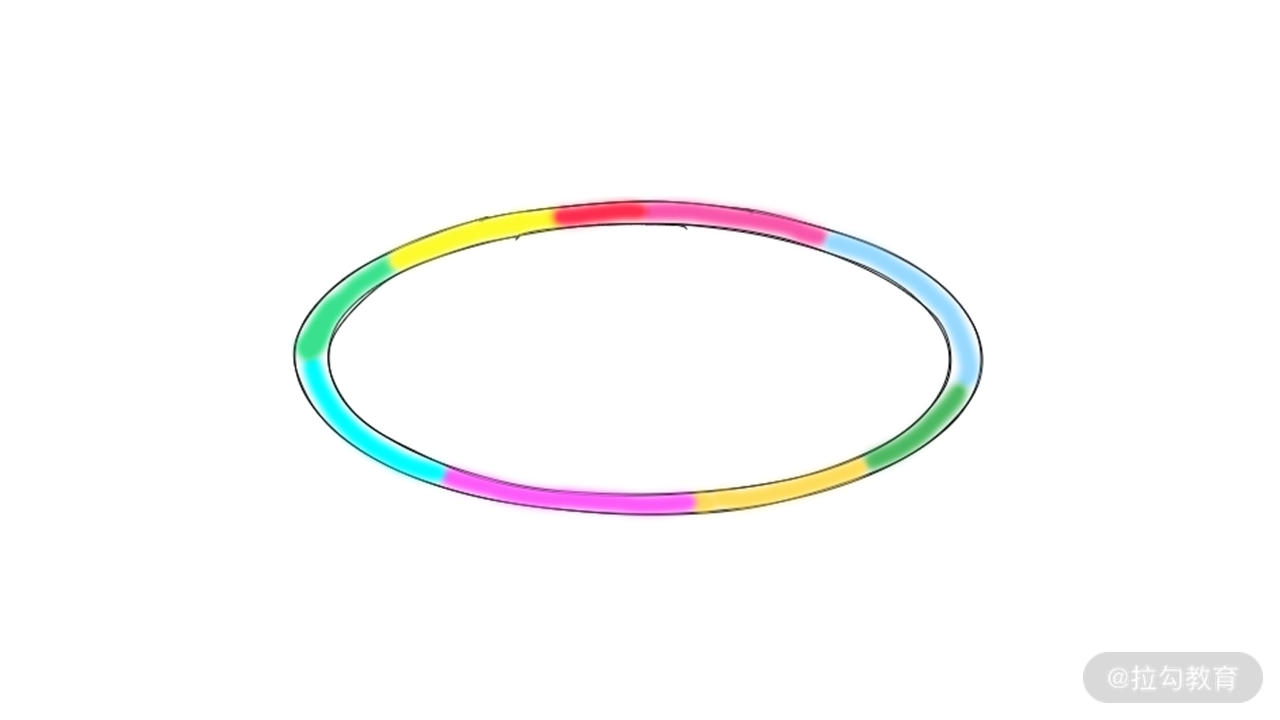
并且每一段都是负数(因为不能绕着跑道跑一圈)。这时不同的段用不同的颜色表示。由于每一个小段和都是 sub_sum(G) < sub_sum(C),那么必然可以得到总和 sum(G) < sum(C)。这与题目条件相矛盾。
注:我们用 sub_sum() 函数表示求这一小段对应子数组的和。
根据结论 1,可以将 sum(G) >= sum(C) 的情况再次分为两种。
- Case 1:从站点 0 出发可以跑遍全场。
- Case 2:从非 0 站点出发可以跑遍全场。
如果是 Case 1,那么我们可以写出代码如下(解析在注释里):
int ans = 0;int left = 0;for (int i = 0; i < N; i++) {total += G[i] - C[i];if (left + G[i] - C[i] >= 0) {left += G[i] - C[i];} else {}}return ans;
如果是 Case 2,接下来我们再看一下不能从站点 0 出发的情况。也就是存在某个点 i,使得汽油不够了。会有 left(余下的汽油) + G[i] - C[i] < 0,那接下来应该从哪里开始呢?
- 首先,当 G[0] - C[0] < 0 的时候,肯定是不能从 0 开始。
- 其次,当 G[0] - C[0] >= 0 的时候,如果 [0, i] 的油量收益为负数。那么中间任意选一个点 x,且 0 < x <= i,那么 [x, i] 这个区间上的油量收益也必然为负(因为去掉了从 0 位置出发的正收益 G[0] - C[0])。
这两种情况可以统一处理如下:当出现油量不够的时候,下一个尝试的起点应该是 i + 1。
此时我们可以统一用代码处理如下(解析在注释里):
int ans = 0;int left = 0;int total = 0;for (int i = 0; i < N; i++) {total += G[i] - C[i];if (left + G[i] - C[i] >= 0) {left += G[i] - C[i];} else {ans = i + 1;left = 0;}}return total < 0 ? -1 : ans;
但是需要验证找到的 ans 站点出发,可以绕赛道一圈?答案是不需要的,下面我们证明一下这个结论。
假设从 ans=start 站点出发,那么环形区域必然可以分为两半部分,[0, start) 和 [start, N)。由于不能从 index = 0 出发,那么 [0, start) 这个区域油量收益肯定是 sub_sum(G) < sub_sum(C),即油量收益肯定是负数。
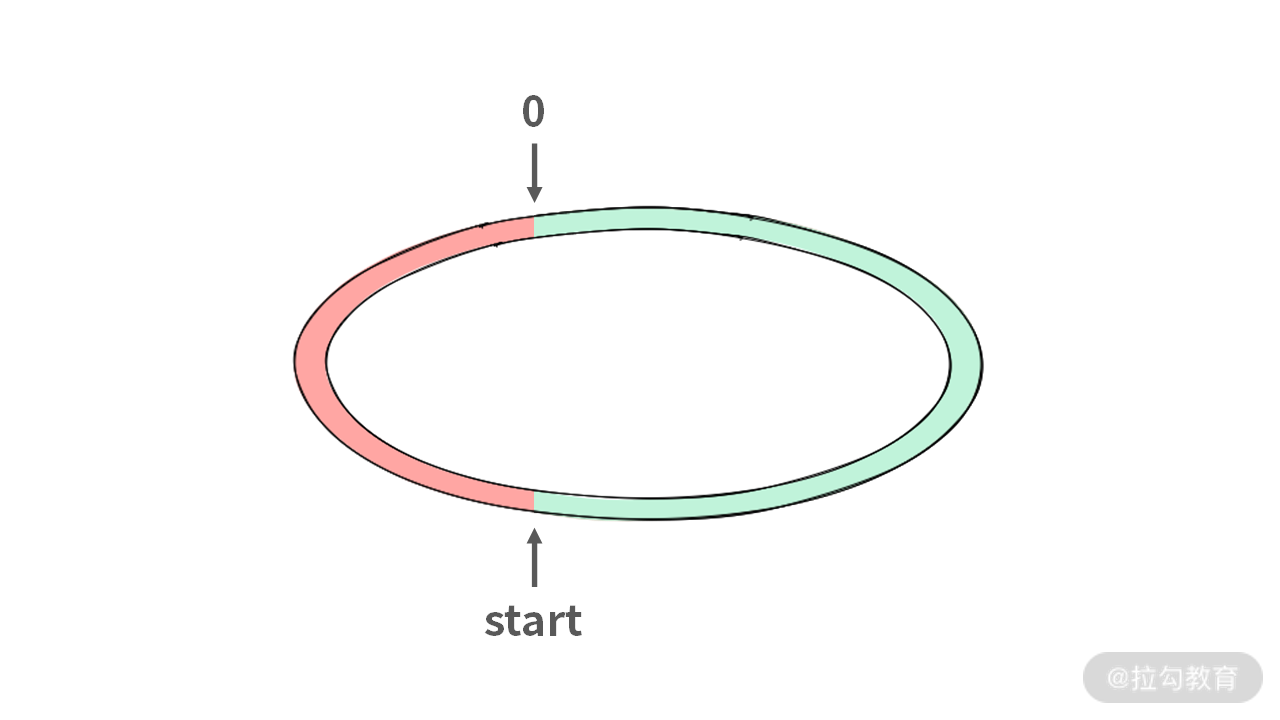
由于油的总量是 sum(G) >= sum(C),那么后半段油的收益 sub_sum(G) - sub_sum(C) > 0 必然成立。并且,我们可以得到:后半段的收益肯定可以平衡掉前半段的负收益。因此,从 start 出发,就必然可以绕着赛道跑一圈。
【代码】到此时,我们已经可以写出代码了(解析在注释里):
int canCompleteCircuit(int[] G, int[] C) {final int N = G == null ? 0 : G.length;long left = 0;int ans = 0;long total = 0;for (int i = 0; i < N; i++) {final int get = G[i];final int cost = C[i];total += get - cost;if (left + get - cost >= 0) {left += get - cost;} else {left = 0;ans = i + 1;}}return total >= 0 ? ans : -1;}
复杂度分析:时间复杂度为 O(N),空间复杂度为 O(1)。
【小结】我们经过层层分析,得到最终求解的代码。最后还证明了不需要额外的代码去验证 ans 站点出发的有效性。在这个题中用到的结论 1 是我们分析问题的关键。
不过这个题还有一个比较有趣的解法,解题思路是这样的:
- 当总和小于 0 的时候,肯定没有解;
- 当总和大于等于 0 的时候,总是有解的,那么在选择起点的时候,可以选择一个子数组,这个子数组是数组里面的最大和,然后就以这里作为起点。(可以反证一下,如果从最大子数组和的起点出发都不能绕赛道一圈,那么其他的点就更没戏了)。
不过想要通关这种解法,需要你依次解决以下几道练习题哦。
练习题 7:给定一个数组,求这个子数组里面的最大子数组和。
输入:A = [1,-5,3,4]
输出:7
解释:最大子数组和为 [3,4],形成的和为 7,没有比 7 更大的子数组和了。
练习题 8:给定一个数组,这个数组首尾成环,求这个环形数组里面的最大子数组和。
输入:A = [2, -2, -2, -2, 2]
输出:4
解释:最大子数组为首尾的 [2, 2],形成的和为 4,没有比 4 更大的子数组和了。
练习题 9:同样是例题 4,你能使用我们前面提过的 “从最大子数组和的起点出发” 这种思路进行求解吗?
总结与延伸
贪心算法是一种思路,没有模板和套路。不过经过今天的学习。可以发现,贪心算法的两个特点中,第一个特点只选局部最优解是比较容易做到的。但是难点在于: 次优解不能逆袭。
往往我们要花非常多的时间证明,才能够保证次优解可以扔掉。这里面还涉及了非常多的数学思维,需要你活学活用。
作为面试官,我给你的建议是:刷贪心题目的时候,一定要注意推导!如果你不会证明:“为什么次优解可以扔掉?”,但知道如何进行操作,这说明你还没有真正掌握贪心这种思想。
思考题
最后我再给你留一道思考题:既然可以用练习题 8 思路解决例 4 的问题,那么肯定也可以用例 4 的思路解决练习题 8,你能想一下代码应该怎么写吗?
给定一个数组,这个数组首尾成环,求这个环形子数组里面的最大子数组和。
输入:A = [2, -2, -2, -2, 2]
输出:4
解释:最大子数组为首尾的 [2, 2],形成的和为 4,没有比 4 更大的子数组和了。
希望你可以自己动一动手,也欢迎在留言区分享你的思路,我们一起讨论。接下来请和我一起踏上更加奇妙的算法旅程,下一讲将介绍 12 | 回溯:我把回溯总结成一个公式,回溯题一出就用它。记得按时来探险。

