21 | 如何利用 JavaScript 实现经典数据结构？

前端基础建设与架构 - 前百度资深前端开发工程师 - 拉勾教育

前面几讲我们从编程思维的角度分析了软件设计哲学。从这一讲开始，我们将深入数据结构这个话题。

数据结构是计算机中组织和存储数据的特定方式，它的目的是方便且高效地对数据进行访问和修改。数据结构体现了数据之间的关系，以及操作数据的一系列方法。数据又是程序的基本单元，因此无论哪种语言、哪种领域，都离不开数据结构；另一方面，数据结构是算法的基础，其本身也包含了算法的部分内容。也就是说，想要掌握算法，有一个坚固的数据结构基础是必要条件。

下面我们用 JavaScript 实现几个常见的数据结构。

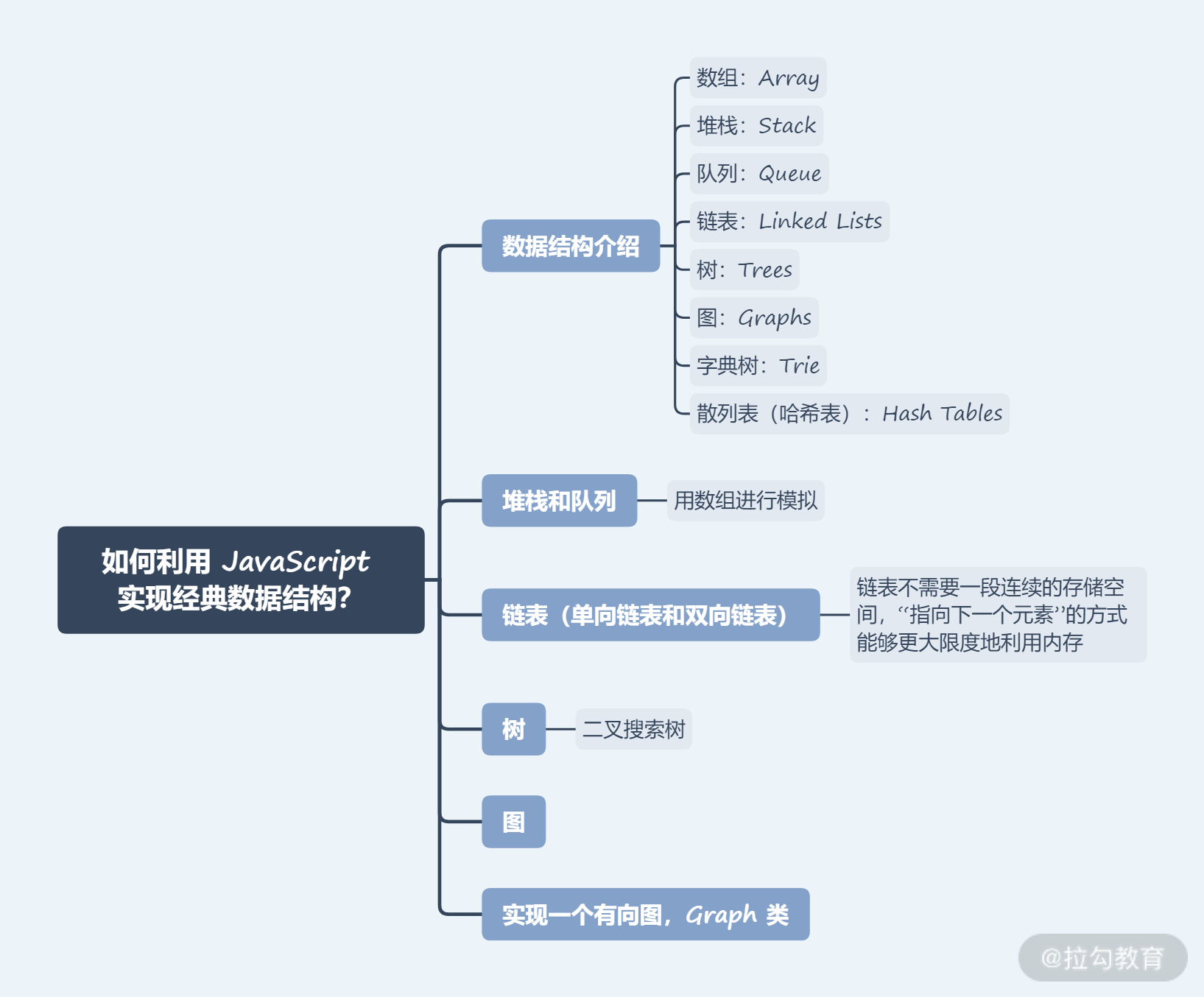
数据结构介绍

我通常将数据结构分为八大类。

• 数组：Array
• 堆栈：Stack
• 队列：Queue
• 链表：Linked Lists
• 树：Trees
• 图：Graphs
• 字典树：Trie
• 散列表（哈希表）：Hash Tables

我们可以先大体感知一下各种数据结构之间的关系：

• 栈和队列是类似数组的结构，非常多的初级题目要求用数组实现栈和队列，它们在插入和删除的方式上和数组有所差异，但是实现还是非常简单的；
• 链表、树和图这种数据结构的特点是，其节点需要引用其他节点，因此在增 / 删时，需要注意对相关前驱和后继节点的影响；
• 可以从堆栈和队列出发，构建出链表；
• 树和图最为复杂，但它们本质上扩展了链表的概念；
• 散列表的关键是理解散列函数，明白依赖散列函数实现保存和定位数据的过程；
• 直观上认为，链表适合记录和存储数据；哈希表和字典树在检索数据以及搜索方面有更大的应用场景。

以上这些 “直观感性” 的认知并不是“恒等式”，我们将在下面的学习中去印证这些“认知”，这两讲中，你将会看到熟悉的 React、Vue 框架的部分实现，将会看到典型的算法场景，也请你做好相关基础知识的储备。

堆栈和队列

栈和队列是一种操作受限的线性结构，它们非常简单，虽然 JavaScript 并没有原生内置这样的数据结构，但是我们可以轻松地模拟出来。

栈的实现，后进先出 LIFO（Last in、First out）：

class Stack {
  constructor(...args) {
this.stack = [...args]
  }
  push(...items) {
return this.stack.push(... items)
  }
  pop() {
return this.stack.pop()
  }
  peek() {
return this.isEmpty() 
        ? undefined
        : this.stack[this.size() - 1]
  }
  isEmpty() {
return this.size() == 0
  }
  size() {
return this.stack.length
  }
}

队列的实现，先进先出 FIFO（First in、First out），“比葫芦画瓢” 即可：

class Queue {
  constructor(...args) {
this.queue = [...args]
  }
  enqueue(...items) {
return this.queue.push(... items)
  }
  dequeue() {
return this.queue.shift()
  }
  front() { 
return this.isEmpty()
        ? undefined
        : this.queue[0]
  }
  back() {
return this.isEmpty()
        ? undefined
        : this.queue[this.size() - 1]
  }
  isEmpty() {
return this.size() == 0
  }
  size() {
return this.queue.length
  }
}

我们可以看到不管是栈还是队列，都是用数组进行模拟的。数组是最基本的数据结构，但是它的价值是惊人的。我们会在下一讲，进一步介绍栈和队列的应用场景。

链表（单向链表和双向链表）

堆栈和队列都可以利用数组实现，链表和数组一样，也实现了按照一定的顺序存储元素，不同的地方在于链表不能像数组一样通过下标访问，而是每一个元素都能够通过 “指针” 指向下一个元素。我们可以直观地得出结论：链表不需要一段连续的存储空间，“指向下一个元素” 的方式能够更大限度地利用内存。

根据上述内容，我们可以总结出链表的优点在于：

• 链表的插入和删除操作的时间复杂度是常数级的，我们只需要改变相关节点的指针指向即可；
• 链表可以像数组一样顺序访问，查找元素的时间复杂度是线性的。

要想实现链表，我们需要先对链表进行分类，常见的有单链表和双向链表。

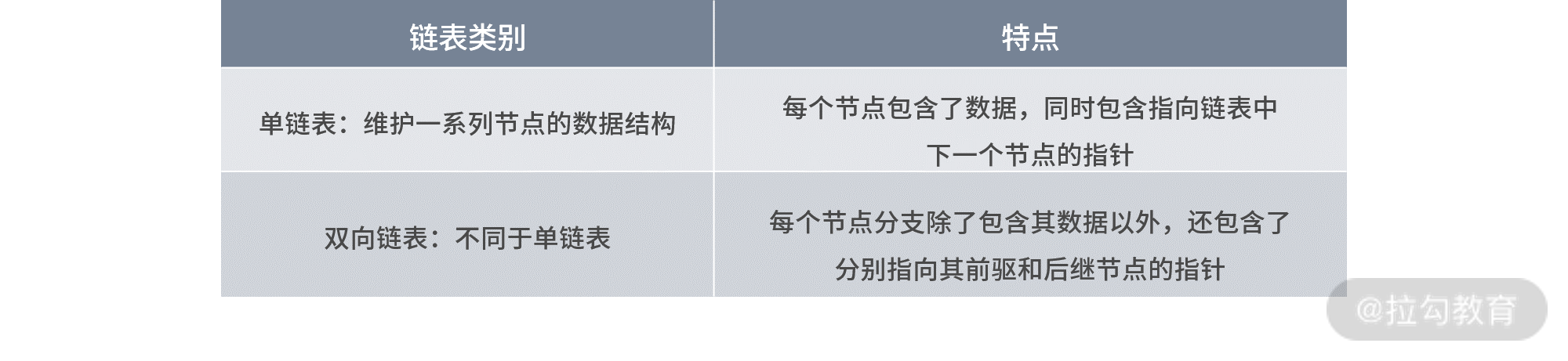
• 单链表：单链表是维护一系列节点的数据结构，其特点是：每个节点包含了数据，同时包含指向链表中下一个节点的指针。
• 双向链表：不同于单链表，双向链表特点：每个节点分支除了包含其数据以外，还包含了分别指向其前驱和后继节点的指针。

首先，根据双向链表的特点，我们实现一个节点构造函数（节点类），如下代码：

class Node {
    constructor(data) {
this.data = data
this.next = null
this.prev = null
    }
}

有了节点类，我们来初步实现双向链表类，如下代码：

class DoublyLinkedList {
    constructor() {
this.head = null
this.tail = null
    }
}

接下来，需要实现双向链表原型上的一些方法，这些方法包括以下几种。

• add：在链表尾部添加一个新的节点，实现如下代码：

add(item) {
  let node = new Node(item)
if(!this.head) {
this.head = node
this.tail = node
  }
else {
    node.prev = this.tail
this.tail.next = node
this.tail = node
  }
}

• addAt：在链表指定位置添加一个新的节点，实现如下代码：

addAt(index, item) {
   let current = this.head
   let counter = 1
   let node = new Node(item)
if (index === 0) {
this.head.prev = node
     node.next = this.head
this.head = node
   } 
else {
while(current) {
      current = current.next
if( counter === index) {
        node.prev = current.prev
        current.prev.next = node
        node.next = current
        current.prev = node
      }
      counter++
    }
  }
}

• remove：删除链表指定数据项节点，实现如下代码：

remove(item) {
  let current = this.head
while (current) {
if (current.data === item ) {
if (current == this.head && current == this.tail) {
this.head = null
this.tail = null
      } 
else if (current == this.head ) {
this.head = this.head.next
this.head.prev = null
      } 
else if (current == this.tail ) {
this.tail = this.tail.prev;
this.tail.next = null;
      } 
else {
        current.prev.next = current.next;
        current.next.prev = current.prev;
      }
   }
   current = current.next
  }
}

• removeAt：删除链表指定位置节点，实现如下代码：

removeAt(index) {
  let current = this.head
  let counter = 1
if (index === 0 ) {
this.head = this.head.next
this.head.prev = null
  } 
else {
while(current) {
    current = current.next
if (current == this.tail) {
this.tail = this.tail.prev
this.tail.next = null
    } 
else if (counter === index) {
     current.prev.next = current.next
     current.next.prev = current.prev
break
    }
    counter++
   }
  }
}

• reverse：翻转链表，实现如下代码：

reverse() {
  let current = this.head
  let prev = null
while (current) {
   let next = current.next
   current.next = prev
   current.prev = next
   prev = current
   current = next
  }
this.tail = this.head
this.head = prev
}

• swap：交换两个节点数据，实现如下代码：

swap(index1, index2) {
if (index1 > index2) {
return this.swap(index2, index1)
  }
  let current = this.head
  let counter = 0
let firstNode
while(current !== null) {
if (counter === index1 ){
        firstNode = current
    } 
else if (counter === index2) {
      let temp = current.data
      current.data = firstNode.data
      firstNode.data = temp
    }
    current = current.next
    counter++
  }
return true
}

• isEmpty：查询链表是否为空，实现如下代码：

isEmpty() {
return this.length() < 1
}

• length：查询链表长度，实现如下代码：

length() {
  let current = this.head
  let counter = 0
while(current !== null) {
    counter++
    current = current.next
  }
return counter
}

• traverse：遍历链表，实现如下代码：

traverse(fn) {
  let current = this.head
while(current !== null) {
    fn(current)
    current = current.next
  }
return true
}

如上代码，有了上面 length 方法的遍历实现，traverse 也就不难理解了，它接受一个遍历执行函数，在 while 循环中进行调用。

• find：查找某个节点的索引，实现如下代码：

find(item) {
  let current = this.head
  let counter = 0
while( current ) {
if( current.data == item ) {
return counter
    }
    current = current.next
    counter++
  }
return false
}

至此，我们就实现了所有双向链表（DoublyLinkedList）的方法。仔细分析整个实现过程，你可以发现：双向链表的实现并不复杂，在手写过程中，需要开发者做到心中有 “表”，考虑到当前节点的 next 和 prev 取值，逻辑上还是很简单的。

树

前端开发者应该对树这个数据结构丝毫不陌生，不同于之前介绍的所有数据结构，树是非线性的。因为树决定了其存储的数据直接有明确的层级关系，因此对于维护具有层级特性的数据，树是一个天然良好的选择。

事实上，树有很多种分类，但是它们都具有以下特性：

• 除了根节点以外，所有的节点都有一个父节点；
• 每一个节点都可以有若干子节点，如果没有子节点，则称此节点为叶子节点；
• 一个节点所拥有的叶子节点的个数，称之为该节点的度，因此叶子节点的度为 0；
• 所有节点中，最大的度为整棵树的度；
• 树的最大层次称为树的深度。

我们这里对二叉搜索树展开分析。二叉树算是最基本的树，因为它的结构最简单，每个节点至多包含两个子节点。二叉树又非常有用，因为根据二叉树，我们可以延伸出二叉搜索树（BST）、平衡二叉搜索树（AVL）、红黑树（R/B Tree）等。

二叉搜索树有以下特性：

• 左子树上所有结点的值均小于或等于它的根结点的值；
• 右子树上所有结点的值均大于或等于它的根结点的值；
• 左、右子树也分别为二叉搜索树。

根据其特性，我们实现二叉搜索树还是应该先构造一个节点类，如下代码：

class Node { 
  constructor(data) { 
this.left = null
this.right = null
this.value = data
  } 
}

然后我们实现二叉搜索树的以下方法。

• insertNode：根据一个父节点，插入一个子节点，如下代码：

insertNode(root, newNode) {
if (newNode.value < root.value) {
    (!root.left) ? root.left = newNode : this.insertNode(root.left, newNode)
  } else {
    (!root.right) ? root.right = newNode : this.insertNode(root.right, newNode)
  }
}

• insert：插入一个新节点，如下代码：

insert(value) {
    let newNode = new Node(value)
if (!this.root) {
this.root = newNode
    } else {
this.insertNode(this.root, newNode)
    }
}

理解这两个方法是理解二叉搜索树的关键，如果你理解了这两个方法，下面的其他方法也就 “不在话下”。

我们可以看到，insertNode 方法先判断目标父节点和插入节点的值，如果插入节点的值更小，则考虑放到父节点的左边，接着递归调用 this.insertNode(root.left, newNode)；如果插入节点的值更大，以此类推即可。insert 方法只是多了一步构造 Node 节点实例，接下来区分有无父节点的情况，调用 this.insertNode 方法即可。

• removeNode：根据一个父节点，移除一个子节点，如下代码：

removeNode(root, value) {
if (!root) {
return null
    }
if (value < root.value) {
      root.left = this.removeNode(root.left, value)
return root
    } else if (value > root.value) {
      root.right = tis.removeNode(root.right, value)
return root
    } else {
if (!root.left && !root.right) {
        root = null
return root
      }
if (root.left && !root.right) {
        root = root.left
return root
      } 
else if (root.right) {
        root = root.right
return root
      }
      let minRight = this.findMinNode(root.right)
      root.value = minRight.value
      root.right = this.removeNode(root.right, minRight.value)
return root
    }
  }

• remove：移除一个节点，如下代码：

remove(value) {
if (this.root) {
this.removeNode(this.root, value)
    }
}
findMinNode(root) {
if (!root.left) {
return root
    } else {
return this.findMinNode(root.left)
    }
}

上述代码不难理解，唯一需要说明的是：当需要删除的节点含有左右两个子节点时，因为我们要把当前节点删除，就需要找到合适的 “补位” 节点，这个 “补位” 节点一定在该目标节点的右侧树当中，因为这样才能保证 “补位” 节点的值一定大于该目标节点的左侧树所有节点，而该目标节点的左侧树不需要调整；同时为了保证 “补位” 节点的值一定要小于该目标节点的右侧树值，因此要找的 “补位” 节点其实就是该目标节点的右侧树当中最小的那个节点。

• searchNode：根据一个父节点，查找子节点，如下代码：

searchNode(root, value) {
if (!root) {
return null
    }
if (value < root.value) {
return this.searchNode(root.left, value)
    } else if (value > root.value) {
return this.searchNode(root.right, value)
    }
return root
}

• search：查找节点，如下代码：

search(value) {
if (!this.root) {
return false
    }
return Boolean(this.searchNode(this.root, value))
}

• preOrder：前序遍历，如下代码：

preOrder(root) {
if (root) {
      console.log(root.value)
this.preOrder(root.left)
this.preOrder(root.right)
    }
}

• InOrder：中序遍历，如下代码：

inOrder(root) {
if (root) {
this.inOrder(root.left)
      console.log(root.value)
this.inOrder(root.right)
    }
}

• PostOrder：后续遍历，如下代码：

postOrder(root) {
if (root) {
this.postOrder(root.left)
this.postOrder(root.right)
      console.log(root.value)
    }
}

上述前、中、后序遍历的区别其实就在于console.log(root.value) 方法执行的位置。

图

图是由具有边的节点集合组成的数据结构，图可以是定向的或不定向的。图也是应用最广泛的数据结构之一，真实场景中处处有图。当然更多概念还是需要你先进行了解，尤其是图的几种基本元素。

• 节点：Node
• 边：Edge
• |V|：图中顶点（节点）的总数
• |E|：图中的连接总数（边）

这里我们主要实现一个有向图，Graph 类，如下代码：

class Graph {
  constructor() {
this.AdjList = new Map()
  }
}

我们先通过创建节点，来创建一个图，如下代码：

let graph = new Graph();
graph.addVertex('A')
graph.addVertex('B')
graph.addVertex('C')
graph.addVertex('D')

• 添加顶点：addVertex，如下代码：

addVertex(vertex) {
if (!this.AdjList.has(vertex)) {
this.AdjList.set(vertex, [])
  } else {
throw 'vertex already exist!'
  }
}

这时候，A、B、C、D 顶点都对应一个数组，如下代码所示：

'A' => [],
'B' => [],
'C' => [],
'D' => []

数组将用来存储边。我们设计图预计得到如下关系：

Map {
'A' => ['B', 'C', 'D'],
'B' => [],
'C' => ['B'],
'D' => ['C']
}

根据以上描述，其实已经可以把图画出来了。addEdge 需要两个参数：一个是顶点，一个是连接对象 Node。我们看看添加边是如何实现的。

• 添加边：addEdge，如下代码：

 addEdge(vertex, node) {
    if (this.AdjList.has(vertex)) {
      if (this.AdjList.has(node)){
        let arr = this.AdjList.get(vertex)
        if (!arr.includes(node)){
          arr.push(node)
        }
      } else {
        throw `Can't add non-existing vertex ->'${node}'`
      }
    } else {
      throw `You should add '${vertex}' first`
    }
}

理清楚数据关系，我们就可以打印图了，其实就是一个很简单的 for…of 循环：

• 打印图：print，如下代码：

print() {
for (let [key, value] of this.AdjList) {
    console.log(key, value)
  }
}

剩下的内容就是遍历图了。遍历分为广度优先算法（BFS）和深度优先搜索算法（DFS）。我们先来看下广度优先算法（BFS）。

广度优先算法遍历，如下代码：

createVisitedObject() {
  let map = {}
for (let key of this.AdjList.keys()) {
    arr[key] = false
  }
return map
}
bfs (initialNode) {
  let visited = this.createVisitedObject()
  let queue = []
  visited[initialNode] = true
  queue.push(initialNode)
while (queue.length) {
    let current = queue.shift()
    console.log(current)
    let arr = this.AdjList.get(current)
for (let elem of arr) {
if (!visited[elem]) {
        visited[elem] = true
        queue.push(elem)
      }
    }
  }
}

如上代码所示，我们来进行简单总结。广度优先算法（BFS），是一种利用队列实现的搜索算法。对于图来说，就是从起点出发，对于每次出队列的点，都要遍历其四周的点。

因此 BFS 的实现步骤：

• 起始节点作为起始，并初始化一个空对象——visited；
• 初始化一个空数组，该数组将模拟一个队列；
• 将起始节点标记为已访问；
• 将起始节点放入队列中；
• 循环直到队列为空。

深度优先算法，如下代码：

createVisitedObject() {
  let map = {}
for (let key of this.AdjList.keys()) {
    arr[key] = false
  }
return map
}
 dfs(initialNode) {
    let visited = this.createVisitedObject()
this.dfsHelper(initialNode, visited)
  }
  dfsHelper(node, visited) {
    visited[node] = true
    console.log(node)
    let arr = this.AdjList.get(node)
for (let elem of arr) {
if (!visited[elem]) {
this.dfsHelper(elem, visited)
      }
    }
  }
}

如上代码，对于深度优先搜索算法（DFS），我把它总结为：“不撞南墙不回头”，从起点出发，先把一个方向的点都遍历完才会改变方向。换成程序语言就是：“DFS 是利用递归实现的搜索算法”。因此 DFS 的实现过程：

• 起始节点作为起始，创建访问对象；
• 调用辅助函数递归起始节点。

BFS 的实现重点在于队列，而 DFS 的重点在于递归，这是它们的本质区别。

总结

这一讲我们介绍了和前端最为贴合的几种数据结构，事实上数据结构更重要的是应用，我希望你能够做到：在需要的场景，能够想到最为适合的数据结构处理问题。请你务必掌握好这些内容，接下来的几讲都需要对数据结构有一个较为熟练的掌握和了解。我们马上进入数据结构的应用学习。

本讲内容总结如下：

随着需求的复杂度上升，前端工程师越来越离不开数据结构。是否能够掌握这个难点内容，将是进阶的重要考量。下一讲，我们将解析数据结构在前端中的具体应用场景，来帮助你加深理解，做到灵活应用。