数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
队列在日常生活中很常见,当我们排队买票看电影的时候,排在队列前面的人先入场,排在队列后面的人只能后入场。在计算机系统中常用先进先出(First In First Out)的队列来表示这种场景。
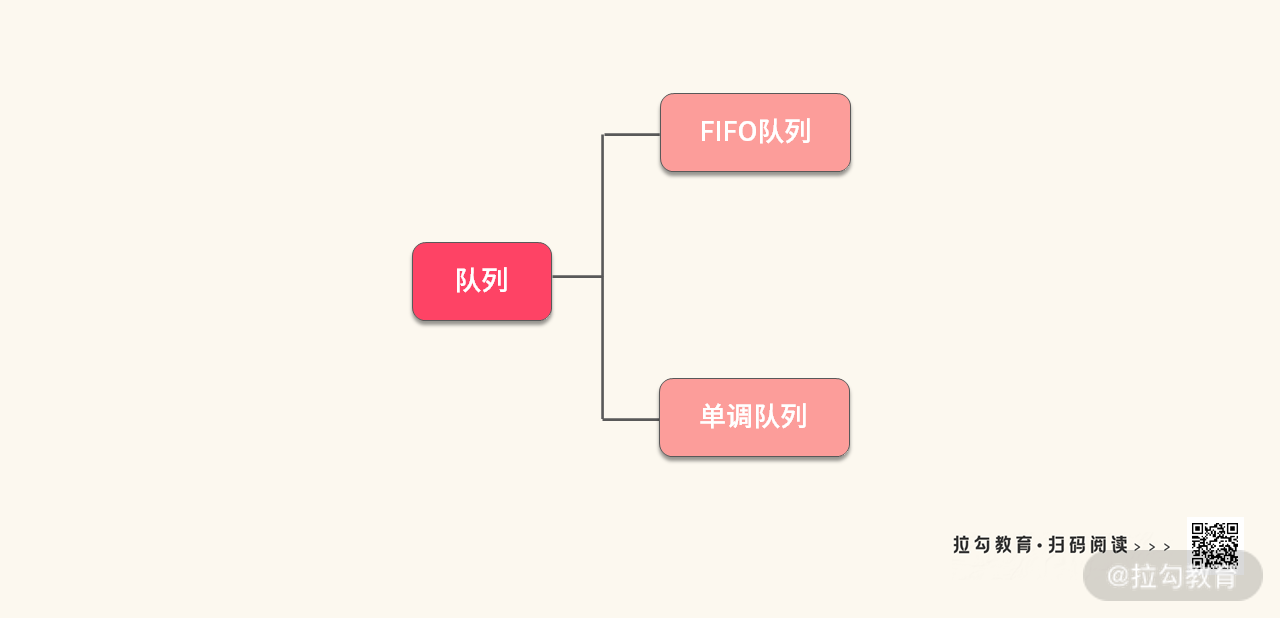
但是除了这种 FIFO 队列以外,还有一种队列需要注意,就是单调队列,由于课本上不常讲,面试中又容易出现,因此需要格外注意。让我们一起把这个数据结构的知识图谱丰富起来。
下面我要介绍的内容在实际的工程应用中也经常会用到,比如:
- Redis 的消息队列,用来搭建秒杀系统;
- LevelDB 的写入队列,可以保证数据写入的顺序;
- Qemu 的 Ring Buffer,用来完成数据的高效传输。
它们是很多基础设施的基本算法,比如操作系统、数据库、TCP/IP 协议栈等。OK, Let’s Go!
FIFO 队列
我们先从基本的 FIFO 队列入手,其特点用动画表示如下:
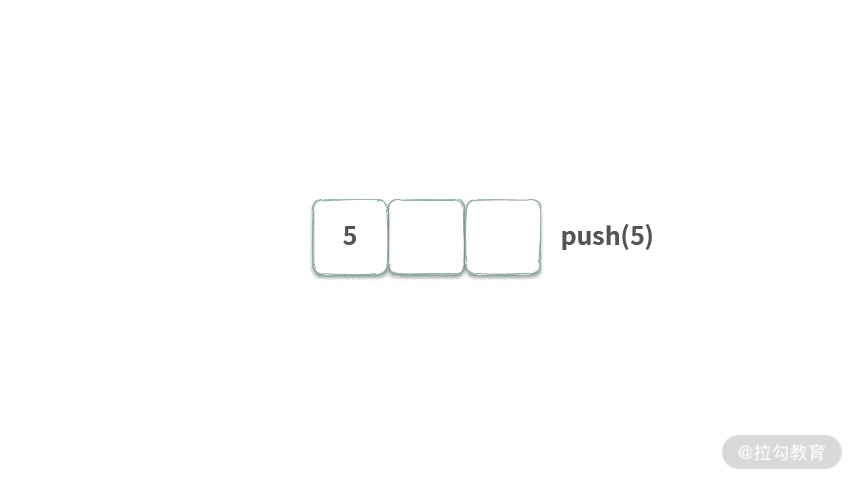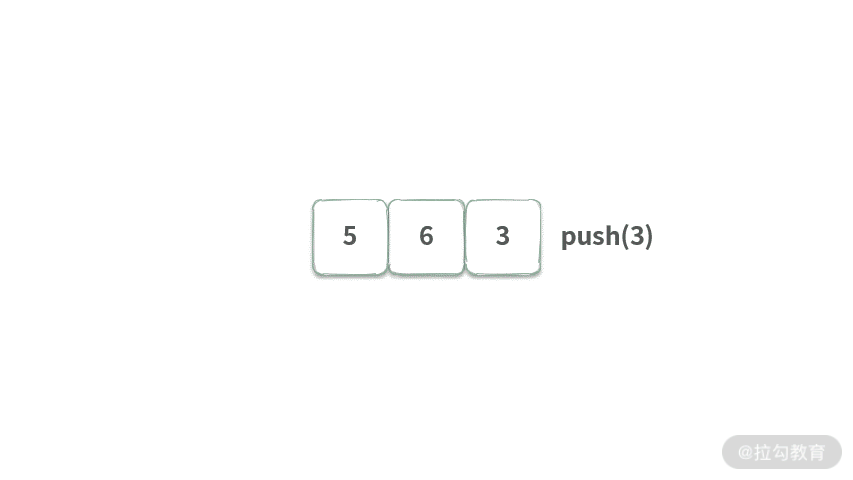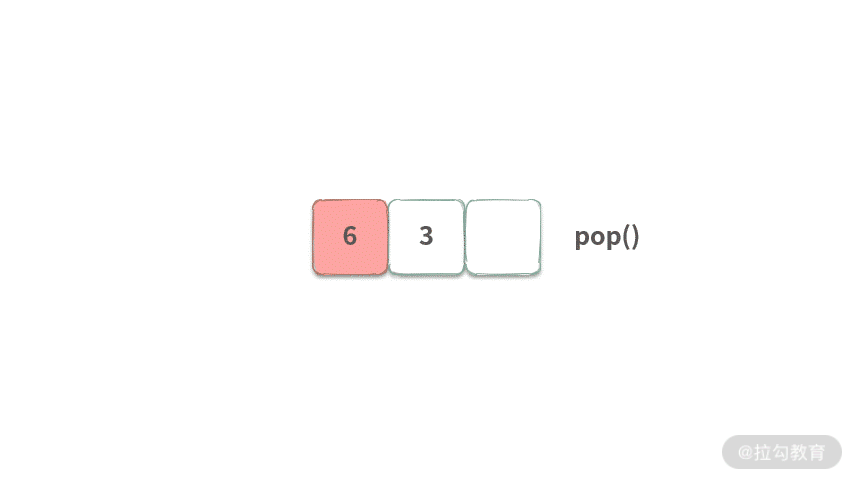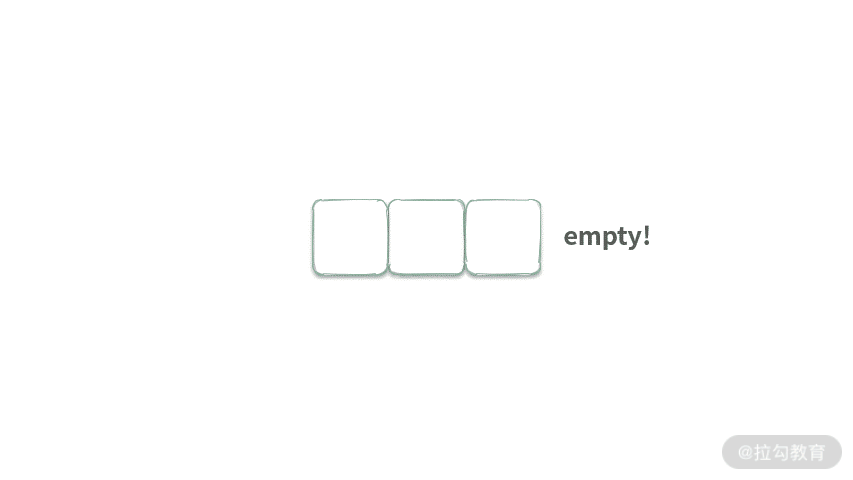
可以发现 FIFO 有两个特点:
- push 元素时,总是将元素放在队列尾部;
- pop 元素时,总是将队列首部的元素扔掉。
但只知道 FIFO 的特性,并不能从容地应对复杂的面试。因此我们还需要进一步对 FIFO 加以深挖,力求在面试中游刃有余。接下来我将通过大厂面试题,带你学习这块重点知识。
例 1:二叉树的层次遍历(两种方法)
【题目】从上到下按层打印二叉树,同一层结点按从左到右的顺序打印,每一层打印到一行。
输入:
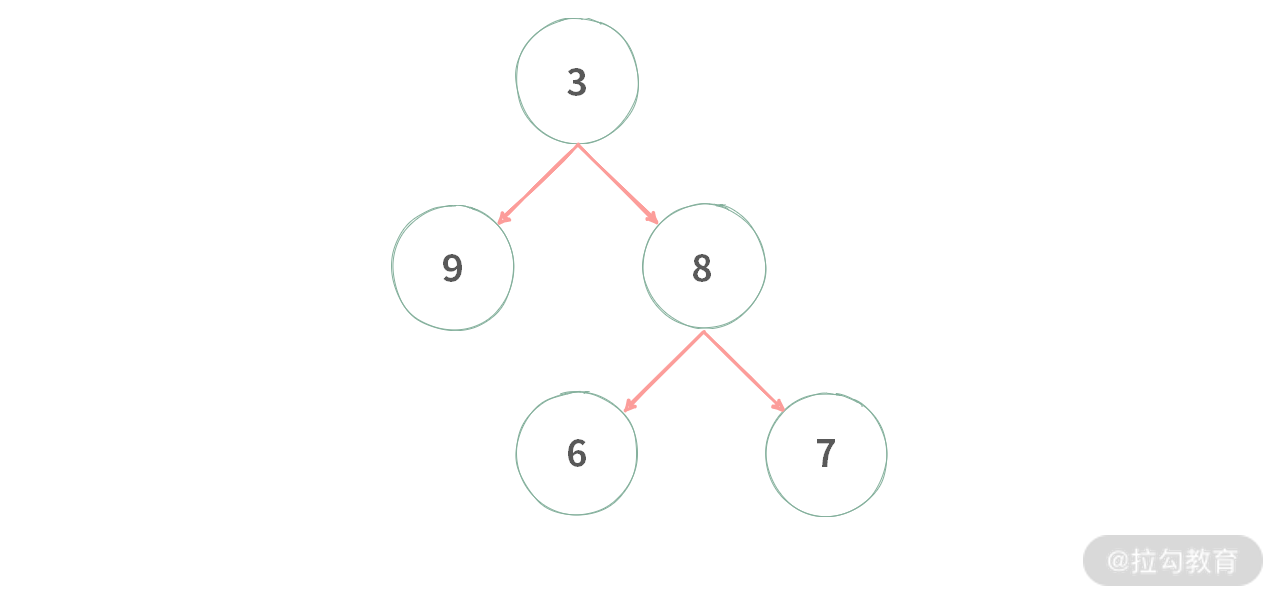
输出:[[3], [9, 8], [6, 7]]
public class TreeNode {int val = 0;TreeNode left = null;TreeNode right = null;}
【分析】这道题已经在非常多的大厂面试中出现过了,比如微软,美团,腾讯等,因此你务必要掌握题目涉及的思想和原理。在真正开始写代码之前,我们还是参考 “第 01 讲”中给出的深度思考的路线,从分析题目到写出代码 “走” 一遍。
1. 模拟
首先我们在这棵树上进行模拟,动图演示效果如下所示:
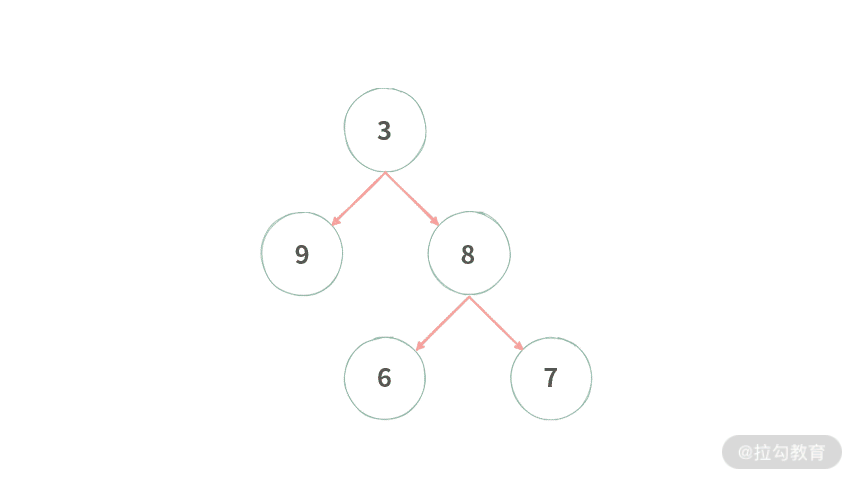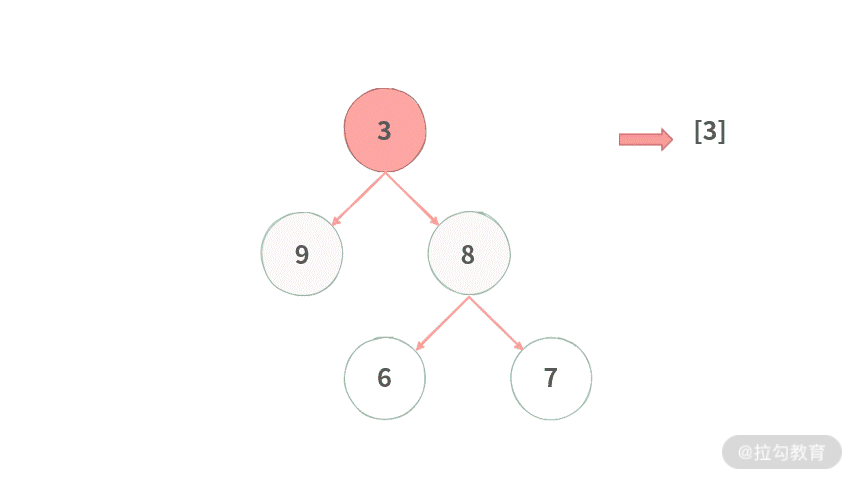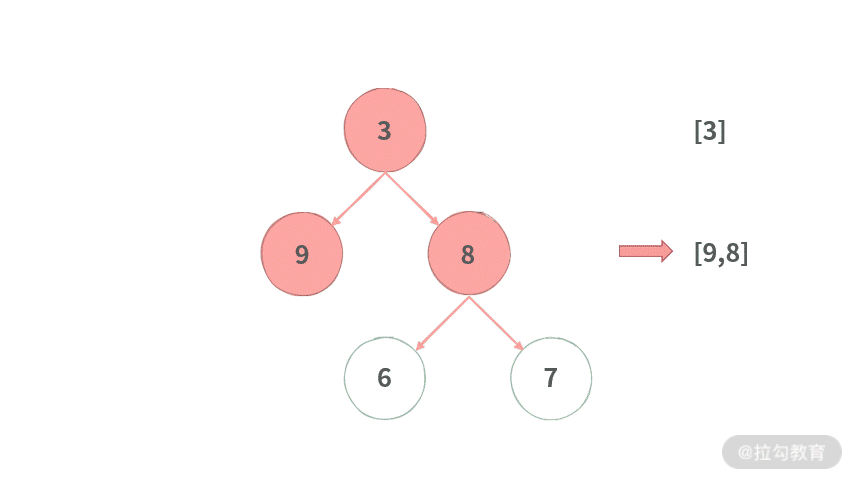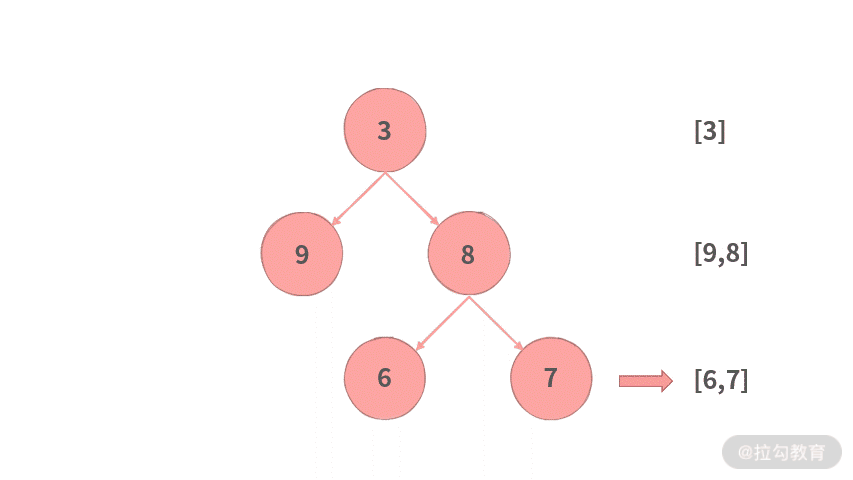
2. 规律
通过运行的模拟,可以总结出以下两个特点。
(1)广度遍历(层次遍历):由于二叉树的特点,当我们拿到第 N 层的结点 A 之后,可以通过 A 的 left 和 right 指针拿到下一层的结点。
(2)顺序输出:每层输出时,排在左边的结点,它的子结点同样排在下一层最左边。
3. 匹配
当你发现题目具备广度遍历(分层遍历)和顺序输出的特点,就应该想到用FIFO 队列来试一试。
4.. 边界
关于二叉树的边界,需要考虑一种空二叉树的情况。当遇到一棵空的二叉树,有两种解决办法。
(1)特殊判断:如果发现是一棵空二叉树,就直接返回空结果。
(2)制定一个规则:不要让空指针进入到 FIFO 队列。
我个人比较喜欢第 2 种方案,因为代码一致性更好(一致性是指不需要为各种特殊情况再添加额外的 if/else 来处理)。所以接下来我将从 “制定一个规则:不要让空指针进入队列” 上考虑代码的实现。
【画图】当我们拿到一道题,脑海中已经关联了相应的数据结构:FIFO 队列,下面就可以利用它来画图了。
不过,二叉树的层次遍历与标准的 FIFO 队列不太一样,需要在每一层开始处理之前,记录一下 Queue Size(当前层里面结点的个数),演示如下图所示:
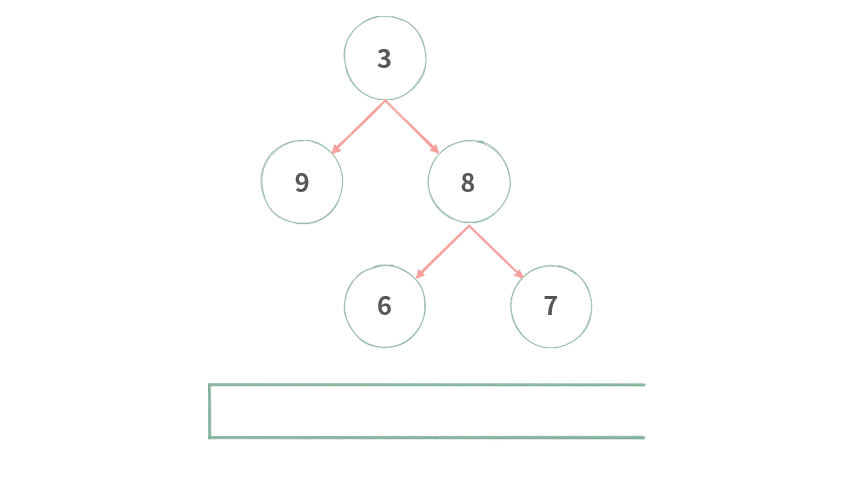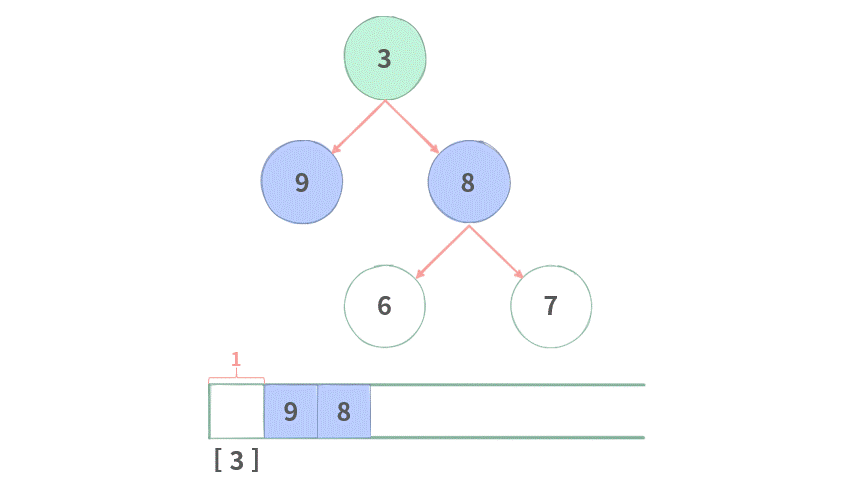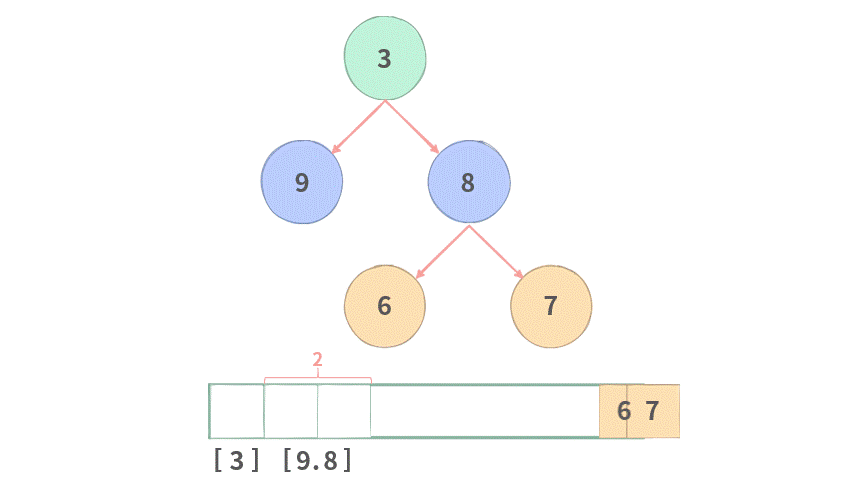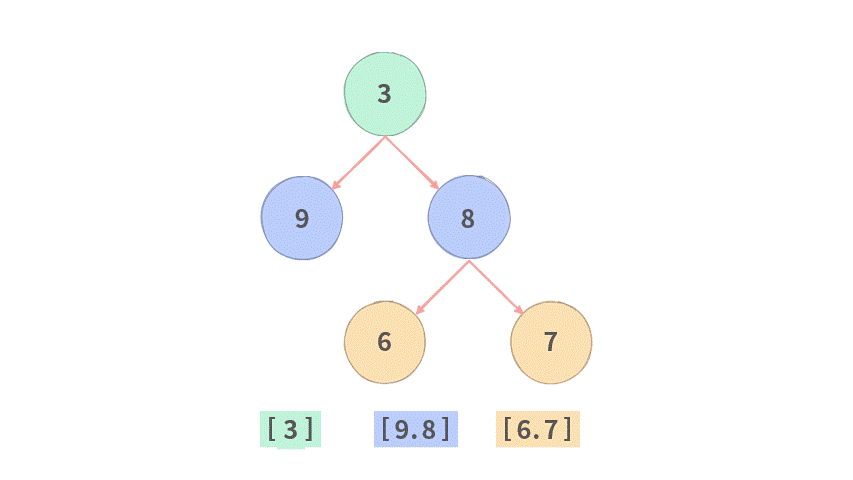
Step1. 在一开始首先将根结点 3 加入队列中。
Step 2. 开始新一层遍历,记录下当前队列长度 QSize=1,初始化当前层存放结果的[]。
Step 3. 将结点 3 出队,然后将其放到当前层中。
Step 4. 再将结点 3 的左右子结点分别入队。QSize = 1 的这一层已经处理完毕。
Step 5. 开始新一层的遍历。记录下新一层的 QSize = 2,初始化新的当前层存放当前层结果的[]。
Step 6. 从队列中取出 9,放到当前层结果中。结点 9 没有左右子结点,不需要继续处理左右子结点。
Step 7. 从队列中取出 8,放到当前层结果中。
Step 8. 将结点 8 的左右子结点分别入队。此时,QSize = 2 的部分已经全部处理完成。
Step 9.开始新一层的遍历,记录下当前队列中的结点数 QSize = 2,并且生成存放当前层结果的 list[]。
Step 10. 将队首结点 6 出队放到当前层结果中。结点 6 没有左右子结点,没有元素要入队。
Step 11. 将队首结点 7 出队,放到当前层结果中。结点 7 没有左右子结点,没有元素要入队。
结束,返回我们层次遍历的结果。
【代码】现在我们有解题思路,也有运行图,接下来就可以写出以下核心代码(解析在注释里):
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {Queue<TreeNode> Q = new LinkedList<>();if (root != null) {Q.offer(root);}List<List<Integer>> ans = new LinkedList<>();while (Q.size() > 0) {final int qSize = Q.size();List<Integer> tmp = new LinkedList<>();for (int i = 0; i < qSize; i++) {TreeNode cur = Q.poll();tmp.add(cur.val);if (cur.left != null) {Q.offer(cur.left);}if (cur.right != null) {Q.offer(cur.right);}}ans.add(tmp);}return ans;}}
复杂度分析:由于二叉树的每个结点,我们都只访问了一遍,所以时间复杂度为 O(n)。如果不算返回的数组,那么空间复杂度为 O(k),这里的 k 表示二叉树横向最宽的那一层的结点数目。
【小结】写完代码之后,对 FIFO 队列进行一轮总结。现在除了知道先进先出的特点之外,还可以进一步细化知识点,如下图所示:
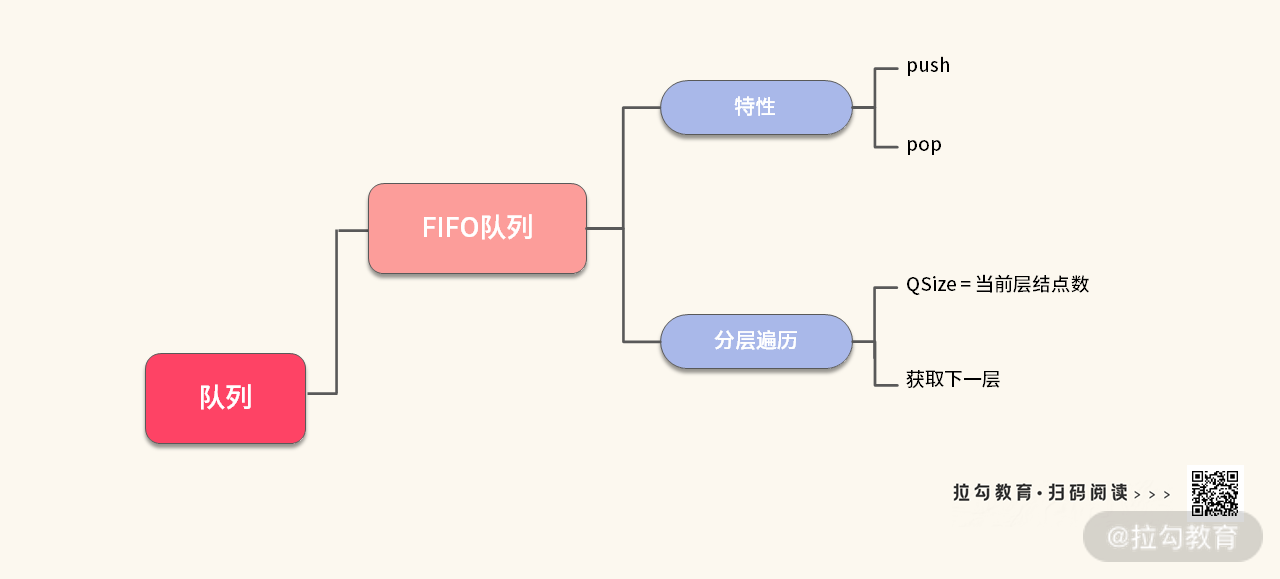
这道题是很多高频面试题的 “母题”,可以衍生出很多子题出来,因此建议你把这道题研究透彻。如果还有哪里不理解,可以在留言区提问。
在依靠 FIFO 队列的解法中,我们利用 QSize 得到当前层的元素个数,然后再开始执行 FIFO 是处理分层遍历的关键。下面我再向你介绍另外一种更直观的思路。
【解法二】再来回顾一下题目的特点:
- 分层遍历
- 顺序遍历
那么我们是不是可以用 List 来表示每一层,把下一层的结点统一放到一个新生成的 List 里面。示意图如下:
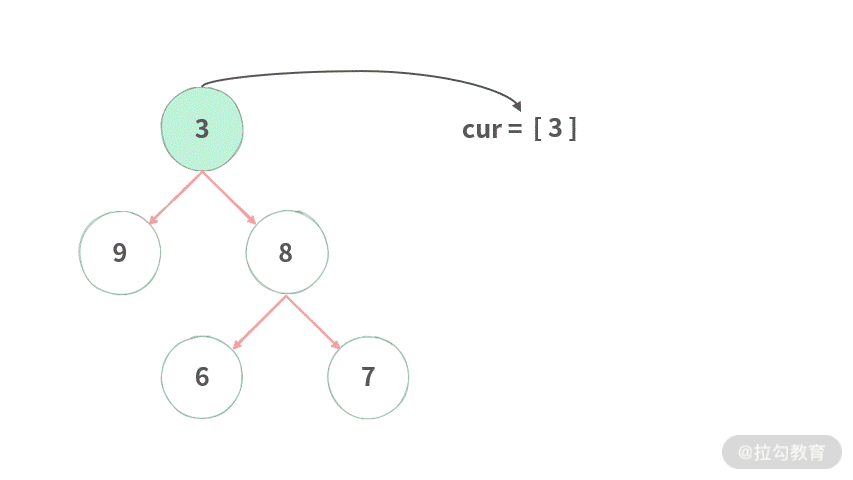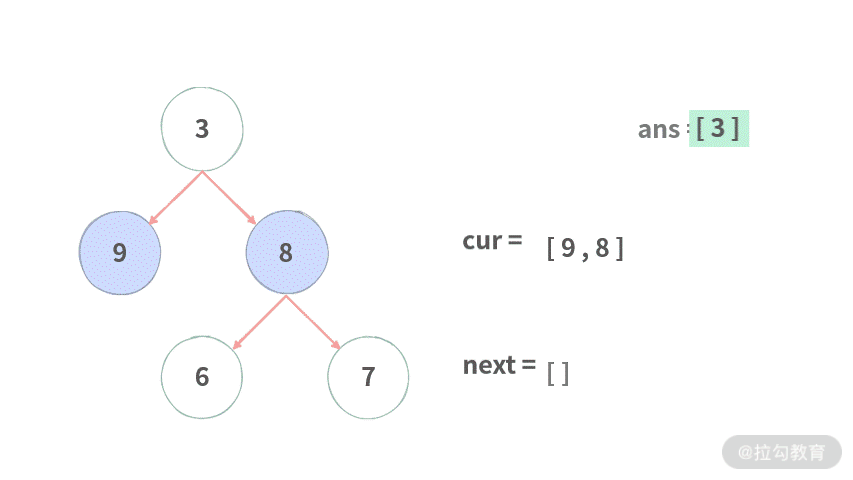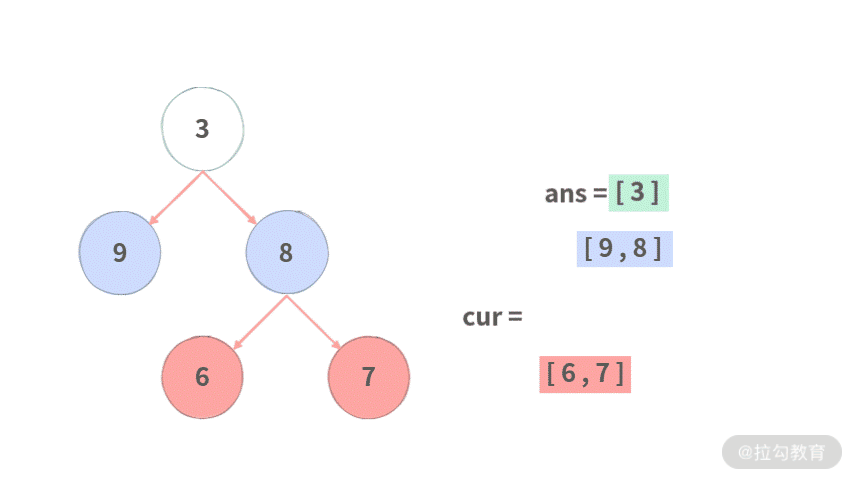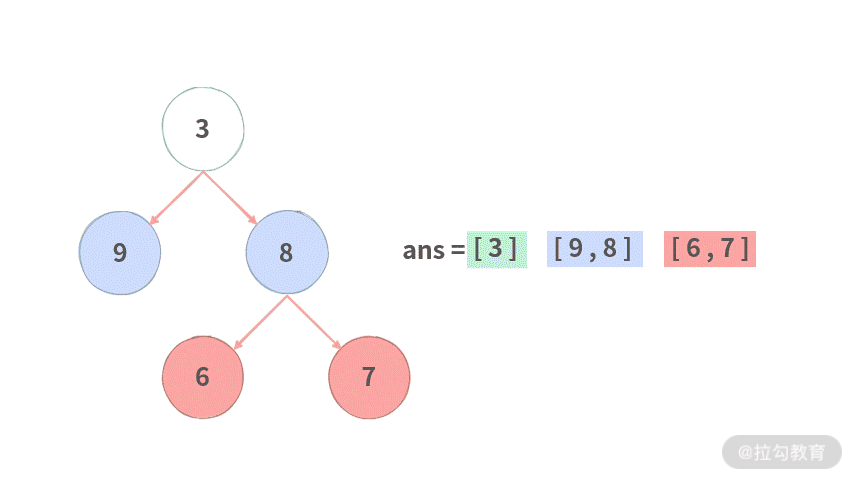
Step 1. 首先将结点 3 加入 cur,,形成 cur=[3]。
Step 2. 开始依次遍历当前层 cur, 这里 cur 只有结点 3,依次把结点 3 的左子结点和右子结点加入 next,形成 [9, 8]。
Step 3. 将 cur 指向 next,并且 next 设置为 []
Step 4. 依次遍历 cur,并将每个结点的左右子结点放到 next 中。
Step 5. 将 cur 指向 next。并依次遍历。由于这是最后一层,所以不会再生成 next。
Step 6. 最后得到层次遍历的结果。
根据这个思路,写出的代码如下(解析在注释里):
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ans = new ArrayList<>();List<TreeNode> curLevel = new ArrayList<>();if (root != null) {curLevel.add(root);}while (curLevel.size() > 0) {List<TreeNode> nextLevel = new ArrayList<>();List<Integer> curResult = new ArrayList<>();for (TreeNode cur: curLevel) {curResult.add(cur.val);if (cur.left != null) {nextLevel.add(cur.left);}if (cur.right != null) {nextLevel.add(cur.right);}}curLevel = nextLevel;ans.add(curResult);}return ans;}}
通过这个有趣的解法,我们知道,FIFO 队列不仅可以用 Queue 表示,还可以用两层 ArrayList 来表示,均可达到同样的效果。再把思路扩展一下,思考是否还有其他的形式可以表达 FIFO 队列呢?请看下面这道思考题。
【思考题】给定一棵二叉树,如下图所示,树中的结点稍微有点变化,定义如下:
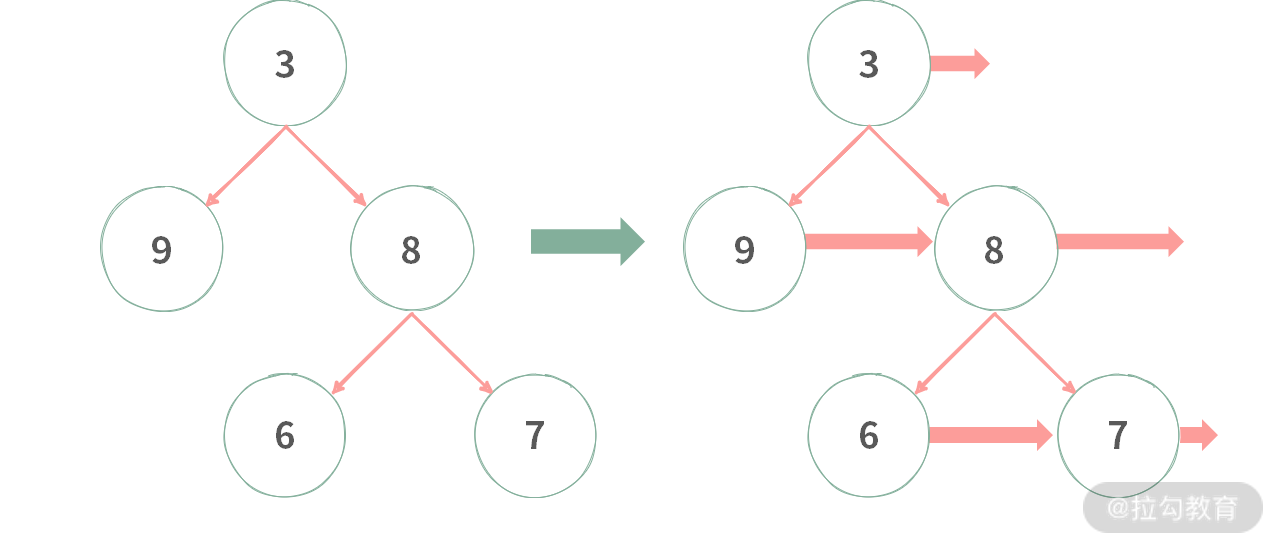
struct Node {int val = 0;Node *left = null;Node *right = null;Node *next = null;}
希望你能修改二叉树里所有的 next 指针,使其指向右边的结点,如果右边没有结点,那么设置为空指针。
至此,经过我们的 “浇灌”,FIFO 队列长出了更多的 “树叶”。为了方便你理解,我把解决这类题目的重点总结在一张大图中:
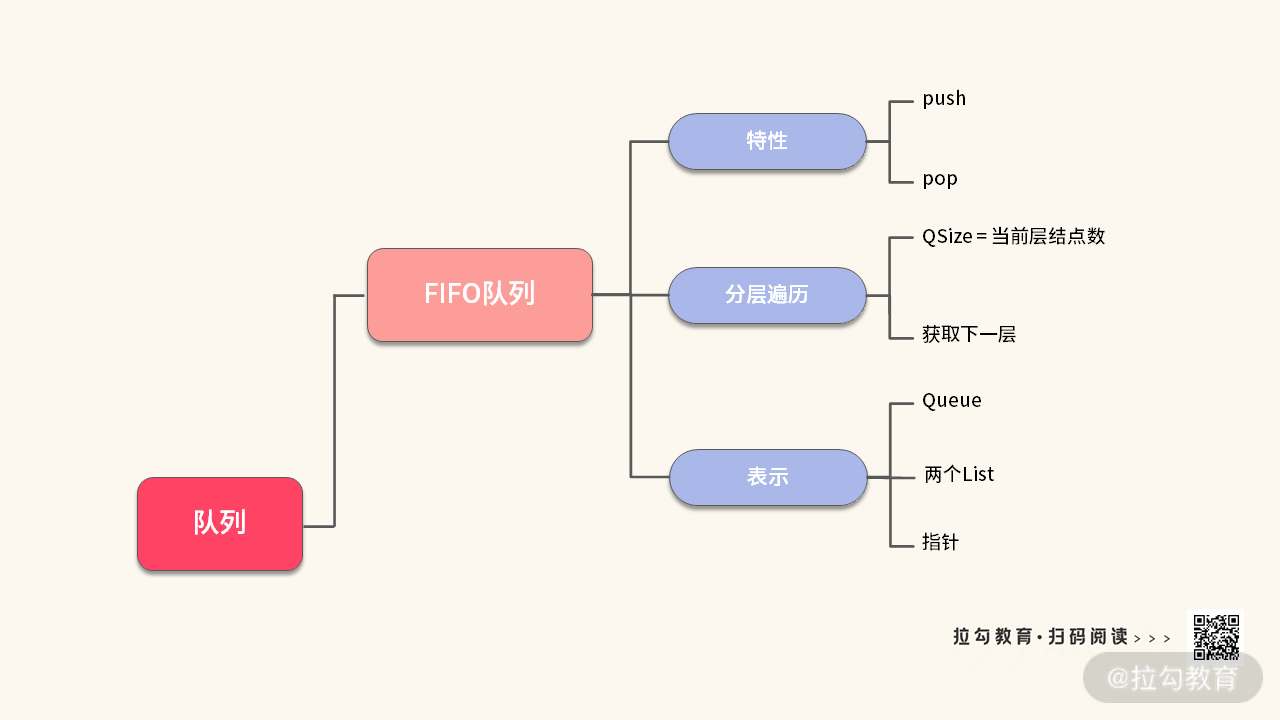
【题目扩展】切忌盲目刷题,其实只要吃透一道题,就可以解决很多类似的题目。只要掌握分层遍历的技巧,以后再碰到类似的题目,就再也难不住你了。这里我为你总结了一张关于 “二叉树的层次遍历” 的解题技巧,如下图所示:
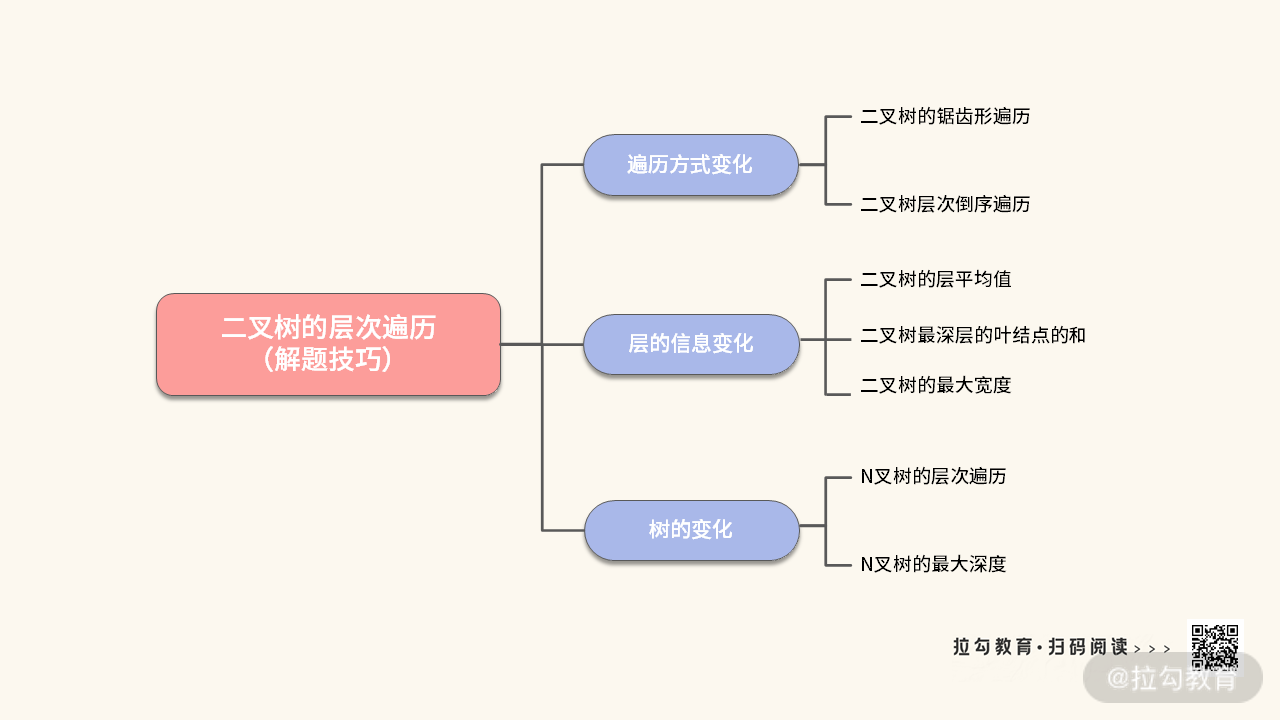
可以点开这里,查看题目的信息,代码。
例 2:循环队列
【题目】设计一个可以容纳 k 个元素的循环队列。需要实现以下接口:
class MyCircularQueue {public MyCircularQueue(int k);public boolean enQueue(int value);public boolean deQueue();public int Front();public int Rear();public boolean isEmpty();public boolean isFull();}
【分析】循环队列是一个书本上非常经典的关于队列的例子,在工程实践中也有很多运用,比如 Ring Buffer、生产者消费者队列。我去微软面试的时候也遇到了这道经典的题目。正好借着讲 FIFO 队列的机会,我再给你介绍一下循环队列。
循环队列的重点在于循环使用固定空间,难点在于控制好 front/rear 两个首尾指示器。这里我会介绍两种实现。
【方法 1】只使用 k 个元素的空间,三个变量 front, rear, used 来控制循环队列的使用。分别标记 k = 6 时,循环队列的三种情况,如下图所示:
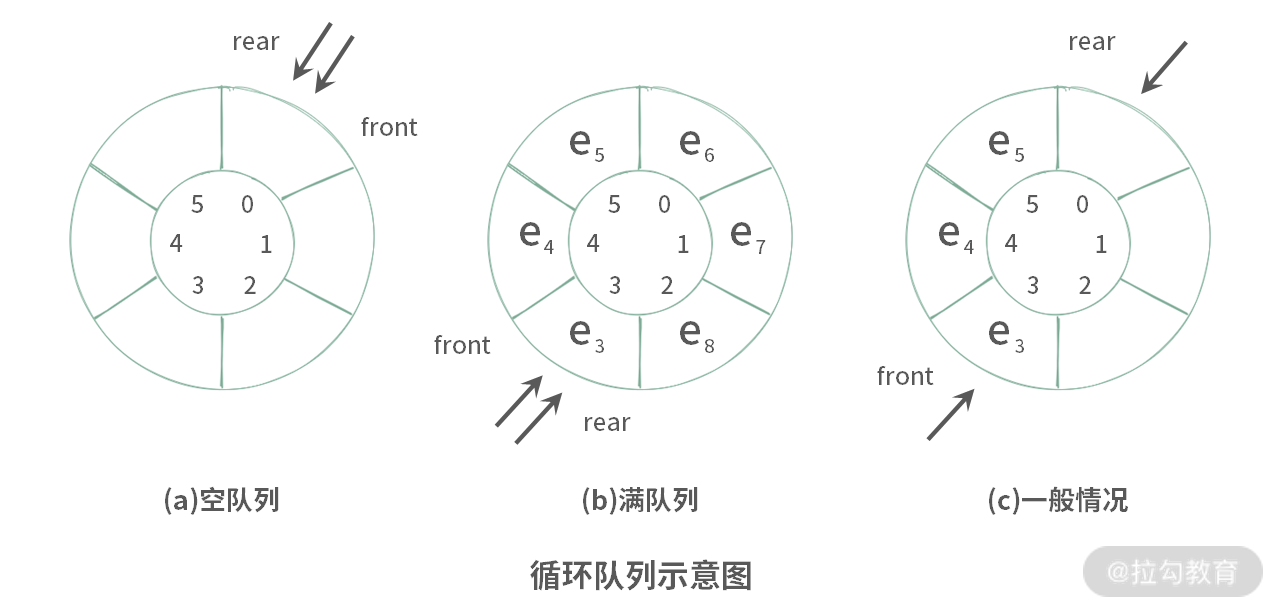
由图可知,在一般情况下,front 和 rear 都是不相等的。但是,如果仔细观察,你会发现在空队列与满队列的时候,front 和 rear 是相等的。那此时该怎么处理呢?
通过上述分析,可以知道只用 front 和 rear 两个变量,还不足以区分是空队列还是满队列,因此我们还需要用到额外的变量做进一步区分。一种比较简单的办法就是采用 used 变量,标记已经放了多少个元素在循环队列里面。
- 如图(a)所示,当队列为空的时候,used == 0;
- 如图(b)所示,当队列满的时候,used == k。
虽然从图片来看这是一个循环数组,但是面试官要求只能使用一个普通的数组来实现。在下标的移动上,要特别注意不要越界。下标只能在 [0, k-1] 范围里面移动。以下 3 点需要你格外注意,正常情况下:
- index = i 的后一个是 i + 1,前一个是 i - 1
- index = k-1 的后一个就是 index = 0
- index = 0 的前一个是 index = k-1
实际上,这三个式子都可以利用取模的技巧来统一处理:
- index = i 的后一个 (i + 1) % capacity
- index = i 的前一个 (i - 1 + capacity) % capacity
注意:所有的循环数组下标的处理都需要按照这个取模方法来。
通过前面的分析, 我们可以利用 front, rear, used 来写出循环队列的代码,如下所示(解析在注释里):
class MyCircularQueue {private int used = 0;private int front = 0;private int rear = 0;private int capacity = 0;private int[] a = null;public MyCircularQueue(int k) {capacity = k;a = new int[capacity];}public boolean enQueue(int value) {if (isFull()) {return false;}a[rear] = value;rear = (rear + 1) % capacity;used++;return true;}public boolean deQueue() {if (isEmpty()) {return false;}int ret = a[front];front = (front + 1) % capacity;used--;return true;}public int Front() {if (isEmpty()) {return -1;}return a[front];}public int Rear() {if (isEmpty()) {return -1;}int tail = (rear - 1 + capacity) % capacity;return a[tail];}public boolean isEmpty() {return used == 0;}public boolean isFull() {return used == capacity;}}
复杂度分析:入队操作与出队操作都是 O(1)。
【方法 2】方法 1 利用 used 变量对满队列和空队列进行了区分。实际上,这种区分方式还有另外一种办法,使用 k+1 个元素的空间,两个变量 front, rear 来控制循环队列的使用。具体如下:
- 在申请数组空间的时候,申请 k + 1 个空间;
- 在放满循环队列的时候,必须要保证 rear 与 front 之间有空隙。
如下图(此时 k = 5)所示:
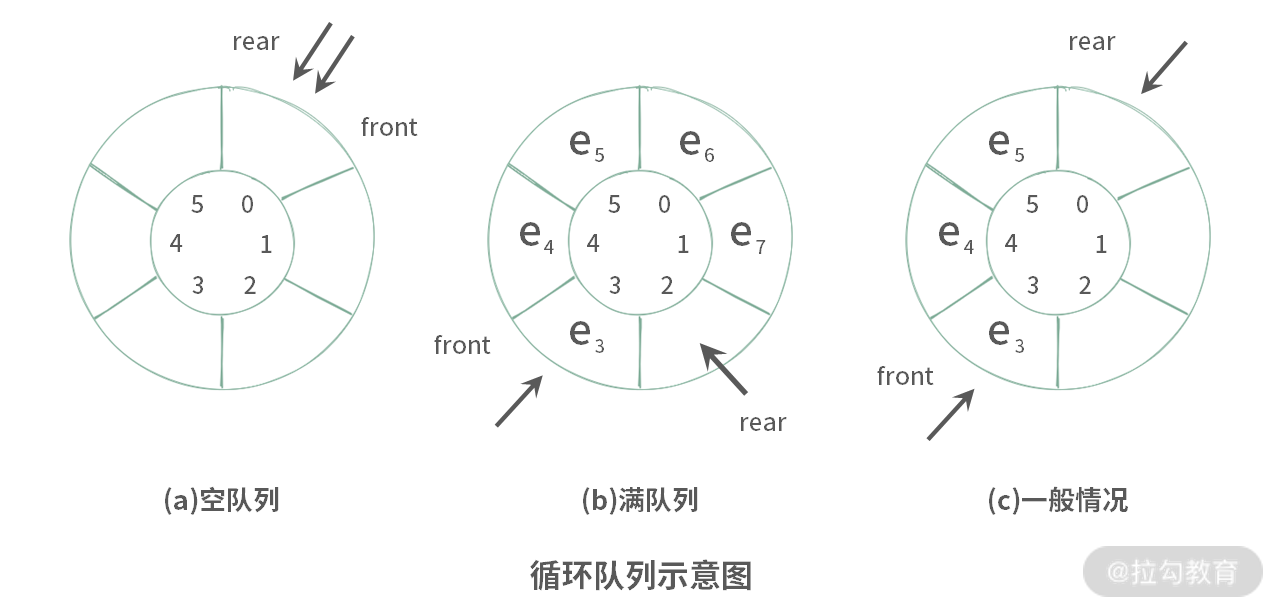
此时,可以发现,循环队列实际上是浪费了一个元素的空间。这个浪费的元素必须卡在 front 与 rear 之间。判断队列空或者满可以:
- front == rear 此时队列为空;
- (rear + 1) % capacity == front,此时队列为满。
注意:由于浪费了一个元素的空间,在申请数组的时候,要申请的空间大小为 k + 1, 并且 capacity 也必须为 k + 1。
除此之后,由于是循环数组,下标的活动范围是[0, k](capacity 为 k+1,所以最大只能取到 k)。下标的移动仍然需要利用取模的技巧。
【代码】第二种方法的思路,我们写出代码如下(解析在注释里):
class MyCircularQueue {private int front = 0;private int rear = 0;private int[] a = null;private int capacity = 0;public MyCircularQueue(int k) {capacity = k + 1;a = new int[k + 1];}public boolean enQueue(int value) {if (isFull()) {return false;}a[rear] = value;rear = (rear + 1) % capacity;return true;}public boolean deQueue() {if (isEmpty()) {return false;}front = (front + 1) % capacity;return true;}public int Front() {return isEmpty() ? -1 : a[front];}public int Rear() {int tail = (rear - 1 + capacity) % capacity;return isEmpty() ? -1 : a[tail];}public boolean isEmpty() {return front == rear;}public boolean isFull() {return (rear + 1) % capacity == front;}}
复杂度分析:入队与出队操作都是 O(1)。
我们介绍了两种方法来实现循环队列,下面我分别从相似点、差别,以及适用范围对这两种方法进行总结。
1. 相似点
两种方法都是利用了取模的技巧,强调一下,在取模的时候,如果需要向前移动,不要写成 (i - 1) % capacity,注意一定要加上 capacity 之后再取模,否则在 i = 0 的时候就出错了。
pre = (i - 1 + capacity) % capacity
2. 差别
这两种方法的唯一区别在于区分空队列与满队列时,方法不一样:
- 方法 1 引入了另外一个变量 used 进行区分
- 方法 2 采用了浪费一个存储空间的办法进行区分
3. 适用范围
你可能认为方法 2 在队列元素较大时,存在浪费的情况,实际上这两种办法都有不同的适用范围。
方法 1 的缺点在于控制变量较多,达到 3 个。而方法 2 虽然浪费了一个存储空间,但是控制变量较少,只有 2 个。
在多线程编程里面,控制变量越少,越容易实现无锁编程,因此,在无锁队列里面,利用方法 2 较容易实现无锁队列。
至此,我们已经可以将循环队列总结在一张思维导图中,如下图所示:
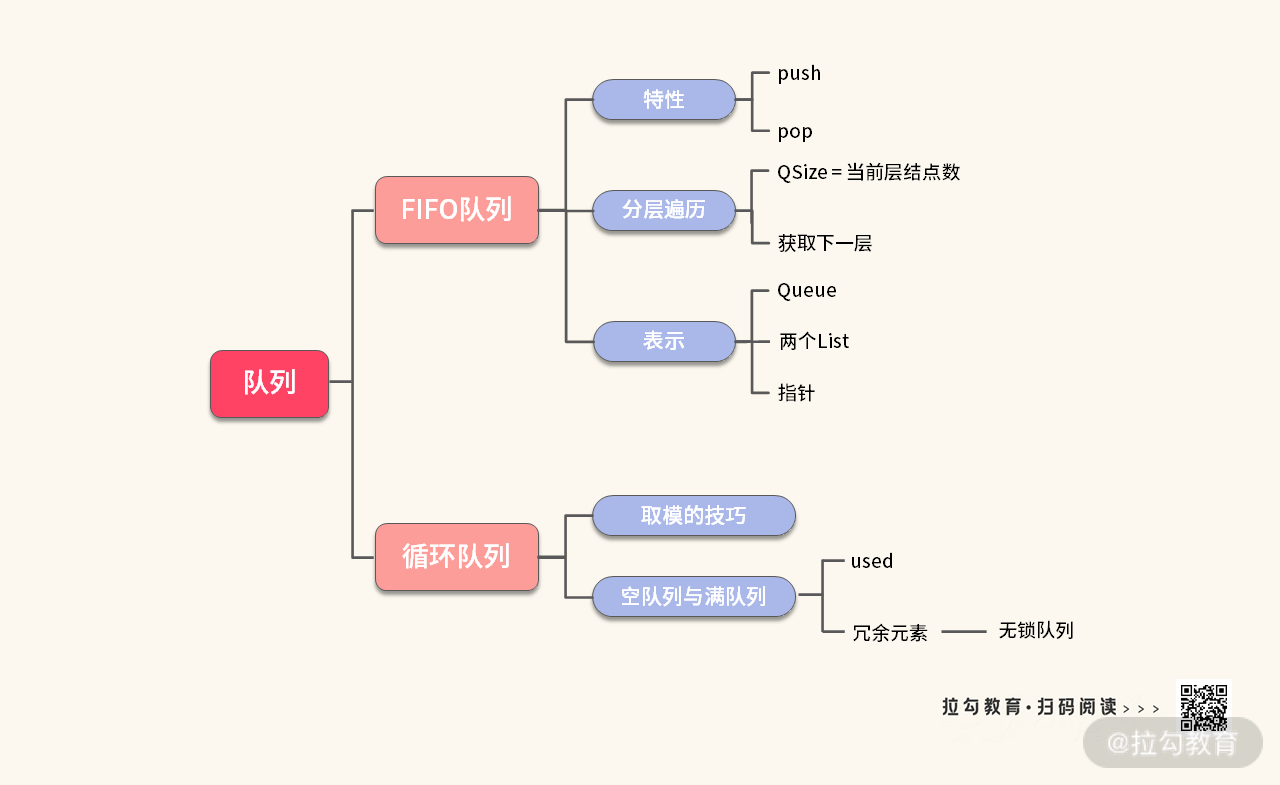
一会儿我们还会遇到循环队列的内容,比如用途等,下面我们先来讲讲单调队列。
单调队列
单调队列属于双端队列的一种。双端队列与 FIFO 队列的区别在于:
- FIFO 队列只能从尾部添加元素,首部弹出元素;
- 双端队列可以从首尾两端 push/pop 元素。
为了让你更直观地看出两者的区别,我分别绘制了 FIFO 队列和双端队列的图片,如下图所示:

FIFO 队列
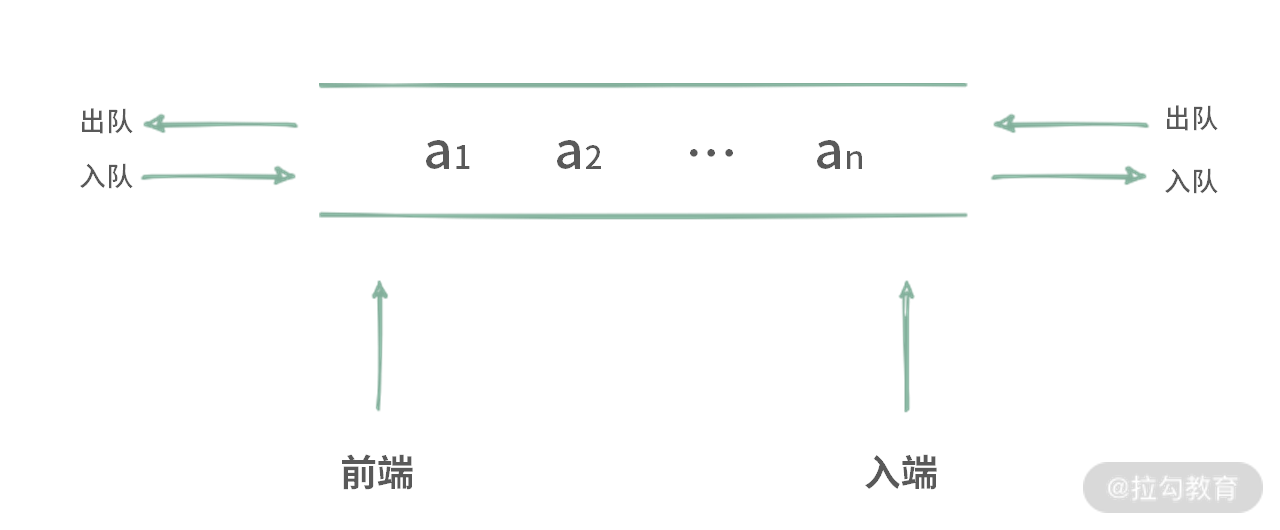
双端队列
虽然双端队列经常用于工程实践中,但在面试中出现得较多的往往是单调队列,因此,本讲我会重点介绍单调队列。
什么是单调队列
首先来看一下单调队列的定义:要求队列中的元素必须满足单调性,比如单调递增,或者单调整递减。那么在入栈与出栈的时候,就与普通的队列不一样了。
接下来我将以单调递减为例,详细讲解单调队列的特性,希望你可以自己推导单调递增的情况。如果有什么疑问可以在评论区留言,我会定期给大家解答。
单调队列在入队的时候,需要满足 2 点:
- 入队前队列已经满足单调性;
- 入队后队列仍然满足单调性。
这里以单调递减队列为例,具体操作如下图所示(为了更直观地展示,我将不同大小的数值绘制为不同的高度):
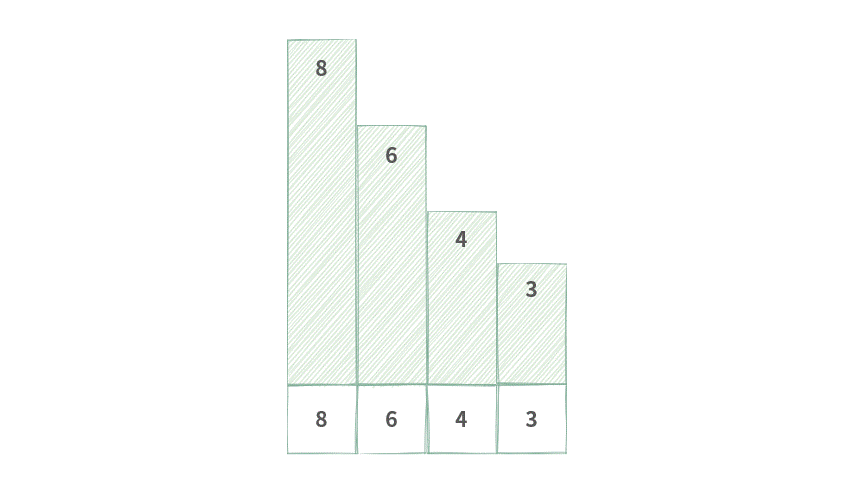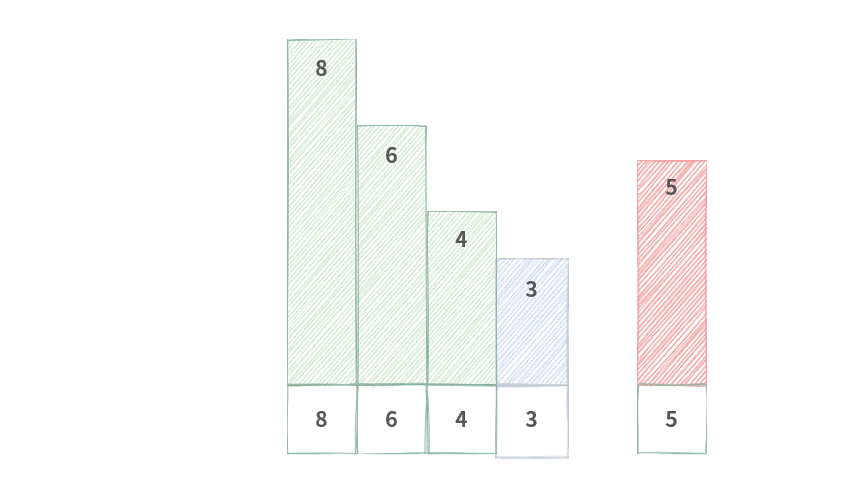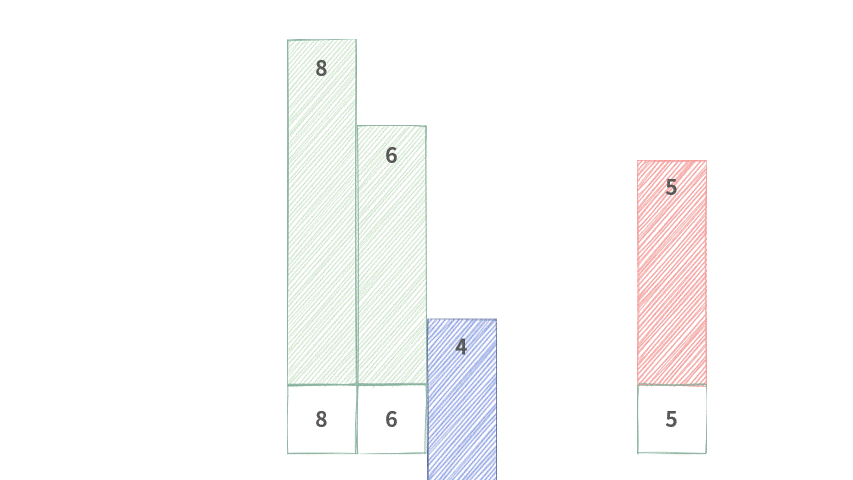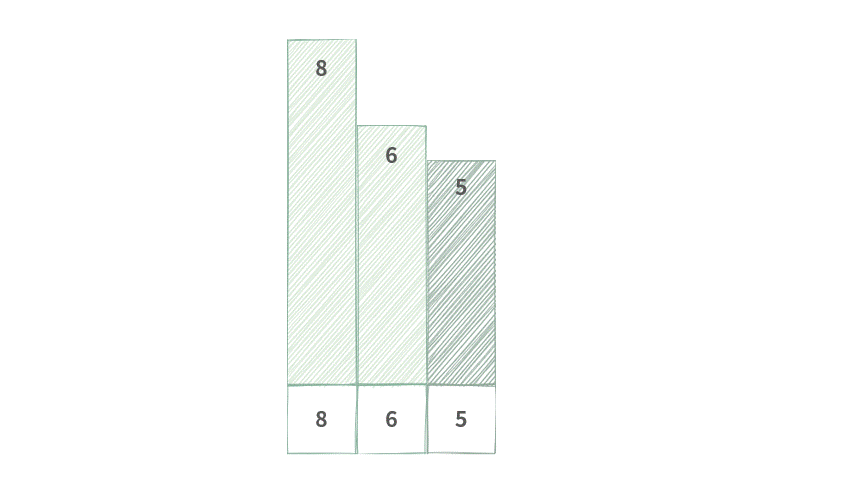
Step 1. 已有单调队列满足单调递减。
Step 2. 元素 5 要从尾部加入队列中。
Step 3. 元素 5 与尾部元素 3 比较,3 < 5,因此扔掉 3。
Step 4. 元素 5 与尾部元素 4 比较,4 < 5,因此扔掉 4。
Step 5. 元素 5 与尾部元素 6 比较,6 > 5,因此将 5 入队。
可以发现,每次入队的时候,为了保证队列的单调性,还要剔除掉尾部的元素。直到尾部的元素大于等于入队元素(因为是单调递减队列)。
private void push(int val) {while (!Q.isEmpty() && Q.getLast() < val) {Q.removeLast();}Q.addLast(val);}
单调队列在出队时,也与普通的队列出队方式不一样。出队时,需要给出一个 value,如果 value 与队首相等,才能将这个数出队,代码如下所示:
private void pop(int val) {if (!Q.isEmpty() && Q.getFirst() == val) {Q.removeFirst();}}
那么,采用这种比较特殊的入队与出队的方式有什么巧妙的地方呢?
- 入队之后,队首元素 Q.getFirst() 就是队列中的最大值。这个比较容易想到,因为我们这里是以单调递减队列为例,所以队首元素就是最大值。
- 出队时,如果一个元素已经被其他元素剔除出去了,就不会再出队。但如果一个元素是当前队列中的最大值,那么就会再出队。
关于这一点,你可以参考下面的动图演示(为了更清晰地演示此过程,被叉掉的元素还保留在原处,但实际上已经不在队列中了):
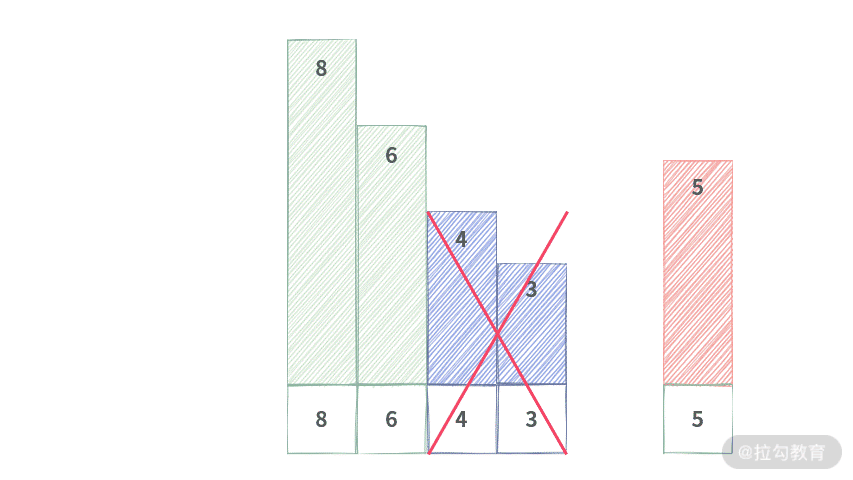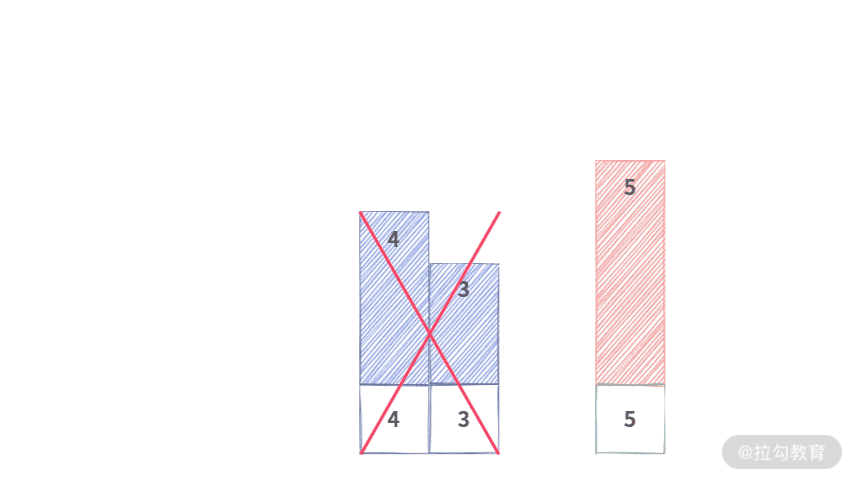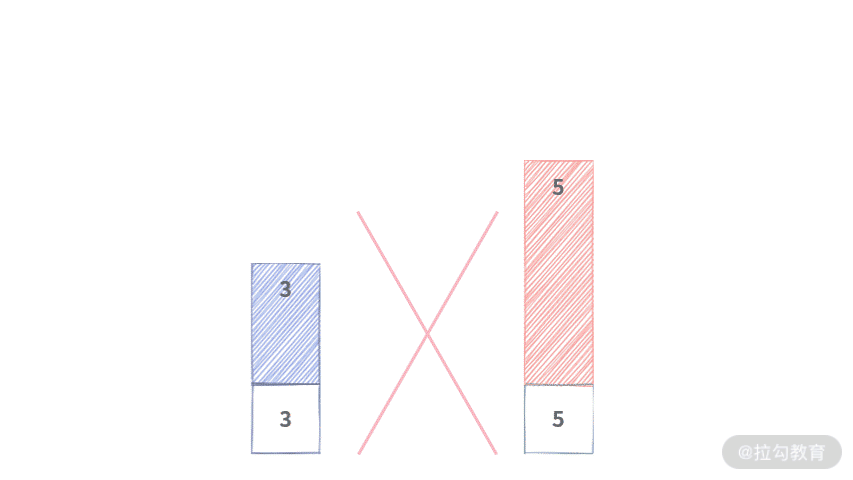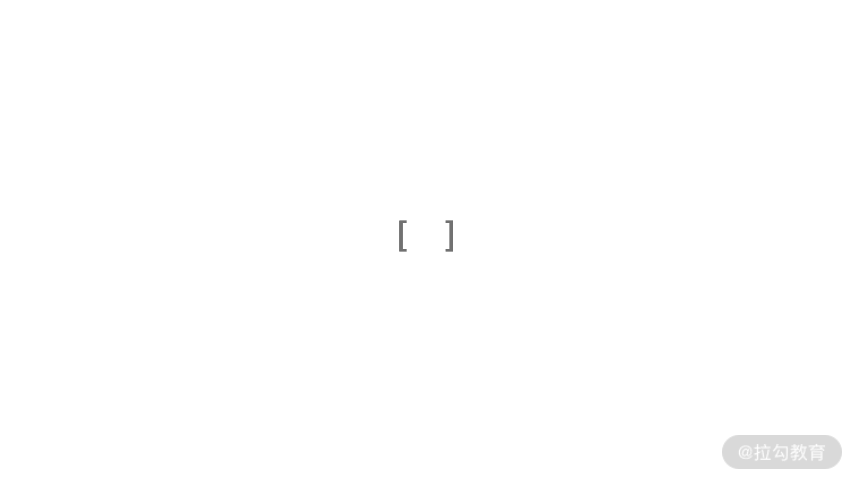
Step 1. 将元素 5 入队,元素 3,4 会被剔除掉。区间 [8,6,4,3,5] 最大值为队首元素 8。
Step 2. 将元素 8 出队,元素相等,直接出队。区间 [6,4,3,5] 最大值为队首元素 6。
Step 3. 将元素 6 出队,元素相等,直接出队。区间 [4,3,5] 最大值为队首元素 5。
Step 4. 将元素 4 出队,此时元素不等,队列不变。区间 [3,5] 最大值为队首元素 5。
Step 5. 将元素 3 出队,此时元素不等,队列不变。区间 [5] 最大值为队首元素 5。
Step 6. 将元素 5 出队,此时元素相等,直接出队。
可以发现,单调递减队列最重要的特性是:入队与出队的组合,可以在 O(1) 时间得到某个区间上的最大值。
前面说了利用单调队列可以得到某个区间上的最大值。可是这个区间是什么?怎么定量地描述这个区间?与队列中的元素个数有什么关系?
针对以上 3 个疑问,可以分两种情况展开讨论:
- 只有入队的情况
- 有出队与入队的情况
为了更直观地展示,我分别制作了两种情况对应的动图演示。先来看只有入队的情况,如下图所示:
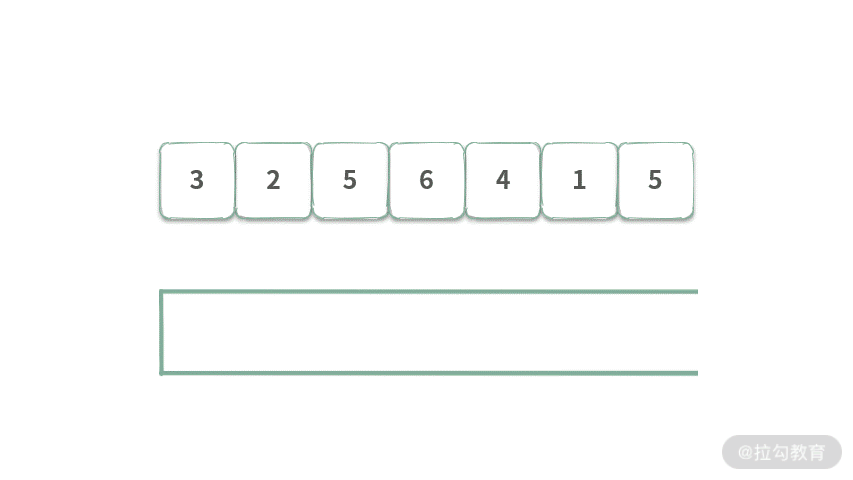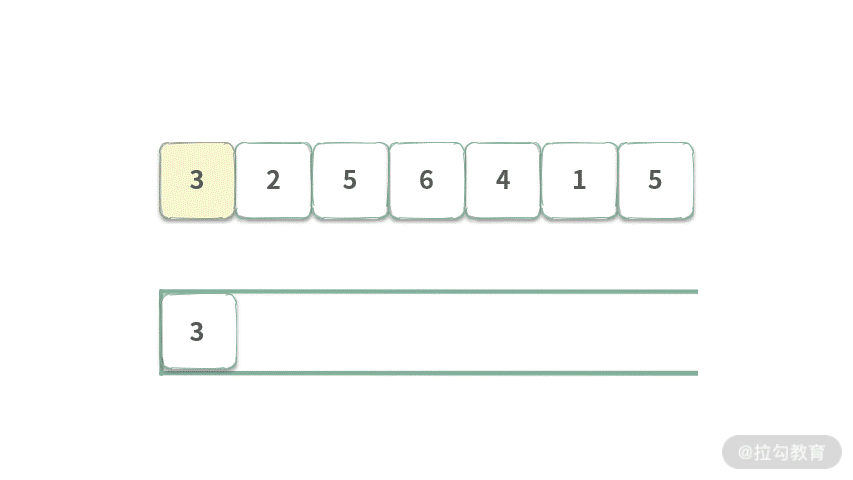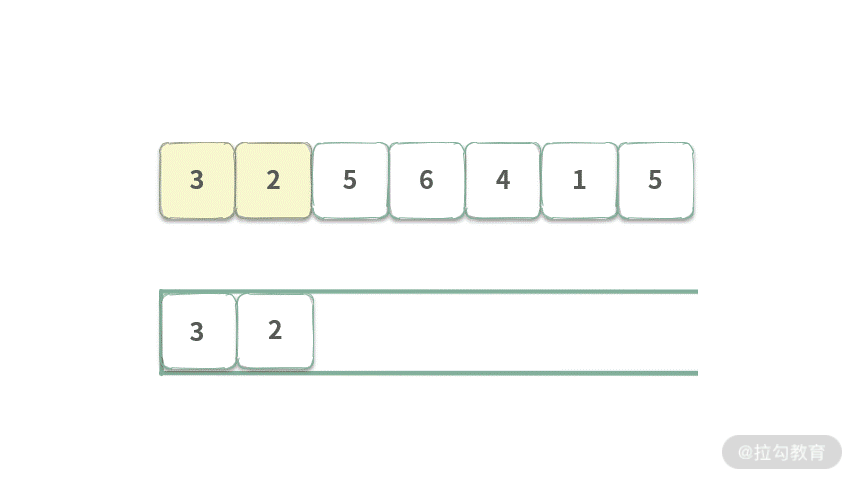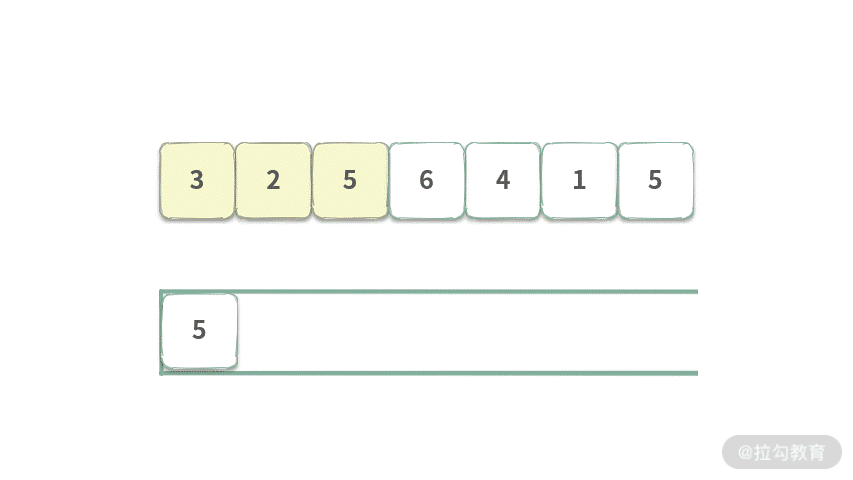
Step 1. 元素 3 入队,此时队首元素为 3,表示着区间[3]最大值为 3。
Step 2. 元素 2 入队,此时队列首元素为 3,表示区间[3,2]最大值为 3。
Step 3. 元素 5 入队,此时队首元素为 5,此时队列覆盖范围长度为 3,可以得到区间 [3,2,5] 最大值为 5。
继续执行入队,想必你也能得出结论了:在没有出队的情况下,黄色覆盖范围会一直增加,队首元素就表示这个黄色覆盖范围的最大值。
下面我们再来看出队与入队混合的情况。在上图 Step3 的基础上,如果再把 A[3] = 6 入队,这个时候,队列的覆盖范围长度为 4,假设我们想控制这个覆盖范围长度为 3,应该怎么办?
此时,我们只需要将 A[0] 出队即可。如下图所示:
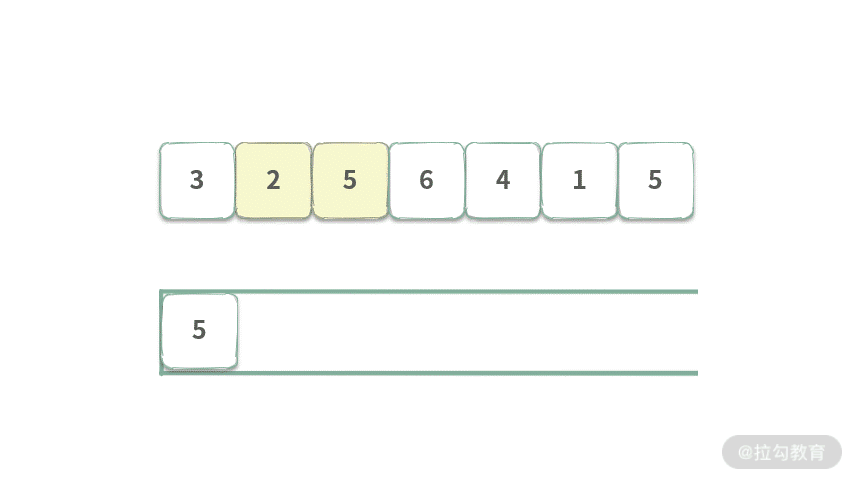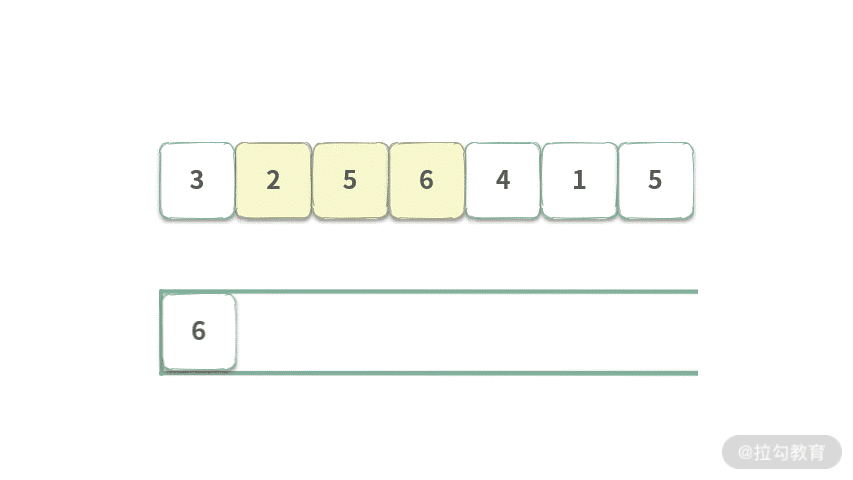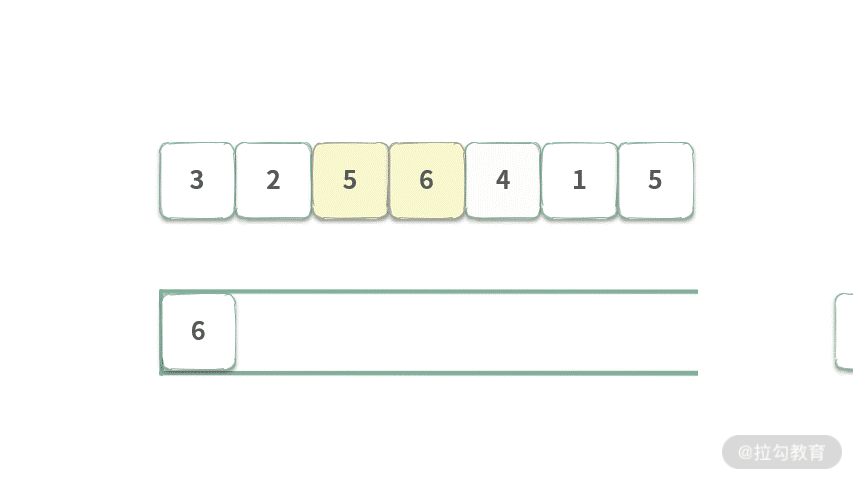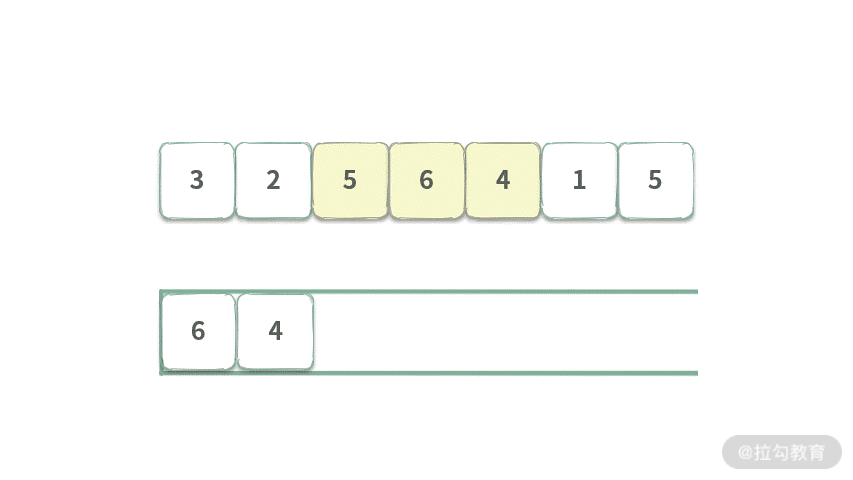
Step 4. 将元素 A[0] = 3 出队,由于此时 3 != Q.getFirst(),所以什么也不做。队列覆盖范围为 [2, 5],长度为 2。
Step 5. 将 A[3] = 6 入队,此时队首元素为 6,覆盖范围为[2,5,6],覆盖长度为 3,可以得到区间 [2,5,6] 最大值为 6。
Step 6. 将 A[1] = 2 出队,此时 2 != Q.getFirst(),所以什么也不做。此时队列覆盖范围为 [5, 6],长度为 2。
Step 7. 将 A[4] = 4 入队,此时覆盖范围为 [5, 6, 4],覆盖长度为 3,区间 [5,6,4] 最大值为 6。
从上图中可以发现以下几个重点:
- 入队,扩张单调队列的覆盖范围;
- 出队,控制单调递减队列的覆盖范围;
- 队首元素就是覆盖范围的最大值;
- 队列中的元素个数小于覆盖范围元素的个数。
这里,虽然我们只讨论了单调递减队列,实际上单调递增队列的特性也非常类似,你可以下来自己推导一下。下面我们深入到题目中,趁热打铁,把刚学到的知识运用起来。
例 3:滑动窗口的最大值
【题目】给定一个数组和滑动窗口的大小,请找出所有滑动窗口里的最大值。
输入:nums = [1,3,-1,-3,5,3], k = 3
输出:[3,3,5,5]
解释:
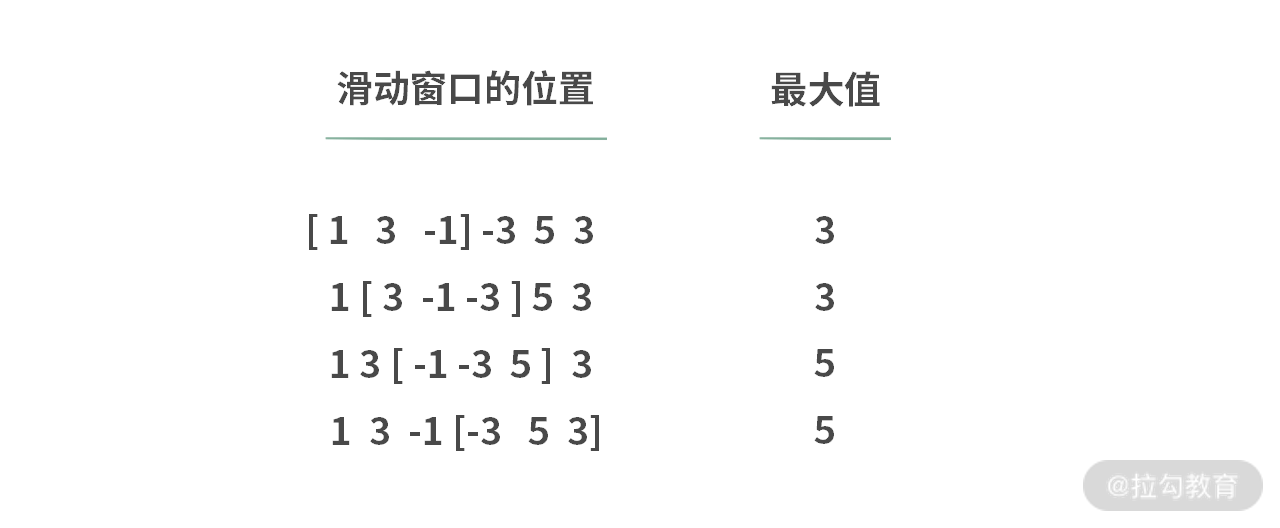
【分析】这是一道来自 eBay 的面试题。拿到时题目之后,可以发现,题目要求还是比较赤裸裸的,不妨先模拟一下,看看能不能想到比较好的解决办法。
1. 模拟
首先我们发现窗口在滑动的时候,有元素不停地进出。因此,可以采用队列来试一下。由于窗口长度为 3,所以将队列的长度固定为 3。
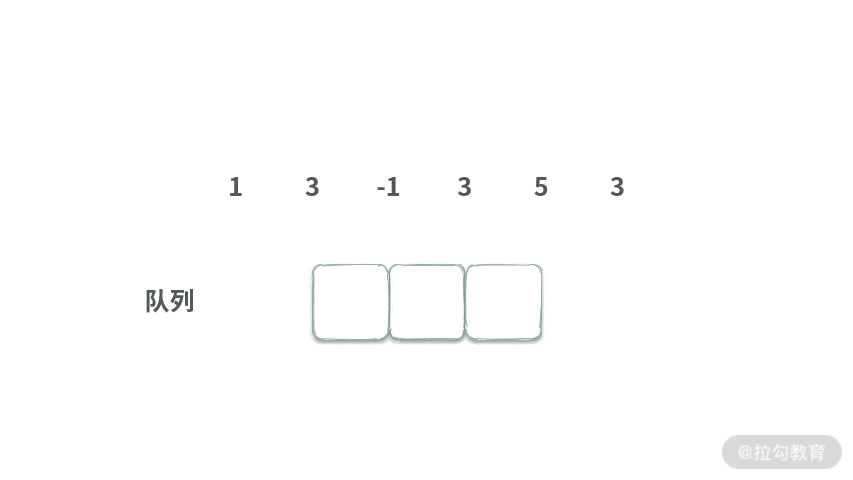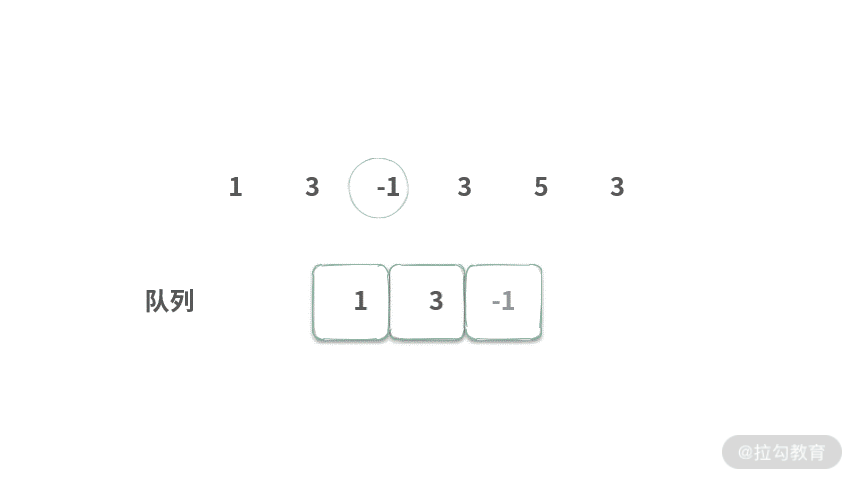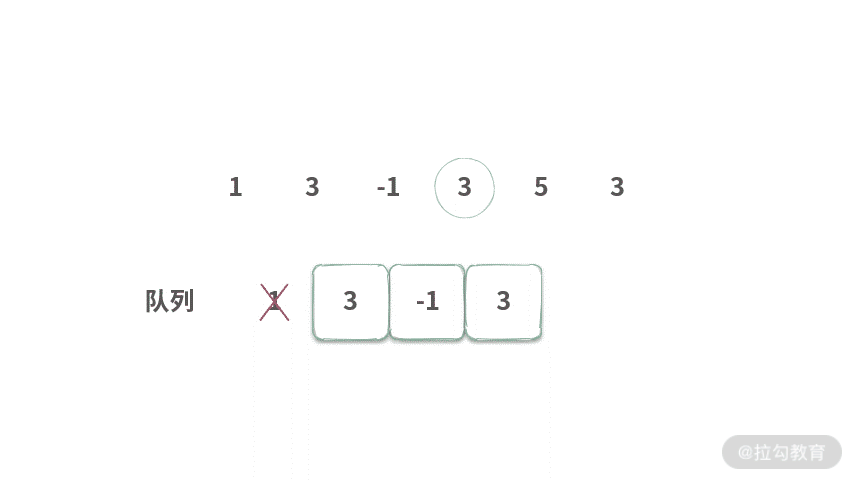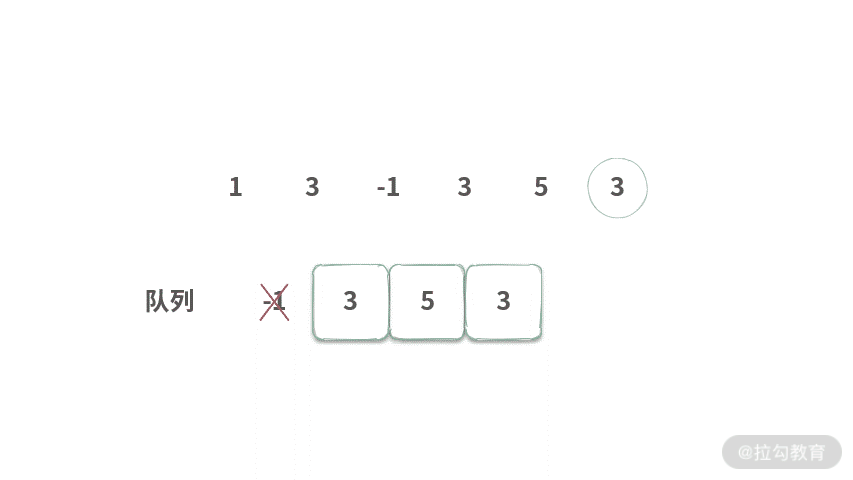
Step 1. 首先将元素 1 入队。
Step 2. 再将元素 3 入队。
Step 3. 再将 -1 入队,此时队列长度为 3,可以从 [1, 3, -1] 中得到最大值 3。
Step 4. 将 1 出队,然后将 3 入队,可以得到 [3,-1,3] 的最大值为 3。
Step 5. 将 3 出队,然后再将 5 入队,可以得到 [-1, 3, 5] 的最大值为 5。
Step 6. 将 -1 队出,然后再将 3 入队,可以得到 [3,5,3] 的最大值为 5。
2. 规律
我们发现两点:
(1)不停地有元素出队入队
(2)需要拿到队列中的最大值
如果能够在 O(1) 时间内拿到队列中的最大值,那么就可以在 O(N) 时间解决掉这个问题。
3. 匹配
到这里为止,已经匹配到了你学过的数据结构了——单调递减队列!
4. 边界
接下来,你可能准备开始写代码了,不过我还需要和你讨论一些细节与边界。
- 滑动窗口的大小与队列的大小。
- 哪种单调递减?为什么?
首先我们看窗口的大小。当使用 Q.getFirst() 时,得到的是整个队列的最大值,因此队列的大小,必须与滑动窗口的大小一样。也就是说,当 A[i] 入队的时候,A[i-k] 必须要出队!这样才能保证队列中的元素最多有 k 个。
虽然我们已经知道要使用单调递减队列求解这道题目了,但单调递减有两种:
- 严格单调递减(队列中没有重复元素)
- 单调递减
那么,应该用哪种呢?首先我们看一下严格单调递减是否可以工作,如下图所示:
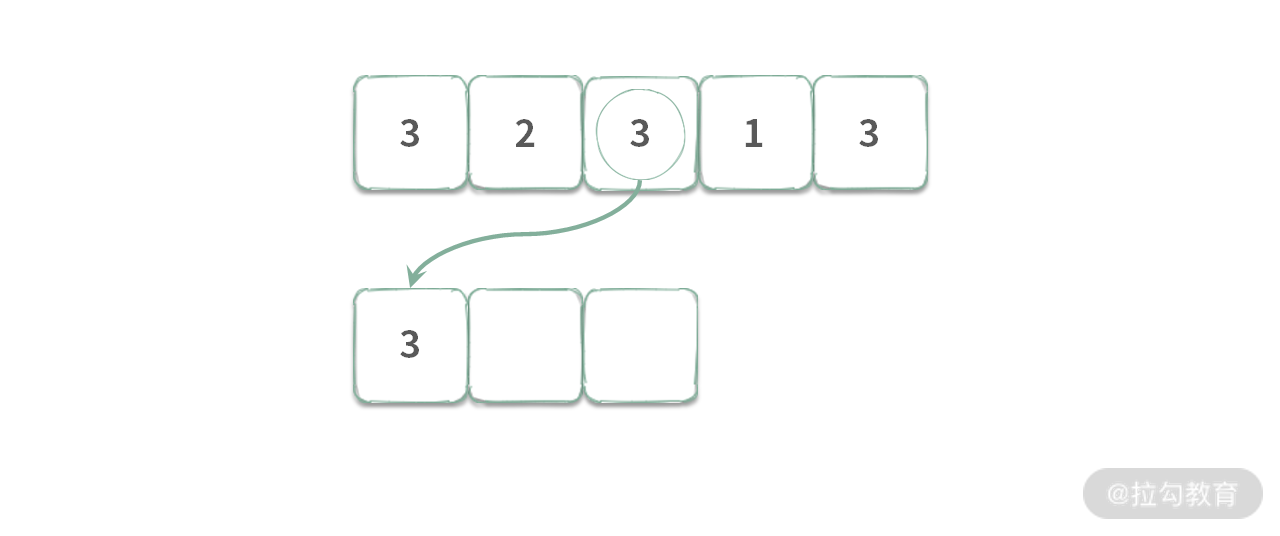
假设执行到 A[2] = 3 时,采用严格单调递减(队列中相等的元素也会被踢出去),入队时,A[2] 将会把所有的元素都踢出队列,队列变成 [3],那么可以得到 [3,2,3] 的最大值为 3。
但是由于窗口滑动的时候,接着需要把 A[0] = 3 出队,出队之后,队列为空。然后再将 A[3] = 1 入队得到。
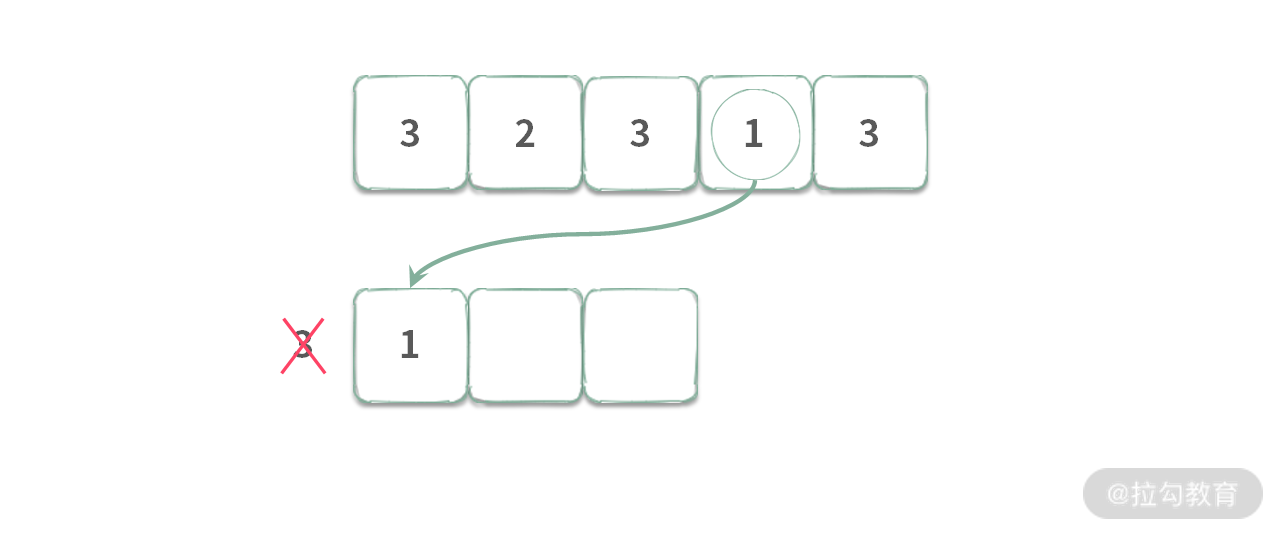
此时得到 [2,3,1] 的最大值为 1,这就出错了!所以我们不能使用严格单调递减队列求解。
注意:严格意义上来说,是可以使用严格单调递减队列,不过需要换一种出队方式,我会在例 4 讲解,在这里你可以先这么认为。
【画图】这部分运行过程与 “覆盖范围” 完全类似。经过前面的分析,现在你可以尝试自己画一下利用单调队列运行的过程图。如果你有什么疑问,可以在评论区留言,我们一起讨论。
【代码】现在我们已经分析清楚算法与数据结构,接下来就可以写代码了,代码如下(解析在注释里):
class Solution {private ArrayDeque<Integer> Q = new ArrayDeque<Integer>();private void push(int val) {while (!Q.isEmpty() && Q.getLast() < val) {Q.removeLast();}Q.addLast(val);}private void pop(int val) {if (!Q.isEmpty() && Q.getFirst() == val) {Q.removeFirst();}}public int[] maxSlidingWindow(int[] nums, int k) {List<Integer> ans = new ArrayList<>();for (int i = 0; i < nums.length; i++) {push(nums[i]);if (i < k - 1) {continue;}ans.add(Q.getFirst());pop(nums[i - k + 1]);}return ans.stream().mapToInt(Integer::valueOf).toArray();}}
复杂度分析:每个元素都只入队一次,出队一次,每次入队与出队都是 O(1) 的复杂度,因此整个算法的复杂度为 O(n)。
【小结】至此,我们已经学习了利用单调队列来解决滑动窗口的最大值。下面还可以扩展一下,比如:如何解决滑动窗口的最大值与最小值?具体你可以参考 “题目与代码”。
我们再对单调队列的特性做一下总结:
- 入队,扩展单调队列的覆盖范围
- 出队,缩小单调队列的覆盖范围
- 队首元素,是覆盖范围的最大值 / 最小值
- 范围内的最大值,需要用单调递减队列
- 范围内的最小值,需要用单调递增队列
单调队列在解决滑动窗口的最大值的时候,由于这个滑动窗口的大小是固定的。因此,单调队列的大小也是固定的。那么,你能不能用循环队列来模拟单调队列,求解滑动窗口最大值的题目呢?
例 4:捡金币游戏
【题目】给定一个数组 A[],每个位置 i 放置了金币 A[i],小明从 A[0] 出发。当小明走到 A[i] 的时候,下一步他可以选择 A[i+1, i+k](当然,不能超出数组边界)。每个位置一旦被选择,将会把那个位置的金币收走(如果为负数,就要交出金币)。请问,最多能收集多少金币?
输入:[1,-1,-100,-1000,100,3], k = 2
输出:4
解释:从 A[0] = 1 出发,收获金币 1。下一步走往 A[2] = -100, 收获金币 -100。再下一步走到 A[4] = 100,收获金币 100,最后走到 A[5] = 3,收获金币 3。最多收获 1 - 100 + 100 + 3 = 4。没有比这个更好的走法了。
【分析】这是一道来自头条的面试题。首先要纠正一种容易出错的想法:当走到 A[i] 的时候,选择 A[i+1, i+k] 里面的最大值作为下一步的落脚点。
如果是采用这种做法,那么根据示例会得到以下信息:
- 从 A[0] = 1 出发,收获金币 1。接下来面临的区间是 [-1, -100]。由于 -1 更大,所以选择 A[1] = -1 为落脚点;
- 从 A[1] = -1 出发,收获金币 -1。接下来面临的区间是 [-100, -1000],由于 -100 更大,所以选择 A[2] = -100 为落脚点;
- 从 A[2] = -100 出发,收获金币 -100。接下来面临的区间是 [-1000, 100],由于 A[4] = 100 更大,所以选择 A[4] = 100 为落脚点;
- 从 A[4] = 100 出发,收获金币 100,接下来走到 A[5] = 3;
- 停在 A[5] = 3,收获金币 3。一共收获金币 1 + (-1) + (-100) + 100 + 3 = 3。并不是最优的 4 个金币。
所以,这道题目,不能采用上述方法。下面我们利用 “四步分析法” 继续寻找更优解法。
1. 模拟
在分析题目时,一种办法是顺着题意走,另外一种办法是做假设。假设我们已经知道了走到 [0, i-1] 时收获的金币数目,用 get[] 数组来存放,那么走到 A[i] 最多可以收获的金币数目可以是下图这样:
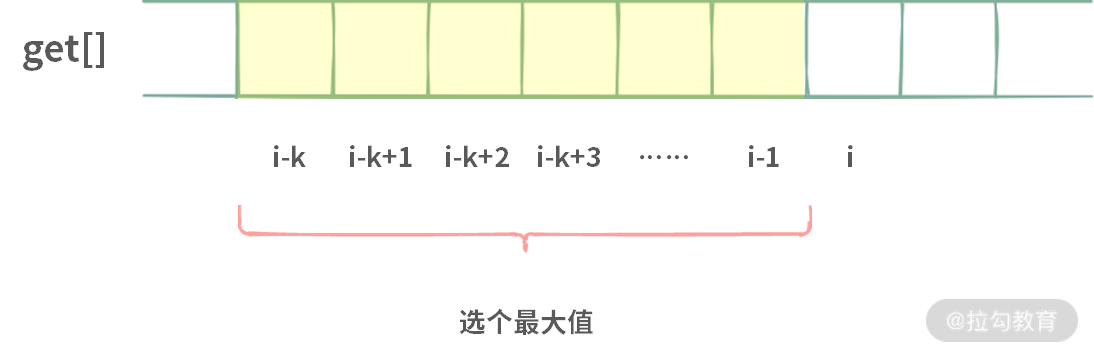
get[i] = max(get[i-k, ...., i-1]) + A[i]
考虑到 i - k 实际上可能会小于 0,对于这种情况,只需要取 max(0, i-k) 就可以了。
get[i] = max(get[max(i-k, 0), ...., i-1]) + A[i]
接下来采用上述方法来进行一波演算,以 [1,-1,-100,-100000,100,3], k = 2 为例,具体动图如下:
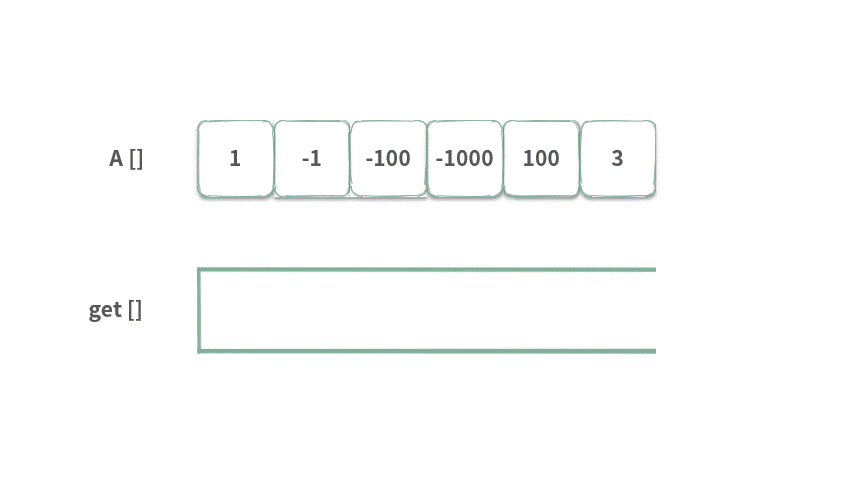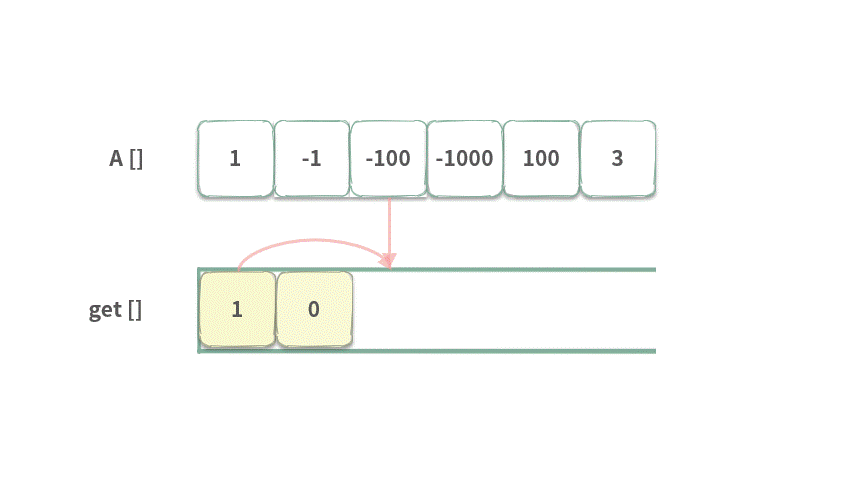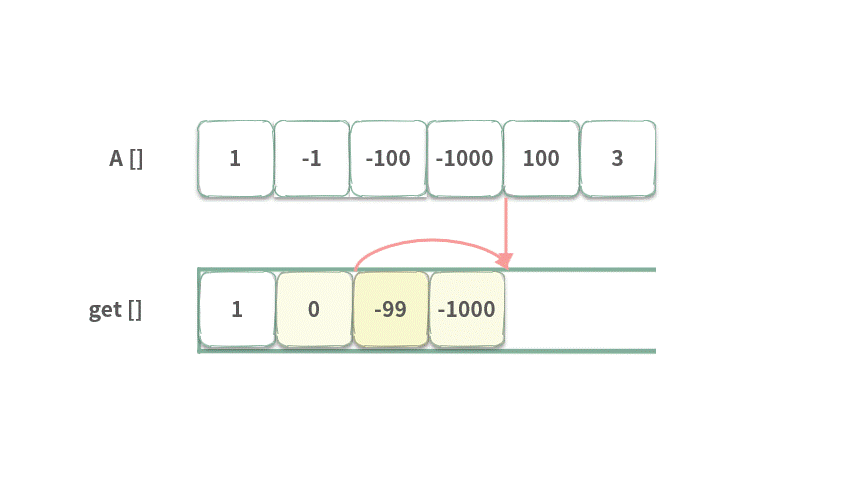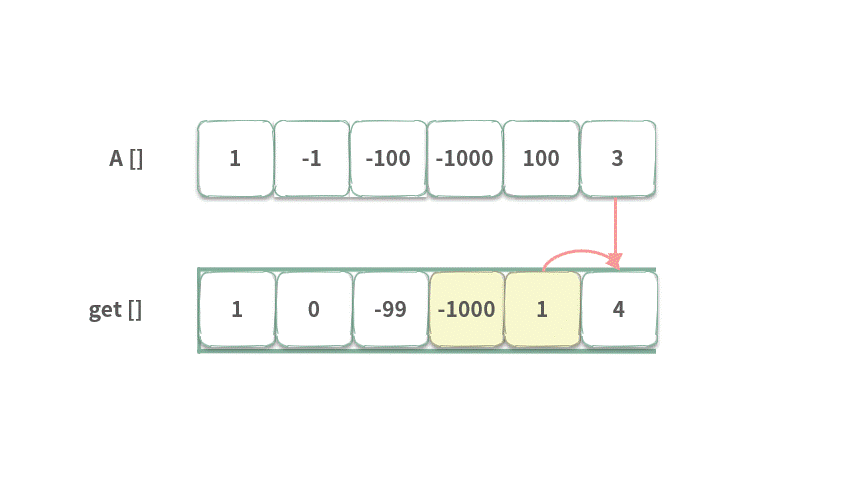
index = 0 时,前面没有元素,所以 get[0] = A[0]
index = 1 时,只有 get[0] 可以选。所以 get[1] = 1 + -1 = 0。
index = 2 时,前面有 get[0], get[1] 可以选,较大的数为 1,因此 get[2] = 1 - 100 = -99。
index = 3 时,前面有 get[1],get[2] 可以选,当然选较大的数 0 了。因此,get[3] = 0 - 1000 = -1000。
index = 4 时,前面有 get[2],get[3] 可以选。 当然选较大的数 get[2]。因此,get[4] = -99 + 100 = 1。
index = 5 时,前面有 get[3],get[4] 可以选。当然选较大的数 get[4]。因此,get[5] = 1 + 3 = 4。此时我们得到了最终答案 4。
2. 规律
经过模拟之后,我们发现,如果按照模拟的方法来写代码,那么复杂度会达到 O(Nk)。现在的问题是,每次要求 get[i] 的时候,都需要从前面长度为 k 的黄色范围里面选择一个最大值。有没有什么办法可以优化呢?
如果专注于黄色区域,会发现一个特点:黄色区域就是一个滑动窗口,我们要选的是滑动窗口的最大值。
3. 匹配
现在我们已经发现了滑动窗口,并且要求这个滑动窗口的最大值。那么数据结构已经呼之欲出了——单调队列。
4. 边界
这里要特别注意的是第一个元素 get[0]。此时单调队列为空。在求 get[0] 的时候,不能去单调队列中找最大值,要直接设置 get[0] = A[0]。
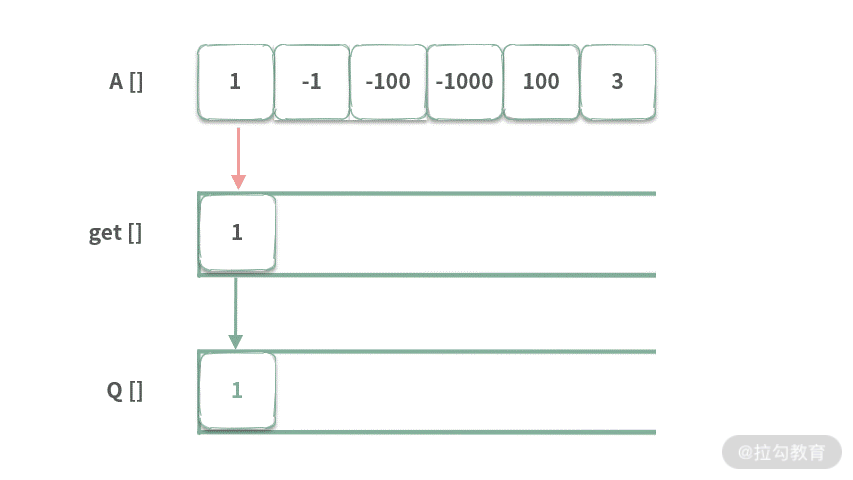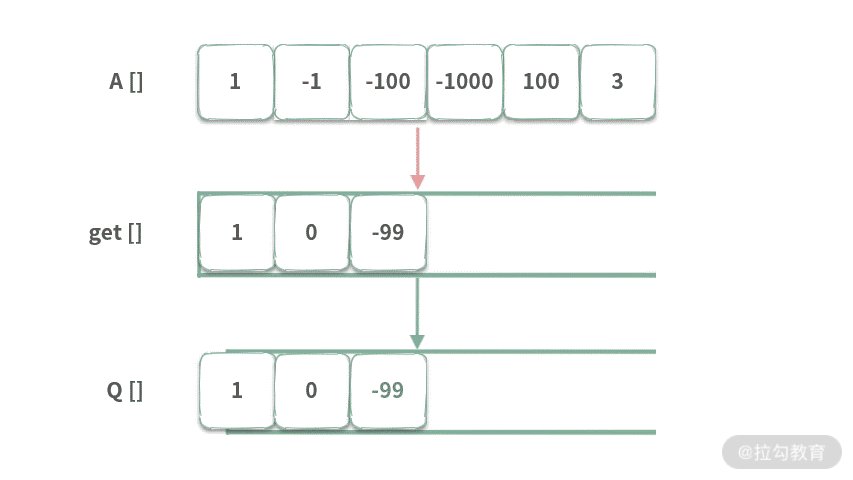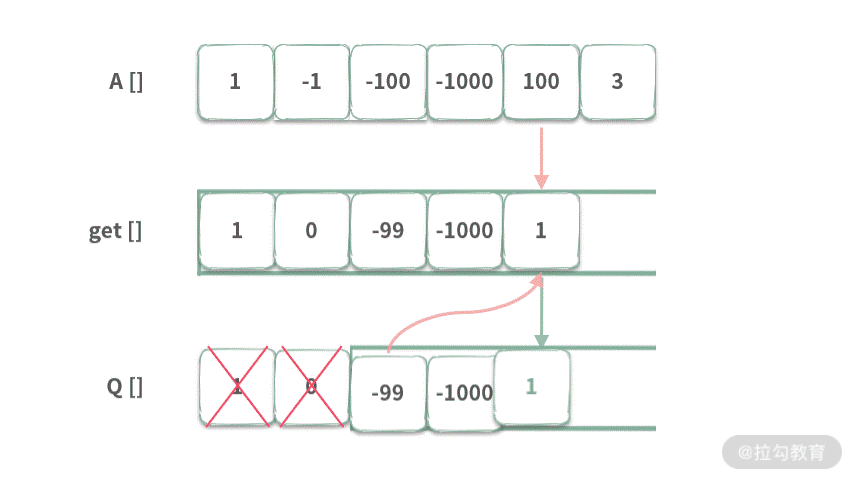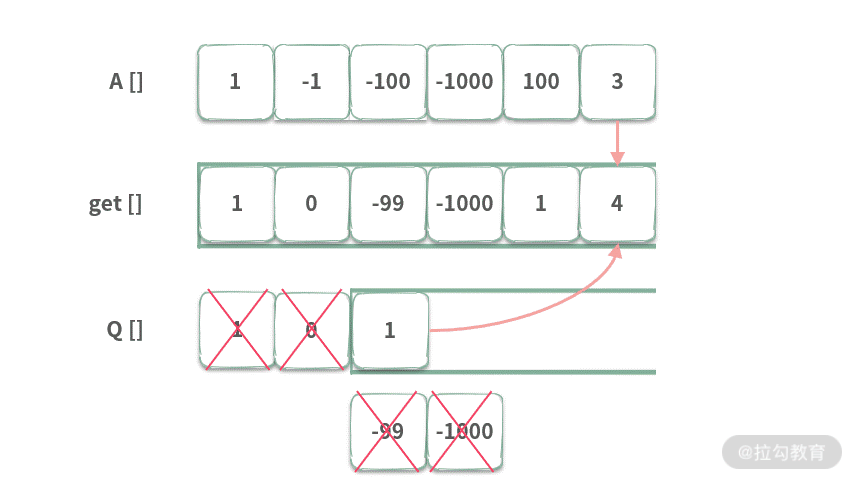
Step1. 当 index = 0 时,队列 Q[] 为空,那么 get[0] = A[0]。然后将 A[0] 入队。
Step 2. 当 index = 1 时,get[1] = 队首元素 + A[1] = 1 + -1 = 0。然后将 0 入队。
Step 3. 当 index = 2 时,get[2] = 队首元素 + A[2] = 1 - 100 = -99。然后将 -99 入队。
Step 4. 当 index = 3 时,首先将超出范围的元素出队。然后,get[3] = 队首元素 + A[3] = 0 - 1000 = -1000。然后将 -1000 入队。
Step 5. 当 index = 4 时,首先将队列中超出范围的元素出队,然后 get[4] = 队首元素 + A[4] = -99 + 100 = 1。然后再将 1 入队。
接下来我们重点看一下入队,由于 1 比队列中的元素都要大,按照单调队列的定义,所以队列中的元素都被清空。
Step 6. 当 index = 5 时,首先将队列中超出范围的元素出队(只不过此时队首元素和要出队的元素并不相等)。然后 get[5] = 1 + 3 = 4。
【代码】结合上述的讲解,写出代码如下(解析在注释里):
class Solution {public int maxResult(int[] A, int k) {if (A == null || A.length == 0 || k <= 0) {return 0;}final int N = A.length;int[] get = new int[N];ArrayDeque<Integer> Q = new ArrayDeque<Integer>();for (int i = 0; i < N; i++) {if (i - k > 0) {if (!Q.isEmpty() && Q.getFirst() == get[i-k-1]) {Q.removeFirst();}}int old = Q.isEmpty() ? 0 : Q.getFirst();get[i] = old + A[i];while (!Q.isEmpty() && Q.getLast() < get[i]) {Q.removeLast();}Q.addLast(get[i]);}return get[N-1];}}
复杂度分析:每个元素只入队一次,出队一次,每次入队与出队复杂度都是 O(n)。因此,时间复杂度为 O(n),空间复杂度为 O(n)。
【小结】这仍然是一个单调队列的题目。不同之处在于操作的时候,是通过了一个 get[] 数组来进行滑动窗口的。因此,这道题的考点就是两方面:
- 找到 get[] 数组,并且知道如何生成;
- 利用单调队列在 get[] 数组上操作,找到滑动窗口的最大值。
通过这道题你应该明白,有的时候,滑动窗口不一定是在给定的数组上操作,还可能会在一个隐藏的数组上操作。
拓展:是否存在不同的出队方式?
前面我们在学习单调队列的时候,利用了元素相等来判断是否出队。这种出队方式的特点是必须要保证单调队列不能是严格递减或者严格递增。
那么是否还有别的出队方式?是否可以不通过元素值相等的方式进行出队?针对上述两个问题,我们一起来看一下具体如何处理。
- 入队:入队的时候,将值和下标一起入队。
- 出队:直接判断队首元素的下标,进而判断是否应该将队首元素出队。
基于这种思想,我们可以将这道题换种写法。代码如下(解析在注释里):
class Solution {class Node {int sum = 0;int idx = 0;public Node(int s, int i) {sum = s;idx = i;}};public int maxResult(int[] A, int k) {ArrayDeque<Node> Q = new ArrayDeque<Node>();int ans = 0;for (int i = 0; i < A.length; i++) {while (!Q.isEmpty() && i - Q.getFirst().idx > k) {Q.removeFirst();}if (Q.isEmpty()) {ans = A[i];} else {ans = Q.getFirst().sum + A[i];}while (!Q.isEmpty() && Q.getLast().sum <= ans) {Q.removeLast();}Q.addLast(new Node(ans, i));}return ans;}}
复杂度分析:每个元素只入队一次,出队一次,每次入队与出队复杂度都是 O(n)。因此,时间复杂度为 O(n),空间复杂度为 O(n)。
总结与延伸
至此,你已经了解了单调队列的用法和特性。和 “第 01 讲” 一样,经过不断地 “浇灌”,我们又得到了一棵枝繁叶茂的 “大树”。回到知识层面,我把本讲重点介绍、且需要你掌握的内容总结在一张思维导图中,如下图所示:
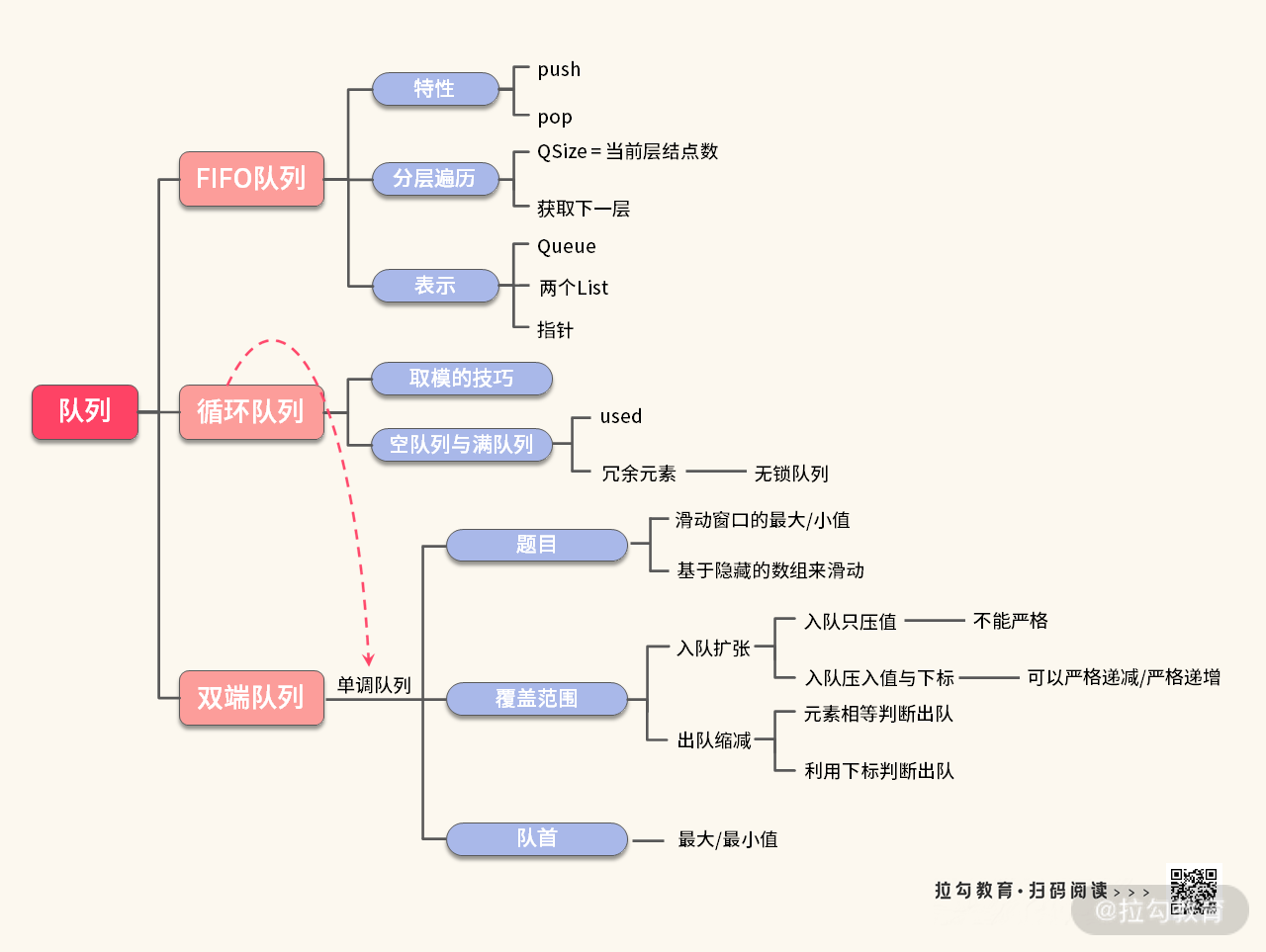
每个学科都会涉及很多知识,靠做题记知识点,就容易出现知识之间的割裂而形成孤立地,无法将知识系统化。希望你在做题的过程中能够主动尝试建立知识之间的联系,主动思考如何让新知识与原有知识相关联,提高学习效率。比如,循环队列实际上也是单调队列的好帮手,当然你也可以用来实现 FIFO 队列。
FIFO 队列和单调队列帮助我们解决了很多有趣的题目,通过这些题目,希望你能够整理出以下模板:
- 分层遍历
- 循环队列
- 单调队列
思考题
我再给你留一道思考题:在专栏的前两讲里学习了栈和队列,让我想到了曾经在面试中遇到过两道有意思的题目:
- 请利用栈来实现一个队列的操作
- 请用队列来实现一个栈的操作
你可以把答案写在评论区,我们一起讨论。接下来请和我一起踏上更加奇妙的算法与数据结构的旅程。让我们继续前进。
下一讲将介绍 03 | 优先级队列:堆与优先级队列,如何筛选最优元素。记得按时来探险。

