数据结构与算法面试宝典 - 前微软资深软件工程师 - 拉勾教育
今天我们开始学习一个非常有用的算法技能,排序。
排序在工程应用中有非常重要的作用,比如你随意点开一个搜索引擎,通过搜索得到的结果就是经过排序处理的;你参加互联网电商的秒杀活动,用户请求到达服务器之后,服务端程序会根据请求到达的时间进行排序处理。在数据库的设计中,字段的有序性也会影响我们的查询性能。
因此,面试中出现关于排序的算法题也就不足为奇了。但是,这里我们并不去介绍所有的排序算法,而是通过面试中最经常出现的两种排序算法进行深度展开。
- 合并排序
- 快速排序
学完本讲,你将收获相应的代码模板、排序的考点,以及排序在面试中的变化。现在,开始我们的算法旅程与探险!
合并排序
合并排序是将一个数组里面的元素进行排序的有效手段。它应该是在读书时学习的一个非常经典的排序算法了。不过这里我们不再采用教科书上的讲解方式,而是采用与 “二叉树” 进行结合的方式来学习。合并排序本质上与二叉树的后序遍历非常类似的。
如果你还能回想起来我们学习二叉树的时候,后序遍历有个重要的特点:拿到子树的信息,利用子树的信息,整合出整棵树的信息。
如果我们把有序性也当成信息,那么合并排序本质上就是一个后序遍历。这时新知识就和我们的旧知识产生了化学反应。合并排序的思路可以用二叉树表示如下:
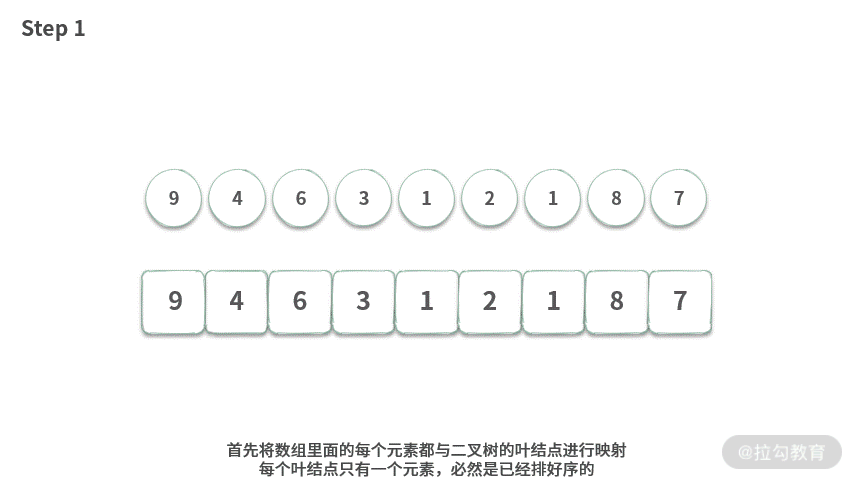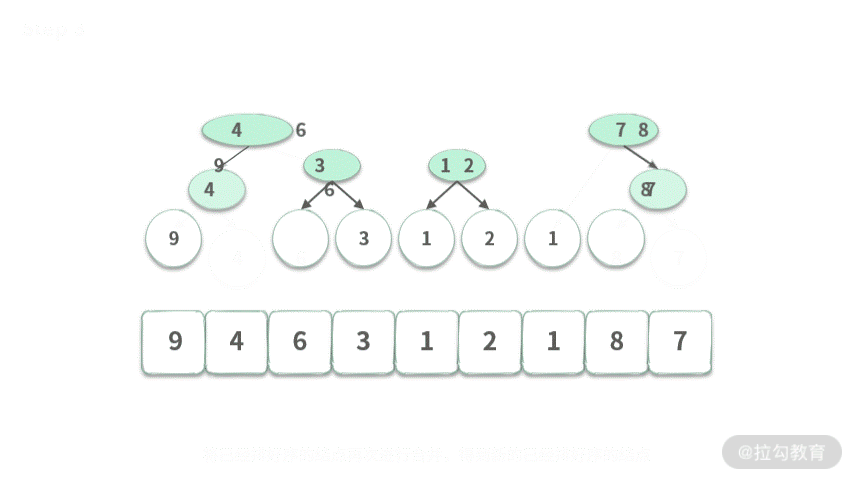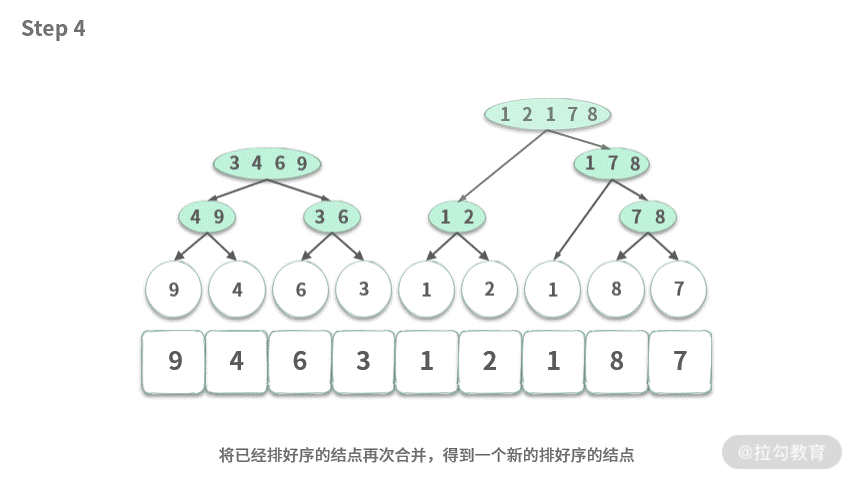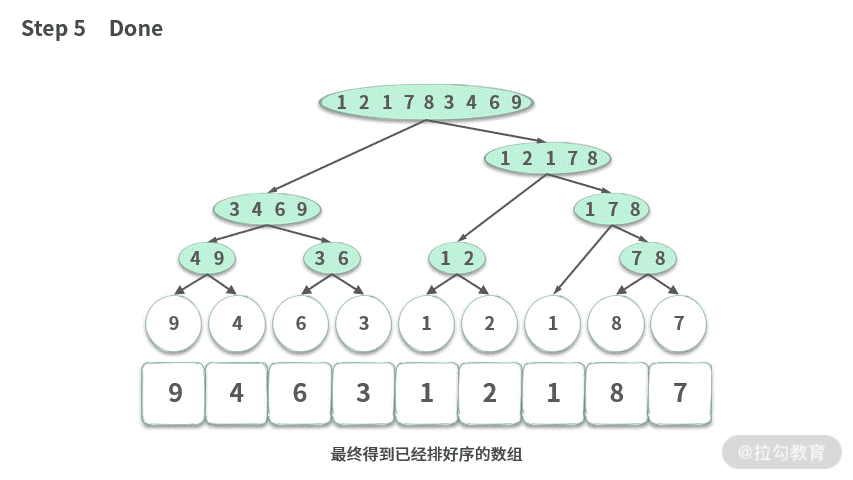
可以用伪代码表示如下:
function 后序遍历/合并排序():sub_info = 子结构(子树/子数组)full_info = 整合(sub_info)
那么合并排序 / 后序遍历的考点就可以总结为以下 3 点:
- 如何划分子结构
- 获取子结构的信息
- 利用子结构的信息,整合出整棵树的信息
我们可以把关联信息表达如下:
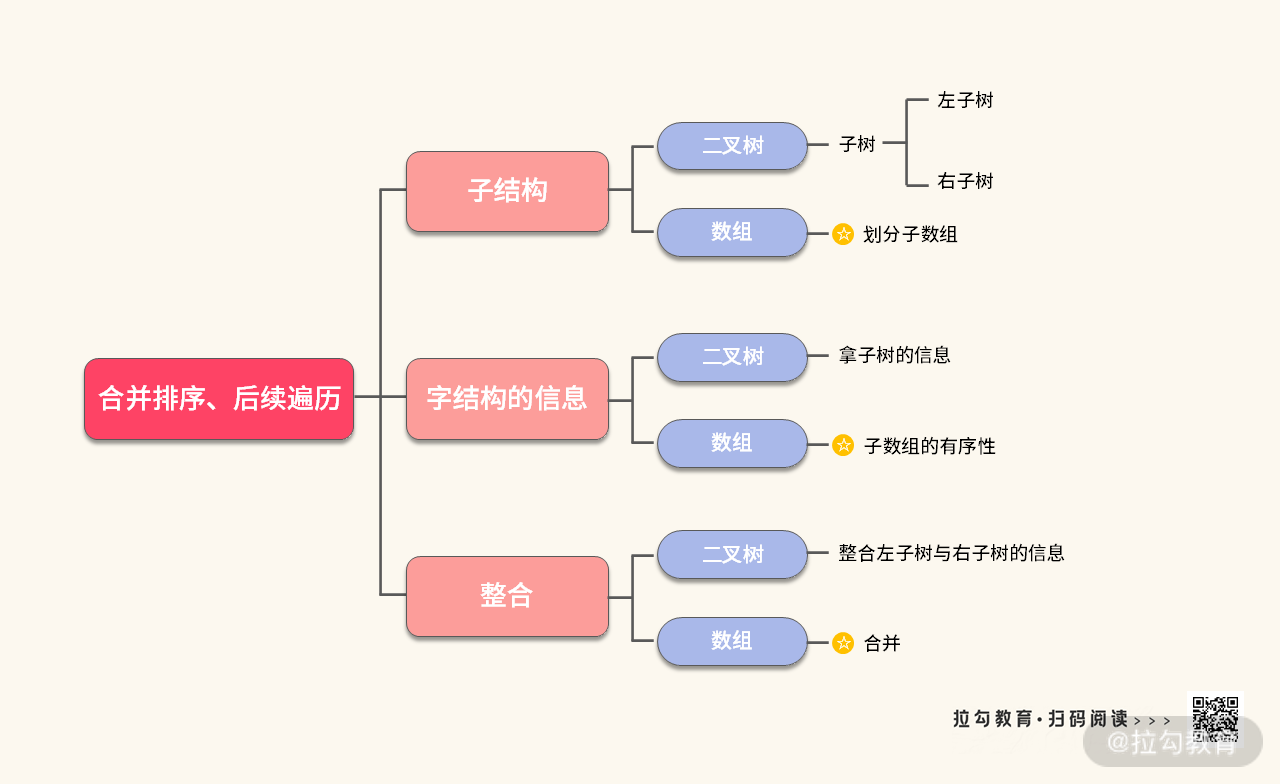
那么接下来我们就从这三方面入手。并且与二叉树的后序遍历的代码对照着一起看。
在正式开始讲题目之前,我们先学习一下开闭原则。实际上,绝大部分语言在设计的时候,都是按照这个原则。比如数组的第一个元素取下标 0,那么长度为 n 的数组,就需要用开闭原则区间 [0, n) 来表示。
这样表示好处理,区间长度直接就是右边界减去左边界。比如 [0, 10) 的区间长度就是 10。但是如果使用双闭区间,比如 [0, 9],那么求区间长度时,运行式为:9 - 0 + 1。还需要在减法的基础上加 1。
1. 划分
首先我们看一下如何划分子数组。对于二叉树而言,子树的划分是天然的,已经在数据结构里面约定好了,比如 TreeNode.left、TreeNode.right。
但是对于数组而言,在切分的时候,如果想到达最优的效率,那么将数组切为平均的两半效率应该是最高的(可以联想到二叉平衡树的效率)。为了帮助你理解,我绘制了动图演示,如下所示:
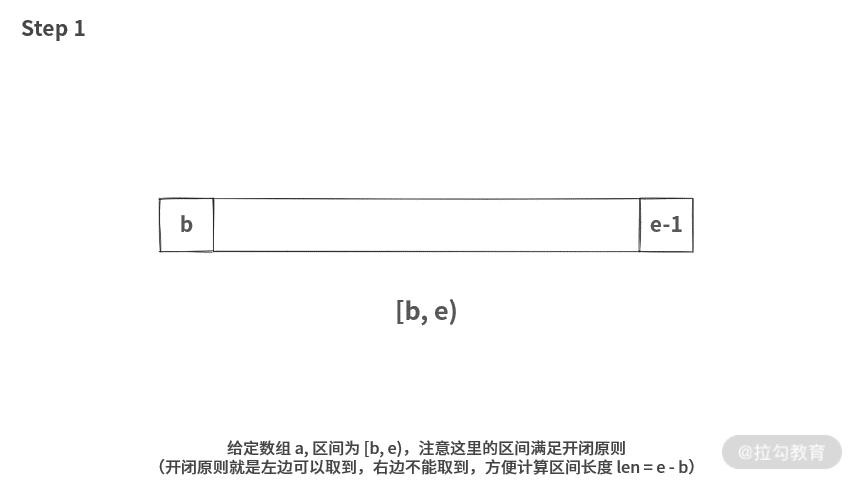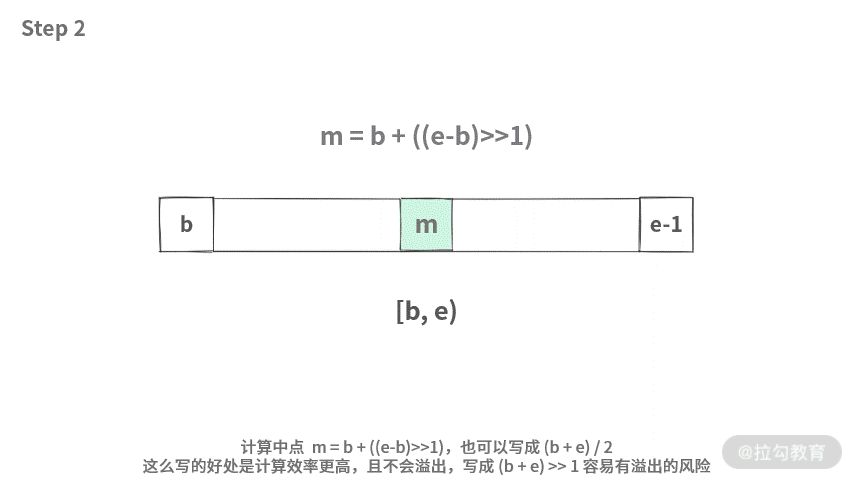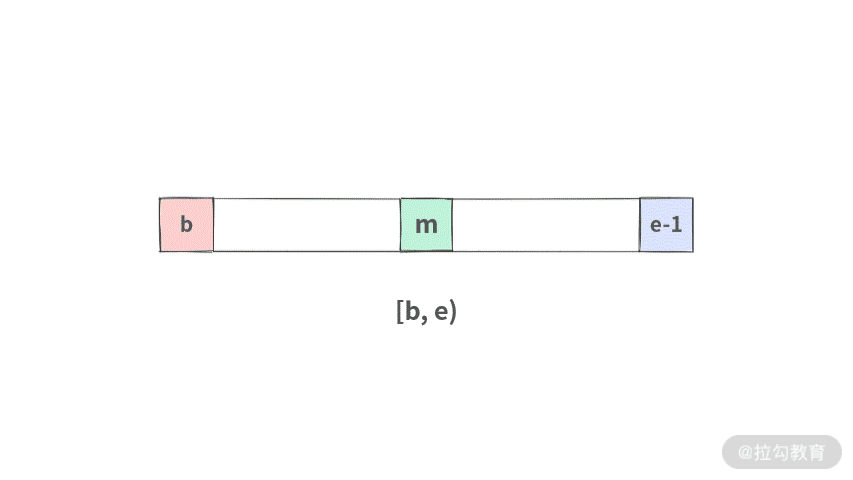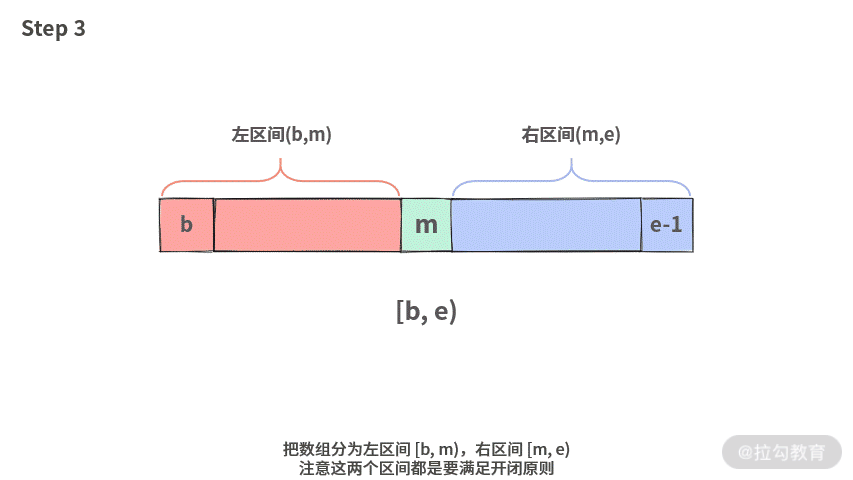
二叉树的写法如下:
root.left, root.right; 可以直接通过root的结构体信息得到。
合并排序的写法如下:
final int m = b + ((e-b)>>1);数组a, [b, m) => 表示左子数组。数组a, [m, e) => 表示右子数组。需要通过计算得到。
2. 子数组的信息
由于这里是排序,那么就分别需要对左子数组和右子数组进行排序。如果你还能想起来我们在 “第 06 讲” 介绍过的 “二叉树的后序遍历”,那么对子数组的排序,只需要递归就可以了。
postOrder(root.left);postOrder(root.right);
合并排序则需要这样写:
merge_sort(a, b, m);merge_sort(a, m, e);
3. 信息的整合
接下来,我们需要将从子树 / 子数组里面拿到的信息进行加工。不同的需求会导致加工的方式也不太一样。对于合并排序而言,我们需要将两个有序的子数组,合并成一个大的有序的数组。
最后,还需要考虑一下边界:
- 当 b >= e,说明这个区间是一个空区间,没有必要再排序;
- 当 b + 1 == e,说明只有一个元素,也没有必要排序。
以上两种边界情况分别可以对应到当二叉树为空,以及二叉树只有一个结点的情况。
【代码】到这里,我们已经可以写出合并排序的代码了(解析在注释里):
class Solution {private void msort(int[] a, int b, int e, int t[]) {if (b >= e || b + 1 >= e) {return;}final int m = b + ((e - b) >> 1);msort(a, b, m, t);msort(a, m, e, t);int i = b;int j = m;int to = b;while (i < m || j < e) {if (j >= e || i < m && a[i] <= a[j]) {t[to++] = a[i++];} else {t[to++] = a[j++];}}for (i = b; i < e; i++) {a[i] = t[i];}}public void mergeSort(int[] nums) {if (nums == null || nums.length == 0) {return;}int[] t = new int[nums.length];msort(nums, 0, nums.length, t);}}
复杂度分析:时间复杂度 O(NlgN),空间复杂度 O(N)。
【小结】这里我们归纳一下合并排序的考点:
- 如何切分左右子数组;
- 如何进行合并,合并时注意循环的条件,以及稳定排序的写法;
- 开闭原则。
所以解决这道题目的考点可以总结如下:
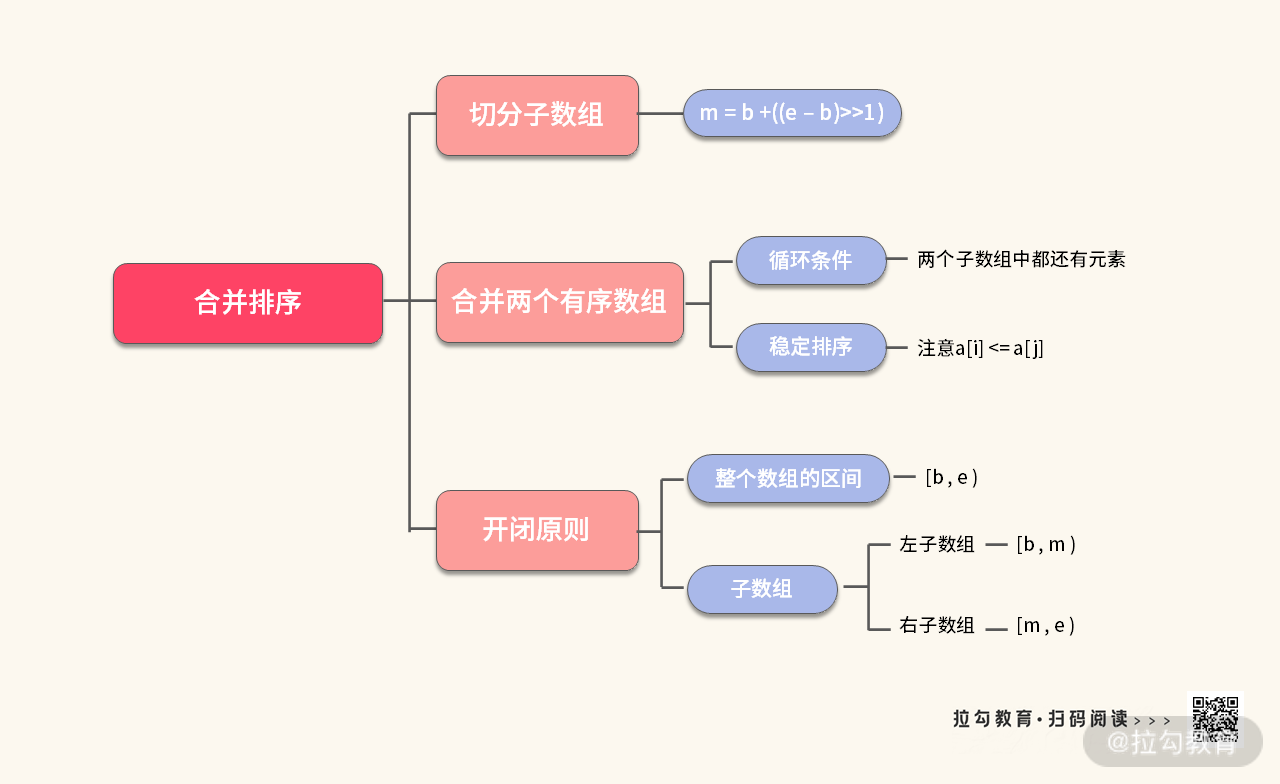
拓展思路:如果你已经成功获得了合并排序的秘籍,那么可以进一步尝试一下解决链表的合并排序。
思考题:给定一个链表,如何排序,使其时间复杂度能够达到 O(NlogN)。空间复杂度为 O(1)。小提示:会用到合并排序,以及前面介绍的链表小技巧。
我们还注意到:排序与二叉树的后序遍历联系在一起了。在 “第 06 讲” 中我们提到过,后序遍历有一个非常有趣的用法就是 “项庄舞剑,意在沛公”,那么合并排序是不是也有同样的性质呢?
当然可以了,那么接下来,我们利用合并排序再玩一下这个套路。
例 1:逆序对
【题目】一个整数数组,当 a[i] > a[j],并且 i < j 的时候,(a[i], a[j]) 构成一个逆序对。求一个数组中逆序对的数目。
输入:[1, 2, 3, 4, 0]
输出:4
解释:数字 0 会和前面的每一个数构成逆序对。一共有 4 对。所以输出 4。
【分析】我们打算用合并排序解决这个问题。其中,合并排序提供的信息是 “有序性”,那么我们就找到了 “项庄”——有序性。而我们真正要求解的是 “逆序对”,所以 “沛公” 也找到了。
下面我们回顾一下 “第 06 讲” 学习后序遍历的时候,我们总是利用左右子树的信息进行整合,进而得到 “沛公”。对于合并排序而言,当得到有序的左右子数组之后,应该怎么得到逆序对信息呢?
这里我们用画图来表示一下:
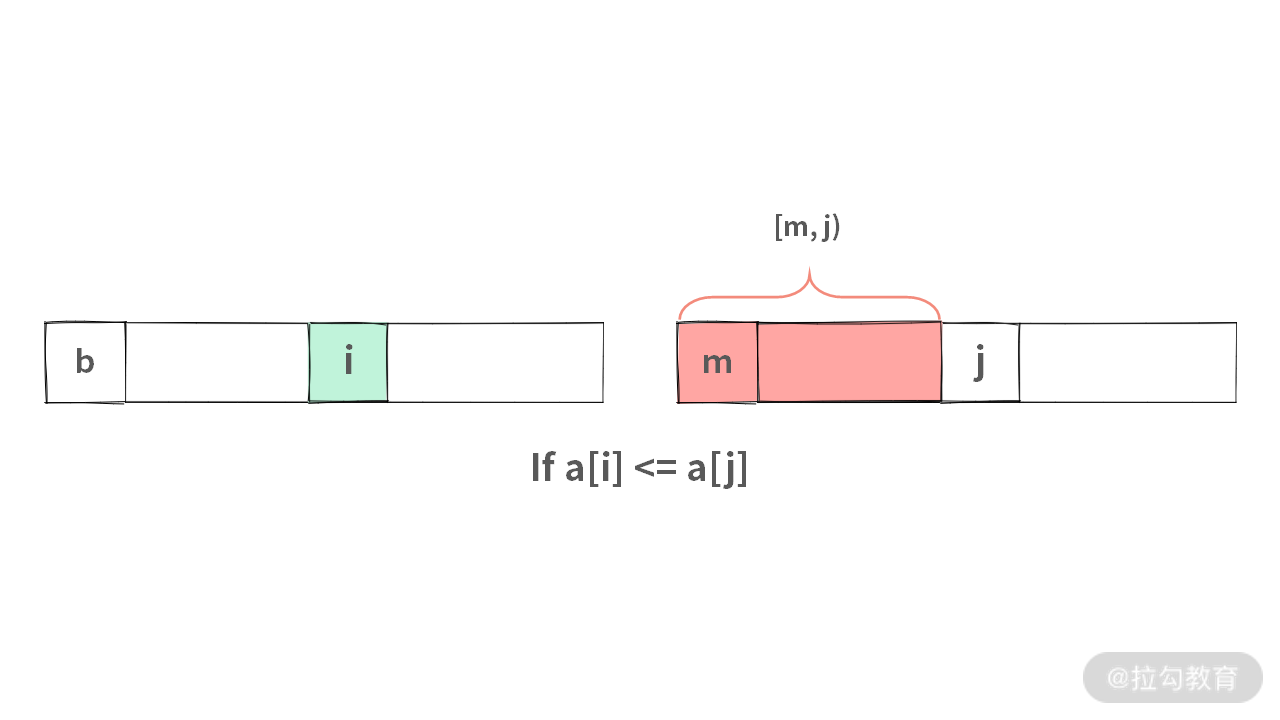
当两个有序的子数组合并的时候,如果 a[i] <= a[j],此时应该执行 t[to++] = a[i++]。那么左子数组的 [b, i),以及右子数组 [m, j) 里面的元素肯定都在 a[i] 之前就被合并掉了。
由于 a[i] 在左子数组,所以 a[i] 与 [m, j) 这个范围里面的元素就构成逆序对。 因此,在此时可以得到的逆序对的数目需要加上 j - m。
【代码】到这里我们就一起来写一下代码吧(解析在注释里):
class Solution {private int cnt = 0;private void msort(int[] a, int b, int e, int[] t) {if (b >= e || b + 1 >= e) {return;}final int m = b + ((e - b) >> 1);msort(a, b, m, t);msort(a, m, e, t);int i = b;int j = m;int to = b;while (i < m || j < e) {if (j >= e || i < m && a[i] <= a[j]) {t[to++] = a[i++];cnt += j - m;} else {t[to++] = a[j++];}}for (i = b; i < e; i++) {a[i] = t[i];}}public int reversePairs(int[] nums) {if (nums == null || nums.length <= 1) {return 0;}int[] t = new int[nums.length];cnt = 0;msort(nums, 0, nums.length, t);return cnt;}}
【小结】我们再总结一下合并排序的特点和用法。关于逆序对这道题目,还可以做一个小更改:求解拿到顺序对的数目。开动你的聪明大脑想一想吧!你可以把想法写在留言区,我们一起交流。
接下来我们再从求逆序对那句关键的代码进行展开:
if (j >= e || i < m && a[i] <= a[j]) {t[to++] = a[i++];cnt += j - m;}
由上述代码可以得知,这里求出来的逆序对是属于 a[i] 的,根据前面的分析,我们可以拓展出下面这道思考题。
深度扩展:给定一个数组 A[],你能够返回一个数组 ans[],ans[i] 存放 A[i] 的逆序对数目。如果做出来这道题目,你能想一下增加的考点和变化是什么吗?可以写在留言区哦。
接下来我们看一下广度扩展。
例 2:找出两个有序数组的中位数
【题目】给定两个有序数组,请找出这两个有序数组的中位数。
输入:A = [1, 2], B = [3, 4]
输出:(2 + 3) / 2 = 2.5
解释:当个数为奇数时,取排序之后的中间那个数。当个数为偶数时,取排序后中间两个数的平均值。
【分析】这是一道来自百度的面试题。解法有很多,我们重点介绍基于合并模板的解法。
通过合并排序,我们已经能够将两个有序的数组合并成一个有序的数组了。合并是一个非常经典的模板代码,你一定要理解并且背下来,很多地方都会用。比如合并有序链表,合并数组。
你可能会想到直接将两个有序数组合并成一个有序的数组,再取这个有序数组的中位数。但是这样操作的话,时间复杂度就变成 O(N),并且空间复杂度也是 O(N)。
如果在面试现场,面试官一定会问你,有没有更好的办法?所以我们应该有效地利用两个数组的有序性解决这道题。下面我会从简单的情况开始分析。
首先我们看一维有序数组的情况,如果我们要拿第 5 小的数。(注:第 1 小就是最小的数。)只需要将前面 4 个数扔掉,然后排在前面的数就是第 5 小的数。
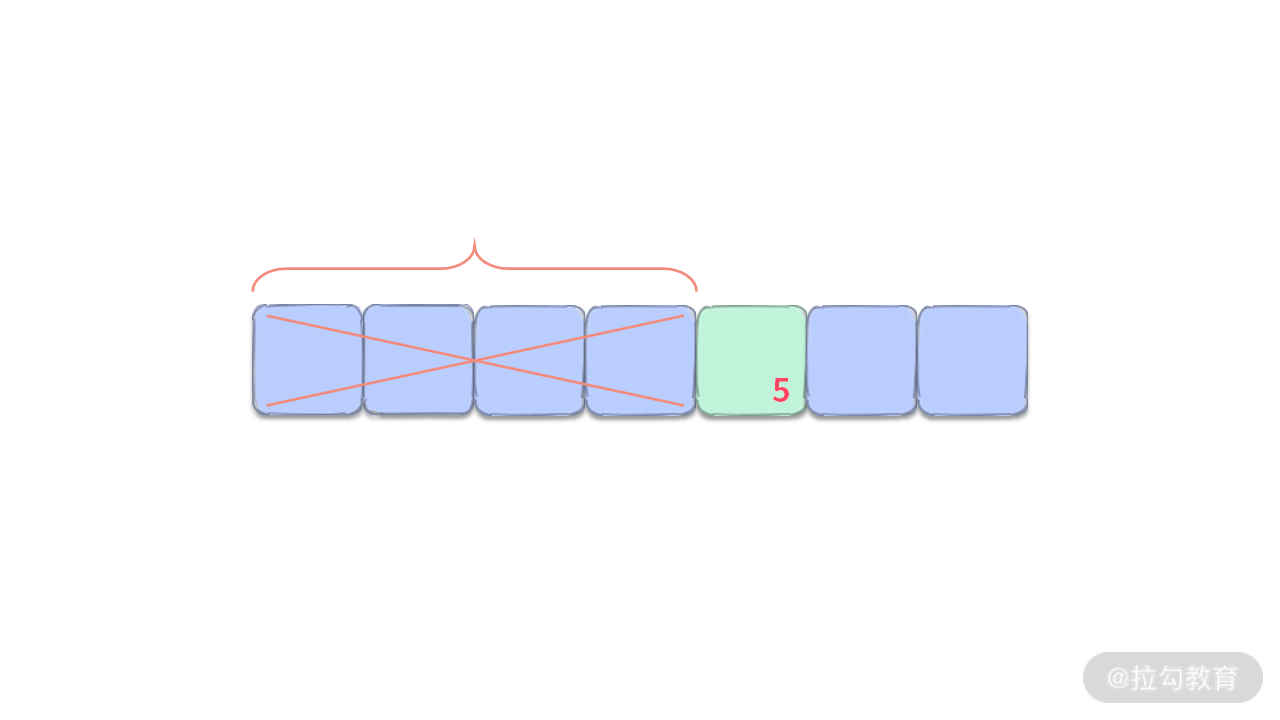
那么二个有序数组应该怎么办呢?不过现在非常确定的是,我们一定会扔掉 4 个数。那么接下来,你再思考一下在两个数组 A,B 中如何扔掉这 4 个数?
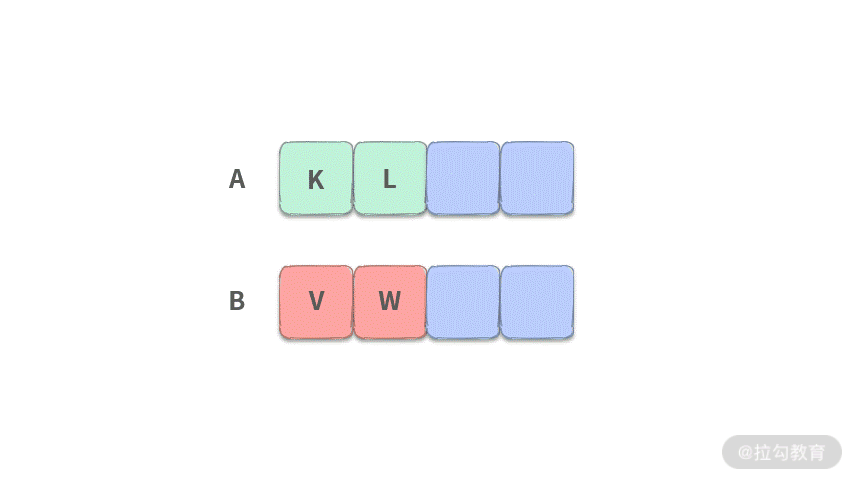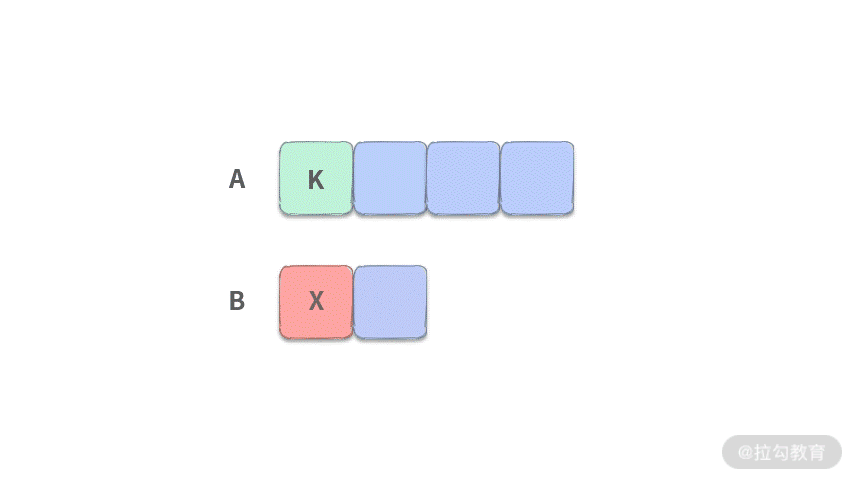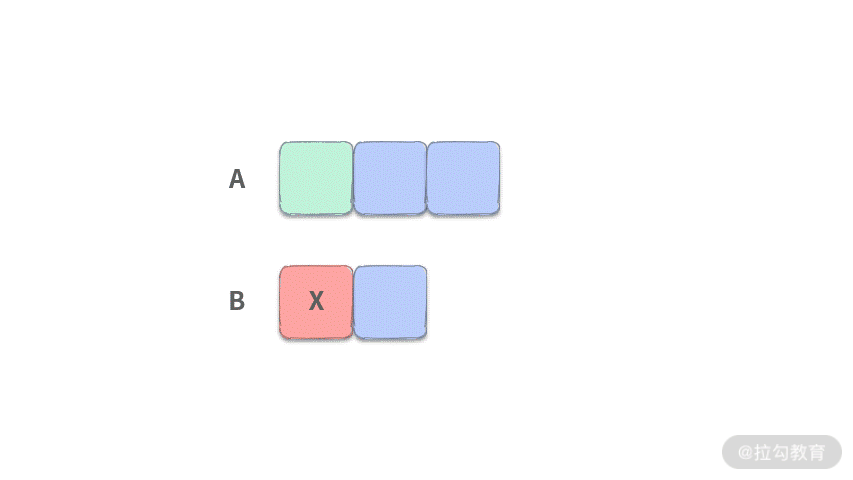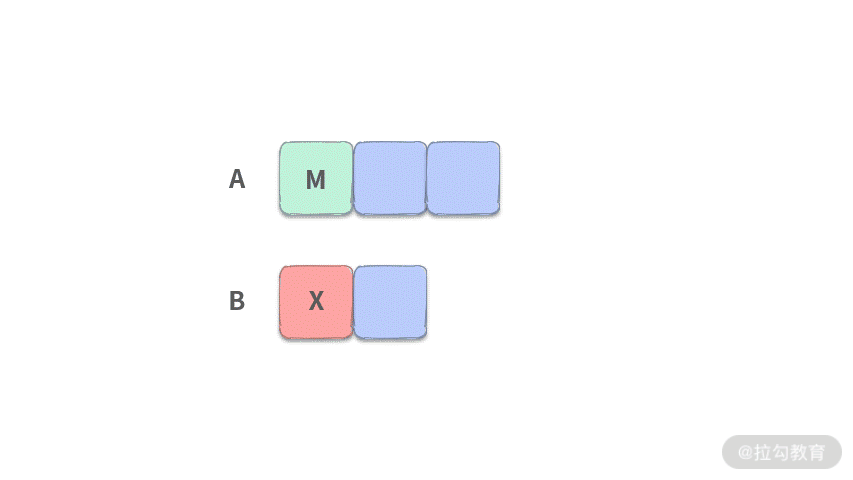
- 第 1 步:要扔掉 4 个数,我们需要看一下两个数组前 2 个元素,如下图所示:
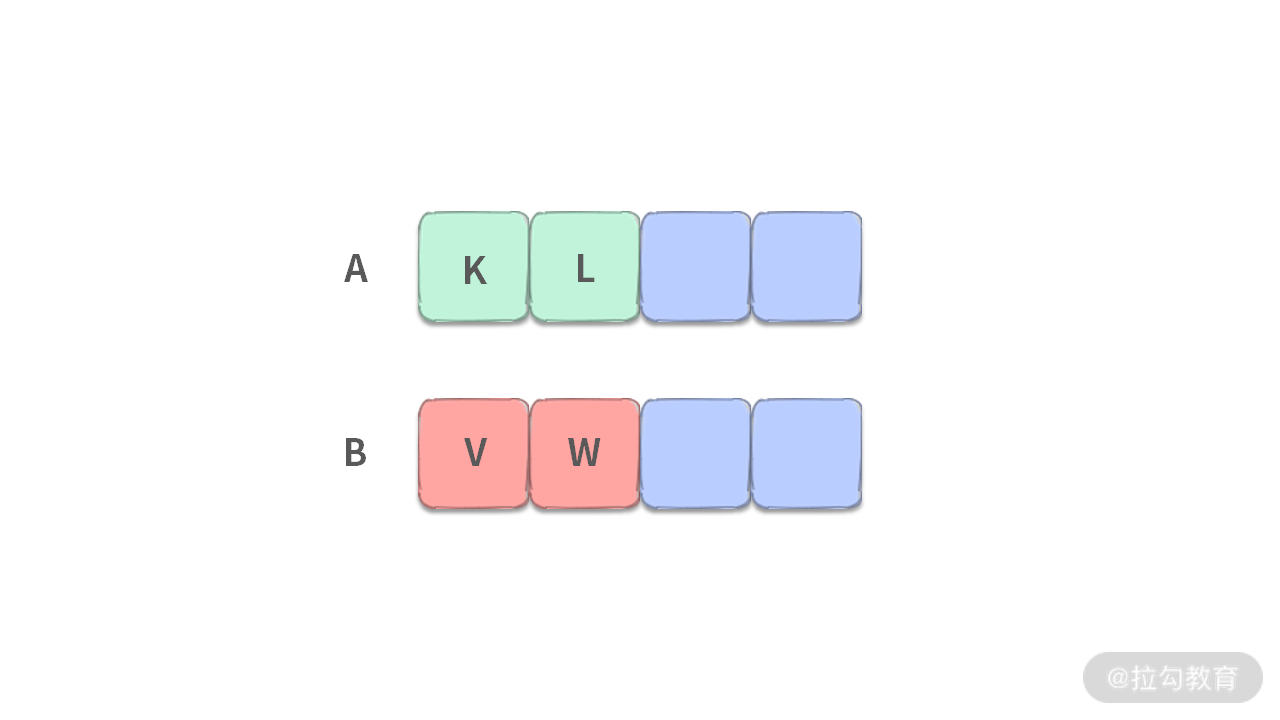
此时,我们当然不知道 K、L、V、W 这四个数之间的关系。假设 L >= W,就需要证明:当 L >= W 的时候,[V, W] 都不可能是第 5 小的数,可以扔掉。
解:利用反证法,假设 W 可以成为第 5 小的数。推导过程如下:
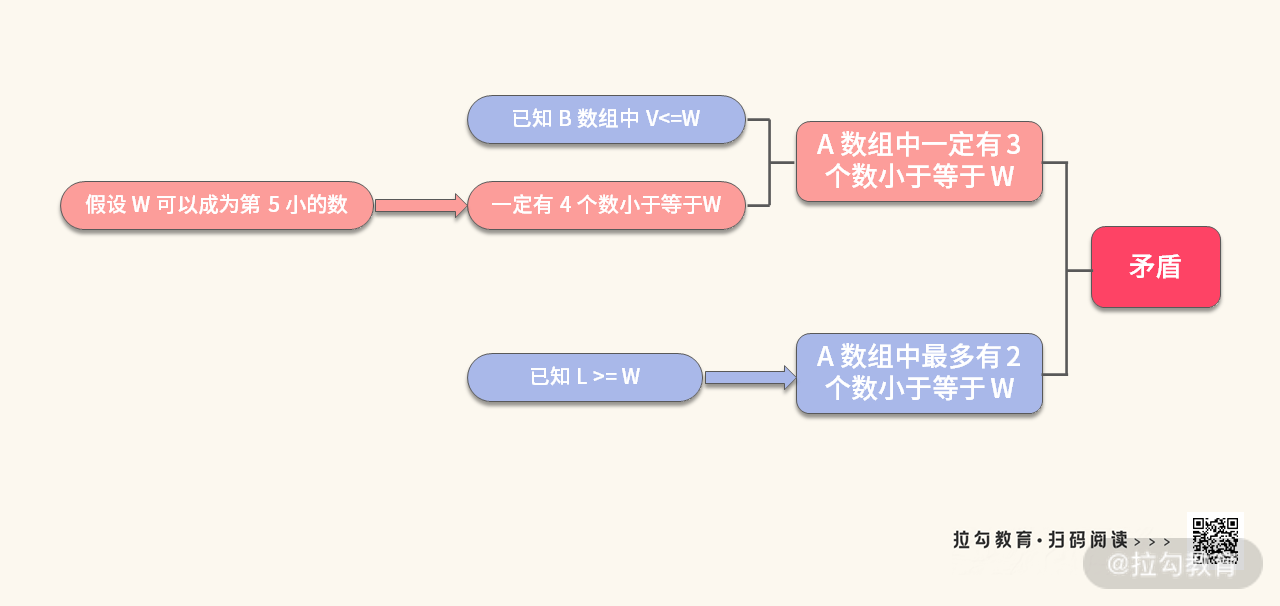
同样的方法可以证明,V 也不可能成为第 5 小的数。所以如果当 L>=W 的时候,可以把 [V, W] 扔掉,不影响去拿第 5 小的数。
- 第 2 步:当我们扔掉 2 个数之后,两个有序数组已经变成如下图所示的样子:
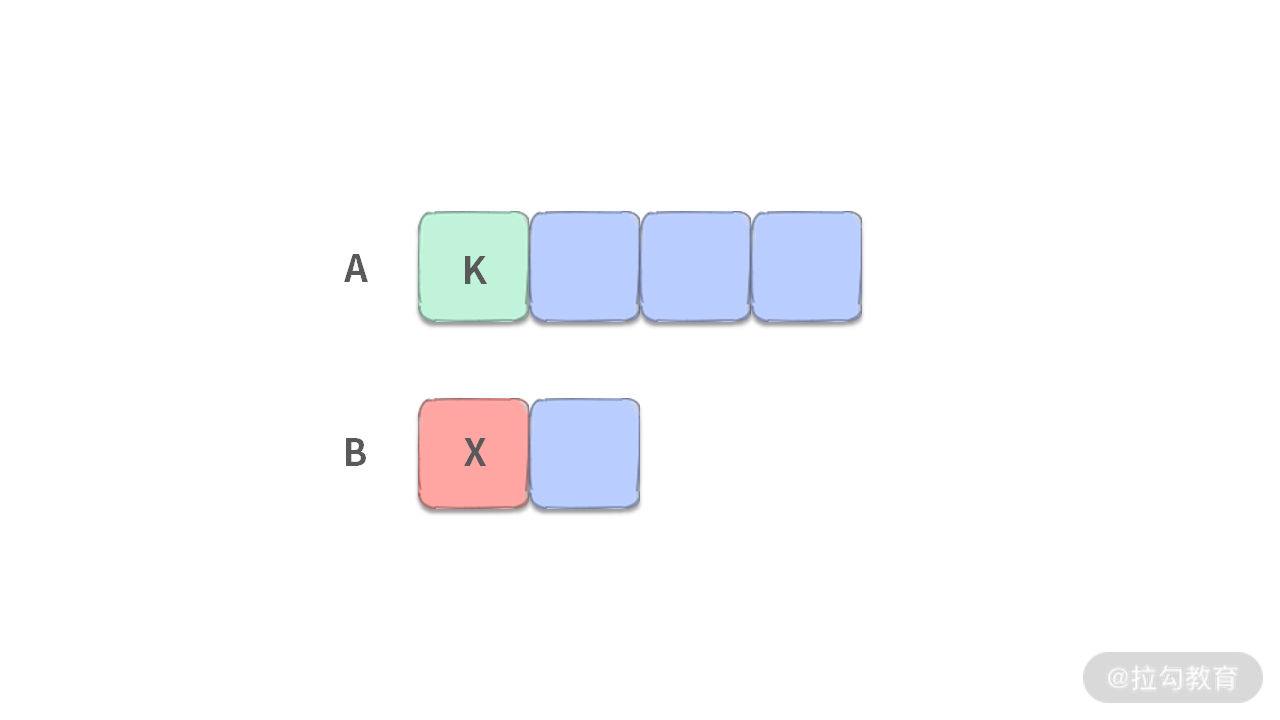
由于我们的目标是扔掉 4 个数,扔掉 2 个数之后,还需要再扔 2 个数。此时我们只需要比较数组开头的一个元素 K, X 的大小,谁小就把谁扔掉。这里我们假设 K 比较小。
- 第 3 步:此时还剩下 1 个数需要扔掉,那么只需要扔掉 M 和 X 中较小的就可以了。
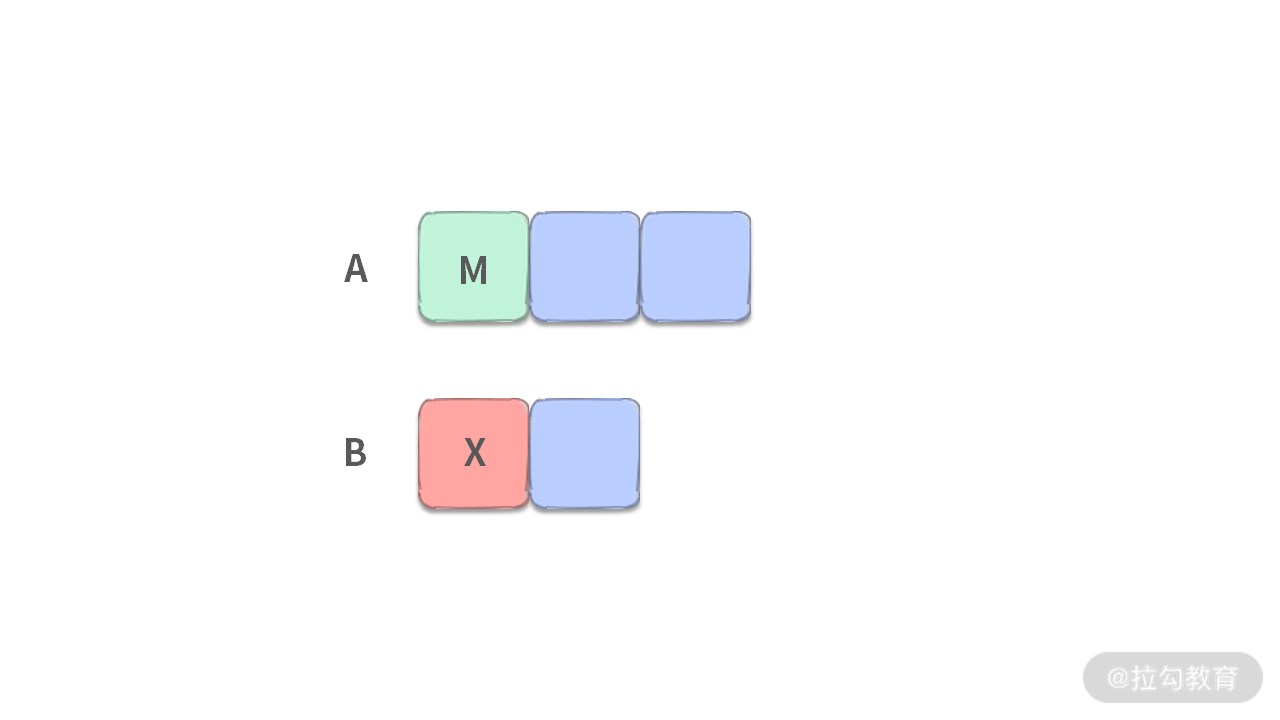
【结论】当我们需要扔掉 k 个元素:
- k 是偶数的时候,我们只需要比较 A[k/2-1] 和 B[k/2-1] 的大小,谁小就扔掉对应的 [0…k/2-1] 这一段;
- k 是奇数的时候,我们只需要比较 A[k/2] 和 B[k/2] 的大小,谁小就扔掉对应的 [0…k/2] 这一段。
如前面所展示的推导过程,无论 k 是偶数还是奇数,这两种情况都可以用反证法来证明。这里我总结一下偶数的情况:
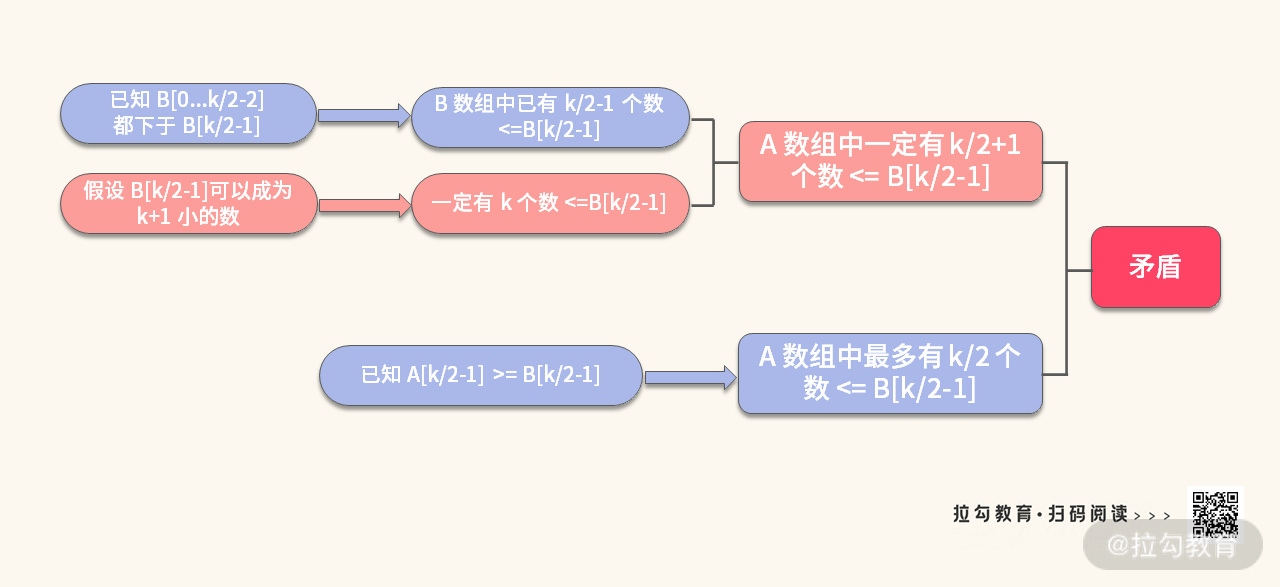
思考题:你能证明 k 为奇数的情况吗?
分析:不过由于整数在程序中的整除特性,我们可以将奇数和偶数的情况统一起来。需要扔掉 k 个数的时候,p = (k-1)/ 2,你只需要比较 A[p] 和 B[p] 的大小即可。如果 A[p] >= B[p],那么就可以把 B[0….p] 这段都扔掉。
【代码】根据之前的思考,我们可以得到如下解法(解析在注释里):
double findMedianSortedArrays(int[] A, int[] B) {final int len = A.length + B.length;final int alen = A.length, blen = B.length;int i = 0, j = 0;if (len == 0) {return 0;}int k = (len - 1) >> 1;while (k > 0) {final int p = (k - 1) >> 1;if (j + p >= blen || (i + p < alen && A[i + p] < B[j + p])) {i += p + 1;} else {j += p + 1;}k -= p + 1;}double front =(j >= blen || (i < alen && A[i] < B[j])) ? A[i++] : B[j++];if ((len & 1) == 1) {return front;}double back =(j >= blen || (i < alen && A[i] < B[j])) ? A[i] : B[j];return (front + back) / 2.0;}
复杂度分析:一共要合并的长度可以认为是 N/2,然后每次取一半进行合并。因此,合并次数为 O(lgN),空间复杂度为 O(1)。
【小结】至此,我们需要总结一下这道有点数学趣味的题目(实际上只是用了一个简单的反证法)。
如果,我们再看一下合并排序的过程(这里我加了一个变量 k):
int alen = A.length;int blen = B.length;int k = alen + blen, to = 0;int[] t = new int[k];while (k > 0) {if (j >= blen || i < alen && A[i] <= B[j]) {t[to++] = A[i];i += 1;} else {t[to++] = B[j];j += 1;}k -= 1;}
再看这道题的核心循环的写法:
int alen = A.length, blen = B.length;int len = alen + blen;int k = (len - 1) >> 1;int i = 0, j = 0;while (k > 0) {final int p = (k - 1) >> 1;if (j + p >= blen || (i + p < alen && A[i + p] < B[j + p])) {i += p + 1;} else {j += p + 1;}k -= p + 1;}
我们发现,正常情况下的合并排序,就是步长 p = 0 的时候的特例。那么接下来我们归纳一下合并的用法:

那么合并模板还有没有别的用法呢?这里我给你留了两道练习题。
练习题 1:给定两个有序数组 A,B。假设 A 数组中有足够的空间,不借助外部存储空间的情况下,请将 A,B,两个数组合并至 A 数组中。
练习题 2:合并两个有序链表
如果你做完练习,应该就可以将合并模板的知识图谱补充如下了:
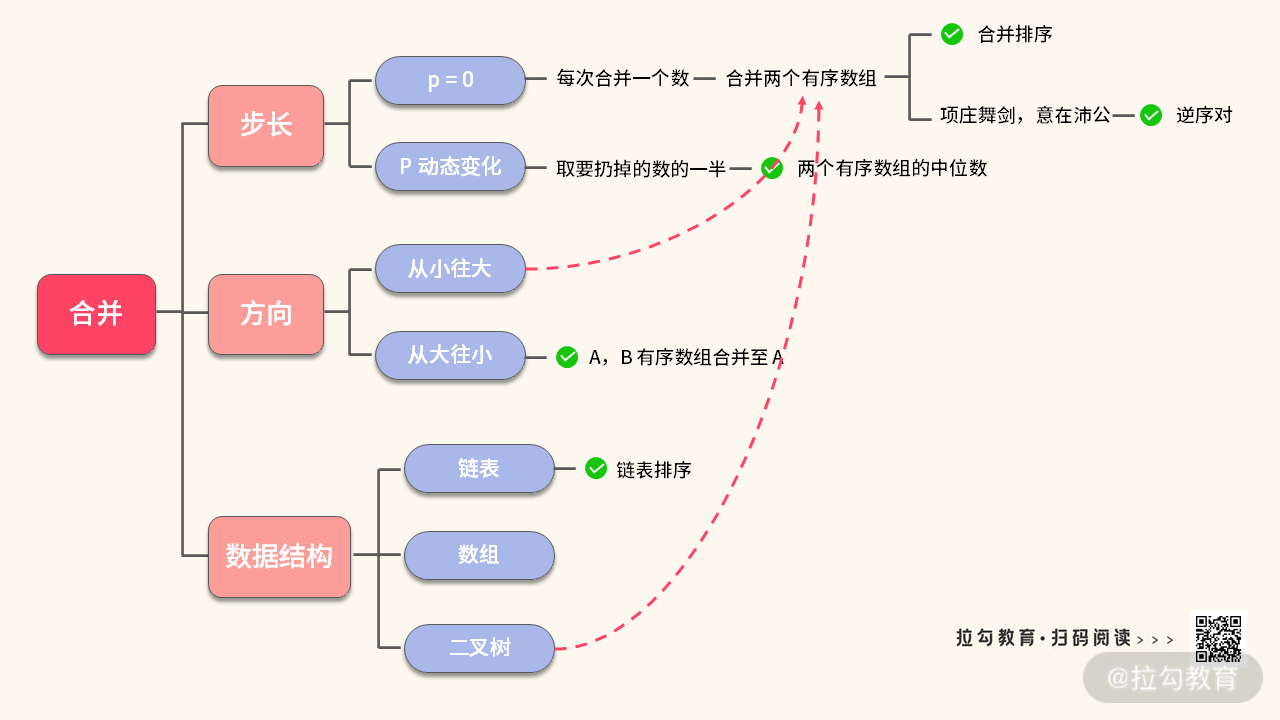
一个小小的合并模板可就以解决这么多问题,多积累模版可以帮助我们在面试中快速答题,希望你理解并且背下来这个模板!你自己还整理过其他的通用性较强的模板吗?可以在留言区和我分享。
快速排序
快速排序也是我们在算法书里面认识的老朋友了。不过今天我仍然不会按照书里面的套路来介绍快速排序。前面我介绍了合并排序与二叉树的后序遍历有非常类似的地方,那么快速排序又和什么遍历相似呢?
是二叉树的前序遍历!前序遍历有两个重要的特点:
- 拿到根结点的信息
- 将根结点的信息,传递给左右子树
对于排序来说,有序性就是信息。因此,我们要做的事情就是把能拿到的有序信息,传递给左子数组和右子数组。
1. 有序性的传递
对于快排而言,它传递有序性的手段就是将选择一个数 x,并且利用这个数,将数组分成三部分:
- 小于 x 的部分放在数组的最前面
- 等于 x 的部分放在数组的中间
- 大于 x 的部分放在数组的最后面
2. 左右子数组的处理
此时,可以把小于 x 的部分当成二叉树中的左子树,大于 x 的部分当成二叉树的右子树。等于 x 的部分当成二叉树的根结点。
那么接下来要做的事情就是像前序遍历一样,递归地处理左子数组和右子数组。
这里我们模拟一下像前序遍历一样的快速排序,演示如下动图所示:
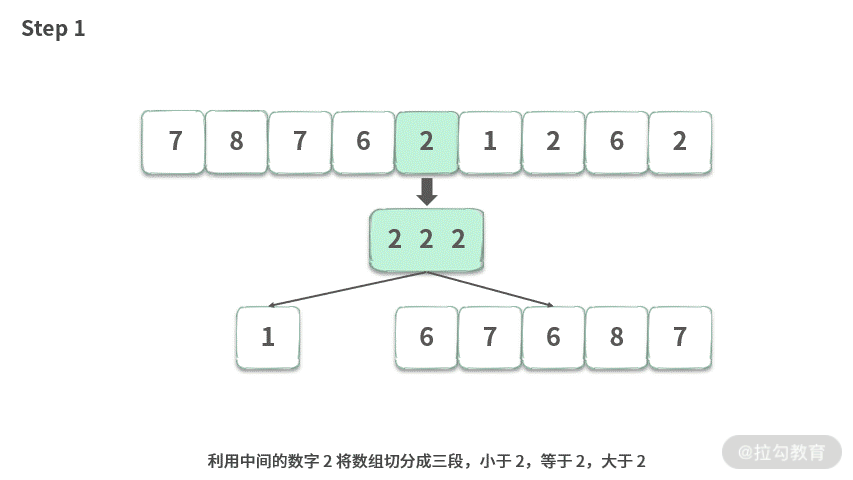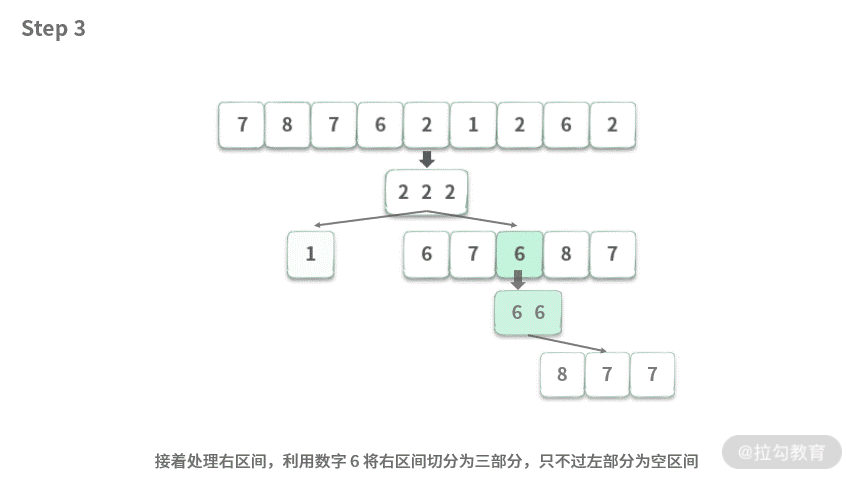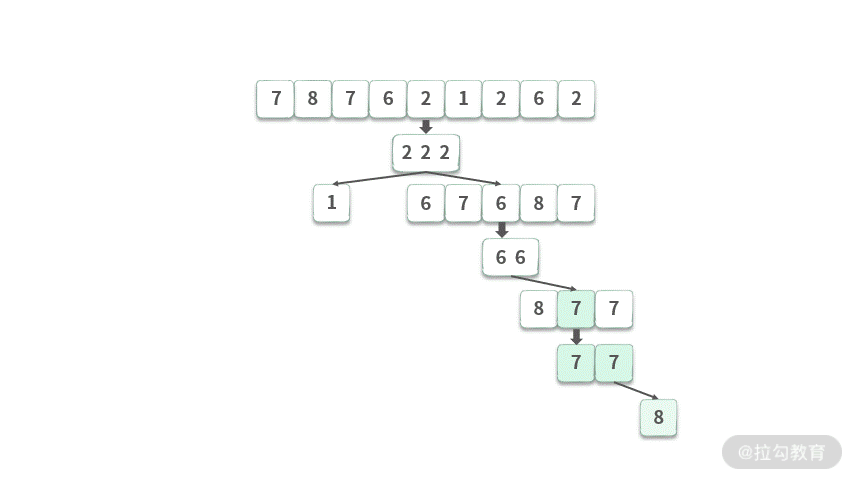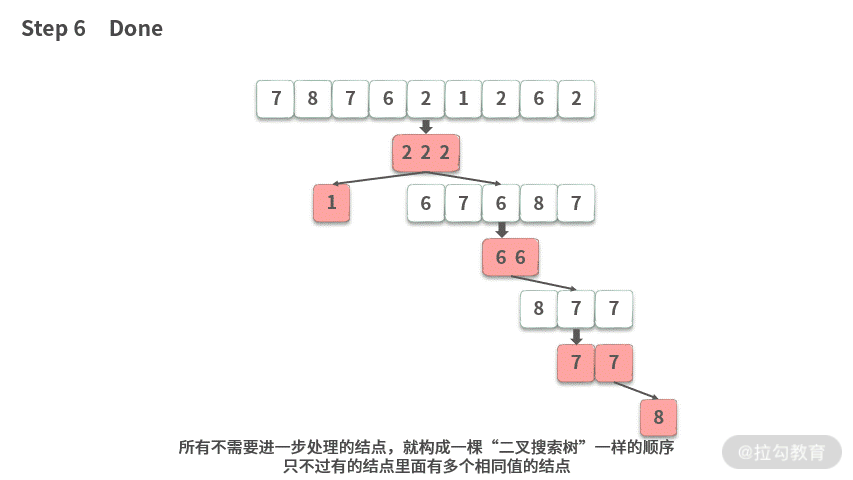
相对于二叉树的前序遍历来说,快速排序也有它自己的特点:
- 根结点的处理,需要执行 “三路切分” 操作,将一个数组切分为三段;
- 左右子区间是由切分动态生成的,并不像二叉树那样由指针固定。
可以用伪代码表示如下:
function 前序遍历/快速排序():获取根结点的信息将根结点的信息传递左右子树/左右子数组
那么前序遍历 / 快速排序的考点就可以总结为以下 3 点:
- 如何划分子结构
- 获取根结点的信息
- 如何将根结点的信息,传递给左右子树 / 左右子数组。
我们可以把前序遍历与快速排序关联信息表达如下:
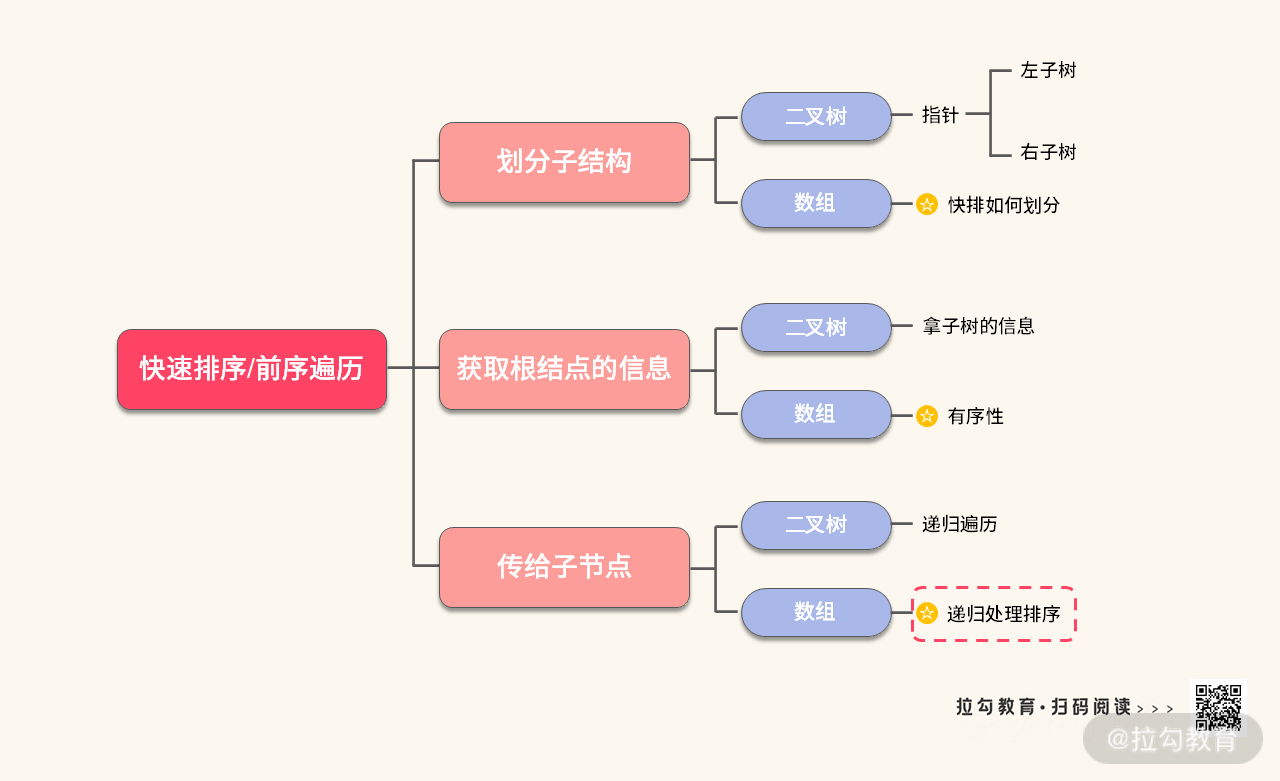
那么接下来我们就从上图中展示的三个方面入手,并且与二叉树的前序遍历的代码对照着一起看。
1. 划分
首先我们看一下如何划分子数组。对于二叉树而言,子树的划分是天然的,已经在数据结构里面约定好了,比如 TreeNode.left、TreeNode.right。
但是对于数组而言,切分的时候,如果想到达最优的效率,那么将数组切为平均的两半效率应该是最高的(可以联想到二叉平衡树的效率)。但是快排不能保证选择一个数,就一定能将数组切分成为两半。
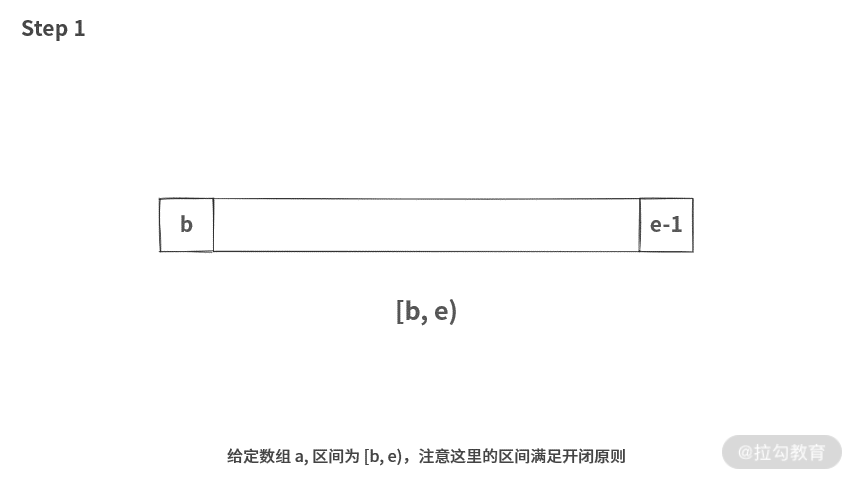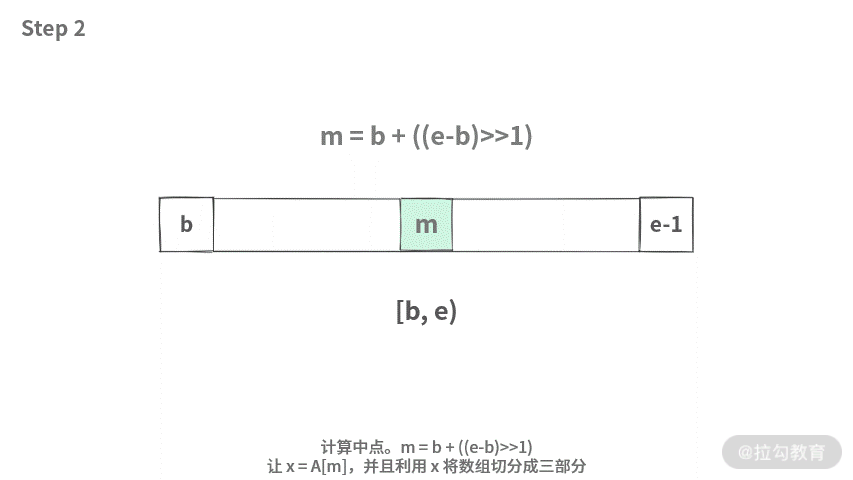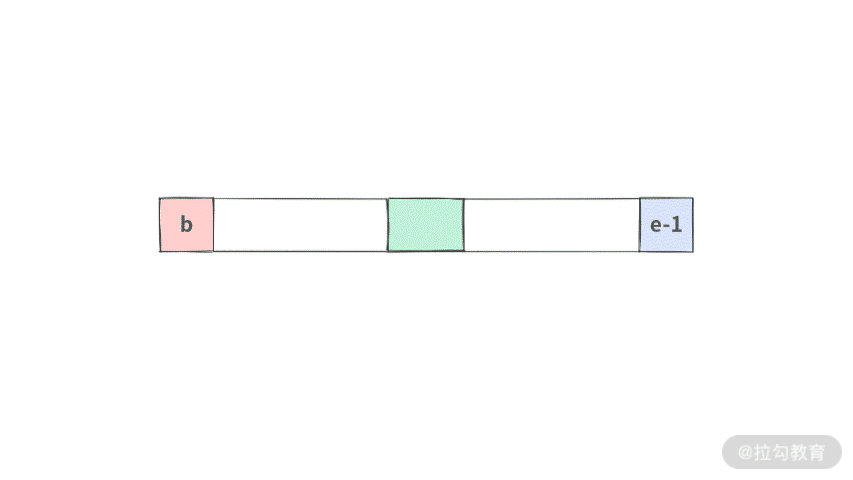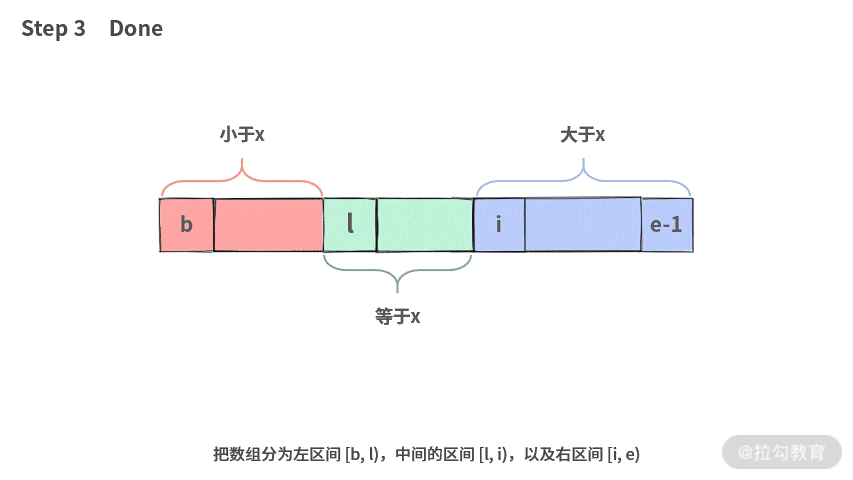
切分的结果如下:
利用x将数组 A[]切分为三段,[小于x的部分,等于x的部分,大于x的部分]左子树 = [小于x的部分] = [b, l)根结点 = [等于x的部分] = [l, i)右 子树 = [大 于x的部分] = [i, e)
2. 子数组的递归
由于这里是排序,就需要分别对左子数组和右子数组进行排序。如果你还能想起来我们之前介绍过的 “二叉树的前序遍历”,那么对子数组的排序应该也只需要递归就可以了。
preOrder(root.left);preOrder(root.right);
快速排序则需要这么写:
qsort(a, b, l);qsort(a, i, e);
最后,我们还需要考虑一下边界情况:
- 当 b >= e 的时候,说明这个区间是一个空区间,没有必要再排序;
- 当 b + 1 == e 的时候,说明只有一个元素,也没有必要排序。
以上两种边界情况可以对应到当二叉树为空,以及二叉树只有一个结点的情况。
【代码】让我们一起写一下快速排序的代码吧(解析在注释里):
void swap(int[] A, int i, int j) {int t = A[i];A[i] = A[j];A[j] = t;}void qsort(int[] A, int b, int e) {if (b >= e || b + 1 >= e) {return;}final int m = b + ((e - b) >> 1);final int x = A[m];int l = b, i = b, r = e - 1;while (i <= r) {if (A[i] < x) {swap(A, l++, i++);} else if (A[i] == x) {i++;} else {swap(A, r--, i);}}qsort(A, b, l);qsort(A, i, e);}void quickSort(int[] nums) {if (nums == null)return;qsort(nums, 0, nums.length);}
复杂度分析:快速排序在较优情况下是 O(NlgN),在较差情况下是 O(N2)。
不过,我们好像还没有详细地介绍怎么进行切分操作,也就是如何将数组切分成三部分。由于切分非常重要(在 EMC 的面试中曾经单独出现过),所以我们重点介绍一下,暂且把它叫作 “三路切分”。
例 3:三路切分
【题目】给定一个只包含 [0, 1, 2] 的数组,如何只通过 swap 操作,将这个数组进行排序?
输入:[2, 1, 0]
输出:[0, 1, 2]
要求:你的时间复杂度需要是 O(N),空间复杂度需要是 O(1)。
【分析】回想一下,我们前面学过的 “三路切分”,在快速排序的时候,我们通过一个整数 x 将数组切分成小于、等于、大于三部分。分别可以映射到三个值上:
- 0 的部分对应到小于 x 的部分
- 1 的部分对应到等于 x 的部分
- 2 的部分对应到大于 x 的部分
问题的关键就是如何在时间复杂度 O(N),空间复杂度 O(1) 条件下完成这个操作。我们假设数组已经被切分成 4 段,如下图所示:
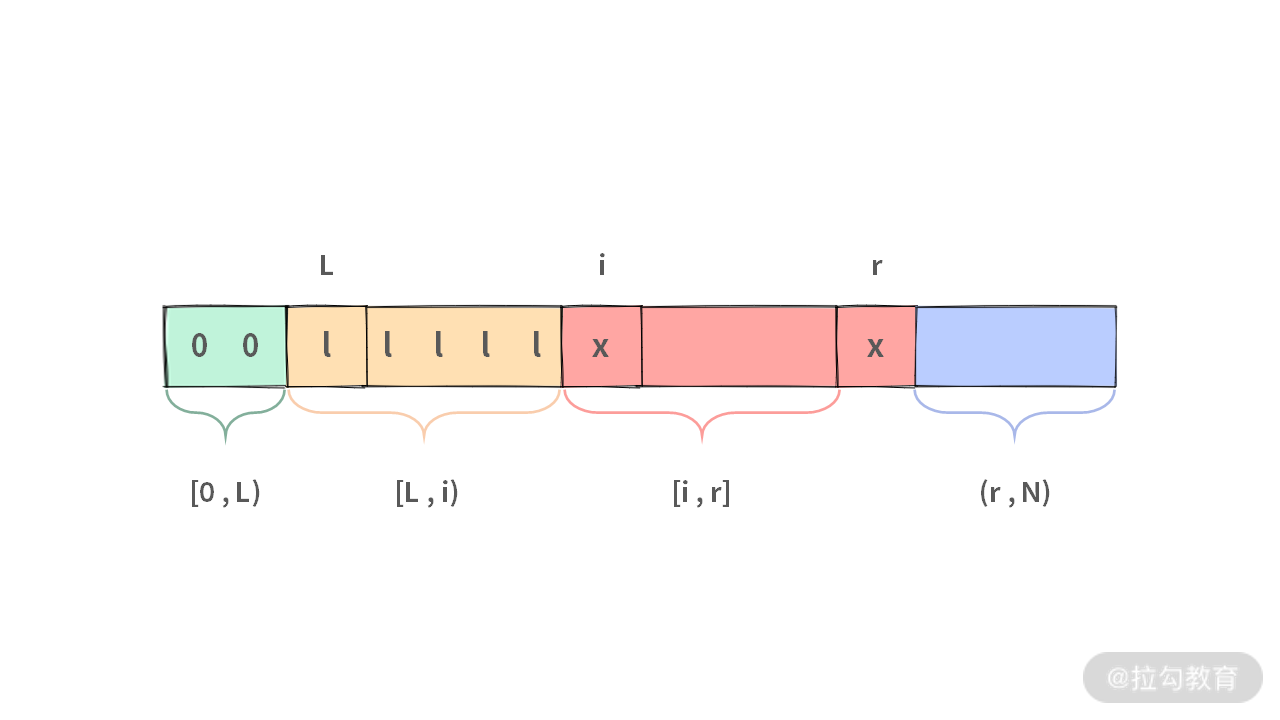
对于这 4 段区间,我们需要有以下约束(注意这里都要满足开闭原则):
- [0, L) 表示全是 0 的区间
- [L, i) 表示全是 1 的区间
- [i, r] 表示还是未处理的数的区间
- (r, N) 表示全是 2 的区间
后续所有的操作都必须满足这个性质。
初始条件:L = 0, i = 0, r = N - 1。形成的 4 个区间就是:[0, 0), [0, 0), [0, N-1], (N-1, N),除了 [0, N-1] 非空以外,另外 3 个区间都是空集,所以满足前面对区间的约束原则。
推导:在 [i, r) 区间中的值 x 取值只可能是下面 3 种情况(x = 0, x = 1, x = 2),我们分别处理如下。
- 当 x = 0 的时候,我们想要把 0 放到 [0, L) 区间里面,也就是插入到所有的 1 的前面。
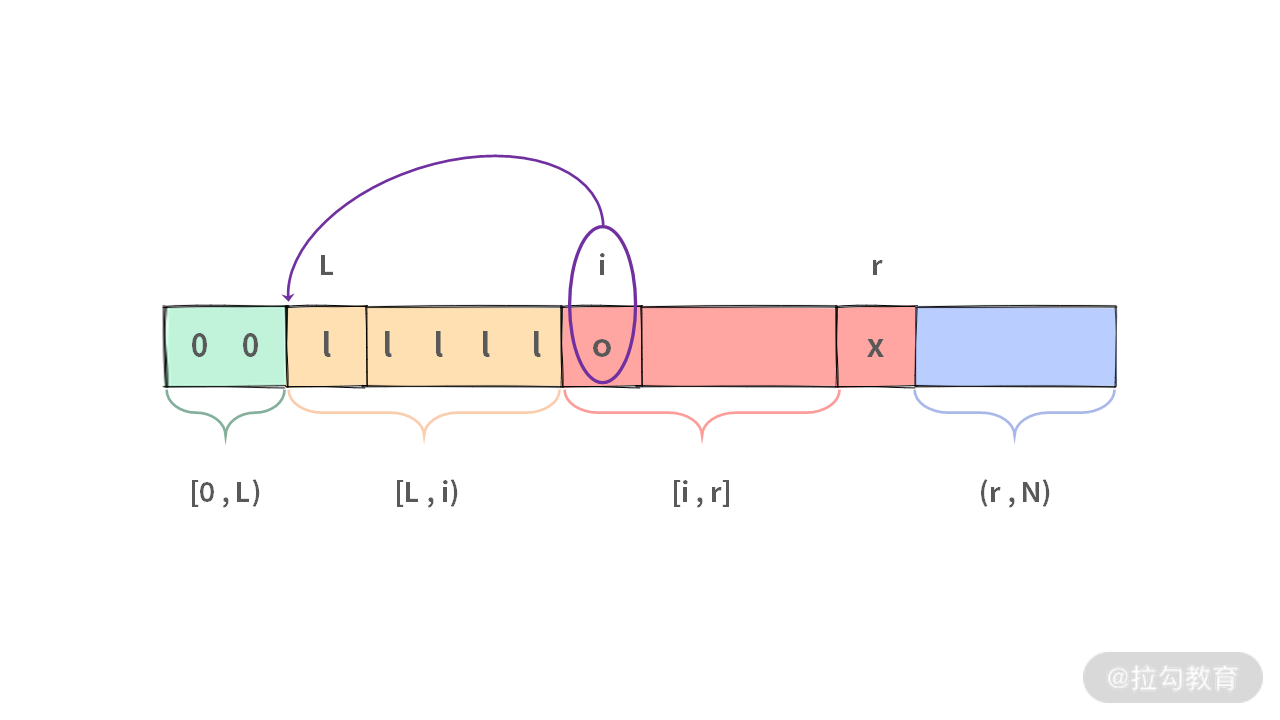
除了像插入排序一样一个一个地移动 1,还有没有更好的办法呢?
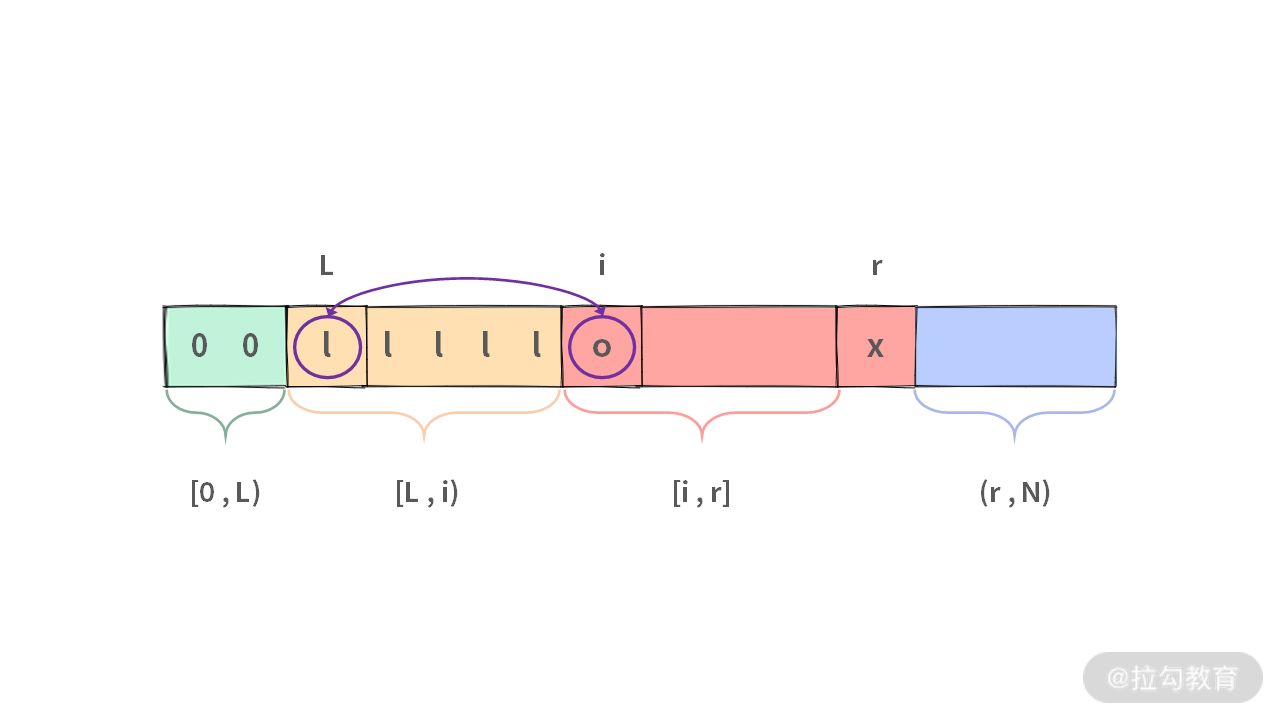
答案是,不需要一个一个移动!因为 [L, i) 区间里面全都是 1,只需要将 A[L] 与 A[i] 进行交换即可。
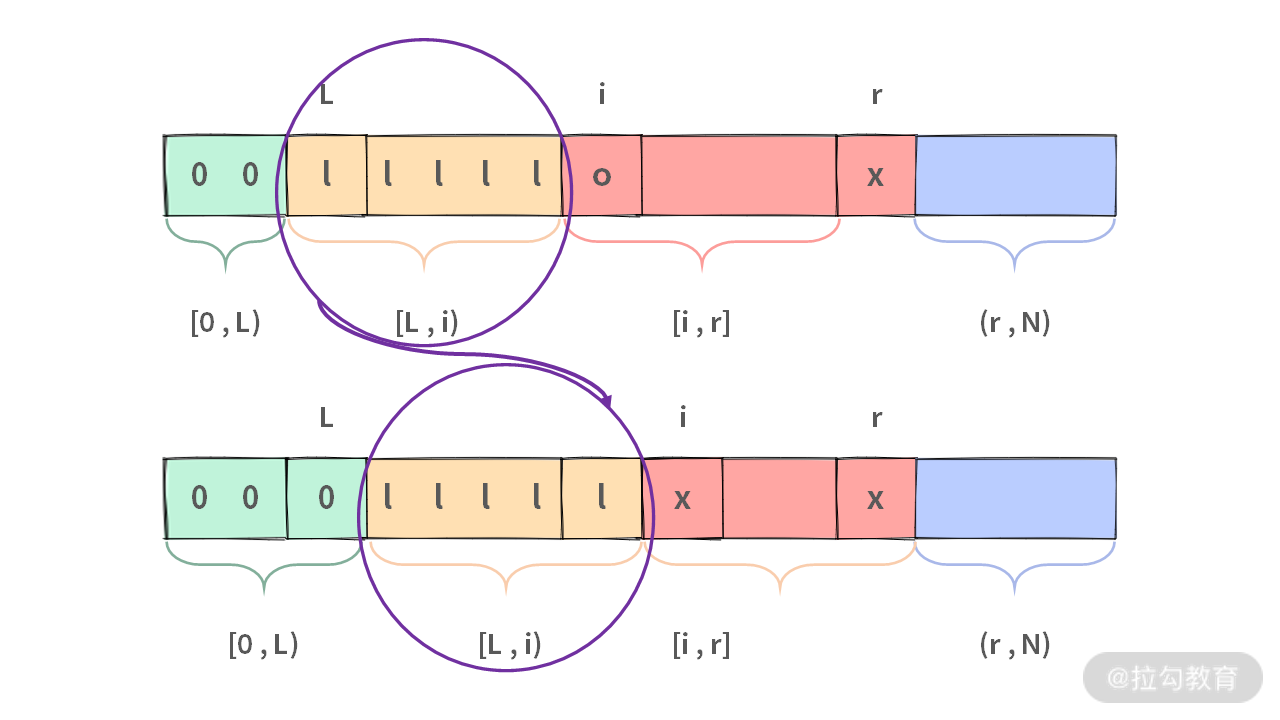
不过由于 A[L] 与 A[i] 交换完成之后,看起来像是一个新来的 0 插入到区间 [L, i) 的前面,[L, i) 区间整体向右平移了一样。所以需要执行 L++, i++。经此操作,变更后的区间仍然满足约束。
- 当 x = 1 的时候,就比较简单了。只需要为 1 的区间 [L, i) 向右扩展一下就可以了。
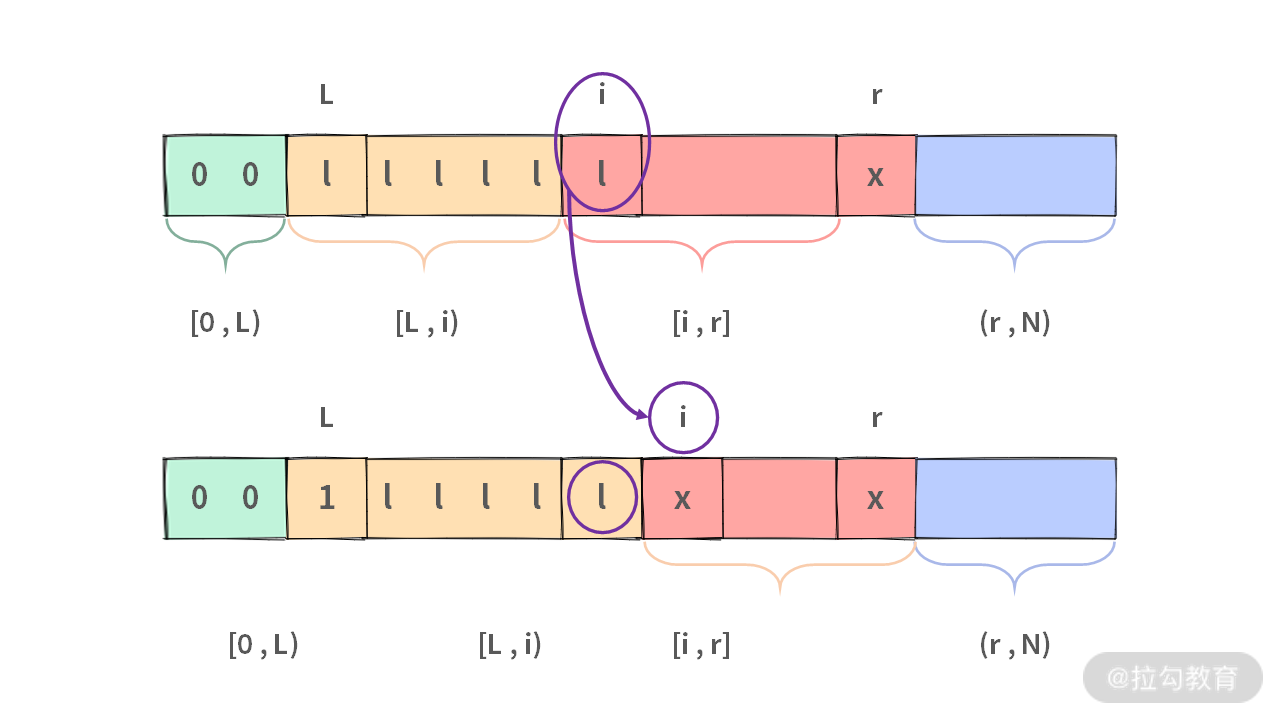
由于像 [L, i) 尾部增加了一个元素一样,所以只需要执行 i++ 就可以。区间变更后,仍然满足约束。
- 当 x = 2 的时候。首先需要执行 swap(A[i], A[r])。
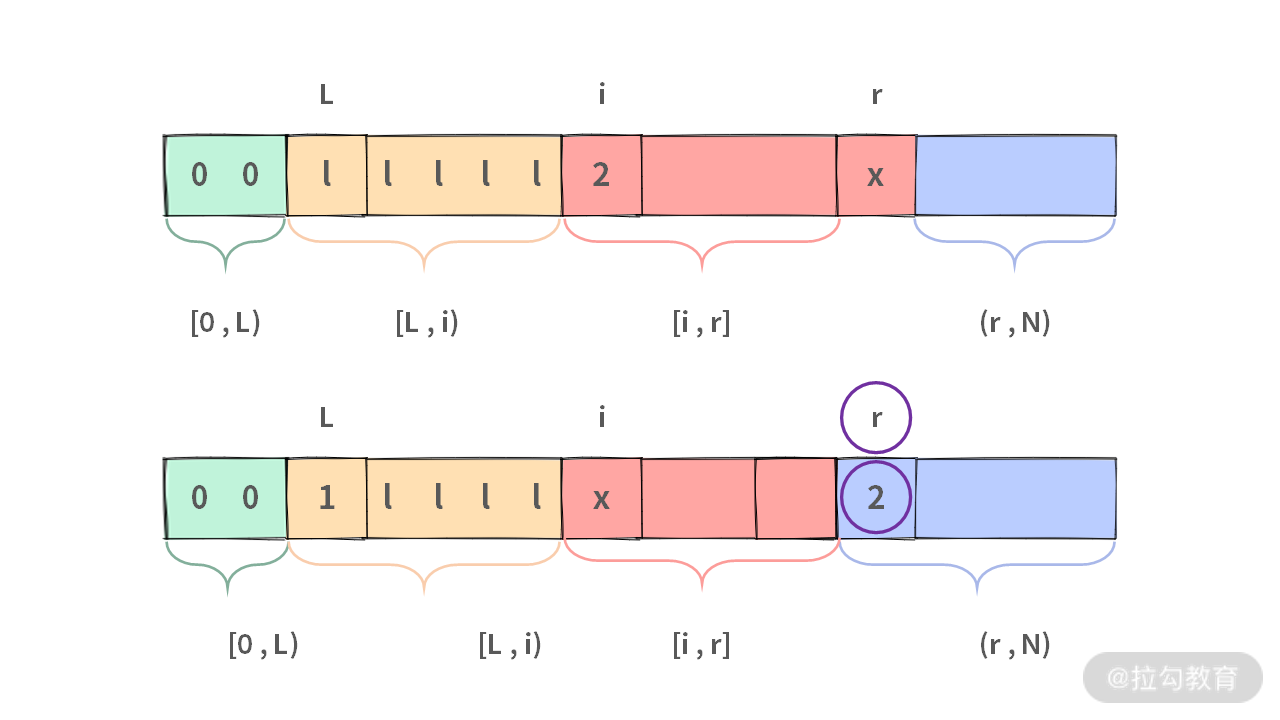
但是,如此一来,(r, N) 应该把左边新来的 2 包含进去,所以还需要在这个基础上执行 r—。区间变更后,仍然满足约束。
最终状态:所有的数都被处理之后,[i, r] 区间肯定为空集。由于两边都是取闭,那么必然当 i > r 的时候,[i, r] 才是空集。原本的四个区间,变成三个区间。
- [0, L) 等于 0 的区间
- [L, i) 等于 1 的区间
- [i, N) 等于 2 的区间。注意此时由于 i > r,实际上 i = r + 1,那么区间 (r, N) 就是 [i, N)。
由于最终状态是将一个乱序的数组切分成三部分,所以这个方法又叫三路切分。
【代码】到此为止,相信你已经可以根据思路写出代码了(解析在注释里):
void swap(int[] A, int i, int j) {int t = A[i];A[i] = A[j];A[j] = t;}void split(int[] A) {final int N = A.length;int i = 0, l = 0, r = N - 1;while (i <= r) {if (A[i] == 0)swap(A, l++, i++);else if (A[i] == 1)i++;elseswap(A, r--, i);}}
复杂度分析:时间复杂度是 O(N),空间复杂度是 O(1)。因此满足题目要求。
【小结】这道题目如果没有只能用 swap 操作这个限制还是很简单的,但加上这个限制之后。你就只能使用 “三路切分” 的绝技了。三路切分的考点可以总结如下:
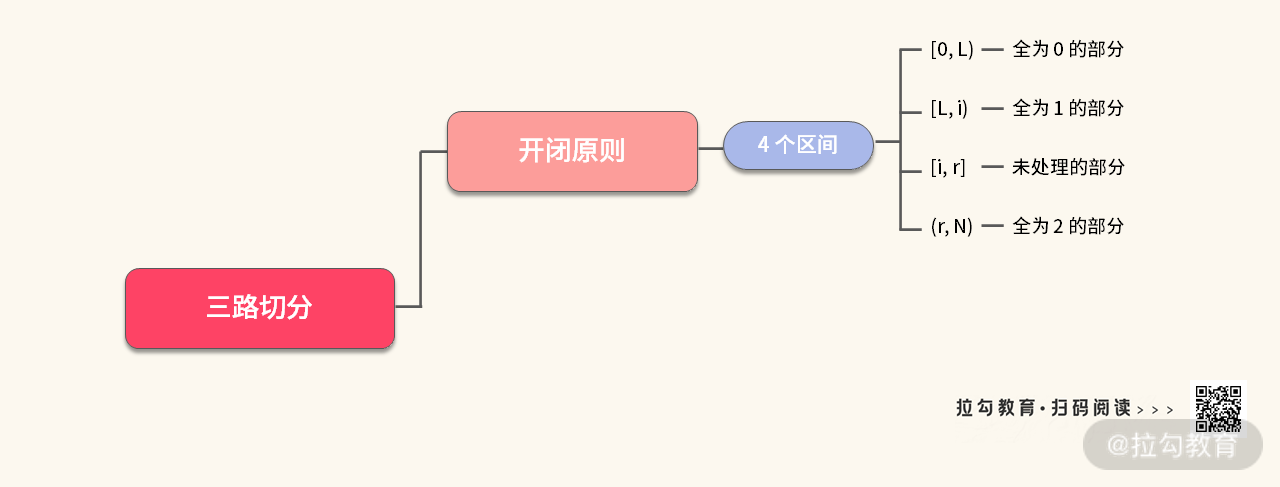
由上图可以知,三路切分的考点比较单一。 这里我还给你留了一道练习题,帮你巩固下这个知识点。
练习题 3:数组中有 0 和非 0 元素,请把 0 元素移动到数组末尾。其他元素保持相对顺序不变。
三路切分不仅可以用在快速排序中,还有其他一些非常有趣的应用,让我们一起来看一下。
例 4:只出现一次的数
【题目】给定一个数组,除一个数以外,其他的数都出现了两次,请把这个数找出来。
输入:nums = [3,3,1,2,2]
输出:1
要求:时间复杂度 O(N)
【分析】对于这道题,这里我们不采用异或的做法,而是利用三路切分的方式来求解这道题,思路如下:
首先任意选择一个数 x,将数组进行 “三路切分”,得到的情况可能有以下 3 种(因为其他的数都是出现了两次)。
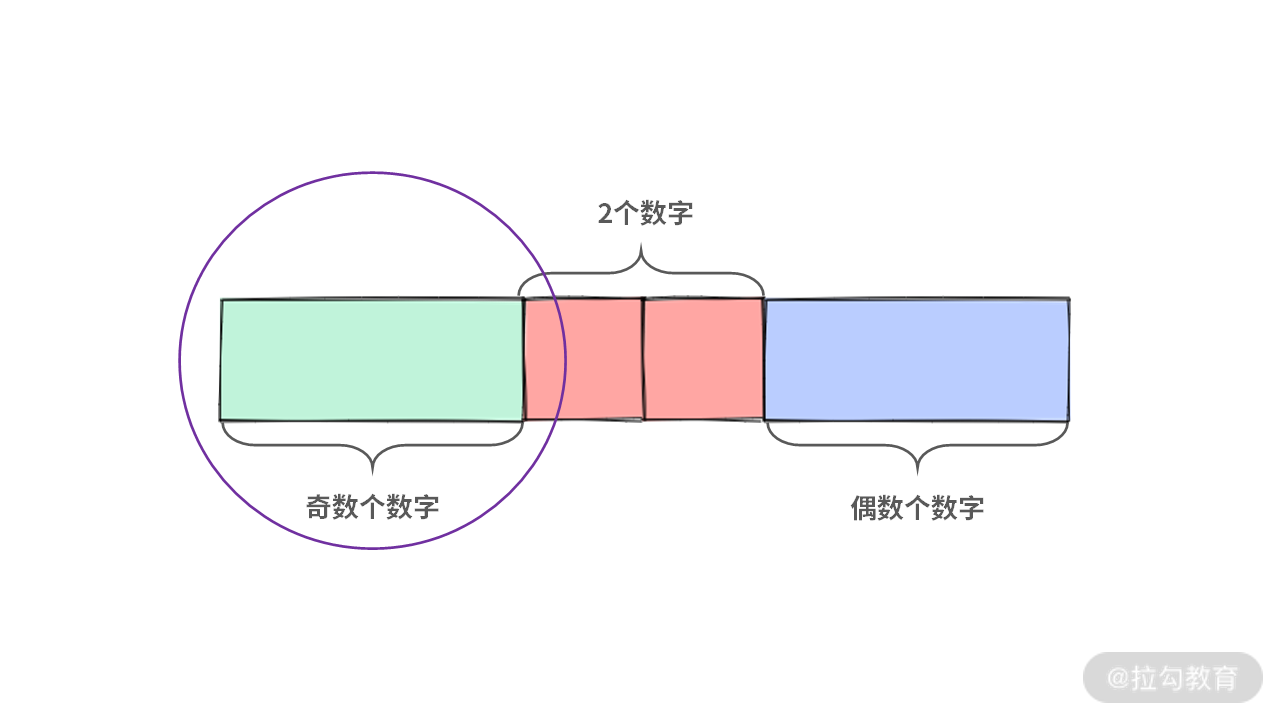
Case 1:只出现一次的数在左边,那么左区间的长度为奇数。
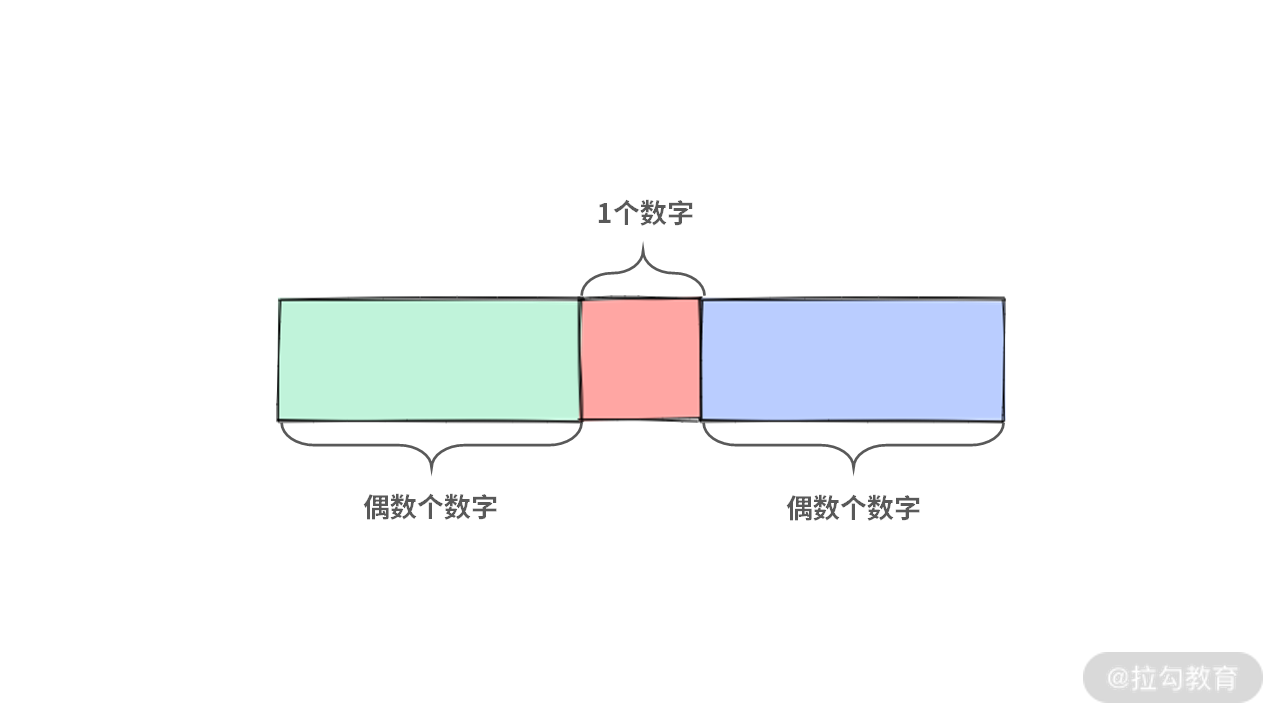
Case 2:只出现一次的数在中间,那么中间的数的长度为 1。直接返回 x。
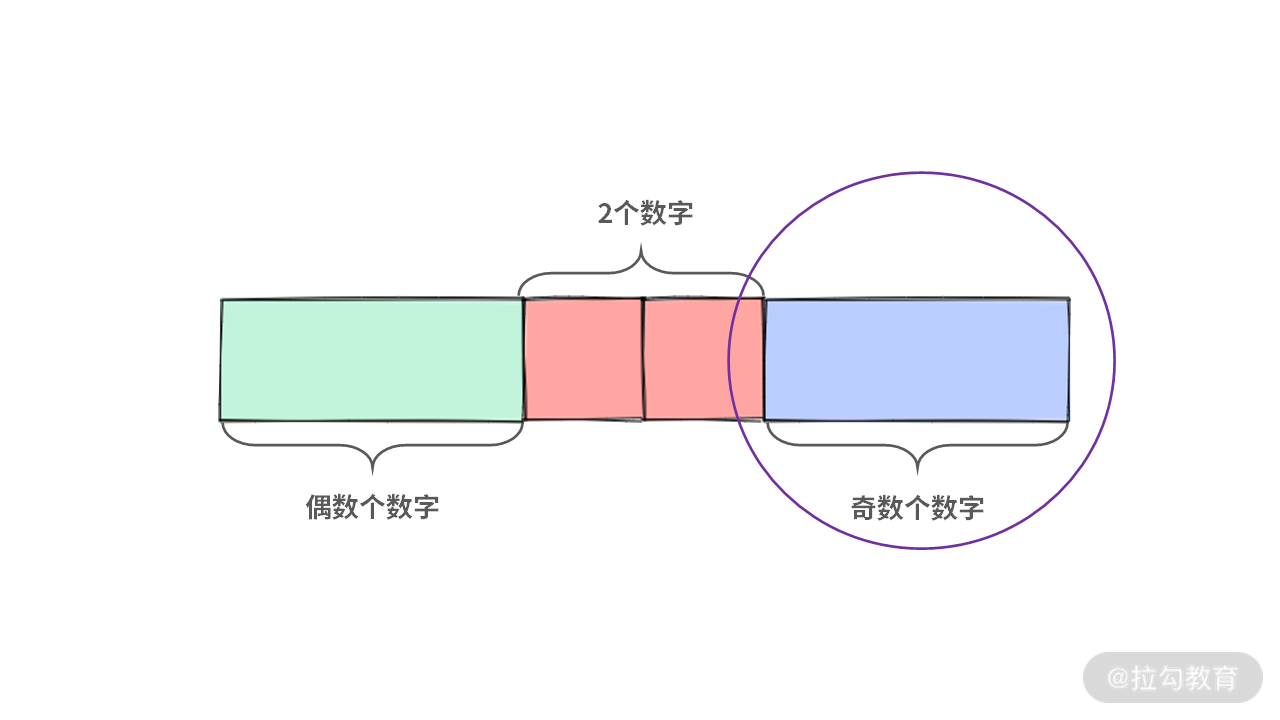
Case 3:只出现一次的数在右边,那么右区间的长度为奇数。
通过分析可知,前面 3 种情况中,只有 Case 2 得到了结果。接下来我们分别讨论 Case 1 和 Case3:在 Case 1 中,只出现 1 次的数在左区间时,只需要递归地处理左区间;在 Case 3 中,只出现 1 次的数在右区间时,只需要递归地处理右区间。
【代码】题目的思路还是相当简洁的,下面我们开始写代码吧(解析在注释里):
void swap(int[] A, int i, int j) {int t = A[i];A[i] = A[j];A[j] = t;}int threeSplit(int[] A, int b, int e) {if (b >= e) {return 0;}final int m = b + ((e - b) >> 1);final int x = A[m];int l = b;int i = b;int r = e - 1;while (i <= r) {if (A[i] < x) {swap(A, l++, i++);} else if (A[i] == x) {i++;} else {swap(A, r--, i);}}if (i - l == 1)return A[l];if (((l - b) & 0x01) == 1) {return threeSplit(A, b, l);}return threeSplit(A, i, e);}int singleNumber(int[] A) {if (A == null || A.length <= 0) {return 0;}return threeSplit(A, 0, A.length);}
复杂度分析:严格的时间复杂度计算是非常复杂的,《算法导论》中专门花了大量篇幅来分析。不过在本讲,我们可以简单地分析,每次扔掉的数组长度大概是 N/2,那么取极限累计求和,复杂度大概是 O(2N),也就是 O(N)。而变量只用了 O(1),如果栈也算上空间,那么大概是 O(H)。H 就是递归的深度。
【小结】尽管与位运算相比,这种解法算不上最优,不过也不失一种有趣的解法。下面我们再深挖一下这种解法的特点,与我们以前学过的知识联动一下。
这里我们与 “第 06 讲” 中介绍的 “二叉搜索树的查找”(练习题,你做了吗?)进行一下对比。二叉搜索树的查找代码可以写成如下(解析在注释里):
TreeNode searchBST(TreeNode root, int val) {if (root == null || root.val == val) {return root;}if (root.val > val) {return searchBST(root.left, val);}return searchBST(root.right, val);}
将上述代码与我们当前这道题的代码进行比较,会发现很多有趣的地方。
int threeSplit(int[] A, int b, int e) {if (b >= e) {return 0;}if (i - l == 1)return A[l];if (((l - b) & 0x01) == 1) {return threeSplit(A, b, l);}return threeSplit(A, i, e);}
为了方便你理解,我把这两部分代码的联系整理在下方的思维导图中,其中有非常有趣的联系:
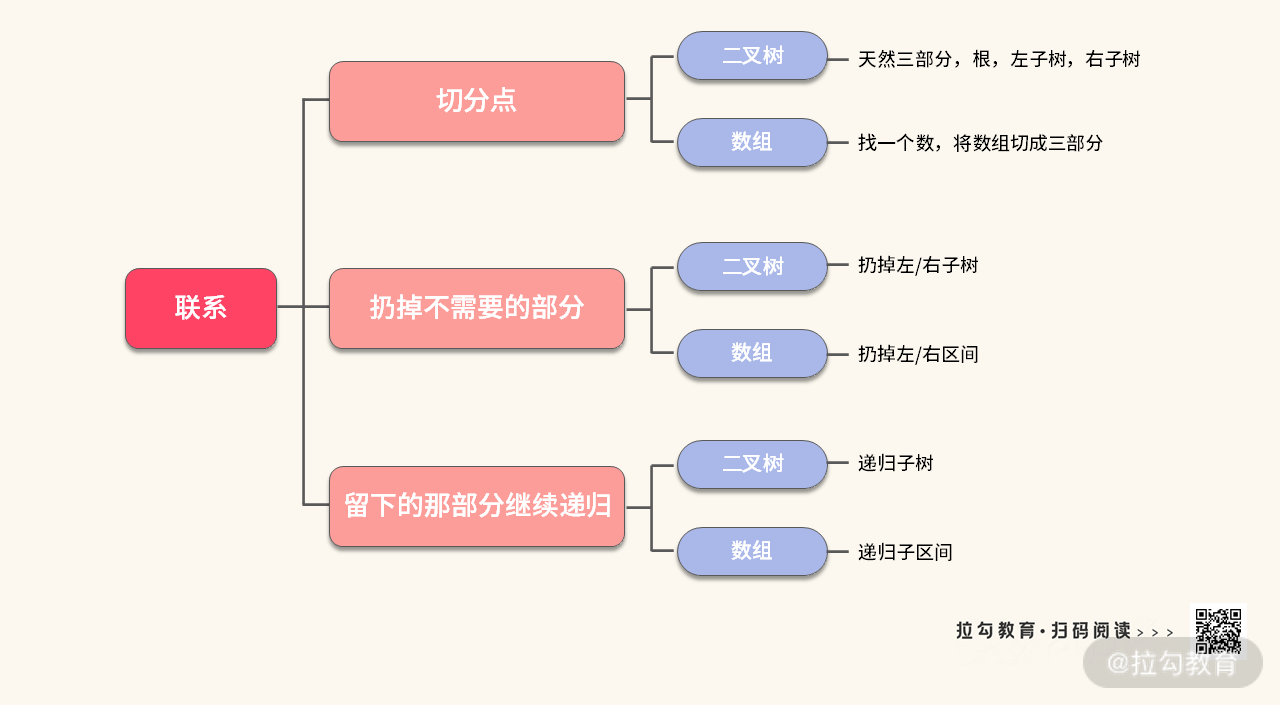
可以得出结论,数组其实是另外一种形式的二叉树,只不过有时候需要我们动态地把左 / 右子树给切分出来,不同的切分方式,可以解决不同的问题。
练习题 4:只出现一次的数,其他的数都出现了 3 次。请你把只出现一次的数找出来。
三路切分还有其他一些有趣的应用,让我们继续前进。
例 5:第 k 小的数
【题目】给定一个数组,请找出第 k 小的数(最小的数为第 1 小)。
输入:A = [2, 4, 1, 5, 3], k = 3
输出:3
【分析】如果我们把数组排序之后,直接取 A[k-1] 的数。那么就可以得到结果。但是有没有复杂度更低一点的算法呢?
仔细观察题目的特点:可以发现题目没有要求所有的数都有序,只是要求第 k 小的数即可。
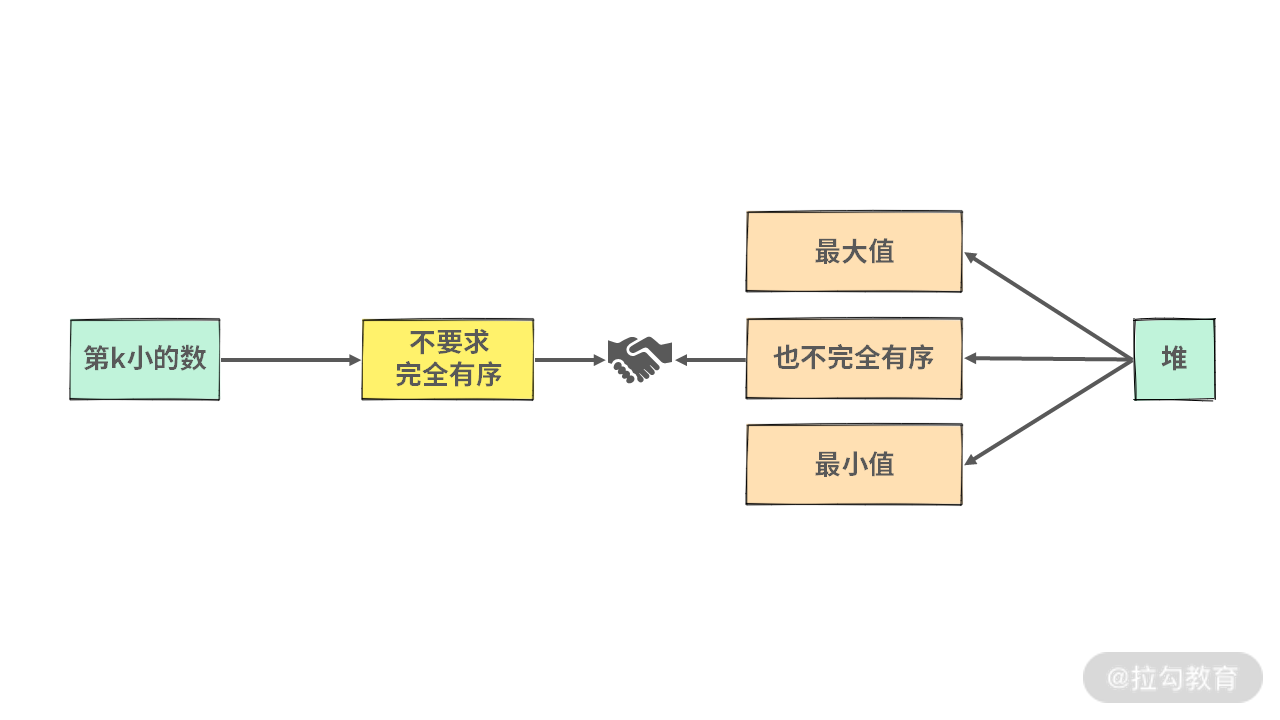
因此,这道题,应该可以用堆来解决。你能想一想吗?
我们再回顾一下前面的例 4 和例 5 两道题目。例 4 要求找出那个唯一的数。而例 5 中找到的第 k 小的数,也是唯一的。
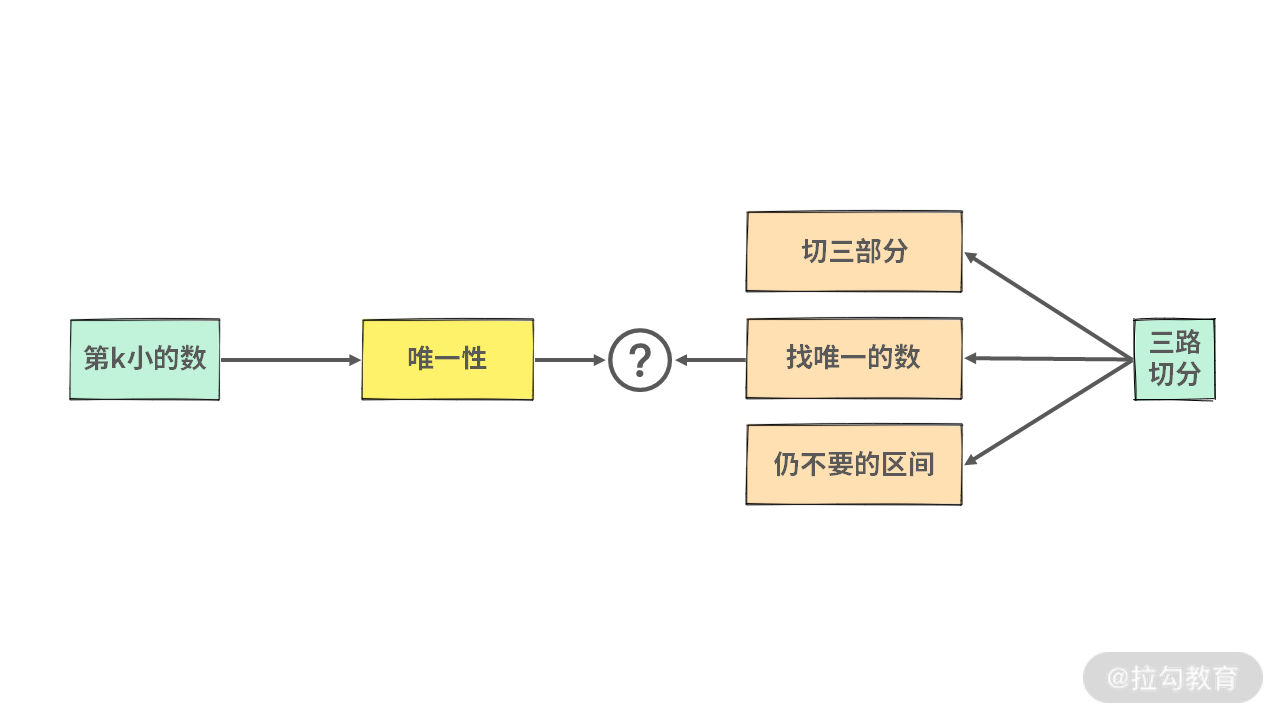
这里我们从题目的 “唯一性” 这个特点着手,可以发现:在例 4 中是需要判断这个唯一的数在哪个区间,那么就把其他的区间扔掉。如果能扔掉不要的区间,然后在余下的区间上递归,那我们就可以达到 O(N) 的时间复杂度了(和例 4 一样了)。
可是怎样才能判断第 k 小的数在哪个区间呢?三路切分完毕之后,应该有三个区间,下面我们基于这三个区间分别讨论。
注意:在写代码之前,我们还是要注意一下边界。由于题目中给定的 k 的值是从 1 开始。也就是当 k = 1 时,实际上对应的是最小的数,而我们数组的下标是从 0 开始的,先执行 k — 可以让 k 从 0 开始。(后面的 k 都是从 0 开始了!)
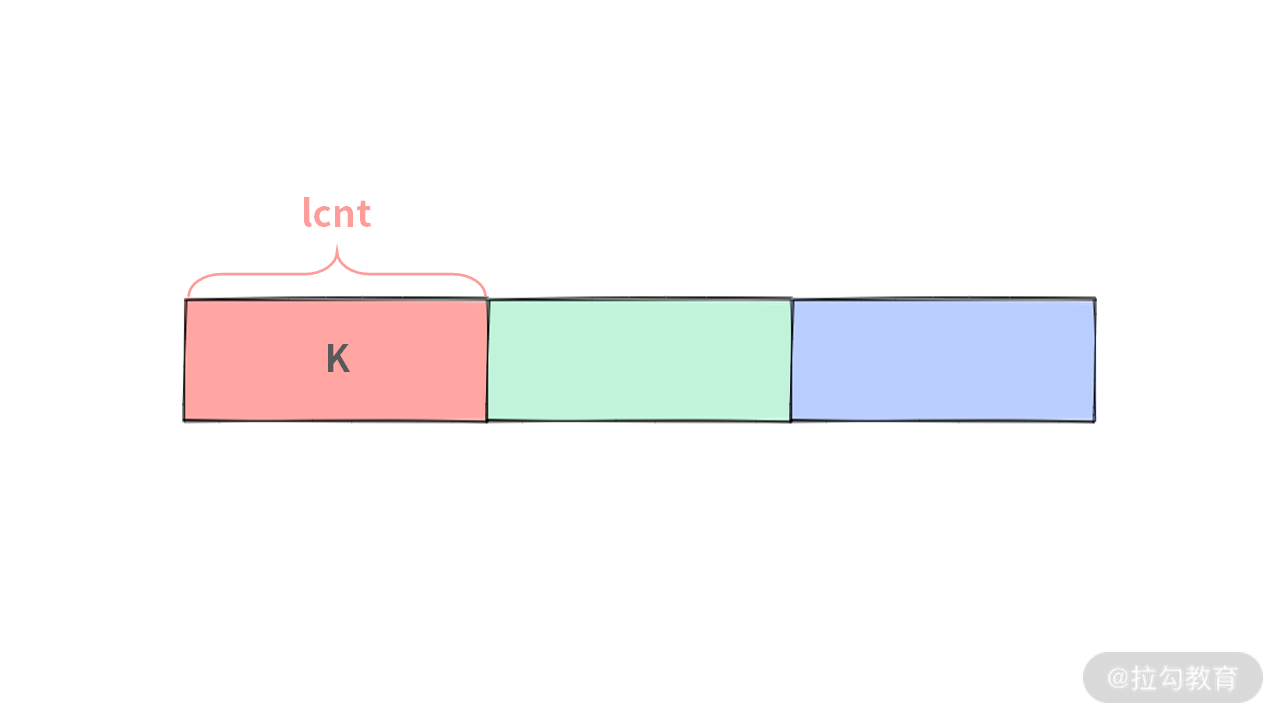
Case 1. 第 k 小的数在左区间,此时 k < lcnt,其中 lcnt 是左区间中数的个数。
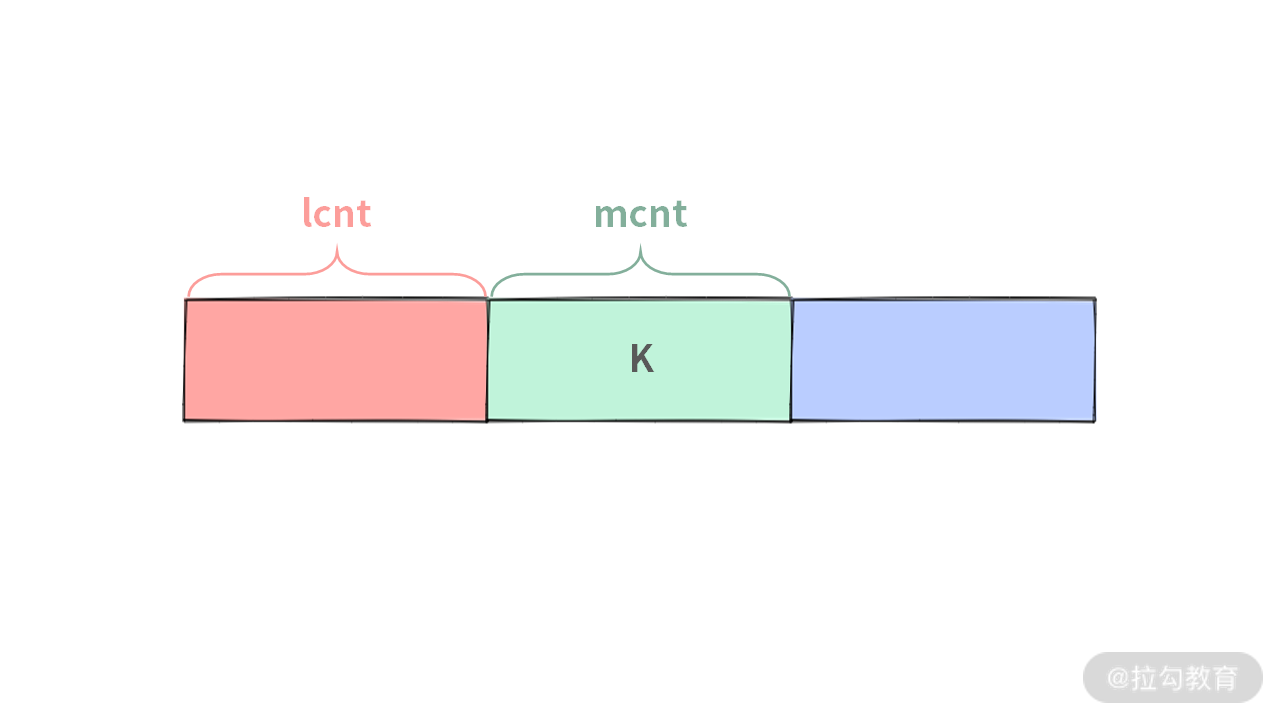
Case 2. 第 k 小的数在中间,此时 lcnt <= k < lcnt + mcnt。其中 mcnt 是中间区间的数的个数。
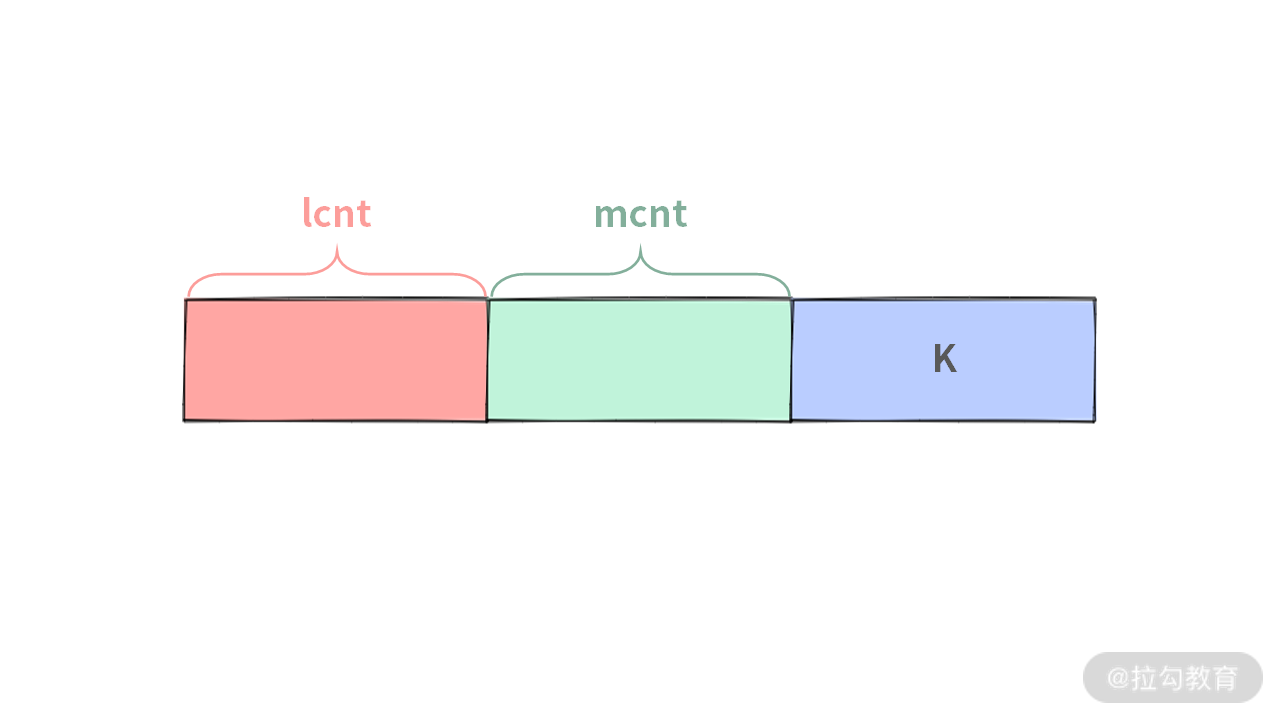
Case 3. 第 k 小的数在右区间,此时 k >= lcnt + mcnt。
那么,此时条件就会变成:
- k < lcnt 表示在左区间
- k >= lcnt && k < lcnt + mcnt 表示在中间
- k >= lcnt + mcnt 表示在右区间
【代码】有了前面的思路,那么我们一起来写一下这道题的代码(解析在注释里):
void swap(int[] A, int i, int j) {int t = A[i];A[i] = A[j];A[j] = t;}int kth(int[] A, int b, int e, int k) {if (b >= e) {return 0;}if (b + 1 >= e) {return A[b];}final int x = A[b + ((e - b) >> 1)];int i = b;int l = b;int r = e - 1;while (i <= r) {if (A[i] < x)swap(A, l++, i++);else if (A[i] == x)i++;elseswap(A, r--, i);}final int lcnt = l - b;final int mcnt = i - l;if (k < lcnt)return kth(A, b, l, k);if (k >= (lcnt + mcnt))return kth(A, i, e, k - lcnt - mcnt);return x;}int kthNumber(int[] A, int n, int k) {return kth(A, 0, n, k - 1);}
复杂度分析:时间复杂度 O(N),严格地分析非常复杂,你可以查看《算法导论》中推导,空间复杂度 O(H),H 是递归的深度。
【小结】如果我们将例 3 与例 5 放在一起,就可以总结出这些题的考点:
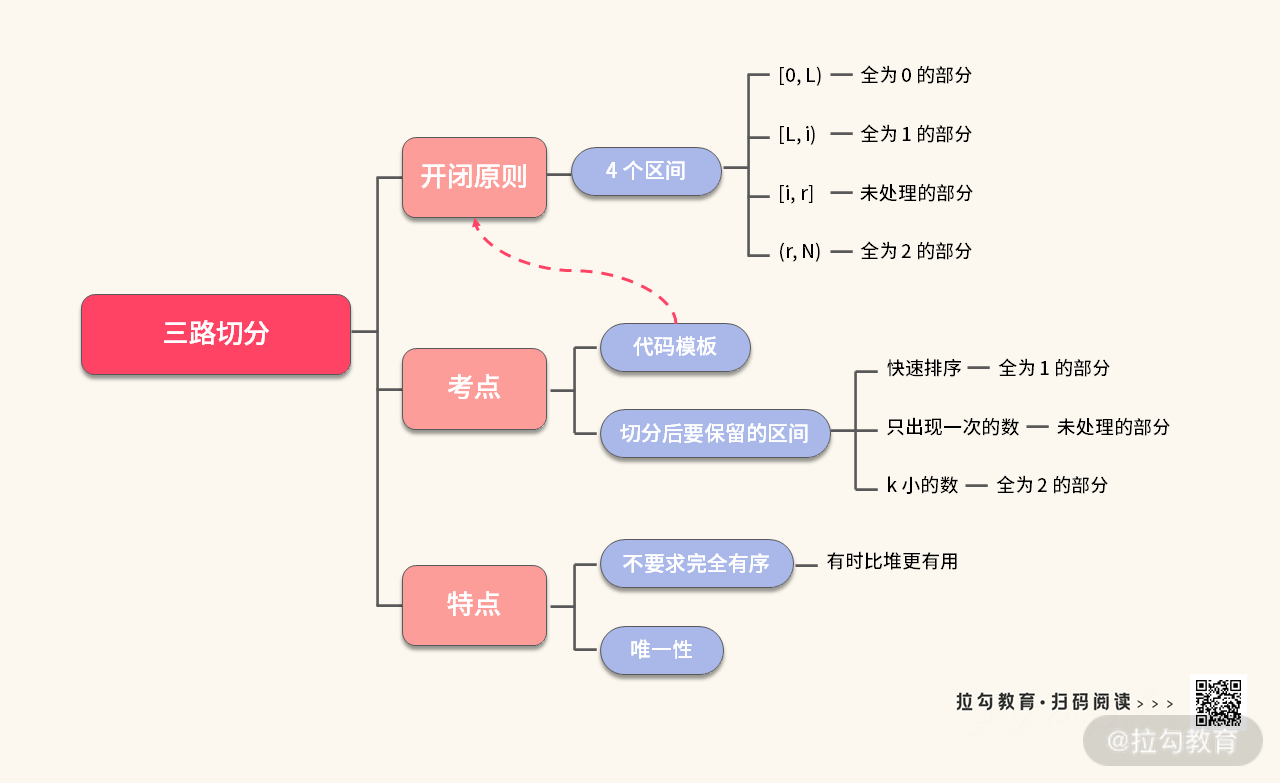
如果你已经掌握了例 5 里面的解题技巧与代码模板。那么接下来我们再进行一下深度扩展,你可以尝试思考下面这道练习题。
练习题 5:给定一个整数数组,请找出里面 k 个最小的数。
广度扩展:“三路切分” 本质上是将二叉树的一些思路移到数组上,那么是否可以适用到其他数据结构上呢?你可以在链表上试试,比如下面这道练习题。
练习题 6:排序一个单向链表(这里我们需要使用快速排序)
总结与延伸
在这里,我们一起学习了关于排序的两个知识点,合并排序和快速排序。我们再把介绍过的知识点进行一个汇总:
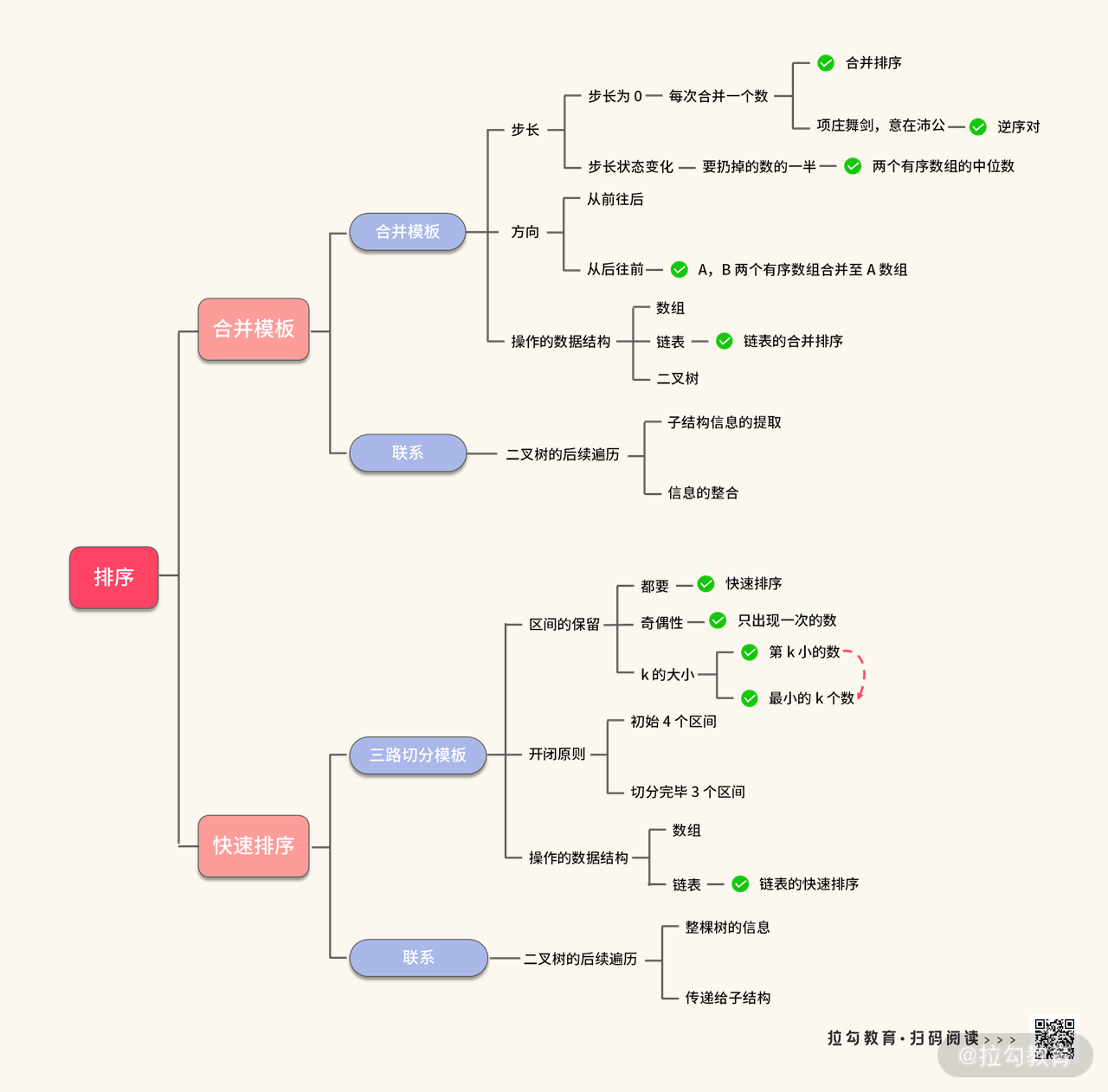
在本讲,虽然只讲了两个排序,但经过不断地浇灌,我们的知识树从萌芽逐渐长成了一棵大树。前面我们也提到过,实际上,堆在上浮或者上沉的时候,操作会与 “插入排序” 非常类似。由于篇幅的限制,这里我们不再去详细地挖掘插入排序了。
你可以自己思考和尝试,期待你还能发现更多排序的特点和巧妙用法,并且将它们总结下来,让你 “大树”(思维导图)像花儿一样开得绚烂多姿。也欢迎你在评论区和我交流,期待看到大家的奇思妙想。
思考题
我再给你留一道思考题:给定一个链表,请使用插入排序对这个链表排序吧。
你可以把答案写在评论区,我们一起讨论。接下来请和我一起踏上更加奇妙的算法与数据结构的旅程。让我们继续前进。下一讲将介绍 09 | 二分搜索:为什么说有序皆可用二分?记得按时来探险。

