蒙特卡洛(Monte Carlo)方法，又称随机抽样或统计试验方法。当所求解的问题是某种事件出现的概率，或某随机变量的期望值时，可以通过某种“试验”方法求解。
    简单说，蒙特卡洛是利用随机试验求解问题的方法。
    构造一个单位正方形和一个单位圆，往整个区域内随机投入点，根据点到原点的距离判断点是落在圆内还是在圆外，从而根据落在两个不同区域的点的数目，求出两个区域的比值。如此一来，就可以求出单位圆的面积，从而求出圆周率π。

    PI.png

    随机产生一对x,y的值，随机生成x,y的正负号，组成一组坐标。控制turtle走到这个坐标处画一个点，判断这个点的位置如果落在圆内，计数。绘制完成后，所以落在圆内的点与总点数的比值即是面积在比值。如果所有点都是随机产生，那么落在圆内的点和圆外的点的分布应该是基本均匀的，而且随点数的增加会趋于更均匀。即提高产生点的数量，可以获得更准确的PI值。

    1. import random
    3. n = int(input())                           # 输入一个整数，100000
    4. lsx = [random.random() for x in range(n)]  # 列表推导式随机生成n个小数
    5. lsy = [random.random() for y in range(n)]  # 列表推导式随机生成n个小数
    6. coordinate = zip(lsx, lsy)  # zip()将两个列表中对应序号的数据组成n对坐标
    7. count = 0                                  # 计数器置0
    8. for xy in coordinate:                      # zip是生成器对象，可遍历
    9.     if xy[0] ** 2 + xy[1] ** 2 <= 1:       # 判断坐标点是否落在圆内
    10.         count = count + 1                  # 落在圆内的点数量增加 1
    11. PI = 4 * count / n                         # 计算圆周率值
    12. print('{:.6f}'.format(PI))                 # 输出结果3.140920（随机结果不同）

    可以在遍历的同时进行同步赋值：

    1. import random
    3. n = int(input())                           # 输入一个整数,例如100000
    4. lsx = [random.random() for x in range(n)]  # 推导式随机生成n个小数
    5. lsy = [random.random() for y in range(n)]  # 推导式随机生成n个小数
    6. coordinate = zip(lsx, lsy)  # 将两个列表中对应序号的数据组成n对坐标
    7. count = 0                                  # 计数器置0
    8. for x, y in coordinate:                    # 可在遍历同时用同步赋值方法分别取得横纵坐标的值x,y
    9.     if x ** 2 + y ** 2 <= 1:               # 判断坐标点是否落在圆内
    10.         count = count + 1                  # 落在圆内的点数量增加 1
    11. PI = 4 * count / n                         # 计算圆周率值
    12. print('{:.6f}'.format(PI))                 # 随机结果，如3.140920

    用列表推导式产生落在圆内部的坐标的列表

    1. import random
    3. n = int(input())                           # 输入一个整数,例如100000
    4. lsx = [random.random() for x in range(n)]  # 推导式随机生成n个小数
    5. lsy = [random.random() for y in range(n)]  # 推导式随机生成n个小数
    6. coordinate = zip(lsx, lsy)  # 将两个列表中对应序号的数据组成n对坐标
    7. # 用列表推导式产生落在圆内部的坐标的列表，其长度为点的数量
    8. count = len([(x, y) for x, y in coordinate if x ** 2 + y ** 2 <= 1])
    9. PI = 4 * count / n                         # 计算圆周率值
    10. print('{:.6f}'.format(PI))                 # 随机结果，如3.140920

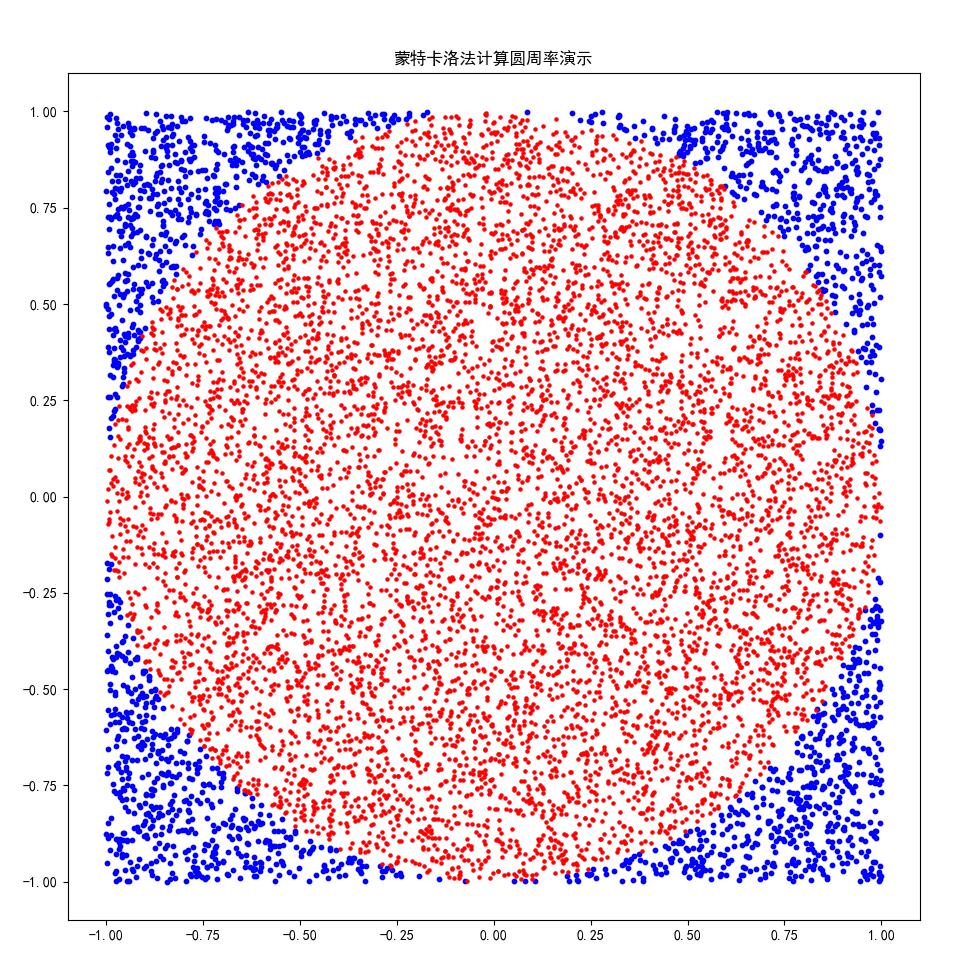
    用matplotlib绘制模拟过程

    1. import random
    2. import matplotlib.pyplot as plt
    5. def monte_carlo_pi(num):
    6.     """接收一个表示随机次数的整数，用蒙特卡洛法计算圆周率，返回一个圆周率、落在圆内点的列表和圆外点的列表"""
    7.     hits = 0  # 落在圆内的计数器初值设为 0
    8.     in_circle_lst, out_circle_lst = [],[]
    9.     for i in range(1, num + 1):
    10.         x, y = random.uniform(-1, 1), random.uniform(-1, 1),  # 生成两个随机数模拟一个点的坐标
    11.         pos = (x ** 2 + y ** 2) ** 0.5  # 计算坐标（x,y）到原点的距离
    12.         if pos <= 1.0:  # 如果距离小于等于1，点在圆内
    13.             hits = hits + 1
    14.             in_circle_lst.append([x,y])
    15.         else:
    16.             out_circle_lst.append([x,y])
    17.     pi = 4 * (hits / num)
    19.     return pi,in_circle_lst, out_circle_lst
    22. def monte_carlo_show(in_circle_lst, out_circle_lst):
    23.     """
    24.     @参数 in_circle_lst：落在圆内的点的坐标列表
    25.     @参数 out_circle_lst：落在圆外的点的坐标列表
    27.     """
    28.     plt.rcParams['font.sans-serif'] = ['SimHei']   # 用来正常显示中文标签
    29.     plt.rcParams['axes.unicode_minus'] = False     # 用来正常显示负号
    30.     plt.figure(figsize=(11, 11))                   # 设置画布长宽
    31.     x_in_circle = [x[0] for x in in_circle_lst]    # 落在圆内的点的列表x
    32.     y_in_circle = [x[1] for x in in_circle_lst]    # 落在圆内的点的列表y
    33.     x_out_circle = [x[0] for x in out_circle_lst]  # 落在圆外的点的列表x
    34.     y_out_circle = [x[1] for x in out_circle_lst]  # 落在圆外的点的列表y
    35.     plt.scatter(x_out_circle, y_out_circle, s=10, facecolors='blue')  # 绘制散点，落在圆外在点颜色用蓝色
    36.     plt.scatter(x_in_circle, y_in_circle, s=5, facecolors='red')      # 绘制散点，落在圆内在点颜色用红色
    37.     plt.title('蒙特卡洛法计算圆周率演示')  # 图的标题
    38.     plt.show()                          # 显示绘制结果
    41. if __name__ == '__main__':
    42.     pi, in_circle_ls, out_circle_ls = monte_carlo_pi(10000)  # 调用函数计算圆周率
    43.     print(pi)
    44.     monte_carlo_show(in_circle_ls, out_circle_ls)

    MC_pi.jpg
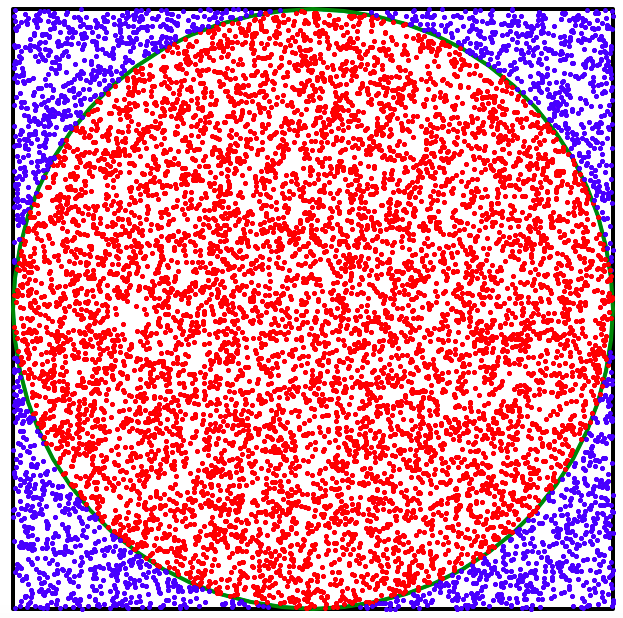
    用turtle绘制效果示意图

    1. import random                   # 导入随机数库
    2. import turtle                   # 导入turtle库
    4. s,n = map(int,input().split())
    5. random.seed(s)
    6. turtle.pensize(4)
    7. turtle.penup()
    8. turtle.goto(-400, -400)
    9. turtle.pendown()
    10. for i in range(4):
    11.     turtle.forward(800)
    12.     turtle.left(90)
    13. turtle.forward(400)
    14. turtle.pencolor('green')
    15. turtle.circle(400)
    16. hits = 0                        # 落在圆内的计数器初值设为 0
    17. turtle.tracer(0)                # 设置刷新间隔
    18. for i in range(1, n+1):
    19.     x, y = random.random(), random.random() # 生成两个随机数模拟一个点的坐标
    20.     signx,signy = random.choice('+-'),random.choice('+-')
    21. # 随机生成x和y的符号“+”或“-”
    22.     pos = (x ** 2 + y ** 2)**0.5  # 计算坐标（x,y）到原点的距离
    23.     if pos <= 1.0:                # 如果距离小于等于1，点在圆内
    24.         hits = hits + 1
    25.         turtle.pencolor('red')    # 落在圆内在点颜色用红色
    26.     else:                         # 如果距离大于1，点在圆外
    27.         turtle.pencolor('blue')   # 落在圆内在点颜色用蓝色
    28.     x = float(signx+str(x))       # 将 x 值与符号拼接并转为浮点数
    29.     y = float(signy+str(y))       # 将 y 值与符号拼接并转为浮点数
    30.     turtle.penup()
    31.     turtle.goto(x * 400, y * 400) # 画笔抬起并移动到数值放大400倍的x,y处
    32.     turtle.pendown()
    33.     turtle.dot(5)                 # 画一个半径为 3 的圆点
    34.     if i % 1000 == 0:             # 实验为10000的倍数次时
    35.        turtle.pencolor('black')
    36.        pi = 4 * (hits / i)        # 根据落在圆内外的点数量估算PI值
    37.        turtle.penup()             # 画笔抬起
    38.        turtle.goto(420, 200- i // 1000 * 30)  # 移动到区域外记录当前PI值
    39.        turtle.pendown()           # 画笔抬起
    40.        turtle.write("{}次时PI的值是{:.4f}".format(i,pi),font=("宋体", 18, "normal"))
    41. turtle.update()                   # 刷新
    42. turtle.hideturtle()               # 隐藏光标
    43. turtle.done()                     # 结束绘制

    PI.gif