描述
写一个函数isPrime(n)用于判断一个数字n是不是素数，用户输入一个正整数，在一行内输出不大于该数的所有素数，各数后面用一个空格分隔。
输入格式
输入一个正整数
输出格式
不大于该数的所有素数，各数后面用一个空格分隔。
输入输出示例

|

输入 输出
示例 1 100 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

解析：
素数的概念又称为质数，一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数。
可以定义一个函数，传入一个整数，返回其是否为素数。判定一个数是否为素数的方法是，用传入的整数 n 除从2到n-1之间的每一个整数，如果存在某个可以整除的数，则其不是素数，如果没有任何除1和其本身以外的因子，则其是素数。（时间复杂度为o(n)）

  1. # 将判断一个整数 n 是否为素数的代码定义为一个函数isPrime(n)
  2. # 传入参数为整数 n，n 是素数时返回值为True，否则返回False
  3. # 时间复杂度为o(n)
  4. def is_prime(n):  # 判断参数 n 是否为素数的函数
  5.     """判断素数，接受一个正整数n为参数，判断n是否为素数，返回布尔值"""
  6.     if n <= 1:   # 小于2的数字都不是素数
  7.         return False
  8.     for i in range(2,n):   # 根据素数定义判定是否是素数，是素数返回1
  9.         if n % i == 0:     # 从 2到n-1中如果存在一个数是i，使n 可以整除i，则n不是素数
  10.             return False
  11.     else:                  # 若for循环未遇到return正常结束，则n是素数
  12.         return True
  15. # 以下代码调用定义的isPrime()判定num是否为素数，输出小于m的所有素数
  16. m = int(input())               # 输入一个正整数
  17. for num in range(m):           # 获得小于m的整数数列
  18.     if is_prime(num):          # 如果isPrime(num)返回值为True,num 是素数
  19.         print(num, end=' ')   # 输出num
  22. # 输入 100
  23. # 输出 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
  1. 其主程序部分可以修改为以下模式，使当前文件可以做为模块被其他程序调用。当文件直接被运行时，if __name__ == "__main__":语句后的语句块中的输入输出等语句会被执行。当文件被当做模块import时，只调用其中的函数，if __name__ == "__main__":后的语句块不会被执行。

  • ```python

    将判断一个整数 n 是否为素数的代码定义为一个函数isPrime(n)

    传入参数为整数 n，n 是素数时返回值为True，否则返回False

    时间复杂度为o(n)

    def is_prime(n): # 判断参数 n 是否为素数的函数 “””判断素数，接受一个正整数n为参数，判断n是否为素数，返回布尔值””” if n <= 1: # 小于2的数字都不是素数
    1.   return False
    for i in range(2,n): # 根据素数定义判定是否是素数，是素数返回1
      if n % i == 0:     # 从 2到n-1中如果存在一个数是i，使n 可以整除i，则n不是素数
      return False
    else: # 若for循环未遇到return正常结束，则n是素数
      return True

name 是当前模块名，当模块被直接运行时模块名为 main 。

当模块被直接运行时，以下代码块将被运行，当模块是被导入时，代码块不被运行。

可以删除if name == “main“:，将下面语句块向前提一级

以下代码调用定义的isPrime()判定num是否为素数，输出小于m的所有素数

if name == “main“: m = int(input()) # 输入一个正整数 for num in range(m): # 获得小于m的整数数列 if isPrime(num): # 如果is_prime(num)返回值为True,num 是素数 print(num,end=’ ‘) # 输出num

输入 100

输出 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

    我们知道一个数若可以进行因数分解，那么分解时得到的两个数一定是一个小于等于sqrt(n)，一个大于等于sqrt(n)，所以对于每个数n，并不需要从2判断到n-1，遍历到sqrt(n)即可。因为若sqrt(n)左侧找不到约数，那么右侧也一定找不到约数。这样可以显著提升算法的效率，上面判断素数函数可以修改为：

```python
# 传入参数为整数 n，n 是素数时返回值为True，否则返回False
# 时间复杂度为o(n)
def is_prime(n):  # 判断参数 n 是否为素数的函数
    """判断素数，接受一个正整数n为参数，判断n是否为素数，返回布尔值"""
    if n <= 1:   # 小于2的数字都不是素数
        return False
    for i in range(2, int(n ** 0.5) + 1):   # 根据素数定义判定是否是素数，是素数返回1
        if n % i == 0:     # 从 2到n的平方根之间中如果存在一个数是i，使n 可以整除i，则n不是素数
            return False
    else:                  # 若for循环未遇到return正常结束，则n是素数
        return True

依据经验，我们知道素数分布的规律，除了2以外的所有素数都是奇数，所以可以只判定奇数是否是素数就可以，可以减少一半的判定素数的计算量。

def check_prime(n):
    if n > 2:
        print(2, end=' ')
    for num in range(3, n, 2):  # 获得小于n的整数数列
        if is_prime(num):  # 如果is_prime(num)返回值为True,num 是素数
            print(num, end=' ')  # 输出num

素数分布的规律：大于等于5的素数一定和6的倍数相邻。例如5和7，11和13,17和19等等。<br />查看100以内的素数：<br />2 3   5 7    11 13    17 19    23    29 31    37    41 43    47 53    59 61   67    71 73    79 83 89 97<br />   可以发现除2和3外，其他数都是6的倍数的相邻数：<br />6-1，6+1，2*6-1，2*6+1，3*6-1，3*6+1...<br />    但要注意，6 的倍数的相邻数并不全是素数，例如35。所以还是需要调用素数判定函数进行判定。只判定6的倍数的相邻数是否是素数就可以找到所有素数。这样可以进一步减少判定的次数，提高效率。注意2、3和5要单独判定。

def check_prime(n):
    if n > 2:
        print(2, end=' ')
    if n > 3:
        print(3, end=' ')
    if n > 5:
        print(5, end=' ')
    for num in range(0, n, 6):       # 获得小于m的整数数列
        if is_prime(num - 1):         # 如果is_prime(num -1)返回值为True,num 是素数
            print(num - 1, end=' ')  # 输出num - 1
        if is_prime(num + 1) and (num + 1) < n:  # 如果is_prime(num + 1)返回值为True,num 是素数
            print(num + 1, end=' ')  # 输出num + 1

   综合以上分析，可以同时优先判定素数的函数和判定的代码：

def is_prime(n):  # 判断参数 n 是否为素数的函数
    """判断素数，接受一个正整数n为参数，判断n是否为素数，返回布尔值"""
    if n <= 1:      # 小于2的数字都不是素数
        return False
    for i in range(2, int(n ** 0.5) + 1):   # 两因子相同时，为保证取到右边界，需加1
    # for i in range(2, int(math.sqrt(n)) + 1)
        if n % i == 0:            
            return False
    else:                          # 若for循环未遇到return正常结束，则n是素数
        return True


def check_prime(n):
    if n > 2:
        print(2, end=' ')
    if n > 3:
        print(3, end=' ')
    if n > 5:
        print(5, end=' ')
    for num in range(0, n, 6):       # 获得小于m的整数数列
        if is_prime(num - 1):         # 如果is_prime(num -1)返回值为True,num 是素数
            print(num - 1, end=' ')  # 输出num - 1
        if is_prime(num + 1) and (num + 1) < n:  # 如果is_prime(num + 1)返回值为True,num 是素数
            print(num + 1, end=' ')  # 输出num + 1


# def check_prime(n):
#     if n > 2:
#         print(2, end=' ')
#     for num in range(3, n, 2):  # 获得小于n的整数数列
#         if is_prime(num):  # 如果is_prime(num)返回值为True,num 是素数
#             print(num, end=' ')  # 输出num


if __name__ == "__main__":
    m = int(input())                # 输入一个正整数
    check_prime(m)

    除了这些方法以外，还可以使用筛选法，先生成小于n的所有数字，再把 2 到 sqrt(n) 之间的整数的倍数依次去掉，剩余的就是小于n的所有素数了。这种方法的效率更高<br />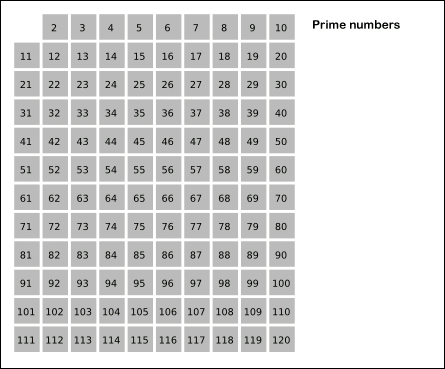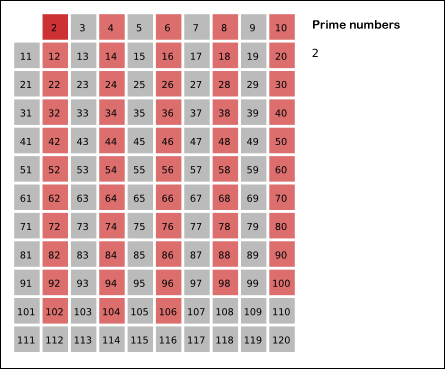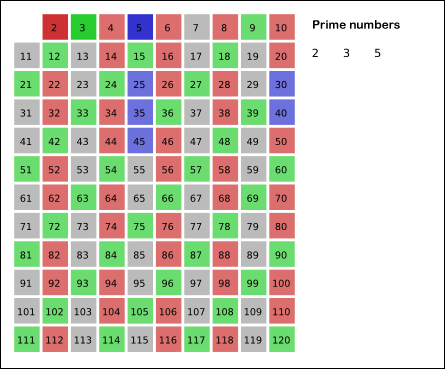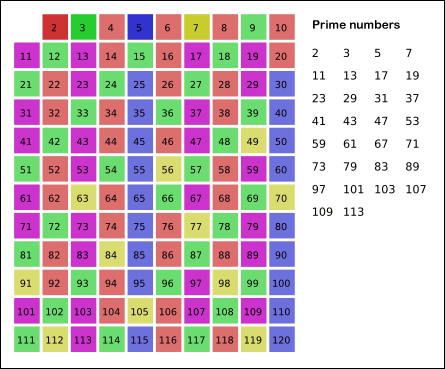![](https://cdn.nlark.com/yuque/0/2020/gif/1157448/1584803967610-868391c1-a29a-4768-b783-4386050ac626.gif#height=369&id=ocyCD&originHeight=369&originWidth=445&originalType=binary&ratio=1&size=0&status=done&style=none&width=445)<br />（注：此图片来自网络，版权归原作者所有，此处仅用于教学演示）

def is_prime(n):
    """筛选法获取小于n的所有素数"""
    ls = list(range(3, n, 2))  # 待判断整数
    for index in range(int(n ** 0.5)):  # 最大整数的平方根
        current = ls[index]
        if current > int(n ** 0.5):  # 如果当前数字已大于最大整数的平方根，结束判断
            break
        # 对该位置之后的元素进行过滤
        ls[index + 1:] = list(filter(lambda x: 0 if not x % current else x, ls[index + 1:]))
    return [2] + ls  # 2是素数，单独加上去


print(*is_prime(120))  # 输出120以内所有素数

如果不考虑效率和易读性，可以用一条语句实现素数的输出：

print(*[x for x in range(2, int(input())) if not [y for y in range(2, x) if x % y == 0]])

100
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97