1.割圆法计算圆周率

  1. """用正六边形近似圆，计算圆周率
  2. π = 周长/(2*圆的半径)得到π的近似值。
  3. # 半径为1的圆内接正6边形边长也是1
  4. # 边长  side_length
  5. # 半径  radius
  6. # 圆周率 pi
  7. # 三角形的高 height
  8. """
  9. side_length = 1          # 初始边长
  10. edges = 6                # 初始边数
  11. height = 1 - math.sqrt(1 - (side_length / 2) ** 2)
  12. side_length = math.sqrt(height ** 2 + (side_length / 2) ** 2)
  13. pi = side_length * edges
  14. print(pi)  # 3.105828541230249

2.割圆法计算圆周率（思政，中华文明，精益求精）

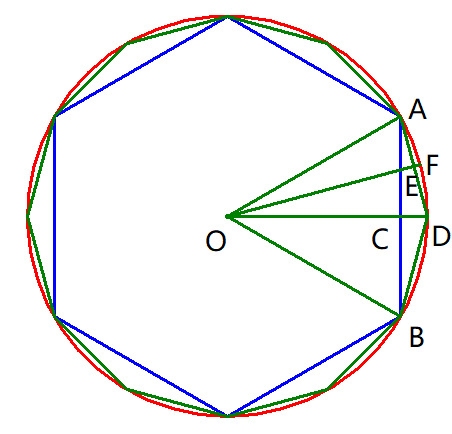
image.png

  1. import math
  4. def cutting_circle(times):
  5.     """参数times为分割次数
  6.     π = 周长/(2*圆的半径)得到π的近似值。
  7.     # 半径为1的圆内接正6边形边长也是1
  8.     # 边长  side_length
  9.     # 半径  radius
  10.     # 圆周率 pi
  11.     # 三角形的高 height
  12.     """
  13.     side_length = 1  # 初始边长
  14.     edges = 6        # 初始边数
  15.     for i in range(times):
  16.         height = 1 - math.sqrt(1 - (side_length / 2) ** 2)
  17.         side_length = math.sqrt(height ** 2 + (side_length / 2) ** 2)
  18.         edges = edges * 2  # 每割一次，边数量加倍
  19.     pi = side_length * edges / 2
  20.     return pi
  23. if __name__ == '__main__':
  24.     print(cutting_circle(2))   # 3.1326286132812378
  25.     print(cutting_circle(20))  # 3.141592653589663

3.莱布尼茨级数计算圆周率

数学思维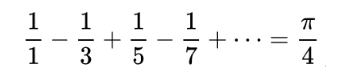
image.png

  1. def leibniz_of_pi(error):
  2.     """接收用户输入的浮点数阈值为参数，用格雷戈里-莱布尼茨级数计算圆周率，返回圆周率值"""
  3.     n, quarter_of_pi, sign = 1, 0, 1
  4.     while 1 / (2 * n - 1) > error:
  5.         quarter_of_pi = quarter_of_pi + sign * 1 / (2 * n - 1)
  6.         n = n + 1
  7.         sign = -sign
  8.     pi = 4 * quarter_of_pi
  9.     return pi
  12. if __name__ == '__main__':
  13.     print(leibniz_of_pi(1e-6))  # 3.141590653589692

4.蒙特卡洛法计算圆周率

统计方法，蒙特卡洛算法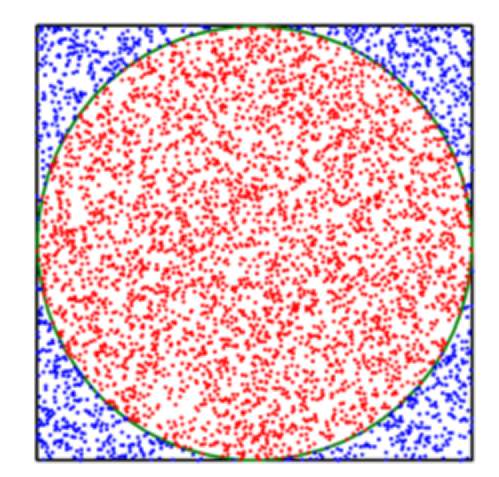
image.png

  1. import random
  4. def monte_carlo_pi(num):
  5.     """接收一个表示随机次数的整数，用蒙特卡洛法计算圆周率，返回一个浮点数"""
  6.     hits = 0                            # 落在圆内的计数器初值设为 0
  7.     for i in range(1, num + 1):
  8.         x, y = random.uniform(-1, 1), random.uniform(-1, 1),  # 生成两个随机数模拟一个点的坐标
  9.         pos = (x ** 2 + y ** 2) ** 0.5  # 计算坐标（x,y）到原点的距离
  10.         if pos <= 1.0:                  # 如果距离小于等于1，点在圆内
  11.             hits = hits + 1
  12.     pi = 4 * (hits / num)
  13.     return pi
  16. if __name__ == '__main__':
  17.     print(monte_carlo_pi(1000000))  # 3.142968

5.梅钦级数计算圆周率

数学思维，效率意识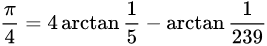
image.png

  1. import math
  4. def machin_of_pi():
  5.     """用梅钦级数计算圆周率，返回圆周率值"""
  6.     quarter_of_pi = 4 * math.atan(1/5) - math.atan(1/239)
  7.     pi = 4 * quarter_of_pi
  8.     return pi
  11. if __name__ == '__main__':
  12.     print(machin_of_pi())  # 3.1415926535897936

6.拉马努金公式计算圆周率

数学思维，效率意识，循环在数学中的应用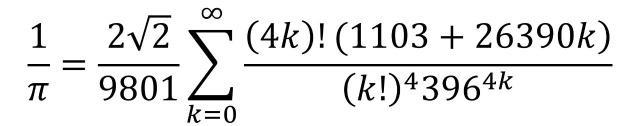
image.png

  1. import math
  4. def ramanujan_of_pi(n):
  5.     """接收一个正整数n为参数，用拉马努金公式的前n项计算圆周率并返回。"""
  6.     result = 0
  7.     for i in range(n):
  8.         result = result + ((2 * 2 ** 0.5)) * (math.factorial(4 * i) * (1103 + 26390 * i)) / (
  9.                     math.pow(math.factorial(i), 4) * math.pow(396, 4 * i)) / 9801
  10.     pi = 1 / result
  11.     return pi
  14. if __name__ == '__main__':
  15.     print(ramanujan_of_pi(2))  # 3.1415926535897936

7.演示割圆法

可视化，函数

  1. def draw_circle(r, side_num):
  2.     """创建图形和轴，用折线图绘制正多边形。
  3.     @参数 r：圆的半径
  4.     @参数 side_num：正多边形的边数
  5.     """
  6.     fig, ax = plt.subplots()           # 创建图形和轴
  7.     plt.subplots_adjust(left=0.1, bottom=0.25)
  8.     x, y = xy_of_polygon(r, side_num)
  9.     plt.plot(x, y, lw=2, color='red')  # 设置线宽和颜色
  10.     ax.set_aspect('equal')             # 设置坐标轴纵横比相等
  11.     ax.set_xlim(-r-5, r+5)             # 设置x轴刻度起止值
  12.     ax.set_ylim(-r-5, r+5)
  13.     plt.draw()                         # 重新绘制多边形
  14.     plt.show()                         # 显示图形
  17. def cutting_circle(times):
  18.     """
  19.     接收表示分割次数的整数n 为参数，计算分割n 次时正多边形的边数和圆周率值，返回边数和圆周率值。
  20.     @参数 times：分割次数
  21.     π = 周长/(2*圆的半径)得到π的近似值。
  22.     # 半径为1的圆内接正6边形边长也是1
  23.     # 边长  side_length
  24.     # 半径  radius
  25.     # 圆周率 pi
  26.     # 三角形的高 height
  27.     >>> cutting_circle(4)
  28.     3.14103195089051
  29.     """
  30.     side_length = 1          # 初始边长
  31.     edges = 6                # 初始边数
  32.     for i in range(times):
  33.         height = 1 - math.sqrt(1 - (side_length / 2) ** 2)
  34.         side_length = math.sqrt(height ** 2 + (side_length / 2) ** 2)
  35.         edges = edges * 2          # 每割一次，边数量加倍
  36.         draw_circle(300, edges)  # 调用此函数可演示割圆效果，每次循环绘制一个近似圆，关闭后看下一个
  37.     pi = side_length * edges / 2
  38.     return pi

8.matplotlib演示蒙特卡洛

  1. import matplotlib.pyplot as plt
  3. def monte_carlo_show(in_circle_lst, out_circle_lst):
  4.     """
  5.     @参数 in_circle_lst：落在圆内的点的坐标列表
  6.     @参数 out_circle_lst：落在圆外的点的坐标列表
  8.     """
  9.     plt.rcParams['font.sans-serif'] = ['SimHei']   # 用来正常显示中文标签
  10.     plt.rcParams['axes.unicode_minus'] = False     # 用来正常显示负号
  11.     plt.figure(figsize=(11, 11))                   # 设置画布长宽
  12.     x_in_circle = [x[0] for x in in_circle_lst]    # 落在圆内的点的列表x
  13.     y_in_circle = [x[1] for x in in_circle_lst]    # 落在圆内的点的列表y
  14.     x_out_circle = [x[0] for x in out_circle_lst]  # 落在圆外的点的列表x
  15.     y_out_circle = [x[1] for x in out_circle_lst]  # 落在圆外的点的列表y
  16.     plt.scatter(x_out_circle, y_out_circle, s=10, facecolors='blue')  # 绘制散点，落在圆外在点颜色用蓝色
  17.     plt.scatter(x_in_circle, y_in_circle, s=5, facecolors='red')    # 绘制散点，落在圆内在点颜色用红色
  18.     plt.title('蒙特卡洛法计算圆周率演示')             # 图的标题
  19.     plt.show()                                     # 显示绘制结果

9.turtle演示蒙特卡洛

  1. import turtle
  3. # 给出turtle模板，学生填monte_carlo代码，帮助学生理解算法，了解turtle绘图
  4. def monte_carlo_pi_turtle(n, s):
  5.     """用turtle绘图模拟蒙特卡洛n次结果"""
  6.     random.seed(s)
  7.     turtle.tracer(1000)
  8.     turtle.pensize(4)
  9.     turtle.penup()
  10.     turtle.goto(-300, -300)
  11.     turtle.pendown()
  12.     for i in range(4):
  13.         turtle.forward(600)
  14.         turtle.left(90)
  15.     turtle.forward(300)
  16.     turtle.pencolor('green')
  17.     turtle.circle(300)
  18.     hits = 0  # 落在圆内的计数器初值设为 0
  19.     for i in range(1, n + 1):
  20.         x, y = random.uniform(-1, 1), random.uniform(-1, 1)  # 生成两个随机数模拟一个点的坐标
  21.         pos = (x ** 2 + y ** 2) ** 0.5                       # 计算坐标（x,y）到原点的距离
  22.         if pos <= 1.0:                                       # 如果距离小于等于1，点在圆内
  23.             hits = hits + 1
  24.             turtle.pencolor('red')                           # 落在圆内在点颜色用红色
  25.         else:                                                # 如果距离大于1，点在圆外
  26.             turtle.pencolor('blue')                          # 落在圆内在点颜色用蓝色
  27.         turtle.penup()
  28.         turtle.goto(x * 300, y * 300)                        # 画笔抬起并移动到数值放大400倍的x,y处
  29.         turtle.pendown()
  30.         turtle.dot(3)                                        # 画一个半径为 3 的圆点
  31.         if i % 10000 == 0:                                   # 实验为10000的倍数次时
  32.             turtle.pencolor('black')
  33.             pi = 4 * (hits / i)                              # 根据落在圆内外的点数量估算PI值
  34.             turtle.penup()                                   # 画笔抬起
  35.             turtle.goto(320, 150 - i // 1000 * 30)           # 移动到区域外记录当前PI值
  36.             turtle.pendown()                                 # 画笔抬起
  37.             turtle.write("{}次时PI的值是{:.4f}".format(i, pi), font=("宋体", 18, "normal"))
  38.     turtle.hideturtle()  # 隐藏光标
  39.     turtle.update()      # 刷新
  40.     turtle.done()        # 结束绘制