1. 兔子繁殖问题

兔子从出生后第3个月起每个月都会生一对兔子，小兔子成长到第三个月后每个月又会生一对兔子。初始有一对小兔子，假如兔子都不死，用户输入一个月份数，计算并在一行内输出从1到n月每个月的兔子数量。


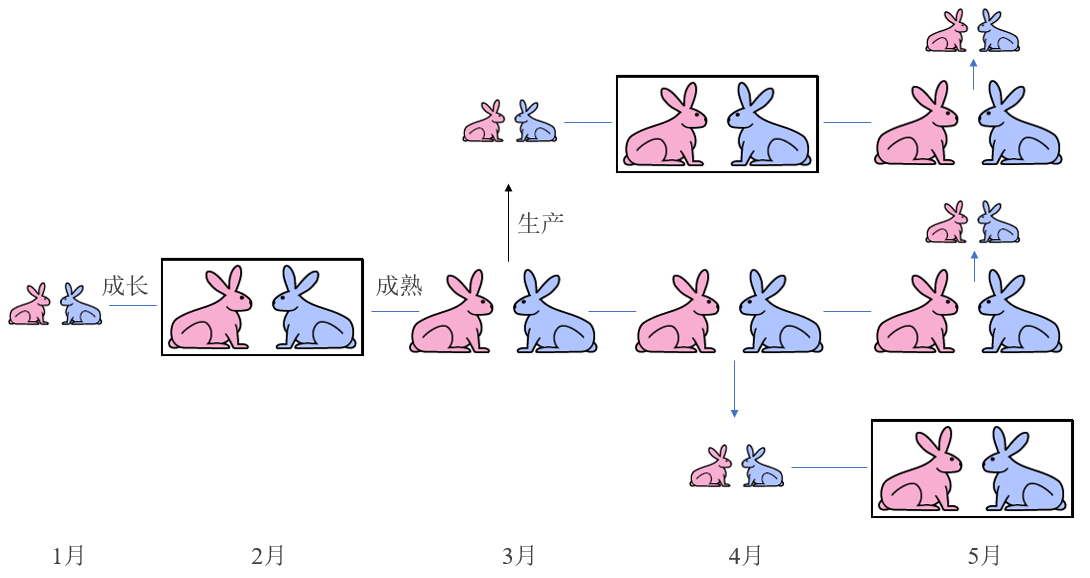
图 3.3 兔子繁殖规律

各月的兔子数量形成的数列是：
1，1，2，3，5，8，13，……
斐波那契数列以如下被以递推的方法定义：
F(1)=1
F(2)=1
F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）
计算a，b指向数据的和作为新的一项，同时将变量b指向新产生的数据项，将变量a指向倒数第二项，也就是原来变量b指向的那个数据，这个操作可以用同步赋值语句a,b=b,a+b实现。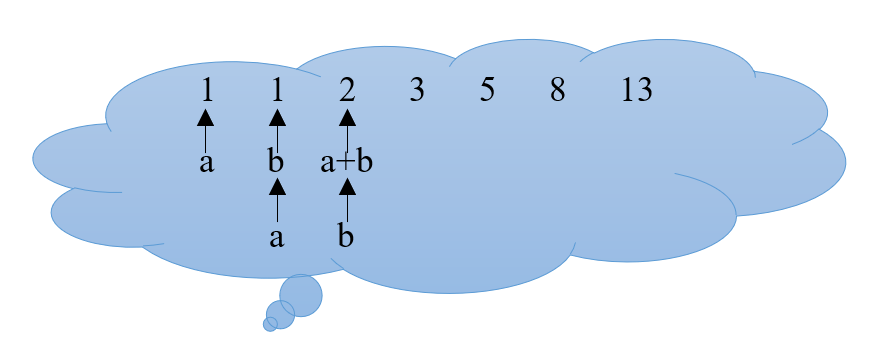

图 3.4 变量同步赋值

n = int(input())       # int()将input()接收的字符串转整数,例如输入12
a, b = 1, 1            # 设定数列前两项的初值
for i in range(n):     # i 只用于控制循环次数,n值为12
    print(a, end=' ')  # 每次循环输出一个值，不换行
    a, b = b, a + b    # b的值赋给a，把a，b的和赋值给b
# 1 1 2 3 5 8 13 21 34 55 89 144

2. 迭代法开平方

import math
x = int(input())             # 输入整数
x1 = x / 2                   # 初值
x2 = (x1 + x / x1) / 2       # 迭代公式
while abs(x1 - x2) > 1e-5:   # 迭代精度
    x1 = x2
    x2 = (x1 + x / x1) / 2
print(x2)            # 2.23606797749979
print(math.sqrt(x))  # 2.23606797749979

3. 牛顿迭代法

牛顿迭代法解 一元三次方程 x³－2x＋1＝0，给定误差 0.0001

def f(x):
    """f的方程"""
    return x ** 3 - 2 * x + 1
def f_first_order(x):
    """f的一阶导数"""
    return 3 * x ** 2 - 2
def get_root(x0, max_iter=50, tol=1e-5):
    """将初始值浮点化"""
    p0 = x0
    for i in range(max_iter):
        p = p0 - f(p0) / f_first_order(p0)  # f的一阶导数不能为0
        if abs(p - p0) < tol:               # 如果小于精度值则退出迭代
            return f'经{i}次迭代，估计参数值是{p:.3f}'
        p0 = p
    print('达到最大迭代次数，无法收敛')
if __name__ == '__main__':
    print(get_root(2))   # 经6次迭代，估计参数值是1.000
    print(get_root(0))   # 经4次迭代，估计参数值是0.618
    print(get_root(-2))  # 经4次迭代，估计参数值是-1.618