“matplotlib.pyplot”模块是一组命令式函数的集合，使 “matplotlib ”
    的工作方式类似于MATLAB。

    每个“pyplot”函数都会对图形做某些更改：例如创建图形、在图形中创建绘图区域、在绘图区域中绘制一些线、用标签装饰绘图等。
    在模块“matplotlib.pyplot”中跨函数调用的各种状态被保留下来，以便跟踪当前图形和绘图区域，以及绘图功能指向当前轴（请注意此处的“轴”在文档中的大多数地方都是指图形的一部分，而数学术语中对一个以上轴的严格定义）。
    pyplot API通常不如面向对象API灵活。这里看到的大多数函数也可以作为“Axes”对象的方法调用。我们建议通过浏览教程和示例了解其如何工作。

    使用pyplot生成可视化效果非常快：

    1. import matplotlib.pyplot as plt
    3. plt.plot([1, 2, 3, 4])       # 只有一个参数时，被做为 y ,系统自动产生等长度的 x 整数数列
    4. plt.ylabel('some numbers')   # y 轴标签
    5. plt.show()                   # 显示绘制结果

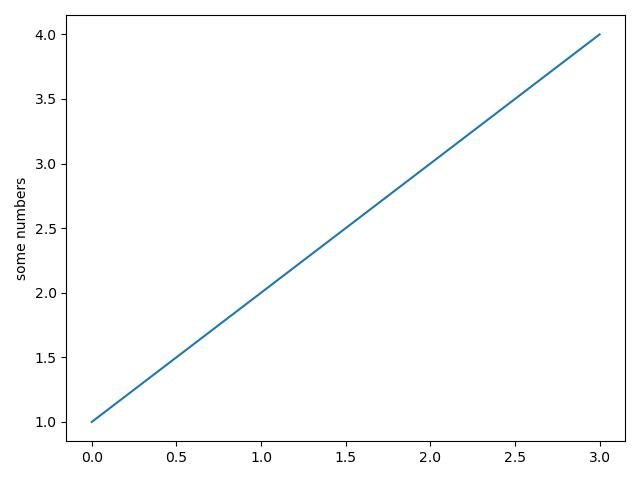
    image.png

    你可能奇怪为什么x轴的范围是0-3而y轴从1到4？这是因为如果只有一个参数的话， matplotlib 假定它是 y 值序列，并自动生成 x 序列。由于 python 范围默认从 0 开始，若使 x 向量长度与 y 相同，产生的从 0 开始的 x 数据应是 [0，1，2，3]。
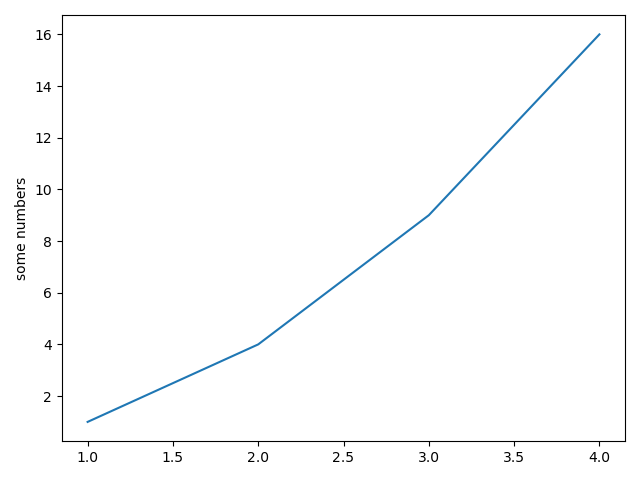
    绘制 y = x 可以用以下方法：

    1. import matplotlib.pyplot as plt
    3. plt.plot([1, 2, 3, 4], [1, 4, 9, 16])  # y 的列表的值均是 x 列表元素的平方 
    4. plt.ylabel('some numbers')
    5. plt.show()

    image.png
    设置绘制风格：
    对于每个 x,y 参数对，都有一个可选的第三个参数，这个参数是一个字符串，用于指明绘制颜色和线型，默认格式字符串为“b-”，这是一条蓝色实线。

    例如，要用红色圆圈绘制上述图型，可以如一上修改代码：

    1. import matplotlib.pyplot as plt
    3. plt.plot([1, 2, 3, 4], [1, 4, 9, 16], 'ro')  # 'ro' 表示 红色 red 圆点
    4. plt.axis([0, 6, 0, 20])                      # 设定坐标刻度，前2个参数为x范围，后2个参数为y范围
    5. plt.show()

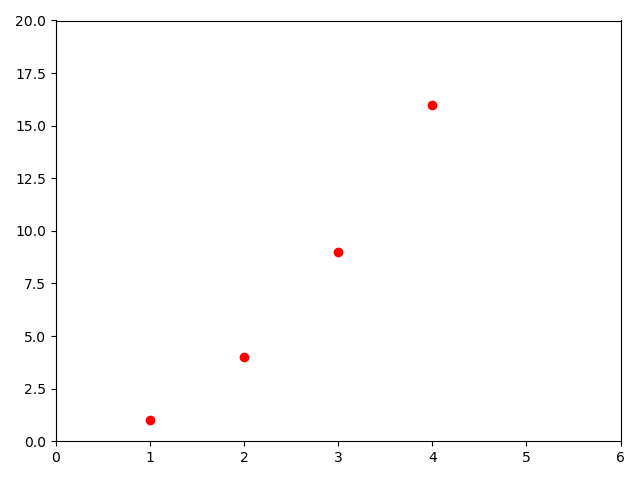
    image.png

    上面示例中的函数：“matplotlib.pyplot.axis”命令获取一个形如 [xmin，xmax，ymin，ymax]的列表，并指定轴的范围。如果matplotlib仅限于处理列表，那么对于数值处理来说它将的应用将大打折扣。通常，我们将使用“numpy” 数组。实际上，所有序列都在内部转换为numpy数组。下面的示例演示如何使用数组在一个命令中绘制具有不同格式样式的多条线。

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    4. # np.arange(0., 5., 0.2) 从 0-5间隔0.2产生数组
    5. t = np.arange(0., 5., 0.2)
    6. # [0.  0.2 0.4 0.6 0.8 1.  1.2 1.4 1.6 1.8 2.  2.2 2.4 2.6 2.8 3.  3.2 3.4
    7. #  3.6 3.8 4.  4.2 4.4 4.6 4.8]
    9. # 'r--' 红色虚线
    10. # 'bs', 蓝色方块
    11. #  'g^' 绿色向上三角
    12. plt.plot(t, t, 'r--', t, t**2, 'bs', t, t**3, 'g^')
    13. plt.show()

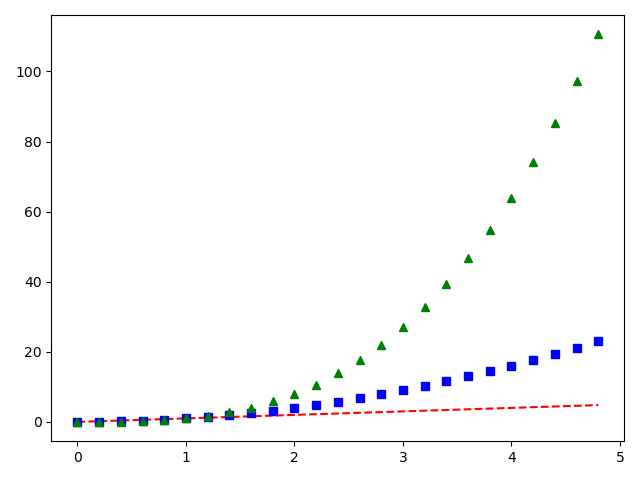
    image.png

    用关键字字符串为参数绘图
    有些情况下，参数数据中允许您使用字符串访问特定变量。例如，使用类“numpy.recarray”或“pandas.DataFrame”。Matplotlib允许使用“data”关键字参数提供这样的对象。如果这样提供，则可以使用与这些字符串对应的变量中的值生成绘图。

    1. import numpy as np
    3. data = {'a': np.arange(50),
    4.         'c': np.random.randint(0, 50, 50),
    5.         'd': np.random.randn(50)}
    6. print(data)

    data 中的数据如下：

    1. {'a': array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
    2.        17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
    3.        34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49]), 
    4.  'c': array([10, 27, 33, 12, 40, 39,  5, 12, 46, 20, 28, 48, 35,  6, 45, 14,  5,
    5.        35, 18, 30, 19, 11, 33, 24, 32, 22, 33, 42, 41, 15, 44, 48, 41, 32,
    6.        25, 35, 23, 22, 26, 28,  6, 14, 19, 49, 12, 20, 46, 24, 49, 27]), 
    7.  'd': array([ 0.84466902,  0.69024905,  0.69389536,  0.4807186 , -1.3889178 ,
    8.         0.0181811 , -0.7276035 , -0.22580276, -0.7744225 ,  0.79501275,
    9.        -0.56893705,  2.17196344,  1.21731035, -0.26116256, -0.92828405,
    10.         0.12441069,  0.44413622,  0.23573053, -0.29062946, -0.63795808,
    11.        -0.35451832, -1.2738009 , -0.87293987,  0.2742025 , -1.29355815,
    12.        -0.08004296,  1.2560302 , -0.08598915,  0.64823028, -0.71970811,
    13.         0.72946779,  0.30400105,  0.98191682, -0.29503949, -1.72055046,
    14.         0.50741791, -1.45329753,  0.80902074,  0.67962089, -0.96918614,
    15.        -1.00890895, -0.0774626 , -0.44854764, -0.03985451,  1.70833952,
    16.         1.87580209,  1.64361477, -1.54353957,  0.81869733,  0.011085  ])}
    1. import numpy as np
    3. data = {'a': np.arange(50),
    4.         'c': np.random.randint(0, 50, 50),
    5.         'd': np.random.randn(50)}
    6. data['b'] = data['a'] + 10 * np.random.randn(50)
    7. data['d'] = np.abs(data['d']) * 100
    8. print(data['a'])
    9. print(data['b'])

    data[‘a’] 和 data[‘b’] 的数据如下：

    1. [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
    2.  24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
    3.  48 49]
    5. [  6.97214168 -10.380282    -7.68217561  14.33955788  11.86894138
    6.   18.33143408  -7.6186231    9.0793785   15.22721995   5.64379319
    7.   12.00400728  23.77278708  29.87295086  19.62795769  15.89583594
    8.   15.8987296   11.5689869   21.91633076   3.8127793   30.44940607
    9.    7.14658508  14.03773593   4.71170718  29.79653316  27.39539178
    10.   25.03005335   9.50755493  21.65090011   9.96919222  40.56175253
    11.   40.23138777  15.5886332   27.23770981  26.58972315  46.40630264
    12.   30.77081332  22.40096832  30.94126728  42.03587105  58.31077157
    13.   34.13848267  35.03394398  63.12716674  40.77609372  46.69172724
    14.   48.14300611  54.75090084  53.50519622  38.87581105  29.31006357]
    1. import numpy as np
    2. import matplotlib.pyplot as plt
    4. data = {'a': np.arange(50),
    5.         'c': np.random.randint(0, 50, 50),
    6.         'd': np.random.randn(50)}
    7. data['b'] = data['a'] + 10 * np.random.randn(50)
    8. data['d'] = np.abs(data['d']) * 100
    9. plt.scatter('a', 'b', c='c', s='d', data=data)  # 以字符串为参数，但字符串是数组的索引标签
    10. plt.xlabel('entry a')
    11. plt.ylabel('entry b')
    12. plt.show()

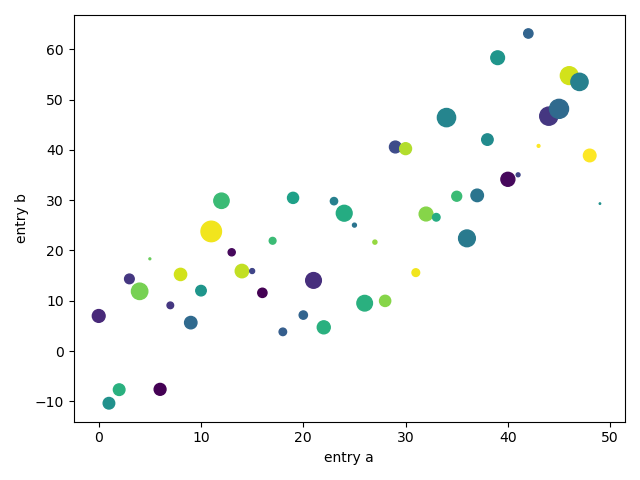
    image.png
    用分类变量绘图

    也可以使用分类变量创建绘图。Matplotlib允许您将分类变量直接传递给许多绘图函数。例如：

    1. import matplotlib.pyplot as plt
    3. names = ['group_a', 'group_b', 'group_c']
    4. values = [1, 10, 100]
    5. plt.figure(figsize=(9, 3))
    7. plt.subplot(131)            # 设置 1 * 3个子图，当前图在序号为1 的位置
    8. plt.bar(names, values)      # 利用name values列表中的值绘制柱形图
    10. plt.subplot(132)            # 设置 1 * 3个子图，当前图在序号为2 的位置
    11. plt.scatter(names, values)  # 利用name values列表中的值绘制散点图
    13. plt.subplot(133)            # 设置 1 * 3个子图，当前图在序号为3 的位置
    14. plt.plot(names, values)     # 利用name values列表中的值绘制线型图
    16. plt.suptitle('Categorical Plotting')   # 设置图的标题
    17. plt.show()

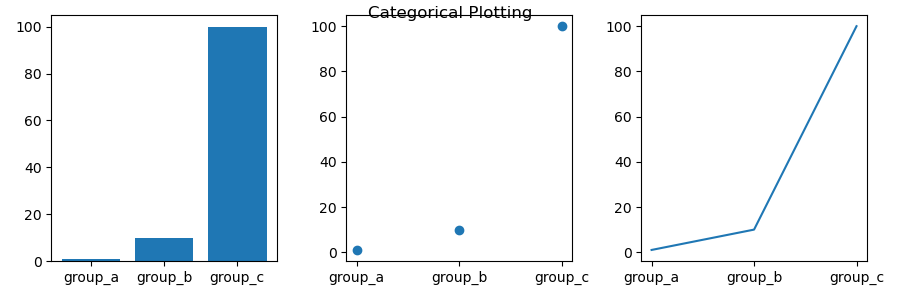
    image.png

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    4. def f(t):                                 # 定义一个函数
    5.     return np.exp(-t) * np.cos(2*np.pi*t)
    7. t1 = np.arange(0.0, 5.0, 0.1)             # 产生0-5，步长0.1的数列
    8. t2 = np.arange(0.0, 5.0, 0.02)            # 产生0-5，步长0.02的数列
    10. plt.figure()
    11. plt.subplot(211)                          # 设置2 * 1的子图，当前在序号为 1 的子图绘制    
    12. plt.plot(t1, f(t1), 'bo', t2, f(t2), 'k') # 同时绘制一个用蓝色圆点表示一个用线表示的f函数曲线
    14. plt.subplot(212)                          # 设置2 * 1的子图，当前在序号为 2 的子图绘制 
    15. plt.plot(t2, np.cos(2*np.pi*t2), 'r--')   # 绘制一个用红色虚线表示的 cos 函数曲线
    16. plt.show()

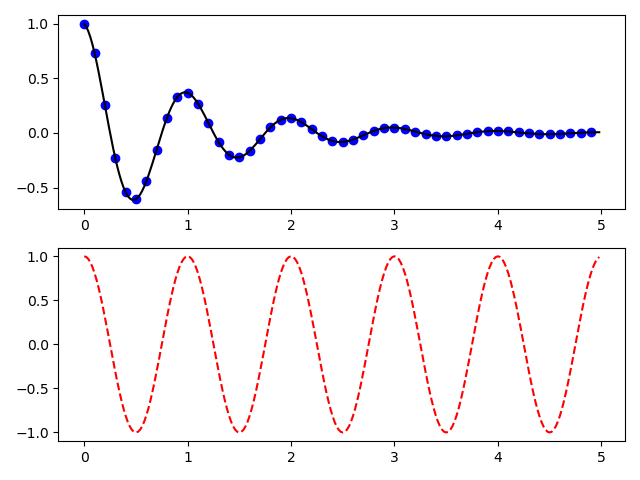
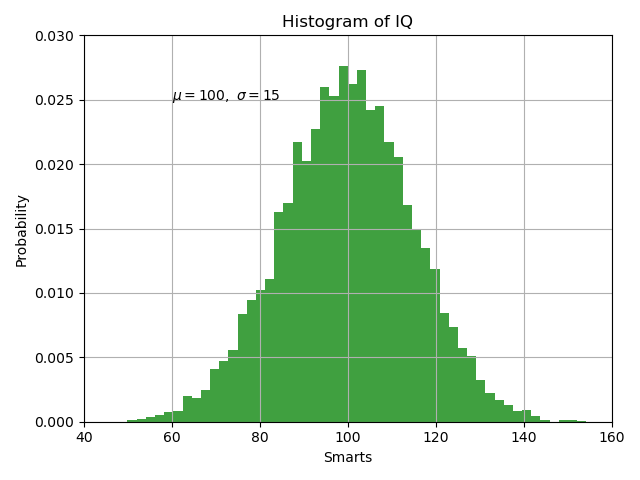
    image.png
    matplotlib接受任何文本表达式中的 TeX 表达式。例如，要在标题中编写表达式：math:`\sigma_i=15’，可以编写一个由美元符号包围的 TeX 表达式：r’$\sigma_i=15$’
    标题字符串前面的“r”很重要——它表示该字符串是一个原始字符串，不能将反斜杠视为python转义符。matplotlib 有一个内置的 TeX 表达式解析器和布局引擎，并提供自己的数学字体。不需要安装 TeX 就可以跨平台使文本的数学表示而无需安装TeX。对于安装了 LaTeX 和 dvipng 的用户，还可以使用LaTeX格式化文本，并将输出直接合并到图的显示或保存到附件中。

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    4. mu, sigma = 100, 15
    5. x = mu + sigma * np.random.randn(10000)
    6. # 数据的直方图呈现
    7. n, bins, patches = plt.hist(x, 50, density=1, facecolor='g', alpha=0.75)
    8. # facecolor='g' 前景色为绿色
    9. # alpha=0.75 透明度 75%
    10. plt.xlabel('Smarts')            # x 标签
    11. plt.ylabel('Probability')       # y标签
    12. plt.title('Histogram of IQ')    # 标题
    13. plt.text(60, .025, r'$\mu=100,\ \sigma=15$')  # 60, .025为文本位置，后面为文本内容，r'$\mu=100,\ \sigma=15$'转数学表示法显示
    14. plt.axis([40, 160, 0, 0.03])    # y 轴刻度
    15. plt.grid(True)
    16. plt.show()

    image.png
    注释文本：
    ~matplotlib.pyplot.text 命令的用法是将注释文本放在轴上的任意位置。注释文本的一个常见用法是对绘图的某些功能进行注释，而 ~matplotlib.pyplot.annotate 方法为此提供了帮助，使注释变得更容易。在注释中，需要考虑两点：被注释的位置由参数“xy”和文本“xy text”的位置确定。这两个参数都是（x，y）元组。

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    4. ax = plt.subplot(111)
    6. t = np.arange(0.0, 5.0, 0.01)   # 产生0-5，步长为0.01的数组
    7. s = np.cos(2*np.pi*t)           # 计算其对应的 cos函数值
    8. #line, = plt.plot(t, s, lw=2)    # line,何用？后续代码未用到
    9. plt.plot(t, s, lw=2)            # 绘制曲线
    10. plt.annotate('local max', xy=(2, 1), xytext=(3, 1.5),
    11.              arrowprops=dict(facecolor='black', shrink=0.05),
    12.              )
    13. # xy=(2, 1), 注释点的位置
    14. # xytext=(3, 1.5) 注释文字的位置
    15. plt.ylim(-2, 2)
    16. plt.show()

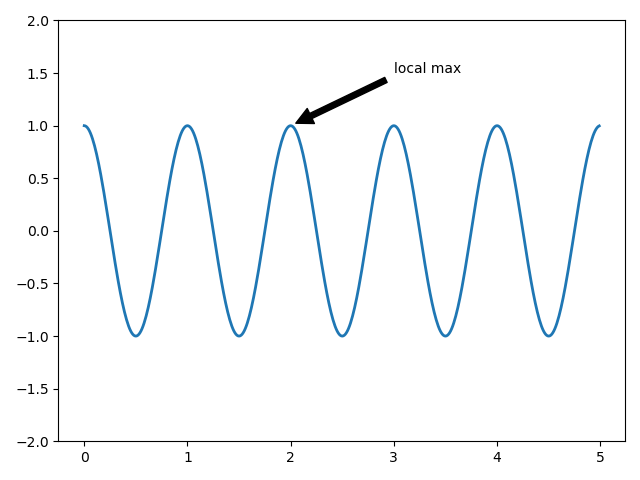
    image.png
    在这个基本示例中，“xy”（箭头尖）和“xy text”（文本位置）都使用了数据坐标，matplotlib 可以选择多种其他坐标系，用法参考文档。
    对数轴和其他非线性轴
    “matplotlib.pyplot”不仅支持线性轴刻度，还支持对数和对数刻度。当数据跨越许多数量级时通常使用此选项。更改轴的比例使用以下方法：

    1. plt.xscale（'log'）

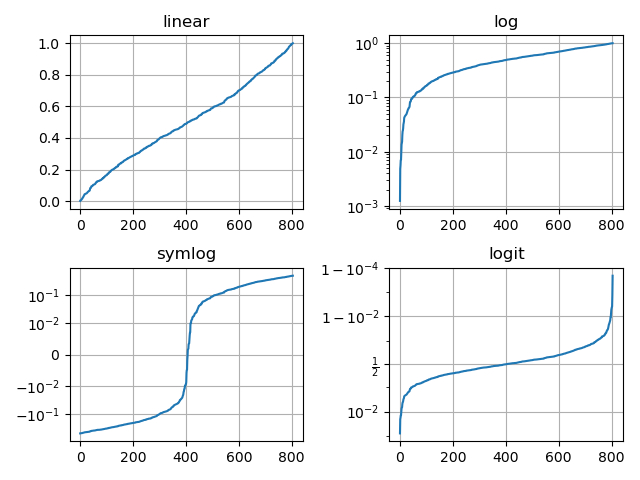
    下面例子里 y 轴具有相同数据，但使用不同比例的四个绘图示例：
    先独立绘图

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    5. np.random.seed(19730516) # 固定随机数种子
    7. # np.random.normal(loc=0,scale=1e-2,size=shape) ，产生正态分布：
    8. # 参数loc(float)：正态分布的均值，对应着这个分布的中心。loc=0说明这一个以Y轴为对称轴的正态分布，
    9. # 参数scale(float)：正态分布的标准差，对应分布的宽度，scale越大，正态分布的曲线越矮胖，scale越小，曲线越高瘦。
    10. # 参数size(int 或者整数元组)：输出的值赋在shape里，默认为None。
    12. # 产生（0，1）开区间的正态分布，正态分布均值0.5，标准差0.4，1000个值
    13. y = np.random.normal(loc=0.5, scale=0.4, size=1000)
    14. y = y[(y > 0) & (y < 1)]
    15. y.sort()
    16. x = np.arange(len(y))
    18. # 线性 linear
    19. plt.plot(x, y)
    20. plt.yscale('linear')
    21. plt.title('linear')
    22. plt.grid(True)
    23. plt.show()

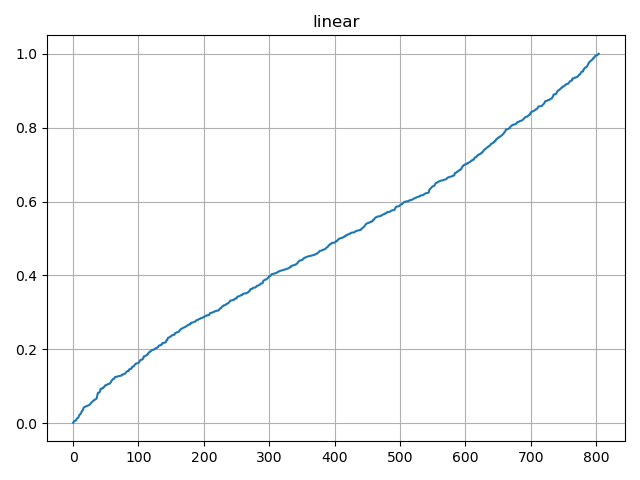
    image.png

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    5. np.random.seed(19730516) # 固定随机数种子
    6. # 产生（0，1）开区间的正态分布，正态分布均值0.5，标准差0.4，1000个值
    7. y = np.random.normal(loc=0.5, scale=0.4, size=1000)
    8. y = y[(y > 0) & (y < 1)]
    9. y.sort()
    10. x = np.arange(len(y))
    12. # 对数 log
    13. plt.plot(x, y)
    14. plt.yscale('log')
    15. plt.title('log')
    16. plt.grid(True)
    17. plt.show()

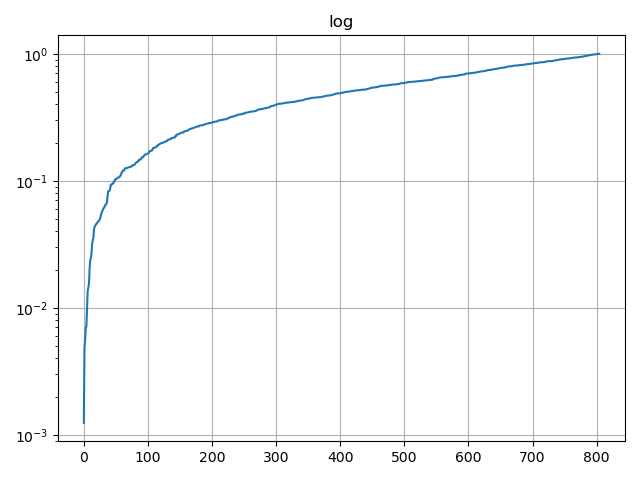
    image.png

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    5. np.random.seed(19730516) # 固定随机数种子
    6. # 产生（0，1）开区间的正态分布，正态分布均值0.5，标准差0.4，1000个值
    7. y = np.random.normal(loc=0.5, scale=0.4, size=1000)
    8. y = y[(y > 0) & (y < 1)]
    9. y.sort()
    10. x = np.arange(len(y))
    12. # 对称对数 symmetric log
    13. plt.plot(x, y - y.mean())
    14. plt.yscale('symlog', linthreshy=0.01)
    15. plt.title('symlog')
    16. plt.grid(True)
    17. plt.show()

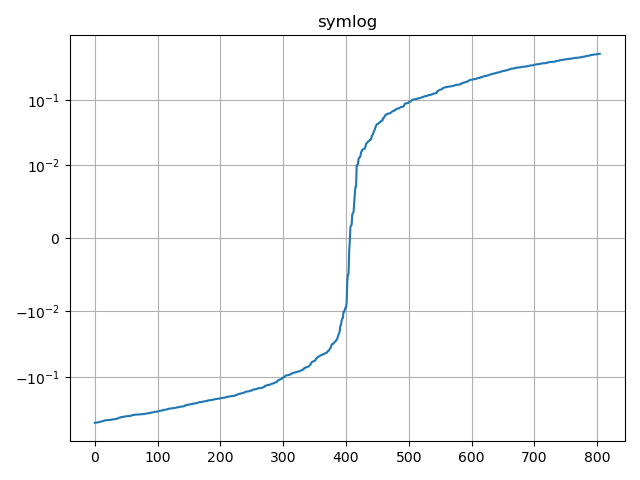
    image.png

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    5. np.random.seed(19730516) # 固定随机数种子
    6. # 产生（0，1）开区间的正态分布，正态分布均值0.5，标准差0.4，1000个值
    7. y = np.random.normal(loc=0.5, scale=0.4, size=1000)
    8. y = y[(y > 0) & (y < 1)]
    9. y.sort()
    10. x = np.arange(len(y))
    12. # logit
    13. plt.plot(x, y)
    14. plt.yscale('logit')
    15. plt.title('logit')
    16. plt.grid(True)
    17. plt.show()

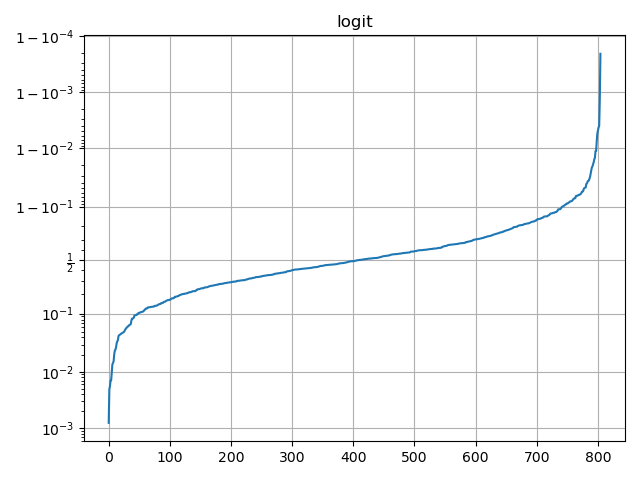
    image.png
    可以将这四幅图绘制在一个画布上：

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    5. np.random.seed(19730516) # 固定随机数种子
    7. # np.random.normal(loc=0,scale=1e-2,size=shape) ，产生正态分布：
    8. # 参数loc(float)：正态分布的均值，对应着这个分布的中心。loc=0说明这一个以Y轴为对称轴的正态分布，
    9. # 参数scale(float)：正态分布的标准差，对应分布的宽度，scale越大，正态分布的曲线越矮胖，scale越小，曲线越高瘦。
    10. # 参数size(int 或者整数元组)：输出的值赋在shape里，默认为None。
    12. # 产生（0，1）开区间的正态分布，正态分布均值0.5，标准差0.4，1000个值
    13. y = np.random.normal(loc=0.5, scale=0.4, size=1000)
    14. y = y[(y > 0) & (y < 1)]
    15. y.sort()
    16. x = np.arange(len(y))
    18. # plot with various axes scales
    19. plt.figure()
    21. # 线性 linear
    22. plt.subplot(221)
    23. plt.plot(x, y)
    24. plt.yscale('linear')
    25. plt.title('linear')
    26. plt.grid(True)
    29. # 对数 log
    30. plt.subplot(222)
    31. plt.plot(x, y)
    32. plt.yscale('log')
    33. plt.title('log')
    34. plt.grid(True)
    37. # 对称对数 symmetric log
    38. plt.subplot(223)
    39. plt.plot(x, y - y.mean())
    40. plt.yscale('symlog', linthreshy=0.01)
    41. plt.title('symlog')
    42. plt.grid(True)
    44. # logit
    45. plt.subplot(224)
    46. plt.plot(x, y)
    47. plt.yscale('logit')
    48. plt.title('logit')
    49. plt.grid(True)
    50. # 调整子图分布，logit因 y 刻度标签类似 "1 - 10^{-3}"，所以需要更多空间
    51. # wspace, hspace：子图之间的横向间距、纵向间距分别与子图平均宽度、平均高度的比值。
    52. plt.subplots_adjust(top=0.92, bottom=0.08, left=0.10, right=0.95, hspace=0.25, wspace=0.35)
    54. plt.show()

    image.png