绘制分形图

from math import sin, cos, pi
import matplotlib.pyplot as pl
from matplotlib import collections
class L_System(object):
    def __init__(self, rule):
        info = rule['S']
        for i in range(rule['iter']):
            ninfo = []
            for c in info:
                if c in rule:
                    ninfo.append(rule[c])
                else:
                    ninfo.append(c)
            info = "".join(ninfo)
        self.rule = rule
        self.info = info
    def get_lines(self):
        d = self.rule['direct']
        a = self.rule['angle']
        p = (0.0, 0.0)
        l = 1.0
        lines = []
        stack = []
        for c in self.info:
            if c in "Ff":
                r = d * pi / 180
                t = p[0] + l * cos(r), p[1] + l * sin(r)
                lines.append(((p[0], p[1]), (t[0], t[1])))
                p = t
            elif c == "+":
                d += a
            elif c == "-":
                d -= a
            elif c == "[":
                stack.append((p, d))
            elif c == "]":
                p, d = stack[-1]
                del stack[-1]
        return lines
rules = [
    {
        "F": "F+F--F+F", "S": "F",
        "direct": 180,
        "angle": 60,
        "iter": 8,
        "title": "Koch"
    },
    {
        "X": "X+YF+", "Y": "-FX-Y", "S": "FX",
        "direct": 0,
        "angle": 90,
        "iter": 13,
        "title": "Dragon"
    },
    {
        "f": "F-f-F", "F": "f+F+f", "S": "f",
        "direct": 0,
        "angle": 60,
        "iter": 7,
        "title": "Triangle"
    },
    {
        "X": "F-[[X]+X]+F[+FX]-X", "F": "FF", "S": "X",
        "direct": -45,
        "angle": 25,
        "iter": 8,
        "title": "Plant"
    },
    {
        "S": "X", "X": "-YF+XFX+FY-", "Y": "+XF-YFY-FX+",
        "direct": 0,
        "angle": 90,
        "iter": 6,
        "title": "Hilbert"
    },
    {
        "S": "L--F--L--F", "L": "+R-F-R+", "R": "-L+F+L-",
        "direct": 0,
        "angle": 45,
        "iter": 10,
        "title": "Sierpinski"
    },
]
def draw(ax, rule, iter=None):
    if iter != None:
        rule["iter"] = iter
    lines = L_System(rule).get_lines()
    linecollections = collections.LineCollection(lines)
    ax.add_collection(linecollections, autolim=True)
    ax.axis("equal")
    ax.set_axis_off()
    ax.set_xlim(ax.dataLim.xmin, ax.dataLim.xmax)
    ax.invert_yaxis()
fig = pl.figure(figsize=(7, 4.5))
fig.patch.set_facecolor("papayawhip")
for i in range(6):
    ax = fig.add_subplot(231 + i)
    draw(ax, rules[i])
help(ax.add_collection)
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, wspace=0, hspace=0)
pl.show()

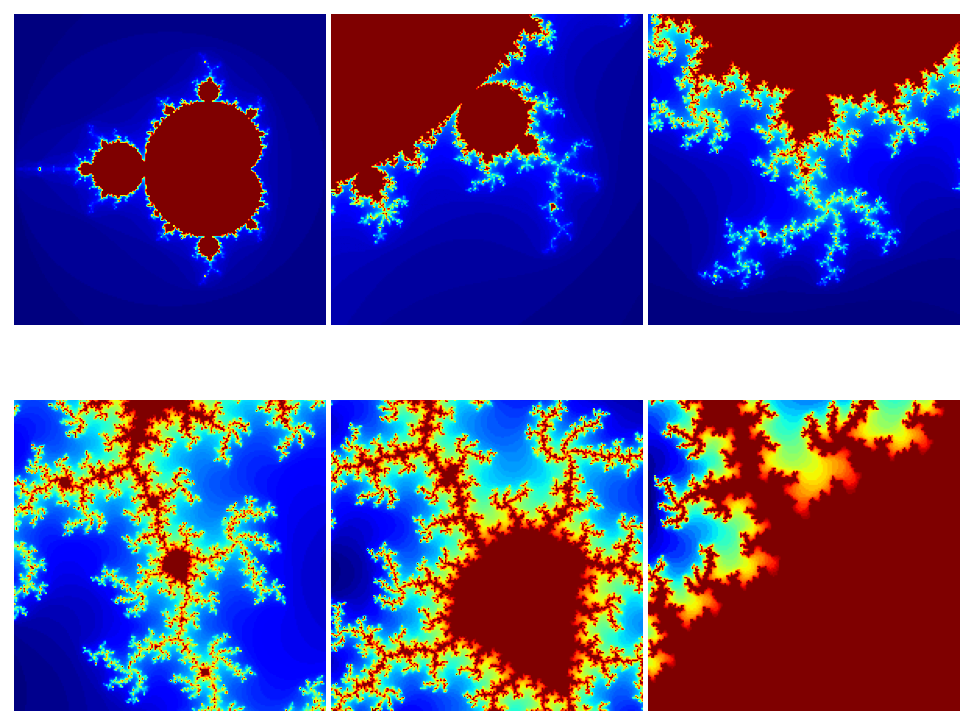
import numpy as np
import pylab as pl
from matplotlib import cm
def iter_point(c):
    z = c
    for i in range(1, 100):  # 最多迭代100次
        if abs(z) > 2:
            break  # 半径大于2则认为逃逸
        z = z * z + c
    return i  # 返回迭代次数
def draw_mandelbrot(cx, cy, d):
    """    绘制点(cx, cy)附近正负d的范围的Mandelbrot    """
    x0, x1, y0, y1 = cx - d, cx + d, cy - d, cy + d
    y, x = np.ogrid[y0:y1:200j, x0:x1:200j]
    c = x + y * 1j
    mandelbrot = np.frompyfunc(iter_point, 1, 1)(c).astype(np.float)
    pl.imshow(mandelbrot, cmap=cm.jet, extent=[x0, x1, y0, y1])
    pl.gca().set_axis_off()
x, y = 0.27322626, 0.595153338
pl.subplot(231)
draw_mandelbrot(-0.5, 0, 1.5)
for i in range(2, 7):
    pl.subplot(230 + i)
    draw_mandelbrot(x, y, 0.2 ** (i - 1))
    pl.subplots_adjust(0.02, 0, 0.98, 1, 0.02, 0)
pl.show()