蒙特卡洛(Monte Carlo)方法是由数学家冯·诺伊曼提出的,诞生于上世纪40年代美国的“曼哈顿计划”。蒙特卡洛是一个地名,位于赌城摩纳哥,象征概率。蒙特卡洛方法的原理是通过大量随机样本,去了解一个系统,进而得到所要计算的值。
1. 计算圆周率
用蒙特卡洛方法计算圆周率π的原理如下:一个边长为2r的正方形内部相切一个半径为r的圆,圆的面积是πr2,正方形的面积为4r2,二者面积之比是π/4,因为比值与r大小无关,所以可以假设半径 r的值为1。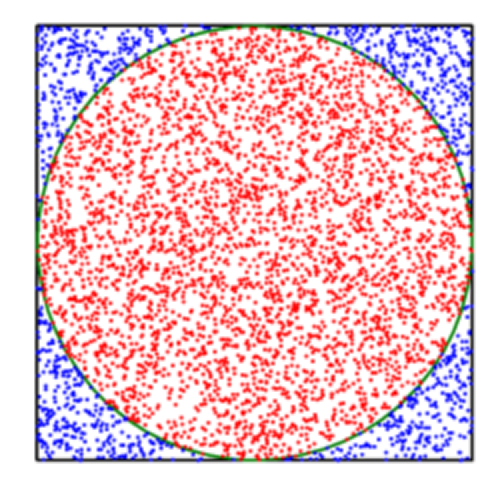
在这个正方形内部,随机产生n个点,坐标为(x,y),当随机点较多时,可以认为这些点服从均匀分布的规律。计算每个点与中心点的距离是否大于圆的半径(x2+y2>r2),以此判断是否落在圆的内部。统计圆内的点数c,c与n的比值乘以4,就是π的值。理论上,n越大,计算的π值越准,但由于随机数不能保证完全均匀分布,所以蒙特卡洛法每次计算结果可能不同。
编程实现用蒙特卡洛方法计算π值,为了自动测评的需要,请先读入一个正整数sd作为随机数种子,并要求使用 x,y = random.uniform(-1,1) , random.uniform(-1,1) 语句来生成随机点的坐标值。
import randomdef monte_carlo_pi(num):"""接收正整数为参数,表示随机点的数量,利用蒙特卡洛方法计算圆周率返回值为表示圆周率的浮点数"""hits = 0 #计数器,落在圆内的点数,初值为0for i in range(num): #x,y = random.uniform(-1,1),random.uniform(-1,1)if x**2 + y**2 < 1 :# 计算坐标(x,y)到原点的距离,小于半径则在圆内hits += 1pi =(hits / num) * 4return piif __name__ == '__main__':sd = int(input()) #读入随机数种子random.seed(sd) #设置随机数种子times = int(input()) # 输入正整数,表示产生点数量print(monte_carlo_pi(times)) # 输出圆周率值,浮点数
2. Tutle演示计算圆周率
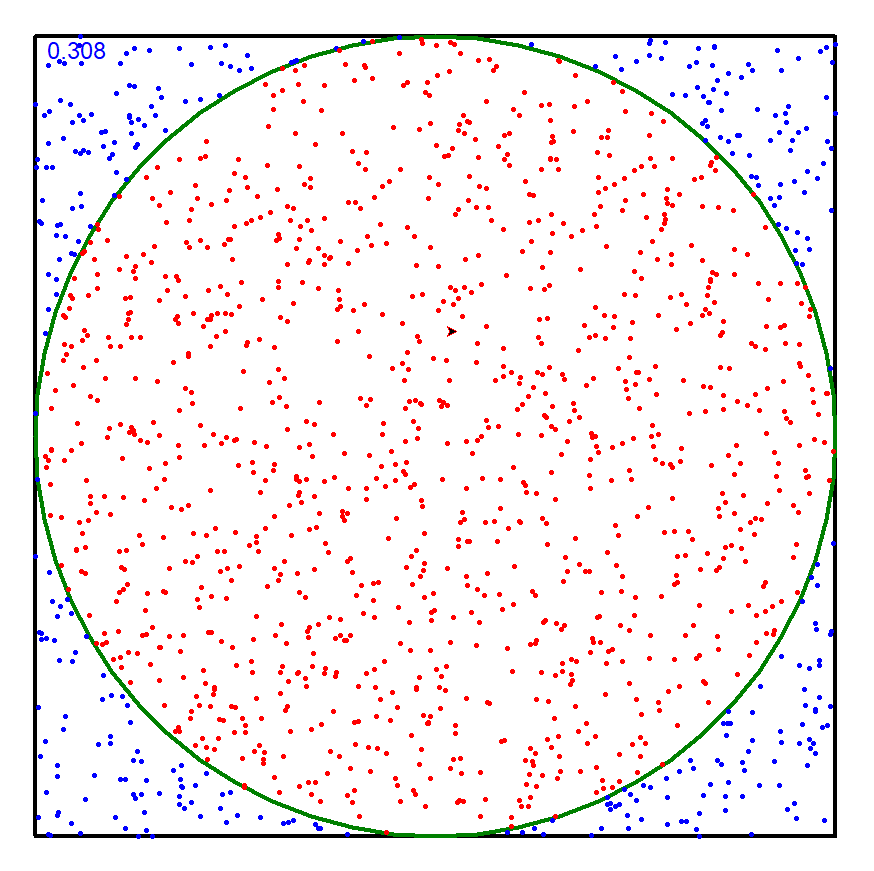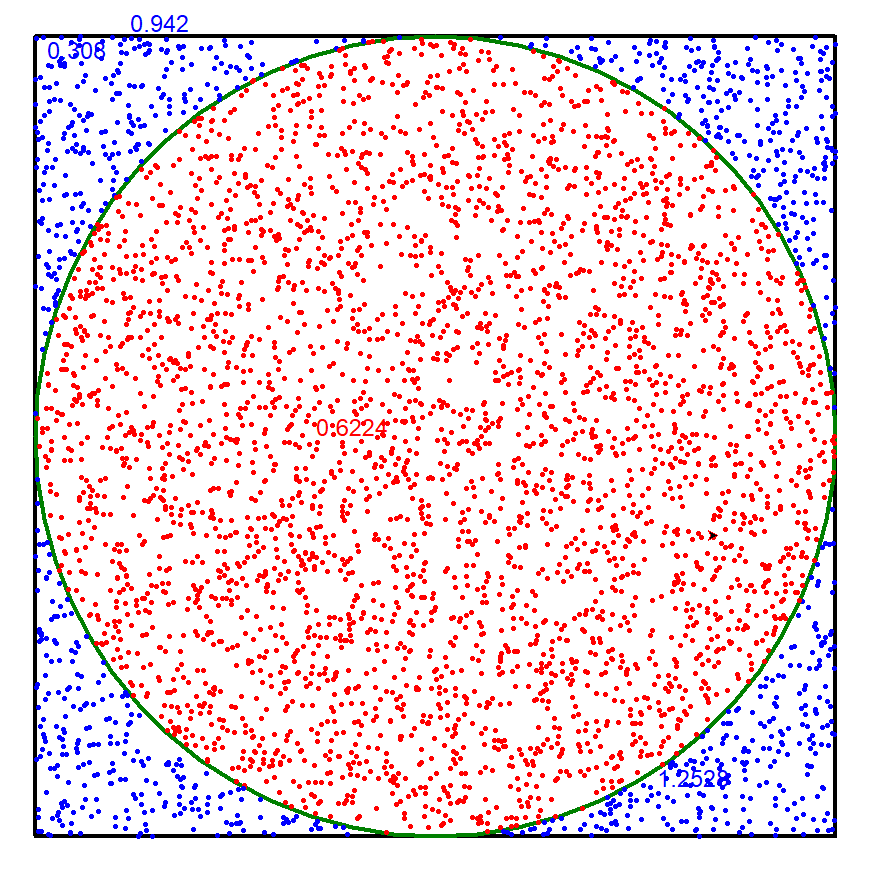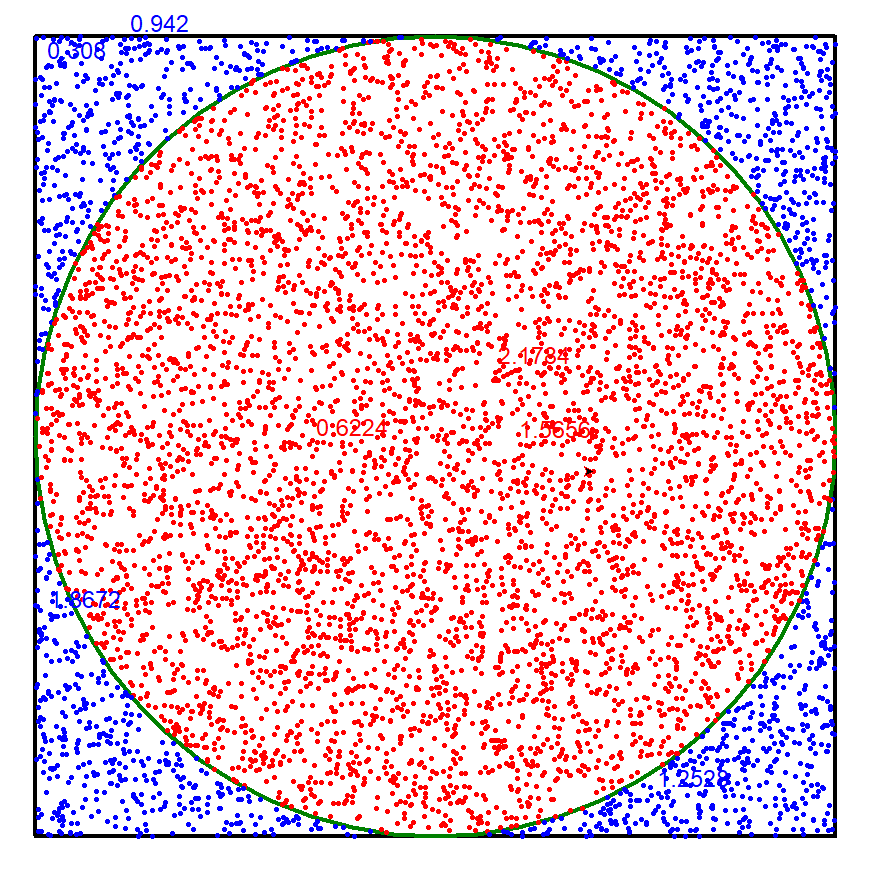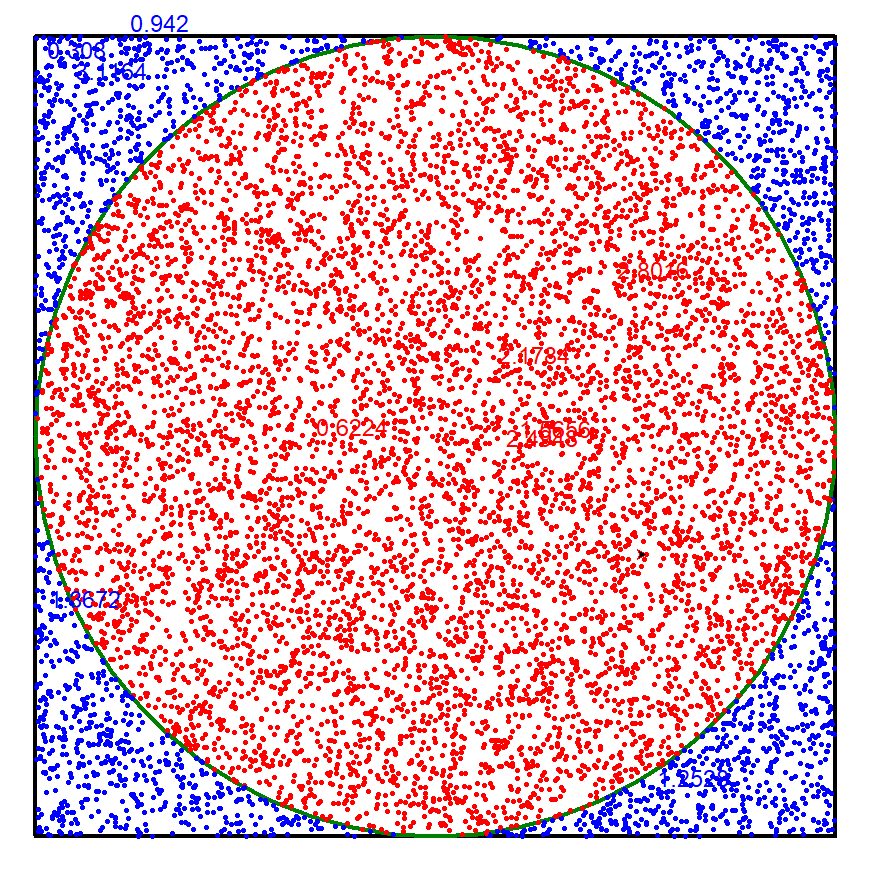
import randomimport turtles,n = map(int,input().split())random.seed(s)hits = 0turtle.tracer(1000) #刷新间隔turtle.update() #刷新turtle.pensize(4)turtle.penup()turtle.goto(-400, -400)turtle.pendown()for i in range(4):turtle.forward(800)turtle.left(90)turtle.forward(400)turtle.pencolor('green')turtle.circle(400)for i in range(1, n+1):x, y = random.random(), random.random()signx,signy = random.choice('+-'),random.choice('+-')pos = (x ** 2 + y ** 2)**0.5if pos <= 1.0:hits = hits + 1turtle.pencolor('red')else:turtle.pencolor('blue')x = float(signx+str(x))y = float(signy+str(y))turtle.penup()turtle.goto(x * 400, y * 400)turtle.pendown()turtle.dot(5)pi = 4 * (hits / n)if i%1000 ==0:turtle.write(pi, font=("Arial", 18, "normal"))pi = 4 * (hits/n)print("Pi值是{}。".format(pi))turtle.hideturtle()turtle.done()
3. matplotlib演示计算圆周率
# ------------ ------- -------- ----------- -----------# @File : 4.4.4 计算圆周率.py# @Contact : vasp@qq.com# @Copyright : 2018-2025, Wuhan University of Technology# @Modify Time: 2021/4/26 23:22# @Author : 赵广辉# @Version : 1.0# @License : 仅限用于Python程序设计基础实践教程(赵广辉,高等教育出版社)配套实验# ------------ ------- -------- ----------- -----------# 本题中增加了用Matplotlib和 turtle演示蒙特卡洛的函数,可以考虑给学生运行查看演示# 增加了'梅钦法'和'拉马努金法'计算圆周率,可以考虑给学生# 函数文档中增加了测试,在Pycharm中运行时需要点if __name__ == '__main__':旁边的绿三角符号,再运行当前文件名# 也可以先删除文档注释中的测试用例,给学生的模板中我没有加,如果有老师需要,可以加上测试部分。import mathimport randomimport matplotlib.pyplot as pltimport numpy as npimport turtledef monte_carlo_pi(num, s):"""接收一个表示随机次数的整数和一个整数做随机数种子,用蒙特卡洛法计算圆周率。当产生点的坐标(x,y)落在圆内时执行in_circle_lst.append((x, y))将坐标加入到列表in_circle_lst,产生点的坐标(x,y)落在圆外部时执行out_circle_lst.append((x, y))将坐标加入到列表out_circle_lst,以浮点数形式返回圆周率值。"""random.seed(s)hits = 0 # 落在圆内的计数器初值设为 0for i in range(1, num + 1):x, y = random.uniform(-1, 1), random.uniform(-1, 1) # 生成两个随机数模拟一个点的坐标pos = (x ** 2 + y ** 2) ** 0.5 # 计算坐标(x,y)到原点的距离if pos <= 1.0: # 如果距离小于等于1,点在圆内hits = hits + 1in_circle_lst.append((x, y))else:out_circle_lst.append((x, y))pi = 4 * (hits / num)monte_carlo_show(in_circle_lst, out_circle_lst) # 调用函数可演示蒙特卡洛估计圆周率值monte_carlo_pi_turtle(num, s)return pidef monte_carlo_show(in_circle_lst, out_circle_lst):"""@参数 in_circle_lst:落在圆内的点的坐标列表@参数 out_circle_lst:落在圆外的点的坐标列表"""plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号plt.figure(figsize=(11, 11)) # 设置画布长宽x_in_circle = [x[0] for x in in_circle_lst] # 落在圆内的点的列表xy_in_circle = [x[1] for x in in_circle_lst] # 落在圆内的点的列表yx_out_circle = [x[0] for x in out_circle_lst] # 落在圆外的点的列表xy_out_circle = [x[1] for x in out_circle_lst] # 落在圆外的点的列表yplt.scatter(x_out_circle, y_out_circle, s=10, facecolors='blue') # 绘制散点,落在圆外在点颜色用蓝色plt.scatter(x_in_circle, y_in_circle, s=5, facecolors='red') # 绘制散点,落在圆内在点颜色用红色plt.title('蒙特卡洛法计算圆周率演示') # 图的标题plt.show() # 显示绘制结果# 给出turtle模板,学生填monte_carlo代码,帮助学生理解算法,了解turtle绘图def monte_carlo_pi_turtle(n, s):"""用turtle绘图模拟蒙特卡洛n次结果"""random.seed(s)turtle.tracer(1000)turtle.pensize(4)turtle.penup()turtle.goto(-300, -300)turtle.pendown()for i in range(4):turtle.forward(600)turtle.left(90)turtle.forward(300)turtle.pencolor('green')turtle.circle(300)hits = 0 # 落在圆内的计数器初值设为 0for i in range(1, n + 1):x, y = random.uniform(-1, 1), random.uniform(-1, 1) # 生成两个随机数模拟一个点的坐标pos = (x ** 2 + y ** 2) ** 0.5 # 计算坐标(x,y)到原点的距离if pos <= 1.0: # 如果距离小于等于1,点在圆内hits = hits + 1turtle.pencolor('red') # 落在圆内在点颜色用红色else: # 如果距离大于1,点在圆外turtle.pencolor('blue') # 落在圆内在点颜色用蓝色turtle.penup()turtle.goto(x * 300, y * 300) # 画笔抬起并移动到数值放大400倍的x,y处turtle.pendown()turtle.dot(3) # 画一个半径为 3 的圆点if i % 10000 == 0: # 实验为10000的倍数次时turtle.pencolor('black')pi = 4 * (hits / i) # 根据落在圆内外的点数量估算PI值turtle.penup() # 画笔抬起turtle.goto(320, 150 - i // 1000 * 30) # 移动到区域外记录当前PI值turtle.pendown() # 画笔抬起turtle.write("{}次时PI的值是{:.4f}".format(i, pi), font=("宋体", 18, "normal"))turtle.hideturtle() # 隐藏光标turtle.update() # 刷新turtle.done() # 结束绘制if __name__ == '__main__':num = int(input()) # 输入模拟次数in_circle_lst, out_circle_lst = [], []print(monte_carlo_pi(num, 1973)) # 输出函数运行结果
4.模拟股票价格
在金融工程中,有下面这样一个公式,他利用目前的股价 去预测
时间之后的股价
:
这其中的参数我来解释一下: 表示股票收益率的期望值,这里我们设定为
,即
表示股票的波动率,这里设定为
,其中
表示整数年份,
表示在整个估算周期内,取的具体步数,就好比说
为一年,
如果取244,那么
的粒度就是每个交易日了(一年有244个交易日)。
这里面似乎所有的参数都是确定的,唯独除了 之外,
是一个服从标准正态分布的随机变量,这是这个
,决定了每日的股价
是一个随机变量,而由股价构成的序列是一个随机过程。
我们同样的用蒙特卡罗方法,利用大样本来估计一下在目前股价为 的情况下,1年之后股价的概率分布情况。
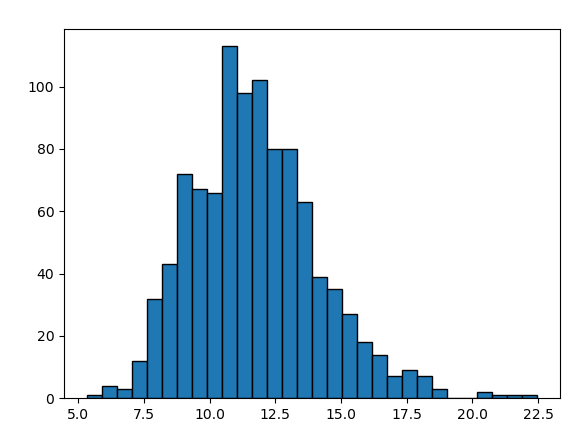
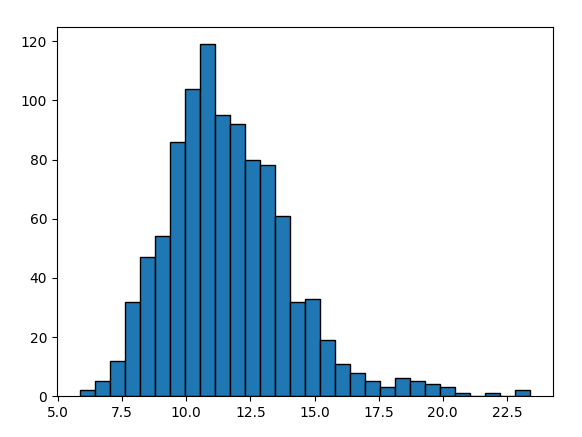
这是我们模拟了10000个样本经过上述随机过程,在一年之后股价的分布情况。
这里的核心就是:
e = numpy.random.randn() s = s+musdt+sigmasemath.sqrt(dt)
每一轮 ,我们都生成一个服从标准正态分布的随机变量
,不断通过递推公式
,迭代出下一个时间点的股价,循环往复直到生成一年后的最终结果,这样就模拟出了一年过程中股价随机变量序列构成的随机过程。
我们采用蒙特卡罗方法,设置大样本量(这里设置10000个),最终迭代出10000个对应的一年后股价,然后用柱状图就能看出其总体分布特征。
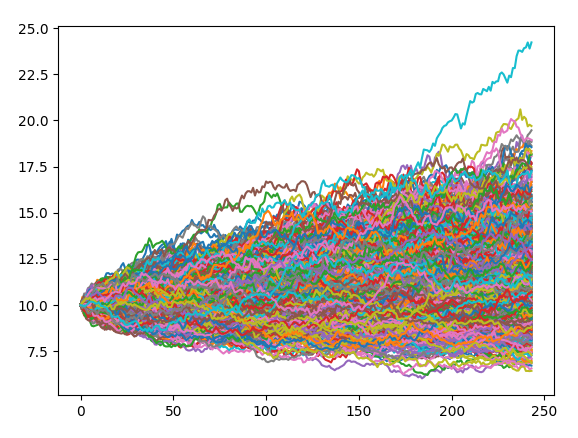
*股价变化曲线的过程展现
上面我们分析的是这10000个样本在一年之后最终股价的整体分布情况,实际上我们还有一个同样重要的过程可以进行监测和展现,那就是从 时刻起到1年后的这一段时间内,每隔
时间间隔点由实时价格随机变量构成的序列,换句话说就是随机过程的整体展现。这个在上面的基础上进一步完成,其实不难,就是我们不光要计算出股票最终的价格,还有记录下每个
时间点的价格,并把他记录下来。
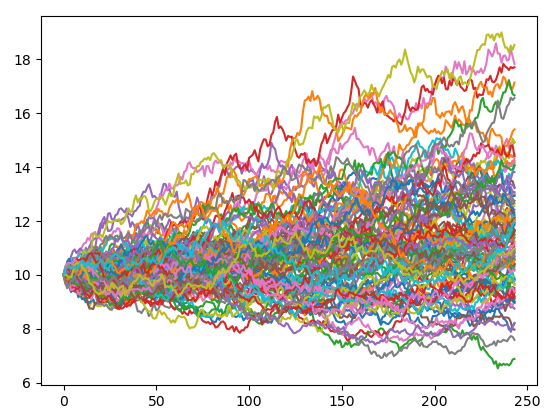
这里我们清晰的展现出了由244个 时间点的股价数据所构成的序列,这是随着时间变化的随机过程。我们为了从整体把握他的分布特征,设定了100个样本,因此模拟出了100条价格曲线。
这种结果图表面上看起来比较凌乱,实际上可以从整体上发现许多端倪,例如股价在运行过程中的整体分布区间,上下界,集中程度等等,都可以有一个整体的把握。
因此我们不仅可以得到最终股价的分布,也可以知道股价运行变化的完整价格路径,这个价格路径代表了蒙特卡罗方法的精髓,通过这个价格路径的可视化呈现,让我们更加直观的从宏观上把握了随机过程。
import mathimport numpy as npimport matplotlib.pyplot as plts0 = 10.0T = 1.0n = 244 * Tmu = 0.15sigma = 0.2n_simulation = 1000dt = T / ns_array = []for i in range(n_simulation):s = s0for j in range(int(n)):e = np.random.randn()# e = scipy.random.normal()s = s + mu * s * dt + sigma * s * e * math.sqrt(dt)s_array.append(s)plt.hist(s_array, bins=30, edgecolor='k')plt.show()dt = T / nrandom_series = np.zeros(int(n), dtype=float)x = range(0, int(n))for i in range(n_simulation):random_series[0] = s0for j in range(1, int(n)):e = np.random.randn()# e = scipy.random.normal()random_series[j] = random_series[j - 1] + mu * random_series[j - 1] * dt + sigma * random_series[j - 1] * e * math.sqrt(dt)plt.plot(x, random_series)plt.show()