根据数组构造二叉树

从中序与后序遍历序列构造二叉树

题目描述

力扣链接🔗

题目分析

大体思路是根据后序遍历的最后一个节点可以知道根节点，然后再通过根节点先切割中序数组，中序遍历中切割数组，此时根节点的左侧就是左孩子的中序数组，根节点的右侧就是右孩子的中序数组。（先切割中序数组的原因是后序数组的切割需要中序数组来作为判断）然后再根据中序数组切割后序数组，再进行递归。

代码分析

步骤：

• 第一步：如果数组大小为零的话，说明是空节点了。
• 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
• 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
• 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
• 第五步：切割后序数组，切成后序左数组和后序右数组
• 第六步：递归处理左区间和右区间

注意：再切割的过程中统一使用的是左闭右开的区间进行分割。

后序数组的切割的话需要根据中序数组左右子树数组的长度进行切割。就是中序数组大小一定是和后序数组的大小相同的（这是必然）。

中序数组我们都切成了左中序数组和右中序数组了，那么后序数组就可以按照左中序数组的大小来切割，切成左后序数组和右后序数组。

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return traversal(inorder, 0, inorder.length, postorder, 0, postorder.length);
    }
    /**
     * @param inorder   中序数组
     * @param inLeft    中序左孩子数组
     * @param inRight   中序右孩子数组
     * @param postorder 后序数组
     * @param postLeft  后序左孩子数组
     * @param postRight 后序右孩子数组
     * @return
     */
    public TreeNode traversal(
            int[] inorder, int inLeft, int inRight,
            int[] postorder, int postLeft, int postRight
    ) {
        // 第一步：如果数组大小为零的话，说明是空节点了。
        if (inRight - inLeft < 1) {
            return null;
        }
        // 只有一个元素也直接返回
        if (inRight - inLeft == 1) {
            return new TreeNode(inorder[inLeft]);
        }
        // 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
        int rootValue = postorder[postRight - 1];
        // 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
        int rootIndex = 0;
        for (int i = inLeft; i < inRight; i++) {    // 注意停止条件不能为 inorder.length - 1，会变化
            if (inorder[i] == rootValue) {
                rootIndex = i;
                break;
            }
        }
        // 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
        // 第五步：切割后序数组，切成后序左数组和后序右数组
        // 第六步：递归处理左区间和右区间
        TreeNode root = new TreeNode(rootValue);    // 生成节点
        // 统一采用左闭右开切割
        root.left = traversal(inorder, inLeft, rootIndex,
                postorder, postLeft, postLeft + (rootIndex - inLeft));
        root.right = traversal(inorder, rootIndex + 1, inRight,
                postorder, postLeft + (rootIndex - inLeft), postRight - 1);
        return root;
    }
}

从前序与中序遍历序列构造二叉树

题目描述

力扣链接🔗

代码分析

思路和上题一致，注意区间分割还是按照左闭右开的区间进行分割。

class ConstructBinaryTreeFromPreorderAndInorderTraversal {
    public static void main(String[] args) {
        Solution solution = new ConstructBinaryTreeFromPreorderAndInorderTraversal().new Solution();
    }
    //leetcode submit region begin(Prohibit modification and deletion)
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {
        }
        TreeNode(int val) {
            this.val = val;
        }
        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }
    class Solution {
        public TreeNode buildTree(int[] preorder, int[] inorder) {
            return traversal(inorder, 0, inorder.length, preorder, 0, preorder.length);
        }
        /**
         * @param inorder  中序数组
         * @param inLeft   中序左孩子数组
         * @param inRight  中序右孩子数字
         * @param preorder 前序数组
         * @param preLeft  前序左孩子数组
         * @param preRight 前序右孩子数组
         * @return
         */
        public TreeNode traversal(
                int[] inorder, int inLeft, int inRight,
                int[] preorder, int preLeft, int preRight
        ) {
            if (preRight - preLeft < 1) {
                return null;
            }
            if (preRight - preLeft == 1) {
                return new Tre    eNode(preorder[preLeft]);
            }
            // 找出根节点
            int rootValue = preorder[preLeft];
            int rootIndex = 0;
            for (int i = inLeft; i <= inRight; i++) {
                if (inorder[i] == rootValue) {
                    rootIndex = i;
                    break;
                }
            }
            TreeNode root = new TreeNode(rootValue);
            // 统一按照左闭右开切割
            root.left = traversal(
                    inorder, inLeft, rootIndex,
                    preorder, preLeft + 1, preLeft + (rootIndex - inLeft) + 1
            );
            root.right = traversal(
                    inorder, rootIndex + 1, inRight,
                    preorder, preLeft + (rootIndex - inLeft) + 1, preRight
            );
            return root;
        }
    }

最大二叉树

题目描述

力扣链接🔗

题目思路

大体思路也是分割路径，先寻找最大的元素索引，在切割数组依次递归，大体模板和上面2题一致。

• 确定递归函数的参数和返回值
  参数就是传入的是存放元素的数组，返回该数组构造的二叉树的头结点，返回类型是指向节点的指针。
• 确定终止条件
  题目中说了输入的数组大小一定是大于等于1的，所以我们不用考虑小于1的情况，那么当递归遍历的时候，如果传入的数组大小为1，说明遍历到了叶子节点了。
  那么应该定义一个新的节点，并把这个数组的数值赋给新的节点，然后返回这个节点。 这表示一个数组大小是1的时候，构造了一个新的节点，并返回。
• 确定单层递归的逻辑
  单层逻辑：进行左右孩子数组的切割，使用左闭右开的原则进行切割。

代码

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return traversal(nums, 0, nums.length);
    }
    public TreeNode traversal(int[] nums, int left, int right) {
        if (right - left < 1) {
            return null;
        }
        if (right - left == 1) {
            return new TreeNode(nums[left]);
        }
        // 获取最大值的索引
        int maxIndex = left;
        for (int i = left + 1; i < right; i++) {    // 一定注意起始和结束范围不是0到数组最后一位
            if (nums[i] > nums[maxIndex]) {
                maxIndex = i;   // 不能加break，因为需要找到最大的值索引
            }
        }
        // 左闭右开的分割
        TreeNode root = new TreeNode(nums[maxIndex]);
        root.left = traversal(nums, left, maxIndex);
        root.right = traversal(nums, maxIndex + 1, right);
        return root;
    }
}

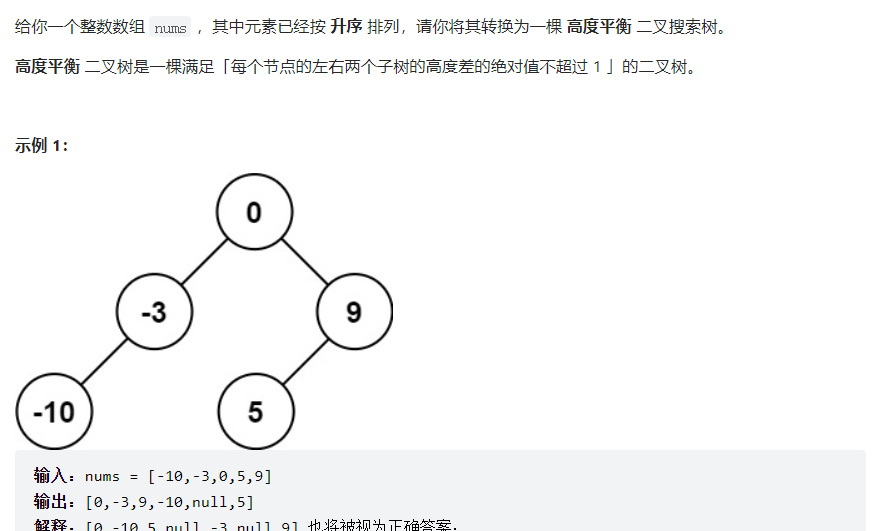
构建二叉搜索树

题目描述

🔗

解题思路

可知数组已按升序排列，那么构建二叉搜索树应该从中间的数字开始狗仔为一棵平衡树（也可以不构造平衡树，但何必为难自己）

递归构造方法模板修改即可

public TreeNode sortedArrayToBST(int[] nums) {
    if (nums.length == 0) {
        return null;
    }
    return traversal(nums, 0, nums.length);
}
public TreeNode traversal(int[] nums, int left, int right) {
    if (right - left == 1) {
        return null;
    }
    // 找到中间的节点
    int mid = (left + right) / 2;
    TreeNode root = new TreeNode(nums[mid]);
    // 递归构造
    root.left = traversal(nums, left, mid);
    root.right = traversal(nums, mid, right);
    return root;
}

迭代法

用三个队列分别存储节点和左右边界进行构造。

/**
        * 迭代法
        *
        * @param nums
        * @return
        */
public TreeNode sortedArrayToBST(int[] nums) {
    if (nums.length == 0) {
        return null;
    }
    Queue<Integer> leftQueue = new LinkedList<>();  // 左边界队列
    Queue<Integer> rightQueue = new LinkedList<>(); // 右边界队列
    Queue<TreeNode> nodeQueue = new LinkedList<>(); // 节点队列
    // 初始化队列，整体采用左闭右开划分数组
    TreeNode root = new TreeNode(0);
    leftQueue.offer(0);
    rightQueue.offer(nums.length - 1);
    nodeQueue.offer(root);
    while (!nodeQueue.isEmpty()) {
        TreeNode node = nodeQueue.poll();
        Integer left = leftQueue.poll();
        Integer right = rightQueue.poll();
        // 将数组mid值赋值给节点
        int mid = (left + right) / 2;
        node.val = nums[mid];
        // 处理左边节点
        if (left <= mid - 1) {
            node.left = new TreeNode(0);
            nodeQueue.offer(node.left);
            leftQueue.offer(left);
            rightQueue.offer(mid - 1);
        }
        // 处理右边节点
        if (right >= mid + 1) {
            node.right = new TreeNode(0);
            nodeQueue.offer(node.right);
            leftQueue.offer(mid + 1);
            rightQueue.offer(right);
        }
    }
    return root;
}