题目描述

解题思路

大体思路：就是使用一个复制栈来记录递减的数组。
普通栈的 push() 和 pop() 函数的复杂度为 O(1) ；而获取栈最小值 min() 函数需要遍历整个栈，复杂度为 O(N) 。

本题难点： 将 min() 函数复杂度降为 O(1) ，可通过建立辅助栈实现；
数据栈 A ： 栈 A 用于存储所有元素，保证入栈 push() 函数、出栈 pop() 函数、获取栈顶 top() 函数的正常逻辑。
辅助栈 B ： 栈 B 中存储栈 A 中所有 非严格降序 的元素，则栈 A 中的最小元素始终对应栈 B 的栈顶元素，即 min() 函数只需返回栈 B 的栈顶元素即可。
因此，只需设法维护好 栈 B 的元素，使其保持非严格降序，即可实现 min() 函数的 O(1) 复杂度。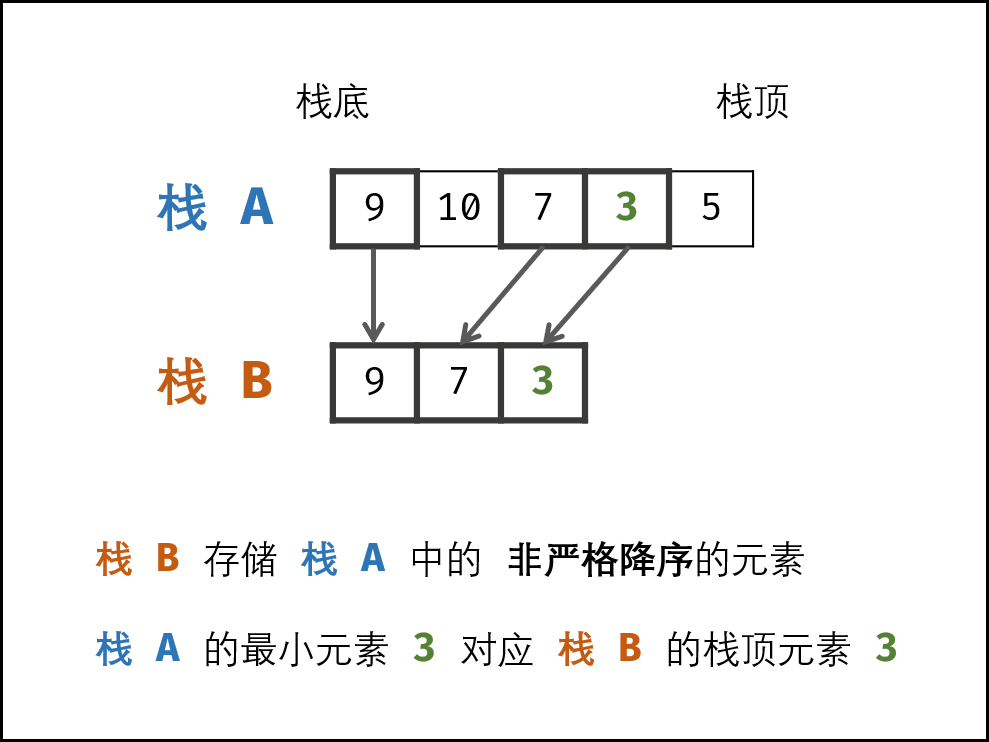

函数设计：

• push(x) 函数： 重点为保持栈 B 的元素是 非严格降序 的。
  • 将 x 压入栈 A （即 A.add(x) ）；
  • 若 ① 栈 B 为空 或 ② x 小于等于 栈 B 的栈顶元素，则将 x 压入栈 B （即 B.add(x) ）。
• pop() 函数： 重点为保持栈 A, B 的 元素一致性 。
  • 执行栈 A 出栈（即 A.pop() ），将出栈元素记为 y ；
  • 若 y 等于栈 B 的栈顶元素，则执行栈 B 出栈（即 B.pop() ）。
• top() 函数： 直接返回栈 A 的栈顶元素即可，即返回 A.peek() 。
• min() 函数： 直接返回栈 B 的栈顶元素即可，即返回 B.peek() 。

复杂度分析：
时间复杂度 O(1) ： push(), pop(), top(), min() 四个函数的时间复杂度均为常数级别。
空间复杂度 O(N) ： 当共有 N 个待入栈元素时，辅助栈 B 最差情况下存储 N 个元素，使用 O(N) 额外空间。

class MinStack {
    // 数据栈 A ： 栈 A 用于存储所有元素，保证入栈 push() 函数、出栈 pop() 函数、获取栈顶 top() 函数的正常逻辑。
    Stack<Integer> stack1;
    // 辅助栈 B ： 栈 B 中存储栈 A 中所有 非严格降序 的元素，则栈 AA中的最小元素始终对应栈 B 的栈顶元素，即 min() 函数只需返回栈 BB 的栈顶元素即可。
    Stack<Integer> stack2;
    /**
         * initialize your data structure here.
         */
    public MinStack() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }
    public void push(int x) {
        stack1.push(x);
        if (stack2.isEmpty()) {
            stack2.push(x);   // stack2为空，那么这个元素就是最小的
        } else {    // stack2不为空
            if (stack2.peek() >= x) stack2.push(x);  // 如果前面的数大于入栈的数，那么就直接入栈
        }
    }
    public void pop() {
        // 注意使用equals，在[-128,127]会存在缓存
        if (stack1.pop().equals(stack2.peek())) stack2.pop();    // 如果stack1出栈的元素和stack2栈顶相等，那么就一起出栈
    }
    public int top() {
        return stack1.peek();
    }
    public int min() {
        return stack2.peek();
    }
}