题目描述

image.png

解题思路

本问题是典型的矩阵搜索问题，可使用 深度优先搜索（DFS）+ 剪枝 解决。
深度优先搜索： 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
剪枝： 在搜索中，遇到 这条路不可能和目标字符串匹配成功 的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为 可行性剪枝 。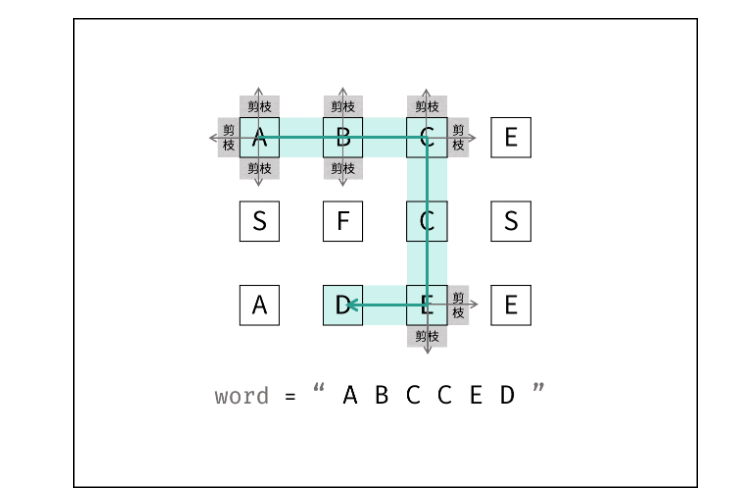
image.png
DFS 解析：

  • 递归参数： 当前元素在矩阵 board 中的行列索引 i 和 j ，当前目标字符在 word 中的索引 k 。
  • 终止条件：
    • 返回 false ： (1) 行或列索引越界 或 (2) 当前矩阵元素与目标字符不同 或 (3) 当前矩阵元素已访问过 （ (3) 可合并至 (2) ） 。
    • 返回 true ： k = len(word) - 1 ，即字符串 word 已全部匹配。
  • 递推工作：
    1. 标记当前矩阵元素： 将 board[i][j] 修改为 空字符 ‘’ ，代表此元素已访问过，防止之后搜索时重复访问。
    2. 搜索下一单元格： 朝当前元素的 上、下、左、右 四个方向开启下层递归，使用 或 连接 （代表只需找到一条可行路径就直接返回，不再做后续 DFS ），并记录结果至 res 。
    3. 还原当前矩阵元素： 将 board[i][j] 元素还原至初始值，即 word[k] 。
  • 返回值： 返回布尔量 res ，代表是否搜索到目标字符串。

本题大体思路就是最每个矩阵的元素进行DFS搜索，注意搜的时候题意要求是上下左右搜索，所以递归的时候是每个方向都需要递归，判断是否越界防止以及是否满足条件来停止递归。

  2. public boolean exist(char[][] board, String word) {
  3.     if (word == null && word.length() == 0) return true;
  4.     char[] wordArray = word.toCharArray();
  5.     // 每次字符都进行搜索
  6.     for (int i = 0; i < board.length; i++) {
  7.         for (int j = 0; j < board[0].length; j++) {
  8.             // 注意不能直接 return dfs(board, wordArray, i, j, 0);
  9.             // 此时这种情况只会搜索一次，而不是每个字符都搜索
  10.             // 所以会漏掉反序的情况
  11.             // [["a","b"]]
  12.             // "ba"
  13.             if (dfs(board, wordArray, i, j, 0)) return true;
  14.         }
  15.     }
  16.     return false;
  17. }
  20. /**
  21.          * 上下左右都要搜索
  22.          *
  23.          * @param board
  24.          * @param word
  25.          * @param row
  26.          * @param col
  27.          * @param index
  28.          * @return
  29.          */
  30. public boolean dfs(char[][] board, char[] word, int row, int col, int index) {
  31.     // 字符和word中不相等，以及左右上下超过board的范围，此时都是返回false
  32.     // board[row][col] != word[index]放在最后不然有数组越界问题，得先判断行和列的范围
  33.     if (row >= board.length || row < 0 || col >= board[0].length || col < 0 || board[row][col] != word[index])
  34.         return false;
  35.     // 此时搜索的索引等于word，此时搜索完毕
  36.     if (index == word.length - 1) return true;
  38.     board[row][col] = '\0'; // 表示此位置已经搜索过且满足，前面不满足的已经返回false
  39.     // 像下左右进行递归搜索，+1会自动回溯
  40.     boolean isEqual =
  41.         dfs(board, word, row + 1, col, index + 1)  // 搜索下边
  42.         || dfs(board, word, row - 1, col, index + 1)    // 搜索上边
  43.         || dfs(board, word, row, col + 1, index + 1)    // 搜索右边
  44.         || dfs(board, word, row, col - 1, index + 1); // 搜索左边
  45.     board[row][col] = word[index];  // 回溯，返回原来的字符
  46.     return isEqual;
  47. }
  48. }
  • 时间复杂度 O(3 K MN) ： 最差情况下，需要遍历矩阵中长度为 KK 字符串的所有方案，时间复杂度为 O(3 K )；矩阵中共有 MN 个起点，时间复杂度为 O(MN) 。方案数计算： 设字符串长度为 KK ，搜索中每个字符有上、下、左、右四个方向可以选择，舍弃回头（上个字符）的方向，剩下 3 种选择，因此方案数的复杂度为 O(3 K) 。
  • 空间复杂度 O(K) ： 搜索过程中的递归深度不超过 KK ，因此系统因函数调用累计使用的栈空间占用 O(K) （因为函外空间。

    类似题型

    79.单词搜索https://leetcode.cn/problems/word-search