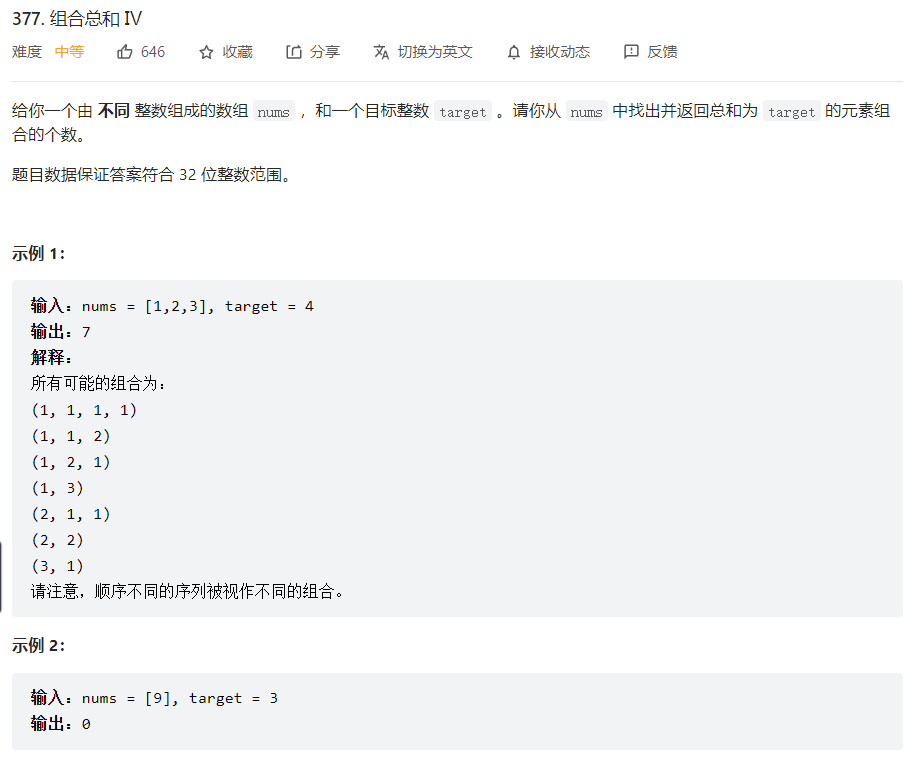
题目描述

解题思路

本题可以多次将数字放入，所以是多重背包问题。

• 确定dp数组以及下标的含义

dp[i]: 凑成目标正整数为i的排列个数为dp[i]

• 确定递推公式

dp[i]（考虑nums[j]）可以由 dp[i - nums[j]]（不考虑nums[j]） 推导出来。因为只要得到nums[j]，排列个数dp[i - nums[j]]，就是dp[i]的一部分。求装满背包有几种方法，递推公式一般都是dp[i] += dp[i - nums[j]]。

• 初始化

dp[0]在求方法一半初始化为0，为了递推公式。

• 遍历顺序

如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。

• 打印dp数组

public int combinationSum4(int[] nums, int target) {
    // dp[i]表示总和是i的不同的组合有dp[i]钟
    int[] dp = new int[target + 1];
    dp[0] = 1;
    // 由于求的是排列，部分顺序，所以应该先背包，从而相当于排列问题
    for (int j = 0; j <= target; j++) {
        for (int i = 0; i < nums.length; i++) {
            if (j >= nums[i]) { // 背包容量大于商品才进行计算
                dp[j] += dp[j - nums[i]];
            }
        }
    }
    return dp[target];
}