简介

  • 时间复杂度：O(n!)，这个可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n n-1 n-2 * ….. 1 = n!。

  • 空间复杂度：O(n)，和子集问题同理。

    46.全排列

    题目描述

    image.png

    解题思路

    注意全排列和组合问题不一样的地方就是组合可以选取前面的数，也就是不受startIndex的限制，所以for从0开始循环。但是又遇到了一个问题，就是不能选取本身，所以需要树层去重。

  • 递归函数参数

首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

  • 递归终止条件

叶子节点就是结果，当path的长度和数组长度相等时，那么此时选择到了一个结果。

  • 单层搜索的逻辑

这里和77.组合问题、131.切割问题和78.子集问题最大的不同就是for循环里不用startIndex了。
因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。
而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。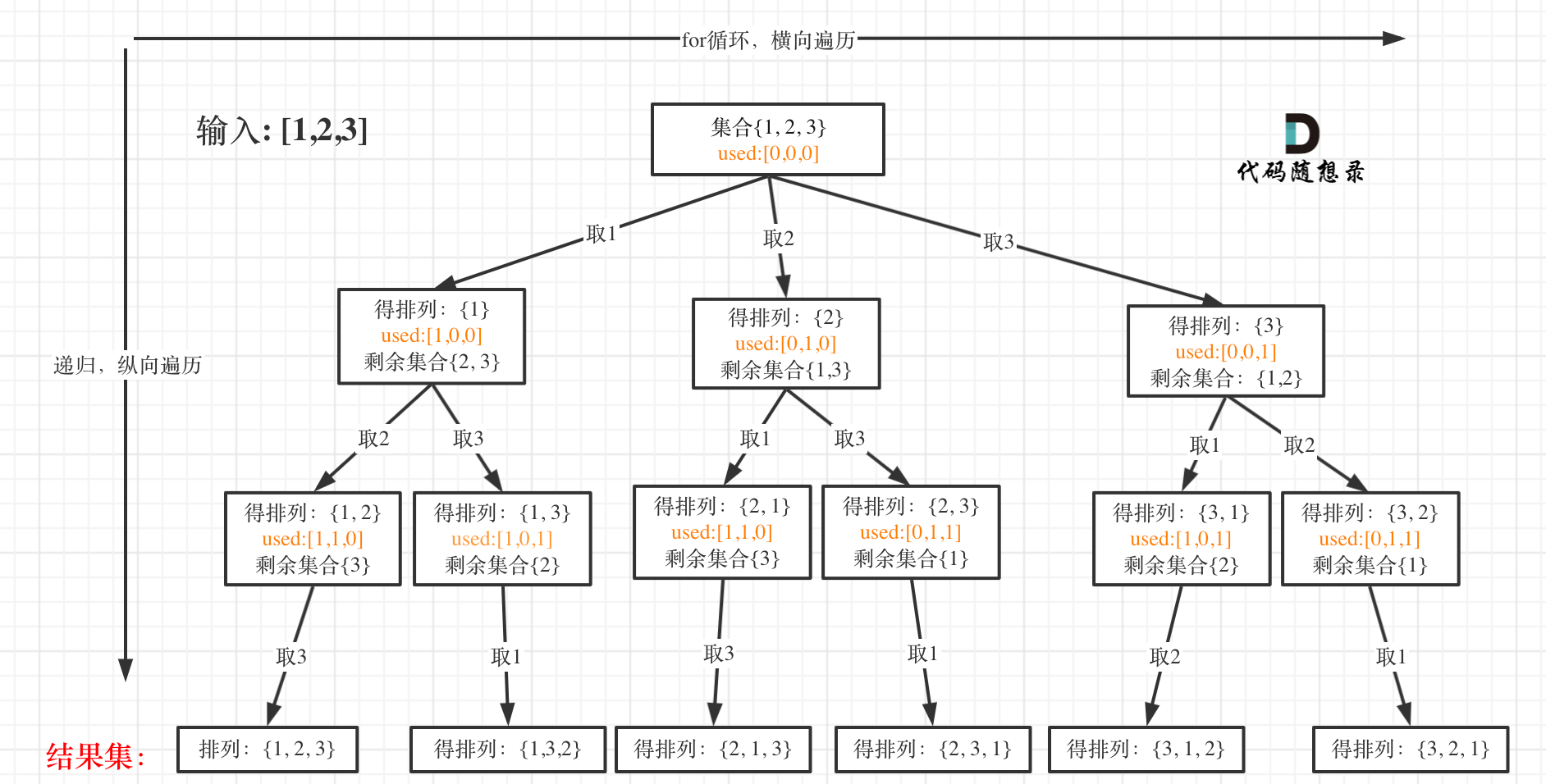
image.png

  1. public List<List<Integer>> permute(int[] nums) {
  2.     if (nums.length == 0) {
  3.         return res;
  4.     }
  5.     backtracking(nums, new boolean[nums.length]);
  6.     return res;
  7. }
  9. List<List<Integer>> res = new ArrayList<>();
  10. LinkedList<Integer> path = new LinkedList<>();
  12. public void backtracking(int[] nums, boolean[] used) {
  13.     if (path.size() == nums.length) {
  14.         res.add(new ArrayList<>(path));
  15.         return;
  16.     }
  18.     for (int i = 0; i < nums.length; i++) {    // 注意以前选择过的可以被选择，所以从0开始遍历
  19.         if (used[i]) continue;
  20.         path.add(nums[i]);
  21.         used[i] = true;
  22.         backtracking(nums, used);
  23.         used[i] = false;
  24.         path.removeLast();
  25.     }
  26. }

47.全排列 II

题目描述

image.png

解题思路

这道题目和46.全排列的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。
此题题目给的数组是可以重复的，但排序结果又不重复，所以需要树枝和树层同时去重。
去重方法前面讲过，套用即可。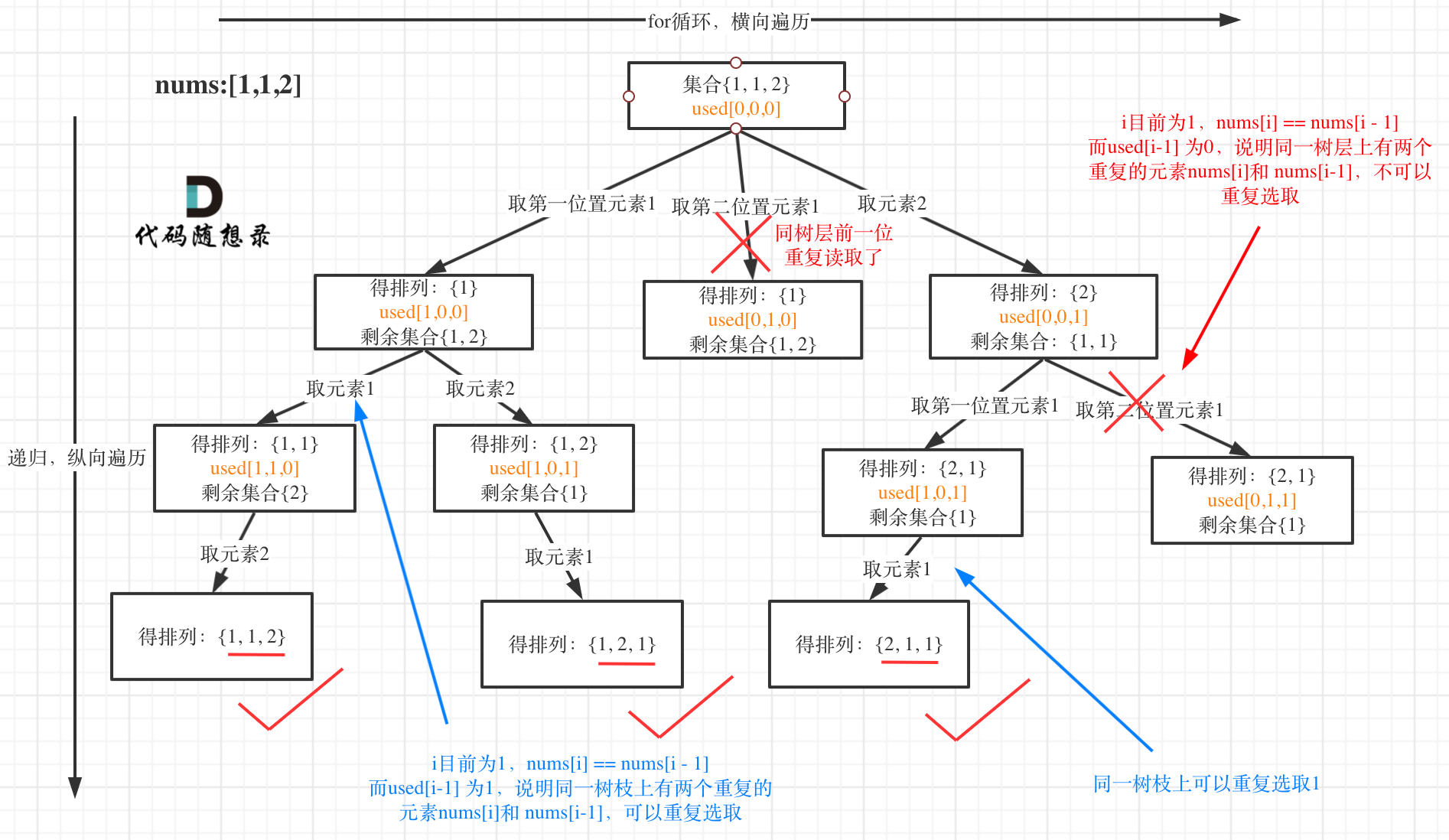
image.png

使用used来进行树层去重，注意需要排序

  1. public List<List<Integer>> permuteUnique(int[] nums) {
  2.     if (nums.length == 0) {
  3.         return res;
  4.     }
  5.     Arrays.sort(nums);
  6.     backtracking(nums, new boolean[nums.length]);
  7.     return res;
  8. }
  10. List<List<Integer>> res = new ArrayList<>();
  11. LinkedList<Integer> path = new LinkedList<>();
  13. public void backtracking(int[] nums, boolean[] used) {
  14.     if (path.size() == nums.length) {
  15.         res.add(new ArrayList<>(path));
  16.         return;
  17.     }
  19.     for (int i = 0; i < nums.length; i++) { // 排列从0开始
  20.         // used[i] == true，说明同一树枝nums[i - 1]使用过
  21.         // used[i - 1] == false，说明同一树层nums[i - 1]使用过
  22.         // 如果同一树层nums[i - 1]使用过则直接跳过
  23.         // 注意需要排列
  24.         if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {  // 后一个在同一层判断上一个是否使用过
  25.             continue;
  26.         }
  28.         // 此时时used[i]判断这个元素是否使用过（树枝去重）
  29.         if (used[i] == true) {
  30.             continue;       // 前一个判断path中是否使用过
  31.         }
  33.         path.add(nums[i]);
  34.         used[i] = true;
  35.         backtracking(nums, used);
  36.         used[i] = false;
  37.         path.removeLast();
  38.     }
  39. }

使用哈希表进行树层去重

  1. public List<List<Integer>> permuteUnique(int[] nums) {
  2.             if (nums.length == 0) {
  3.                 return res;
  4.             }
  5.             backtracking(nums, new boolean[nums.length]);
  6.             return res;
  7.         }
  9.         List<List<Integer>> res = new ArrayList<>();
  10.         LinkedList<Integer> path = new LinkedList<>();
  12.         /**
  13.          * 哈希法
  14.          *
  15.          * @param nums
  16.          * @param used
  17.          */
  18.         public void backtracking(int[] nums, boolean[] used) {
  19.             if (path.size() == nums.length) {
  20.                 res.add(new ArrayList<>(path));
  21.                 return;
  22.             }
  24.             Set<Integer> set = new HashSet<>();
  25.             for (int i = 0; i < nums.length; i++) {
  26.                 // 树层去重
  27.                 if (set.contains(nums[i])) {
  28.                     continue;
  29.                 }
  30.                 // 枝干去重
  31.                 if (used[i] == true) {
  32.                     continue;
  33.                 }
  34.                 set.add(nums[i]);
  35.                 used[i] = true;
  36.                 path.add(nums[i]);
  37.                 backtracking(nums, used);
  38.                 used[i] = false;    // 回溯
  39.                 path.removeLast();
  40.             }
  41.         }

剑指 Offer 38. 字符串的排列

题目描述

image.png

解题思路

树枝和树层去重，注意排序。

  1. class Solution {
  2.     public String[] permutation(String s) {
  3.         char[] array = s.toCharArray();
  4.         Arrays.sort(array);
  5.         backTracking(array, new boolean[s.length()]);
  6.         return list.toArray(new String[list.size()]);
  7.     }
  9.     List<String> list = new ArrayList<>();
  10.     StringBuilder sb = new StringBuilder();
  12.     public void backTracking(char[] array, boolean[] used) {
  13.         if (sb.length() >= array.length) {
  14.             list.add(sb.toString());
  15.             return;
  16.         }
  18.         for (int i = 0; i < array.length; i++) {
  19.             if (i > 0 && array[i] == array[i - 1] && used[i - 1] == false) continue;
  20.             if (used[i] == true) continue;
  21.             sb.append(array[i]);
  22.             used[i] = true;
  23.             backTracking(array, used);
  24.             used[i] = false;
  25.             sb.deleteCharAt(sb.length() - 1);
  26.         }
  27.     }
  28. }

剑指 Offer 17. 打印从 1 到最大的 n 位数

具体见链接🔗