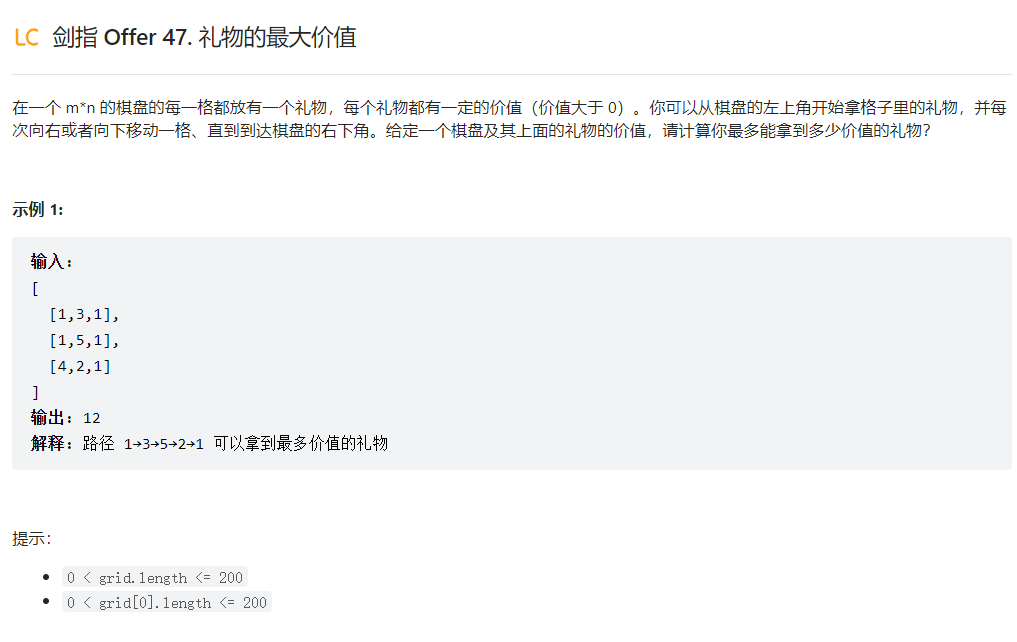
题目描述

image.png

解题思路

  • dp[i][j]表示下标i-1和j-1的礼物的价值
  • 递推公式

此处根据题意可得，dp[i][j]需要根据上边和左边推出，且取最大值，所以dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];

  • 初始化

第一行依次相加，第一列也是。

  • 遍历顺序

根据递推公式可以得知从上到下，从左到右。

  • 打印dp数组

…

  1. public int maxValue(int[][] grid) {
  2.     // dp[i][j]表示下标i-1和j-1的礼物的价值
  3.     int[][] dp = new int[grid.length][grid[0].length];
  5.     // 初始化
  6.     dp[0][0] = grid[0][0];
  7.     for (int i = 1; i < grid.length; i++) dp[i][0] = grid[i][0] + dp[i - 1][0];
  8.     for (int i = 1; i < grid[0].length; i++) dp[0][i] = grid[0][i] + dp[0][i - 1];
  10.     for (int i = 1; i < grid.length; i++) {
  11.         for (int j = 1; j < grid[0].length; j++) {
  12.             dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
  13.         }
  14.     }
  16.     return dp[grid.length - 1][grid[0].length - 1];
  17. }

优化空间复杂度为O(1)

  1. public int maxValue(int[][] grid) {
  2.     for (int i = 0; i < grid.length; i++) {
  3.         for (int j = 0; j < grid[0].length; j++) {
  4.             if (i == 0 && j == 0) continue;
  5.             if (i == 0) grid[0][j] += grid[0][j - 1];
  6.             else if (j == 0) grid[i][0] += grid[i - 1][0];
  7.             else grid[i][j] += Math.max(grid[i - 1][j], grid[i][j - 1]);
  8.         }
  9.     }
  11.     return grid[grid.length - 1][grid[0].length - 1];
  12. }