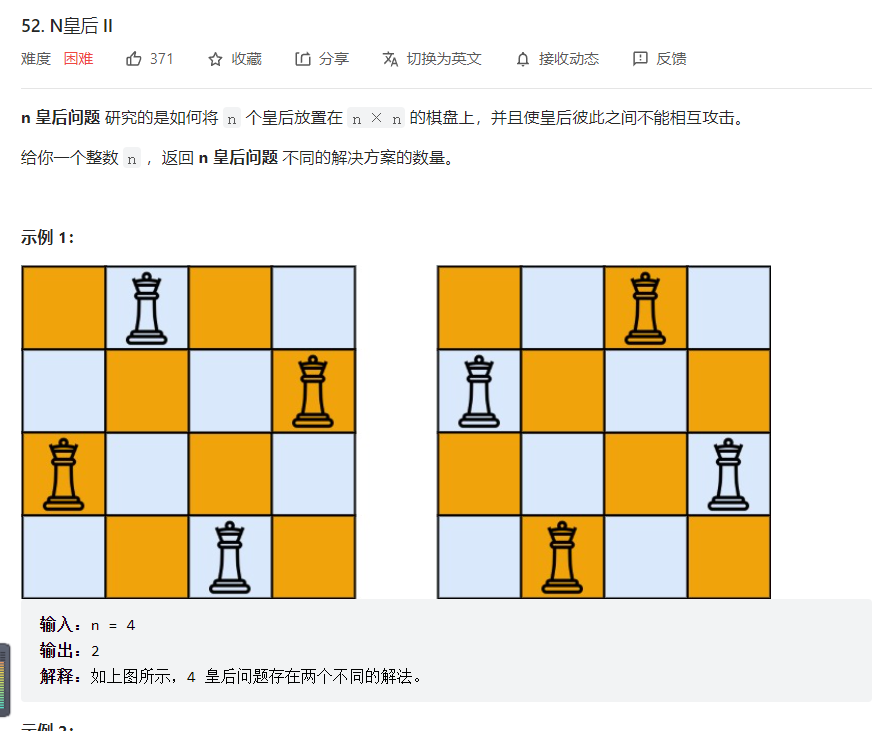
简介

N皇后问题分析：

时间复杂度：O(n!) ，其实如果看树形图的话，直觉上是O(n^n)，但皇后之间不能见面所以在搜索的过程中是有剪枝的，最差也就是O（n!），n!表示n (n-1) …. * 1。
空间复杂度：O(n)，和子集问题同理。

解数独问题分析：

时间复杂度：O(9^m) , m是’.’的数目。
空间复杂度：O(n^2)，递归的深度是n^2

51. N 皇后

题目描述

解题思路
递归函数参数

我依然是定义全局变量二维数组result来记录最终结果。
参数n是棋盘的大小，然后用row来记录当前遍历到棋盘的第几层了。

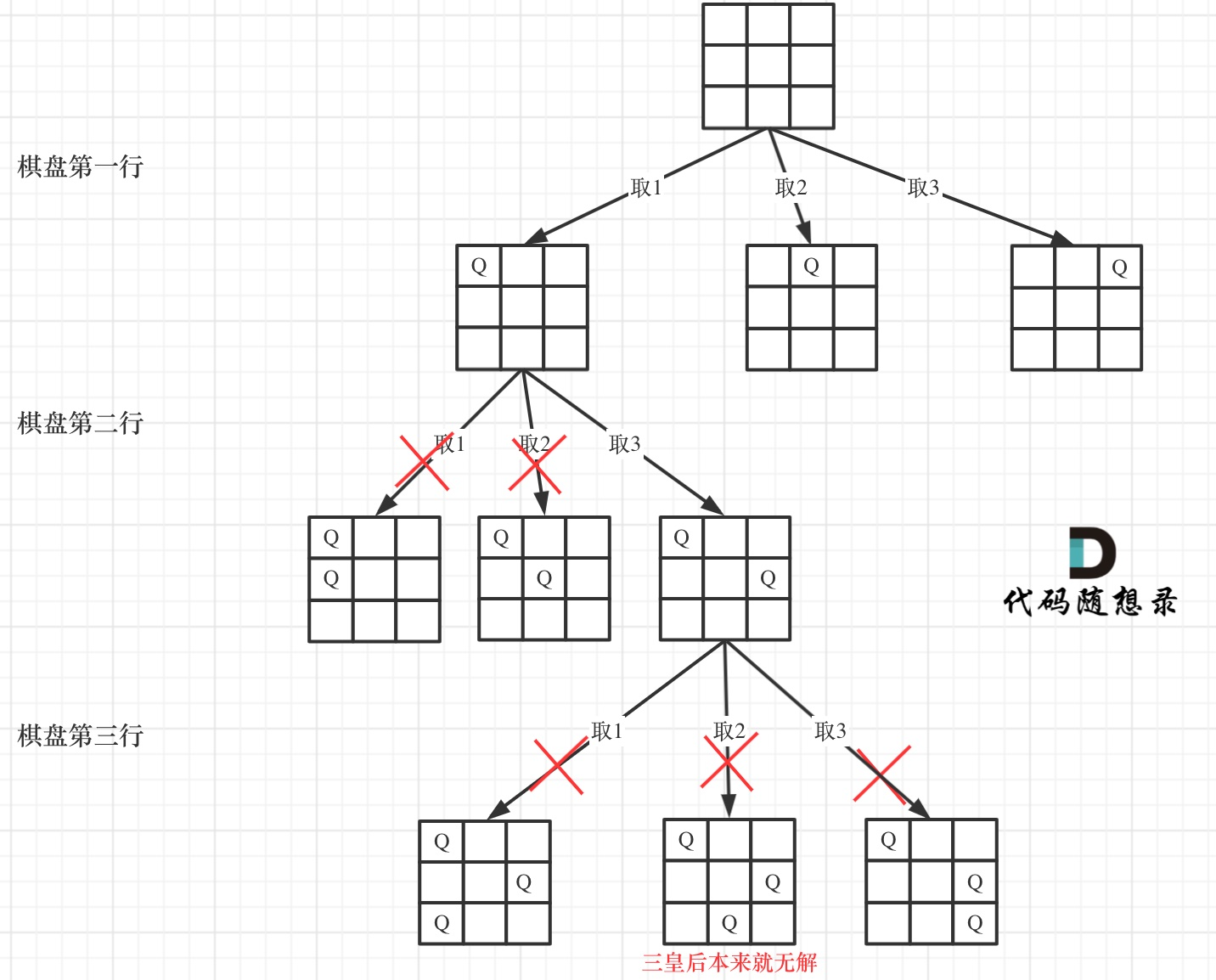
递归终止条件:

可以看出，当递归到棋盘最底层（也就是叶子节点）的时候，就可以收集结果并返回了。

单层搜索的逻辑

递归深度就是row控制棋盘的行，每一层里for循环的col控制棋盘的列，一行一列，确定了放置皇后的位置。
每次都是要从新的一行的起始位置开始搜，所以都是从0开始。
验证棋盘是否合法
按照如下标准去重：

不能同行
不能同列
不能同斜线（45度和135度角）

public List<List<String>> solveNQueens(int n) {
    if (n == 0) {
        return res;
    }
    // 需要将二维数组全部赋值，防止出现空字符
    char[][] chars = new char[n][n];
    for (char[] num : chars) {
        Arrays.fill(num, '.'); // 将指定的char值分配给指定的char数组的每个元素
    }
    backtracking(n, 0, chars);
    return res;
}
List<List<String>> res = new ArrayList<>();*/
    /**
         * 回溯搜索
         *
         * @param n          表示输入的棋盘大小
         * @param row        表示当前遍历到第几行了
         * @param chessboard 表示棋盘（ ‘.’ 表示空格，‘Q’表示皇后）
         */
    public void backtracking(int n, int row, char[][] chessboard) {
    if (row == n) {
        res.add(numToList(chessboard));// 此行
        return;
    }
    for (int col = 0; col < n; col++) {   // for遍历每列
        if (isValid(row, col, n, chessboard)) {
            chessboard[row][col] = 'Q'; // 放置皇后
            backtracking(n, row + 1, chessboard); // 递归遍历每行，注意row需要加一
            chessboard[row][col] = '.'; // 回溯
        }
    }
}
/**
         * 二维字符数组转化为List集合
         *
         * @param chessboard
         * @return
         */
public List<String> numToList(char[][] chessboard) {
    List<String> list = new ArrayList<>();
    for (char[] num : chessboard) {
        list.add(String.valueOf(num));
    }
    return list;
}
/**
         * 判断是否满足n皇后的条件
         *
         * @param row
         * @param col
         * @param chessboard
         * @return
         */
public boolean isValid(int row, int col, int n, char[][] chessboard) {
    // 判断一列一列是否有皇后
    for (int i = 0; i < row; i++) {
        if (chessboard[i][col] == 'Q')
            return false;
    }
    // 判断135度是否有皇后
    for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
        if (chessboard[i][j] == 'Q')
            return false;
    }
    // 判断45度是否有皇后
    for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
        if (chessboard[i][j] == 'Q')
            return false;
    }
    return true;
}

在这份代码中，细心的同学可以发现为什么没有在同行进行检查呢？
因为在单层搜索的过程中，每一层递归，只会选for循环（也就是同一行）里的一个元素，所以不用去重了。

52. N皇后 II

题目描述

解题思路

和上一题求解方式一直，但取结果时只取多少种。

class Solution {
    public int totalNQueens(int n) {
        char[][] chessboard = new char[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(chessboard[i], '.');
        }
        backtracking(n, 0, chessboard);
        return result;
    }
    int result = 0;
    public boolean backtracking(int n, int row, char[][] chessboard) {
        if (row == n) {
            result++;
            return true;
        }
        for (int i = 0; i < n; i++) {
            if (isValid(chessboard, n, row, i)) {
                chessboard[row][i] = 'Q';
                backtracking(n, row + 1, chessboard);
                chessboard[row][i] = '.';
            }
        }
        return false;
    }
    public boolean isValid(char[][] chessboard, int n, int row, int col) {
        int i = 0, j = 0;
        for (i = 0; i < row; i++) {
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }
        for (i = row - 1, j = col - 1; i >= 0 && j      >= 0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        for (i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }
}

37. 解数独

题目描述

解题思路

N皇后问题是因为每一行每一列只放一个皇后，只需要一层for循环遍历一行，递归来来遍历列，然后一行一列确定皇后的唯一位置。
本题就不一样了，本题中棋盘的每一个位置都要放一个数字，并检查数字是否合法，解数独的树形结构要比N皇后更宽更深。

递归函数以及参数

递归函数的返回值需要是bool类型，为什么呢？
因为解数独找到一个符合的条件（就在树的叶子节点上）立刻就返回，相当于找从根节点到叶子节点一条唯一路径，所以需要使用bool返回值，这一点在N皇后问题中已经介绍过了，一样的道理。

递归终止条件

本题递归不用终止条件，解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
不用终止条件会不会死循环？
递归的下一层的棋盘一定比上一层的棋盘多一个数，等数填满了棋盘自然就终止（填满当然好了，说明找到结果了），所以不需要终止条件！
那么有没有永远填不满的情况呢？
这个问题我在递归单层搜索逻辑里在来讲！

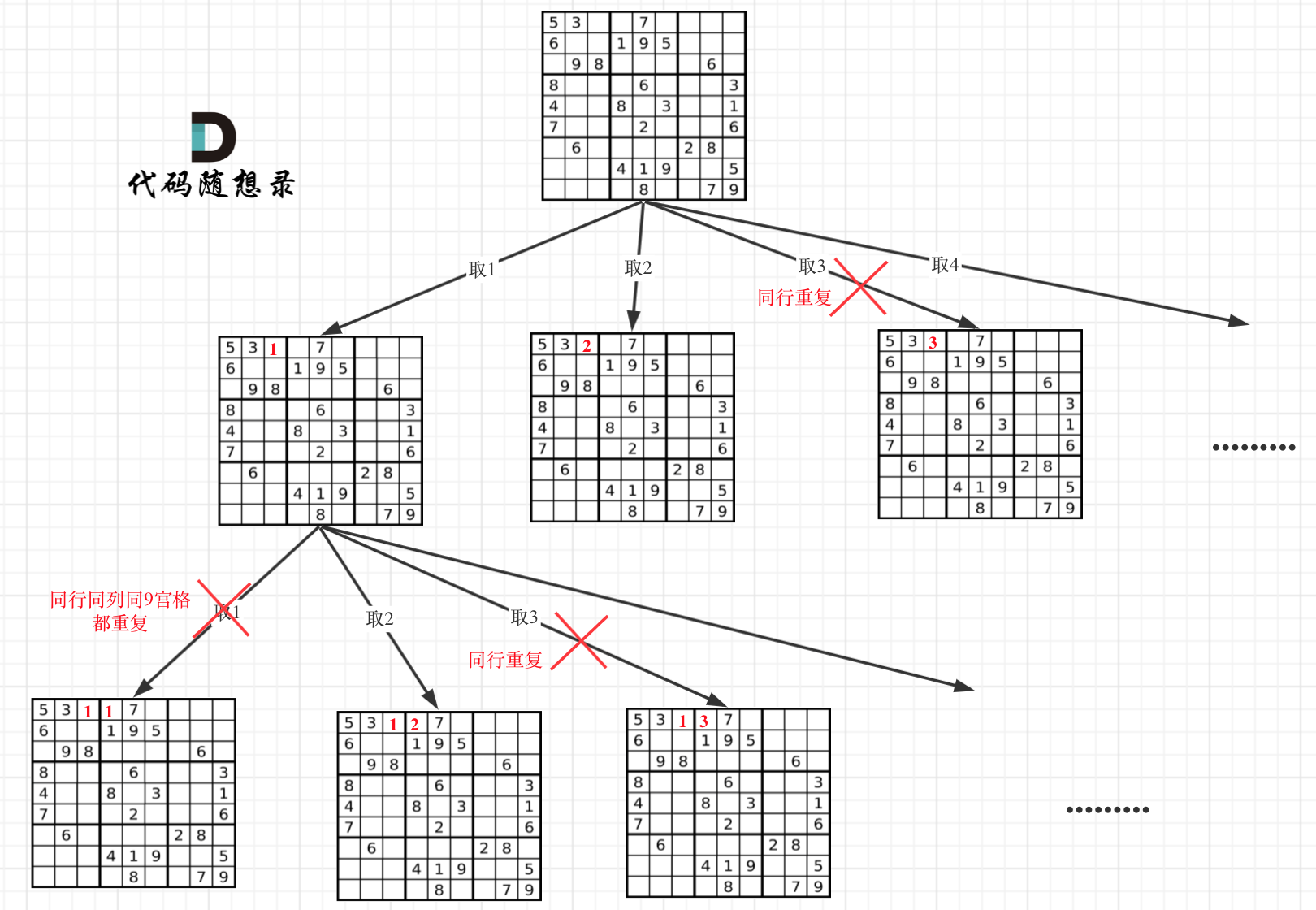
递归单层搜索逻辑

在树形图中可以看出我们需要的是一个二维的递归（也就是两个for循环嵌套着递归）
一个for循环遍历棋盘的行，一个for循环遍历棋盘的列，一行一列确定下来之后，递归遍历这个位置放9个数字的可能性！如果9个数字都不能填充进去，那么返回false，这就是没用终止条件也不会永远填不满棋盘而无限递归下去！
判断棋盘是否合法
判断棋盘是否合法有如下三个维度：

同行是否重复
同列是否重复
9宫格里是否重复

public void solveSudoku(char[][] board) {
    if (board == null) {
        return;
    }
    backtracking(board);
}
public boolean backtracking(char[][] board) {
    // 可以不需要返回条件，不符合会返回false
    // 遍历整个二维数组
    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board[0].length; j++) {
            if (board[i][j] != '.') continue;   // 此时位置已经有数字，跳过
            for (char k = '1'; k <= '9'; k++) {   // 依次判断数组 1~9
                if (isValid(i, j, k, board)) {
                    board[i][j] = k;
                    if (backtracking(board)) return true;   // 找到一条就返回
                    board[i][j] = '.';
                }
            }
            return false;   // 如果9个数字都不满足条件，那么此处此数独无解
        }
    }
    return true;    // 所有都遍历完没有返回false，满足条件
}
/**
         * 判断一行，一列，以及九宫格中是否有重复的数字
         *
         * @param row
         * @param col
         * @param val
         * @param board
         * @return
         */
public boolean isValid(int row, int col, char val, char[][] board) {
    // 判断一行
    for (int i = 0; i < board[row].length; i++) {
        if (board[row][i] == val) {
            return false;
        }
    }
    // 判断一列
    for (int i = 0; i < board.length; i++) {
        if (board[i][col] == val) {
            return false;
        }
    }
    // 判断九宫格
    int startRow = (row / 3) * 3;  // 行起始位置
    int startCol = (col / 3) * 3;  // 列起始位置
    for (int i = startRow; i < startRow + 3; i++) {
        for (int j = startCol; j < startCol + 3; j++) {
            if (board[i][j] == val) {
                return false;
            }
        }
    }
    return true;
}

Peanut的算法屋

棋盘问题

简介

51. N 皇后

题目描述

解题思路

52. N皇后 II

题目描述

解题思路

37. 解数独

题目描述

解题思路