题目描述

image.png

解题思路

本题可以转化为最长公共子序列的问题，如何转化呢？
绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！
直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。
拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：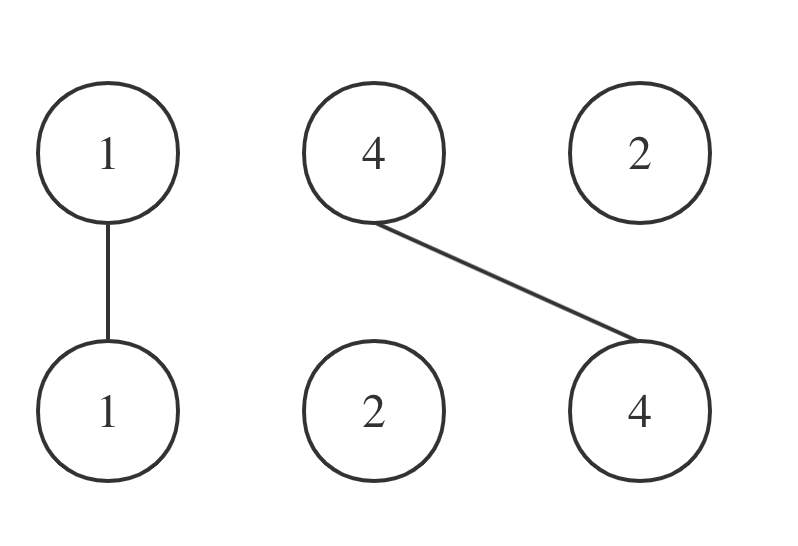
image.png
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）
也就是1如果对应了1，那么4对应的数字就应该在1的位置的后边，相对位置也就是在后边，所以本质就是一个不连续子序列问题。

  1. /**
  2.          * 找两个不相交的线，相当于找最大公共子序列，lc 1143
  3.          *
  4.          * @param nums1
  5.          * @param nums2
  6.          * @return
  7.          */
  8. public int maxUncrossedLines(int[] nums1, int[] nums2) {
  9.     int[][] dp = new int[nums1.length + 1][nums2.length + 1];
  10.     dp[0][0] = 0;
  12.     for (int i = 1; i <= nums1.length; i++) {
  13.         for (int j = 1; j <= nums2.length; j++) {
  14.             if (nums1[i - 1] == nums2[j - 1]) {
  15.                 dp[i][j] = dp[i - 1][j - 1] + 1;
  16.             } else {
  17.                 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
  18.             }
  19.         }
  20.     }
  21.     return dp[nums1.length][nums2.length];
  22. }