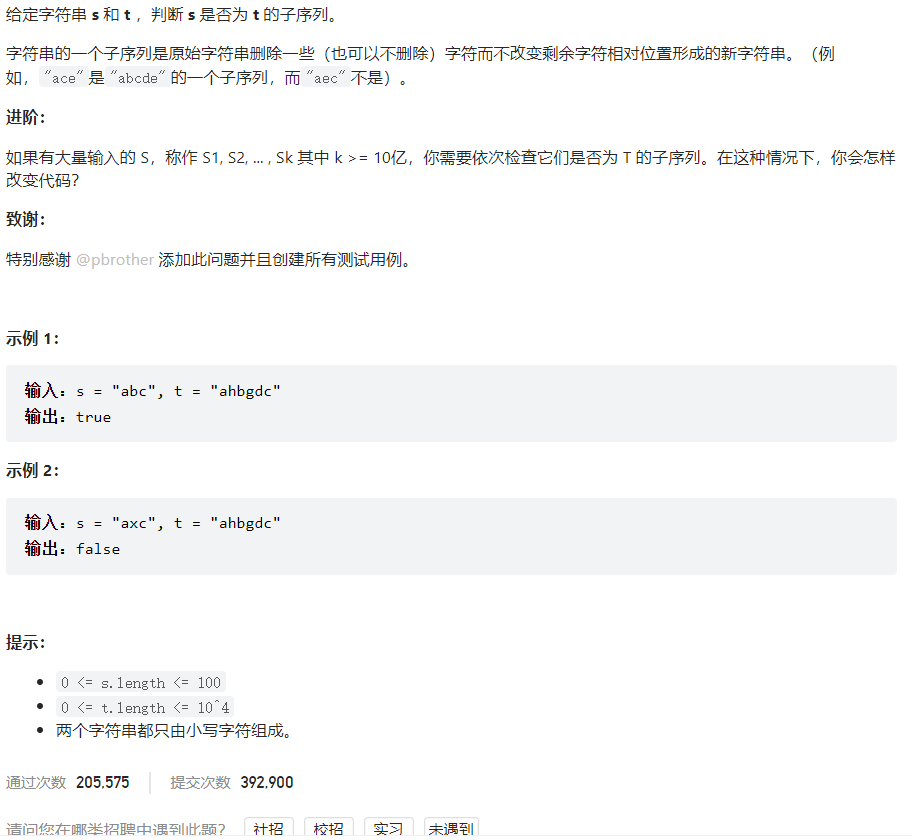
题目描述

image.png

解题思路

  • dp数组含义

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

  • 确定递推公式

在确定递推公式的时候，首先要考虑如下两种操作，整理如下：

  • if (s[i - 1] == t[j - 1])
    • t中找到了一个字符在s中也出现了，此时就是s[i-2]和t[j-2]的子序列长度加一。dp[i][j] = dp[i - 1][j - 1] + 1;
  • if (s[i - 1] != t[j - 1])
    • 相当于t要删除元素，继续匹配，此时应该就是s[j-2]的子序列长度，即dp[i][j] = dp[i][j - 1];
      • 初始化

可以由题推出，如果哪一边长度为0，那么子序列长度也就是0。所以都初始化为0。

  • 遍历顺序

同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序也应该是从上到下，从左到右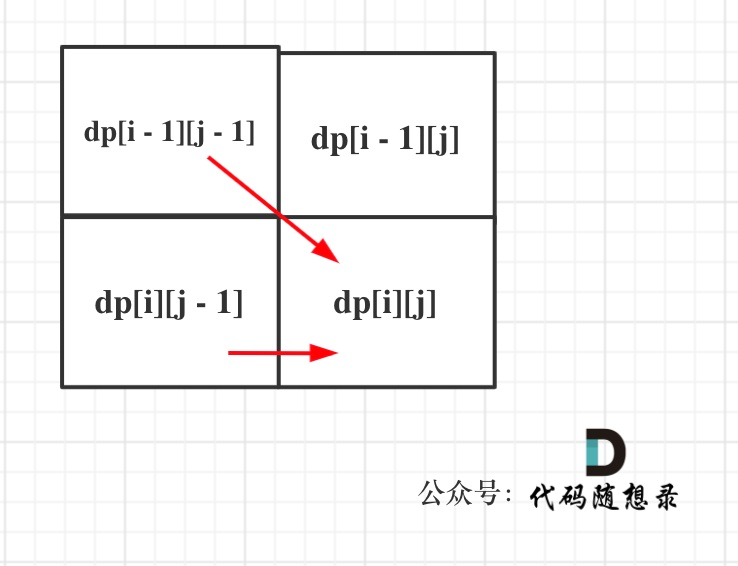
image.png

  • 举例推导dp数组

以示例一为例，输入：s = “abc”, t = “ahbgdc”，dp状态转移图如下：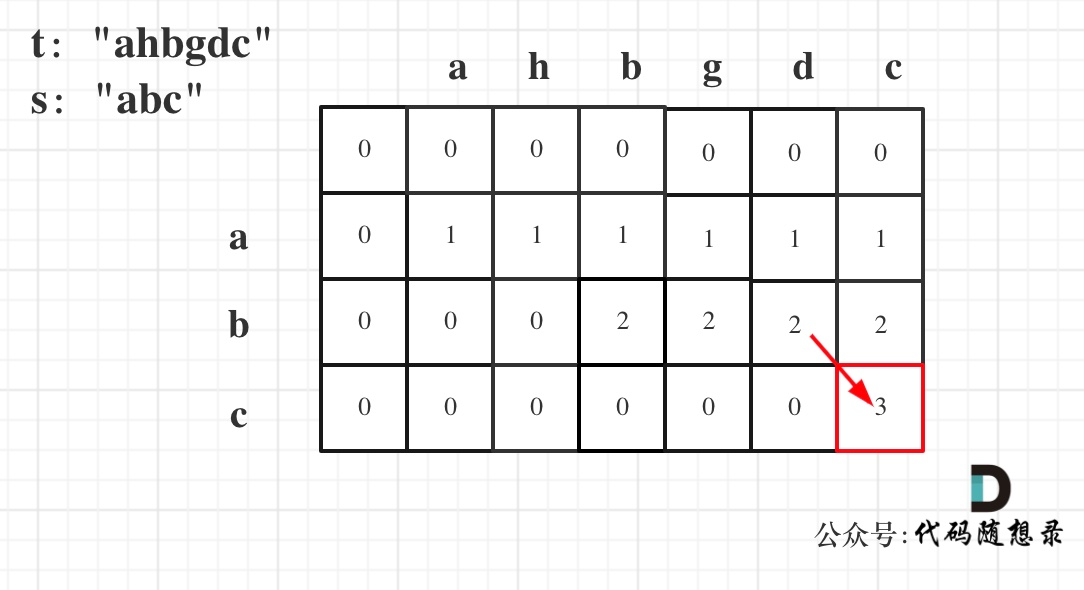
image.png
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度，所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明：s与t的最长相同子序列就是s，那么s 就是 t 的子序列。
图中dp[s.size()][t.size()] = 3， 而s.size() 也为3。所以s是t 的子序列，返回true。
最后判断如果相同子序列长度等于s的长度，那么s就是t的子序列。

  1. public boolean isSubsequence(String s, String t) {
  2.     // dp[i][j]表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]
  3.     int[][] dp = new int[s.length() + 1][t.length() + 1];
  4.     // 初始化左上两边
  5.     for (int i = 0; i < s.length() + 1; i++) {
  6.         dp[i][0] = 0;
  7.     }
  9.     for (int i = 0; i < t.length() + 1; i++) {
  10.         dp[0][i] = 0;
  11.     }
  13.     for (int i = 1; i < s.length() + 1; i++) {
  14.         for (int j = 1; j < t.length() + 1; j++) {
  15.             //                    if (s[i - 1] == t[j - 1])
  16.             //                        t中找到了一个字符在s中也出现了
  17.             //                    if (s[i - 1] != t[j - 1])
  18.             //                        相当于t要删除元素，继续匹配
  19.             if (s.charAt(i - 1) == t.charAt(j - 1)) {
  20.                 dp[i][j] = dp[i - 1][j - 1] + 1; // 相同子序列数加一，表示s中又有一个字母在t中
  21.             } else {
  22.                 dp[i][j] = dp[i][j - 1];    // 不相等时，子序列的长度不变
  23.             }
  24.         }
  25.     }
  27.     return dp[s.length()][t.length()] == s.length() ? true : false;
  28. }