62. 不同路径

题目描述

image.png

解题思路

回溯法

超时

动态规划

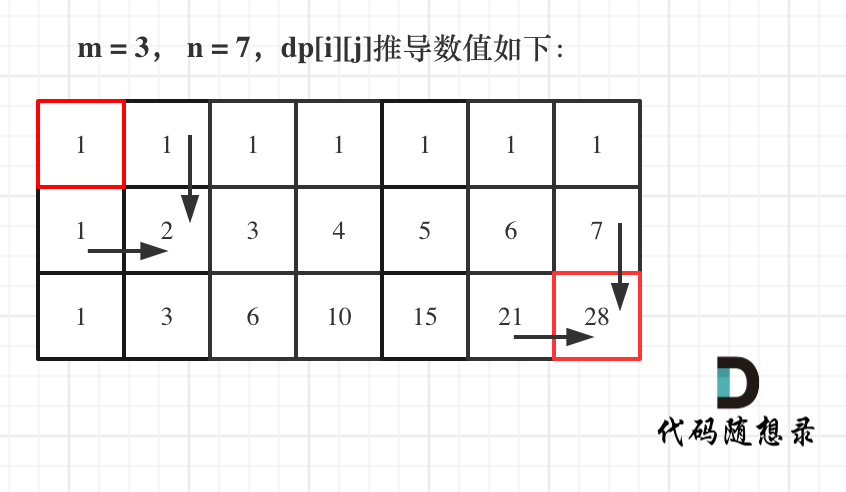
  • 确定dp数组（dp table）以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

  • 确定递推公式

想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。
那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

  • dp数组的初始化

如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。

  • 遍历顺序

由递推公式可以得知从上和从左推出，所以从左往右和从右往左遍历。

  • 打印DP数组

image.png

  1. /**
  2.          * 1. 确定dp数组下标含义 dp[i][j] 到每一个坐标可能的路径种类
  3.          * 2. 递推公式 dp[i][j] = dp[i-1][j] dp[i][j-1]
  4.          * 3. 初始化 dp[i][0]=1 dp[0][i]=1 初始化横竖就可
  5.          * 4. 遍历顺序 一行一行遍历
  6.          * 5. 推导结果 。。。。。。。。
  7.          *
  8.          * @param m
  9.          * @param n
  10.          * @return
  11.          */
  12. public int uniquePaths(int m, int n) {
  13.     int[][] dp = new int[m][n];
  15.     // 初始化dp数组，2个边界都只有一条路径
  16.     for (int i = 0; i < m; i++) {
  17.         dp[i][0] = 1;
  18.     }
  20.     for (int j = 0; j < n; j++) {
  21.         dp[0][j] = 1;
  22.     }
  24.     for (int i = 1; i < m; i++) {
  25.         for (int j = 1; j < n; j++) {
  26.             dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
  27.         }
  28.     }
  30.     return dp[m - 1][n - 1];
  31. }

优化为一位数组

  1. /**
  2.          * 优化为一维数组
  3.          *
  4.          * @param m
  5.          * @param n
  6.          * @return
  7.          */
  8. public int uniquePaths(int m, int n) {
  9.     int[] dp = new int[n];
  11.     // 初始化dp数组
  12.     for (int i = 0; i < n; i++) {
  13.         dp[i] = 1;
  14.     }
  16.     for (int j = 1; j < m; j++) {
  17.         for (int i = 1; i < n; i++) {
  18.             dp[i] += dp[i - 1];  // dp[i]代表上边一行，dp[i-1]代表左边一列
  19.         }
  20.     }
  22.     return dp[n - 1];
  23. }

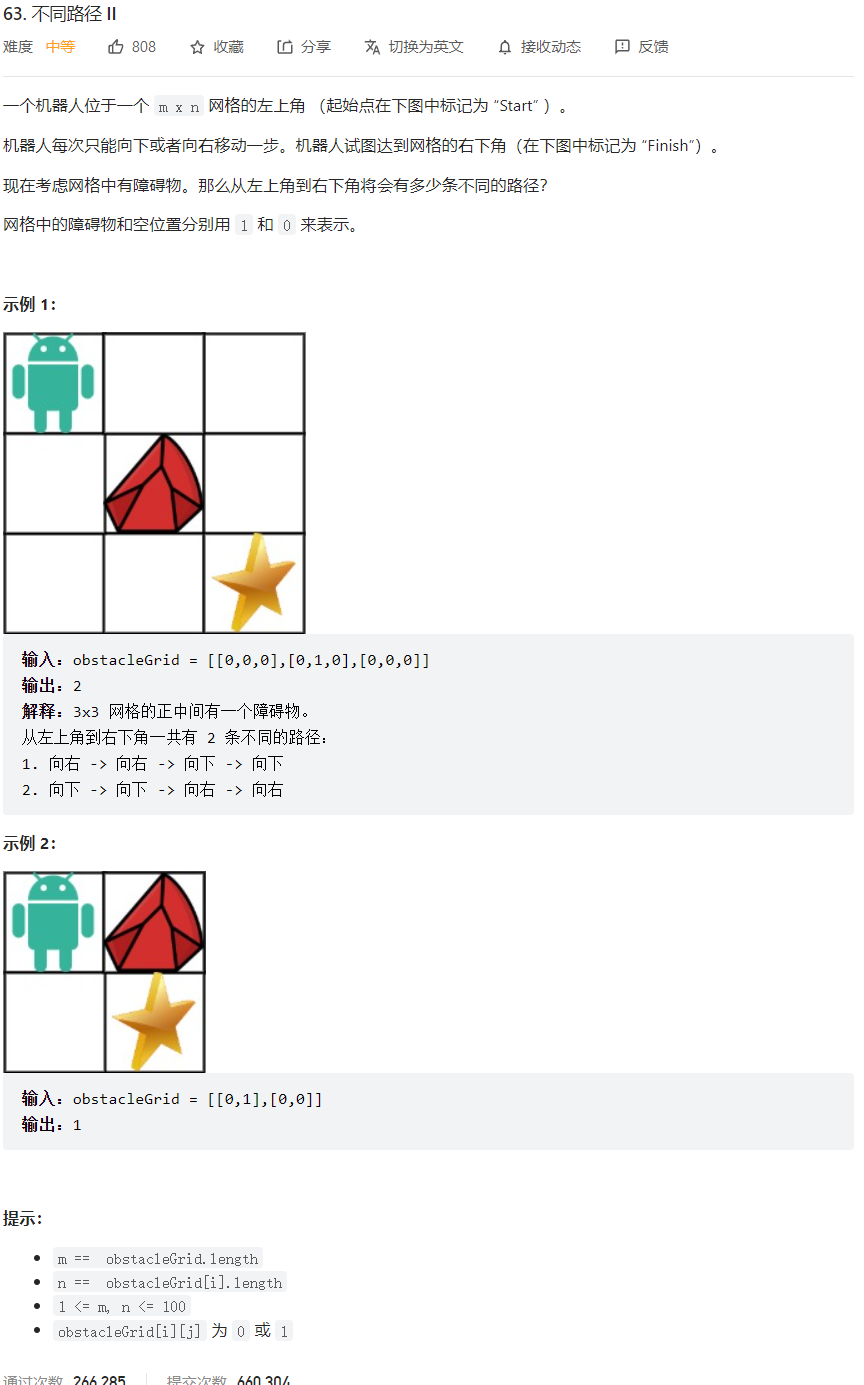
63. 不同路径 II

题目描述

image.png

解题思路

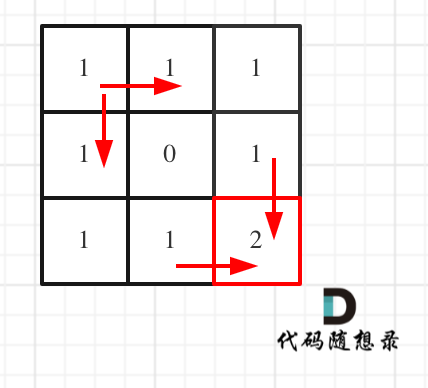
此时和上一题的最大区别就是由障碍物，如果遇到障碍物的话，此时障碍物的路径就是0条。
初始化的话在障碍物的后边都没有路径。其他步骤和62题一致，在遇到障碍物时也不需要遍历，直接跳过。
举例：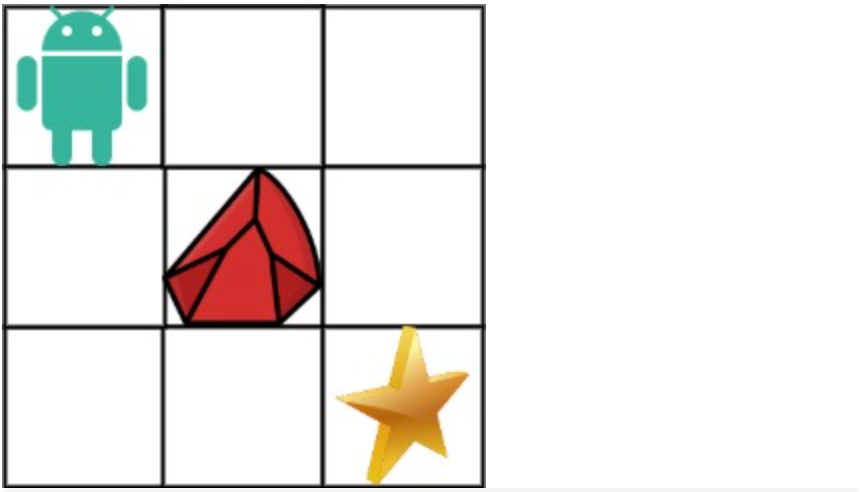
image.png
image.png

  1. /**
  2.          * dp
  3.          *
  4.          * @param obstacleGrid
  5.          * @return
  6.          */
  7. public int uniquePathsWithObstacles(int[][] obstacleGrid) {
  8.     int[][] dp = new int[obstacleGrid.length][obstacleGrid[0].length];
  10.     // 初始化dp数组，遇到障碍后，后面的路径都是0
  11.     for (int i = 0; i < obstacleGrid.length && obstacleGrid[i][0] == 0; i++) {
  12.         dp[i][0] = 1;
  13.     }
  15.     for (int j = 0; j < obstacleGrid[0].length && obstacleGrid[0][j] == 0; j++) {
  16.         dp[0][j] = 1;
  17.     }
  19.     for (int i = 1; i < obstacleGrid.length; i++) {
  20.         for (int j = 1; j < obstacleGrid[0].length; j++) {
  21.             if (obstacleGrid[i][j] == 1) continue;  // 遇到石头时，跳过此次循环，所以就 默认为0
  22.             dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
  23.         }
  24.     }
  26.     return dp[obstacleGrid.length - 1][obstacleGrid[0].length - 1];
  27. }