题目描述

image.png

解题思路

DP

  • dp数组表示的含义

dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

  • 确定递推公式

将数分解为两个数相乘，即为(i - j) j ，如果分解为两个以上的数相乘那么就是dp[i - j] j。
j是从1开始遍历，拆分j的情况，在遍历j的过程中其实都计算过了。那么从1遍历j，比较(i - j) j和dp[i - j] j 取最大的。递推公式：dp[i] = max(dp[i], max((i - j) j, dp[i - j] j));

  • 初始化

dp[0]和dp[1]是没有意义的，所以初始化dp[2]为1

  • 确定遍历顺序

确定遍历顺序，先来看看递归公式：dp[i] = max(dp[i], max((i - j) j, dp[i - j] j));
dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]。

  • 举例推导dp数组

举例当n为10 的时候，dp数组里的数值，如下：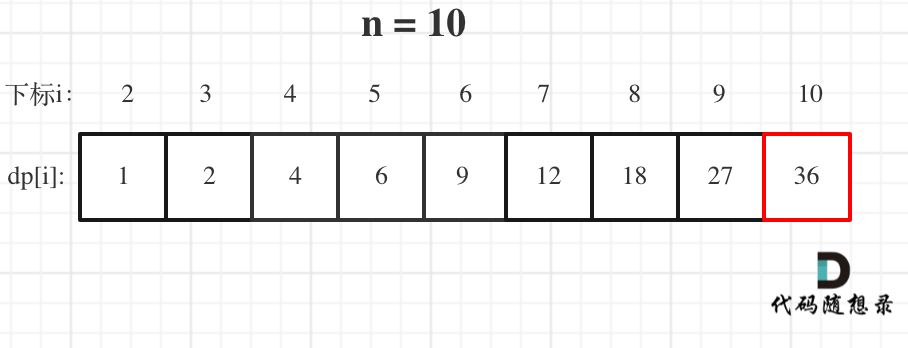
image.png

  1. /**
  2.          * 动态规划
  3.          *
  4.          * @param n
  5.          * @return
  6.          */
  7. public int integerBreak(int n) {
  8.     // dp[i]表示整数为i，被拆分之后相乘的最大值
  9.     int[] dp = new int[n + 1];
  11.     // 初始化
  12.     // dp[0] 和 dp[1] 0和1无法被拆分，所以不需要初始化
  13.     // 应该初始化dp[2]
  14.     dp[2] = 1;
  16.     // 遍历是从前向后，现有dp[i - j] 才会有 dp[i]
  17.     for (int i = 3; i <= n; i++) {  // 遍历i，构造dp数组
  18.         for (int j = 1; j < i - 1; j++) {   // 遍历j，找i中拆分出来的数
  19.             // 递推公式
  20.             // j * (i - j)表示两个数相乘
  21.             // dp[i - j] * j表示两个或者两个数以上相乘
  22.             // 与dp[i]比较的意思是，遍历j的时候找出最大相乘的数，赋值给dp[i]
  23.             dp[i] = Math.max(dp[i], Math.max(dp[i - j] * j, j * (i - j)));
  24.         }
  25.     }
  27.     return dp[n];
  28. }

贪心

本题也可以用贪心，每次拆成n个3，如果剩下是4，则保留4，然后相乘，但是这个结论需要数学证明其合理性！

  1. public int integerBreak(int n) {
  2.     if (n == 2) return 1;
  3.     if (n == 3) return 2;
  4.     if (n == 4) return 4;
  6.     int result = 1;
  7.     while (n > 4) {
  8.         result *= 3;
  9.         n -= 3;
  10.     }
  11.     result *= n;
  13.     return result;
  14. }

类似题型

剑指 Offer 14- I. 剪绳子

题目描述

🔗
image.png

解题思路

和上面一题一个做法

  1. // 动态规划
  2. public int cuttingRope(int n) {
  3.     int[] dp = new int[n + 1];
  4.     dp[1] = 1;
  5.     dp[2] = 1;
  7.     for (int i = 3; i <= n; i++) {
  8.         for (int j = 1; j < i; j++) {
  9.             dp[i] = Math.max(dp[i], Math.max((i - j) * j, dp[i - j] * j));
  10.         }
  11.     }
  13.     return dp[n];
  14. }