题目描述

解题思路

二分法

为精简篇幅，本文将数组 numbersnumbers 缩写为 numsnums 。

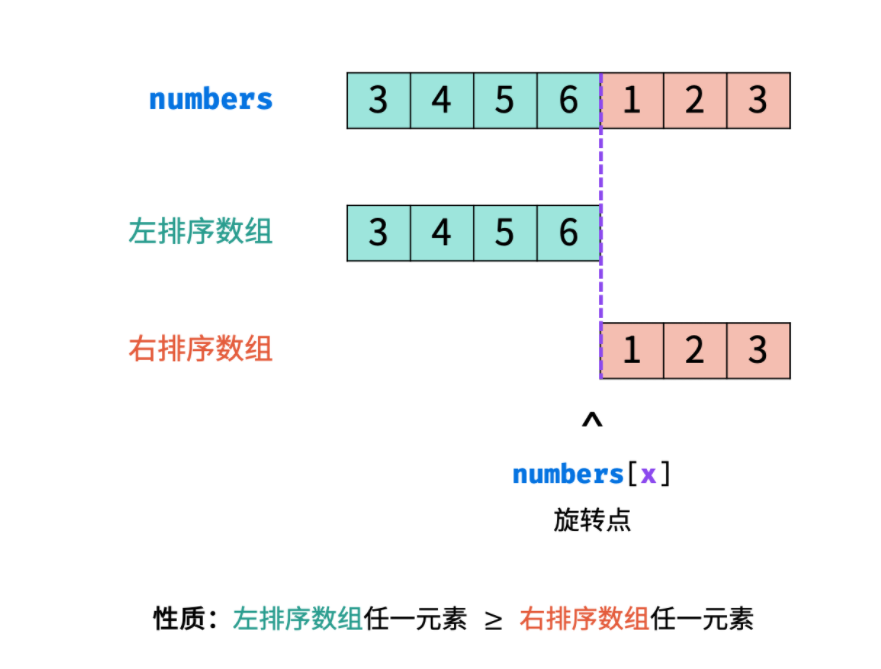
如下图所示，寻找旋转数组的最小元素即为寻找 右排序数组 的首个元素 nums[x]nums[x] ，称 xx 为 旋转点 。

排序数组的查找问题首先考虑使用 二分法 解决，其可将 遍历法 的 线性级别 时间复杂度降低至 对数级别 。

算法流程：

• 初始化： 声明 ii, jj 双指针分别指向 numsnums 数组左右两端；
• 循环二分： 设 m = (i + j) / 2m=(i+j)/2 为每次二分的中点（ “/“ 代表向下取整除法，因此恒有 i≤m<j ），可分为以下三种情况：
  • 当 nums[m] > nums[j]nums[m]>nums[j] 时： mm 一定在 左排序数组 中，即旋转点 xx 一定在 [m + 1, j][m+1,j] 闭区间内，因此执行 i = m + 1i=m+1；
  • 当 nums[m] < nums[j]nums[m]<nums[j] 时： mm 一定在 右排序数组 中，即旋转点 xx 一定在[i, m][i,m] 闭区间内，因此执行 j = mj=m；
  • 当 nums[m] = nums[j]nums[m]=nums[j] 时： 无法判断 mm 在哪个排序数组中，即无法判断旋转点 x 在 [i, m][i,m] 还是 [m + 1, j][m+1,j] 区间中。解决方案： 执行 j = j - 1j=j−1 缩小判断范围，分析见下文。
• 返回值： 当 i = j，i=j 时跳出二分循环，并返回 旋转点的值 nums[i]nums[i] 即可。

其他证明参照🔗

/**
         * 二分法
         *
         * @param numbers
         * @return
         */
public int minArray(int[] numbers) {
    int left = 0;
    int right = numbers.length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (numbers[mid] > numbers[right]) {
            left = mid + 1;
        } else if (numbers[mid] < numbers[right]) {
            right = mid;
        } else if (numbers[mid] == numbers[right]) {
            // right = right - 1;
            // 也可以用线性查找代替二分查找
            int x = left;
            for (int i = left + 1; i < right; i++) {
                if (numbers[i] < numbers[x]) x = i;
            }
            return numbers[x];
        }
    }
    return numbers[left];
}