题目描述

解题思路

暴力法

由于正方形的面积等于边长的平方，因此要找到最大正方形的面积，首先需要找到最大正方形的边长，然后计算最大边长的平方即可。
暴力法是最简单直观的做法，具体做法如下：
遍历矩阵中的每个元素，每次遇到 11，则将该元素作为正方形的左上角；
确定正方形的左上角后，根据左上角所在的行和列计算可能的最大正方形的边长（正方形的范围不能超出矩阵的行数和列数），在该边长范围内寻找只包含 1 的最大正方形；
每次在下方新增一行以及在右方新增一列，判断新增的行和列是否满足所有元素都是 1。

// 暴力法
public int maximalSquare(char[][] matrix) {
    int maxSide = 0;
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
        return maxSide;
    }
    for (int i = 0; i < matrix.length; i++) {
        for (int j = 0; j < matrix[0].length; j++) {
            if (matrix[i][j] == '1') {
                // 将1作为左上角，开始搜索正方形
                maxSide = Math.max(maxSide, 1);
                // 计算可能搜索的最大边界，防止越界
                int maxLength = Math.min(matrix.length - i, matrix[0].length - j);
                for (int k = 0; k < maxLength; k++) {
                    // 表示现在是否符合正方形
                    // 判断新增的一行一列是否均为 1
                    boolean flag = true;
                    // 对角不为1，不需要搜索了
                    if (matrix[i + k][j + k] == '0') break;
                    for (int l = 0; l < k; l++) {
                        if (matrix[i + l][j + k] == '0' || matrix[i + k][j + l] == '0') {
                            // 不满足设置标志为false
                            flag = false;
                            break;
                        }
                    }
                    if (flag) {
                        // 更新最大边
                        maxSide = Math.max(k + 1, maxSide);
                    } else break;
                }
            }
        }
    }
    return maxSide * maxSide;
}

dp

先来阐述简单共识

• 若形成正方形（非单 1），以当前为右下角的视角看，则需要：当前格、上、左、左上都是 1
• 可以换个角度：当前格、上、左、左上都不能受 0 的限制，才能成为正方形

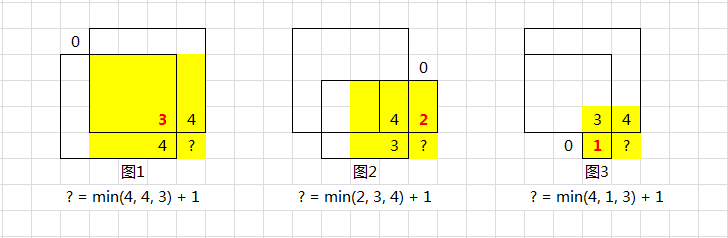
这张图直接展示了当前位置的正方形边长和上，左，左上的关系，也就是取最小的加一。

dp表示的是边长，不是面积，表示面积很难求和这三者的关系。

public int maximalSquare(char[][] matrix) {
    int maxSide = 0;
    if (matrix.length == 0 || matrix[0].length == 0 || matrix == null) return maxSide;
    // dp[i]表示：当前以i为矩形的最大边长
    int[][] dp = new int[matrix.length + 1][matrix[0].length + 1];
    // 初始化都为0
    for (int i = 1; i <= matrix.length; i++) {
        for (int j = 1; j <= matrix[0].length; j++) {
            if (matrix[i - 1][j - 1] == '1') {
                // 三者取最大
                dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
                maxSide = Math.max(maxSide, dp[i][j]);
            }
        }
    }
    return maxSide * maxSide;
}

优化

// 优化
public int maximalSquare(char[][] matrix) {
    int maxSide = 0;
    if (matrix.length == 0 || matrix[0].length == 0 || matrix == null) return maxSide;
    // dp[i]表示：当前以i为矩形的最大边长
    int[] dp = new int[matrix[0].length + 1];
    // 初始化都为0
    for (int i = 1; i <= matrix.length; i++) {
        int northwest = 0;
        for (int j = 1; j <= matrix[0].length; j++) {
            int nextNorthwest = dp[j];
            if (matrix[i - 1][j - 1] == '1') {
                // 三者取最大
                dp[j] = Math.min(dp[j], Math.min(dp[j - 1], northwest)) + 1;
                maxSide = Math.max(maxSide, dp[j]);
            }else dp[j] = 0;
            northwest = nextNorthwest;
        }
    }
    return maxSide * maxSide;
}