题目描述

解题思路

排序做法

可以将数组排序之后，其中的区间不一样的地方就是最短无序的数组。

此时我们要找到该区间的左右边界，因为在这个区间中间可能还有顺序未改变的情况，所以要从左向右昭最小边界，从右向左找最大边界。

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        // 如果本来就是升序
        if (isSort(nums)) return 0;
        // 拷贝数组
        int[] temp = new int[nums.length];
        for (int i = 0; i < nums.length; i++) {
            temp[i] = nums[i];
        }
        // 可以使用
        // System.arraycopy(nums, 0, temp, 0, nums.length);
        // 找到排序后的左右不相等的边界
        int left = 0, right = nums.length - 1;
        Arrays.sort(temp);
        while (temp[left] == nums[left]) {
            left++;
        }
        while (temp[right] == nums[right]) {
            right--;
        }
        return right - left + 1;
    }
    public boolean isSort(int[] nums) {
        for (int i = 1; i < nums.length; i++) {
            if (nums[i - 1] > nums[i]) return false;
        }
        return true;
    }
}

一次遍历

我们可以假设把这个数组分成三段，左段和右段是标准的升序数组，中段数组虽是无序的，但满足最小值大于左段的最大值，最大值小于右段的最小值。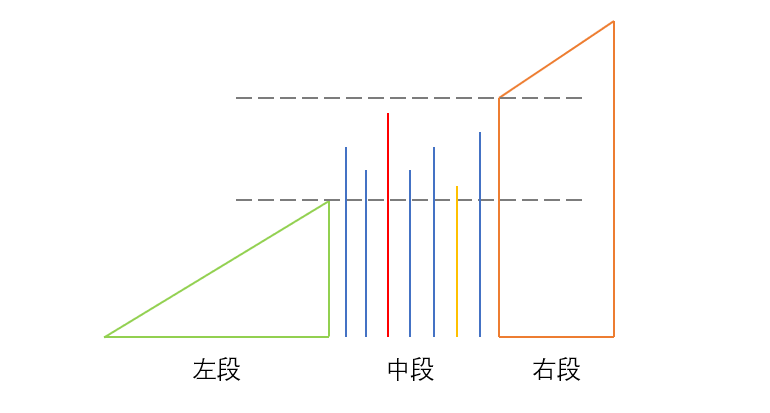

那么我们目标就很明确了，找中段的左右边界，我们分别定义为begin 和 end;
分两头开始遍历:
从左到右维护一个最大值max,在进入右段之前，那么遍历到的nums[i]都是小于max的，我们要求的end就是遍历中最后一个小于max元素的位置；
同理，从右到左维护一个最小值min，在进入左段之前，那么遍历到的nums[i]也都是大于min的，要求的begin也就是最后一个大于min元素的位置。

注意找最左边界和最右边界的方法，右端所有数都大于中间区间最大值，左端所有值都小于中间区间最小值。所以小于max就更新索引，大于min就更新索引。

// 一次遍历
public int findUnsortedSubarray(int[] nums) {
    int len = nums.length;
    int max = nums[0];
    int min = nums[len - 1];
    // right初始化为-1，本来就是升序的情况，返回0
    int left = 0, right = len - 1;
    for (int i = 0; i < len; i++) {
        if (nums[i] < max) right = i;
        else max = nums[i];
        if (nums[len - i - 1] > min) left = len - i - 1;
        else min = nums[len - i - 1];
    }
    return right - left + 1;
}