二分查找
- 方法一
- 方法二
- 相关题目
  - 搜索插入位置
    - 力扣链接）">题目描述：（力扣链接）
    - 解题方法
      - 方法一:
      - 方法二
  - 在排序数组中查找元素的第一个和最后一个位置
    - 力扣链接）">题目描述：（力扣链接）
    - 解题方法
  - X的平方根
    - 力扣链接）">题目描述（力扣链接）
    - 解题方法：
  - 有效的完全平方数
    - 力扣链接）">题目描述（力扣链接）
    - 解题方法:
- 33. 搜索旋转排序数组">33. 搜索旋转排序数组
  - 题目描述
  - 解题思路

二分查找

前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

以经典题为例：

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。力扣链接

示例：

输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4

方法一

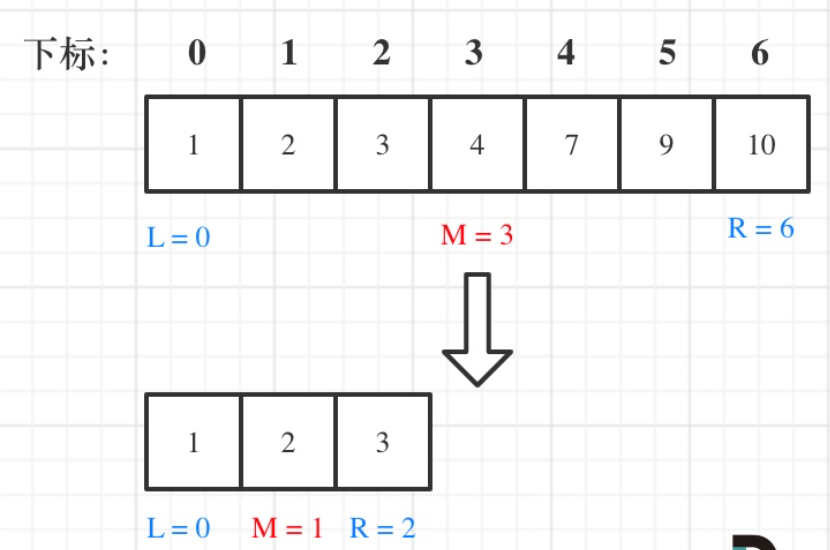
定义target在左闭右闭的区间中，即[left,right]。

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

示意图：

二分查找 - 图3

代码：

class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        // 判断是否小于最小和大于最大
        if(target < nums[0] || target > nums[right]) {
            return -1;
        }
        // 左边界小于等于右边界
        while(left <= right) {
            int middle = (left + right) / 2;
            // 相等直接输出
            if(target == nums[middle]) {
                return middle;
            }
            // 小于则将右边界收缩
            else if(target < nums[middle]) {
                right = middle - 1;
            }
            // 大于则将右边界收缩
            else if(target > nums[middle]) {
                left = middle + 1;
            }
        }
        return -1;
    }
}

方法二

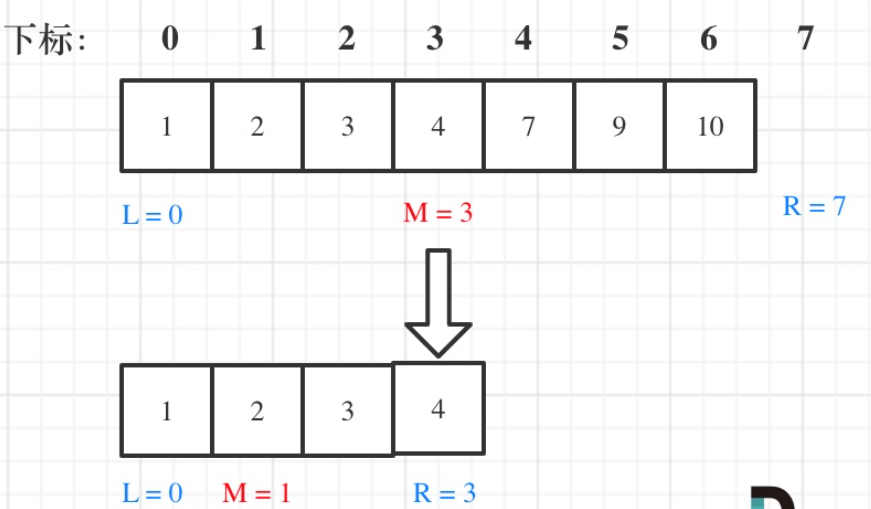
定义target在左闭右开的区间中，即[left,right]。

while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

示意图：

二分查找 - 图4

代码：

class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length;
        // 判断是否小于最小和大于最大
        if(target < nums[0] || target > nums[right-1]) {
            return -1;
        }
        // 左边界小于右边界
        while(left < right) {
            int middle = (left + right) / 2;
            // 相等直接输出
            if(target == nums[middle]) {
                return middle;
            }
            // 小于则将右边界收缩
            else if(target < nums[middle]) {
                right = middle;     // 此时边界需要为[middle,right)
            }
            // 大于则将右边界收缩
            else if(target > nums[middle]) {
                left = middle + 1;  // 此时边界需要为[middle+1,right)
            }
        }
        return -1;
    }
}

注意：在left，right都为Integer.MAX_VALUE时会造成越界，所以可以使用int mid = left + ((right - left) / 2);代替 int middle = (left + right) / 2;

相关题目

搜索插入位置

题目描述：（力扣链接）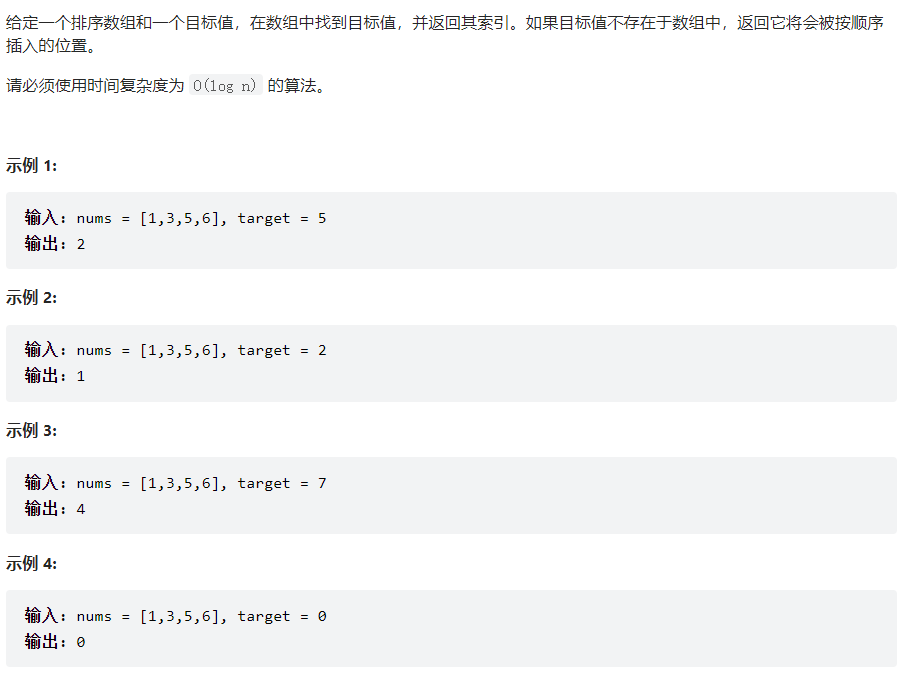

解题方法

解题流程：carl哥的解题流程

贴上代码：

方法一:

自己使用的时左闭右闭的写法，此处有四种情况:

目标值在数组中
目标值在数组的范围
目标值在数组范围的右侧
目标值在数组范围的左侧

此处先使用经典的二分查找的方法，可以先判断出第一种情况，最后返回值为right + 1（注意此处包括了三种情况）

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0,right = nums.length - 1;
        // 循环判断
        while(left <= right) {
            int middle = (right + left) / 2;
            if(target == nums[middle]) {
                return middle;
            }
            else if(target < nums[middle]) {
                right = middle - 1;
            }
            else if(target > nums[middle]) {
                left = middle + 1;
            }
        }
        // 返回情况
        // 目标值在所有数组的后面right + 1
        // 目标值在数组中 middle
        // 目标值在数组前，
        // 此时经过循环之后，right在等于0时也会循环一次，所以最终循环之后right的结果为-1
        return right + 1;
    }
}

方法二

暴力解法

int searchInsert(vector<int>& nums, int target) {
        for (int i = 0; i < nums.size(); i++) {
        // 分别处理如下三种情况
        // 目标值在数组所有元素之前
        // 目标值等于数组中某一个元素
        // 目标值插入数组中的位置
            if (nums[i] >= target) { // 一旦发现大于或者等于target的num[i]，那么i就是我们要的结果
                return i;
            }
        }
        // 目标值在数组所有元素之后的情况
        return nums.size(); // 如果target是最大的，或者 nums为空，则返回nums的长度
    }

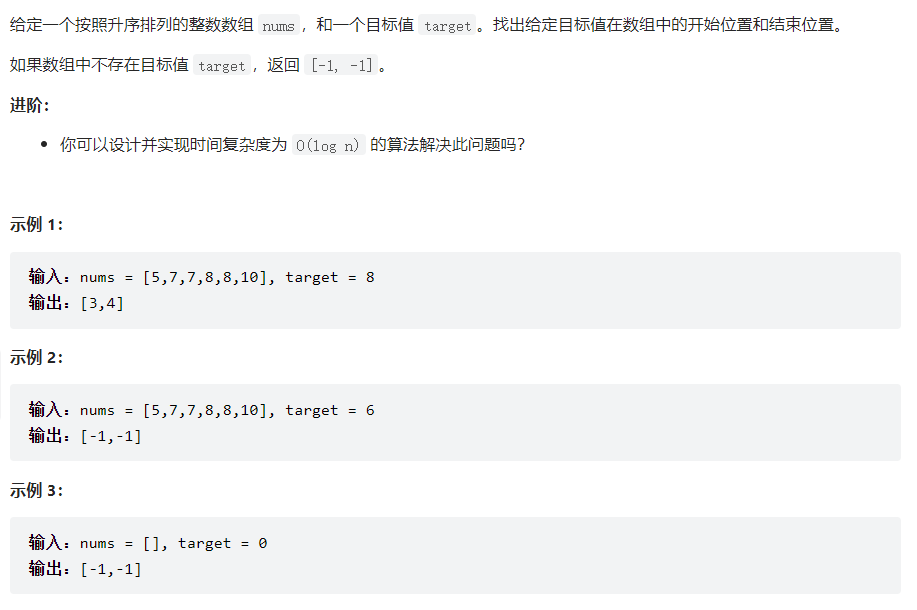
在排序数组中查找元素的第一个和最后一个位置

题目描述：（力扣链接）

二分查找 - 图6

解题方法

解题流程：carl哥的解题流程

此处也有三种情况

情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5},target为6，此时应该返回{-1, -1}
情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int rightBorder = getRightBorder(nums, target);
        int leftBorder = getLeftBorder(nums, target);
        // 数字值范围超过数组,就是左边界在右边或者有边界在左边
        // 情况二
        if(rightBorder == -2 || leftBorder == -2) return new int[]{-1, -1};
        // 情况一
        if(rightBorder - leftBorder > 1) return new int[]{leftBorder + 1, rightBorder - 1};    // 此处最后算出的right和left多减了一和多加了一
        // 情况三
        return new int[]{-1, -1};
        // 数字范围在数组中，但数组中无此值
    }
    public static int getRightBorder(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        int rightBorder = -2;
        // 寻找右边界
        while (left <= right) {
            int middle = (right + left) / 2;
            if(target < nums[middle]) {
                right = middle - 1;
            }else {     // 当target==nums[middle]时，此时将left等于middle+1 
                left = middle + 1;
                rightBorder = left; // 将left作为右边界
            }
        }
        return rightBorder;
    }
    public static int getLeftBorder(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        int leftBorder = -2;
        // 寻找左边界
        while (left <= right) {
            int middle = (right + left) / 2;
            if(target <= nums[middle]) {
                right = middle - 1;     // 当target==nums[middle]时，此时将right等于middle+1 
                leftBorder = right;     // 将right作为左边界
            }else {   
                left = middle + 1;
            }
        }
        return leftBorder;
    }
}

X的平方根

题目描述（力扣链接）

二分查找 - 图7

解题方法：

此处也可以使用二分法，注意最后需要返回right，当middle平方等于x时直接返回，若没有等于，需要返回前一个值，此时right在最后被减了一，所以直接返回right即可。

 public static int mySqrt(int x) {
        // 判断为0，1时直接返回
        if (x == 0 || x == 1) {
            return x;
        }
        int left = 1;
        int right = x / 2;  // 直接将right赋值为x的二分之一，减少计算
        while (left <= right) {
            int middle = (right + left) / 2;
            // 使用除法代替乘法，防止使用乘法溢出
            if (middle == (x/middle)) {
                return middle;
            }
            else if (middle > (x / middle)) {
                right = middle - 1;
            }
            else if (middle < (x / middle)) {
                left = middle + 1;
            }
        }
        return right;
    }

有效的完全平方数

题目描述（力扣链接）

二分查找 - 图8

解题方法:

与上一题一致，但注意此处范围过大，需要使用long类型。right也可以从num/2开始查找，但是注意判断num==1的情况。

class Solution {
    public boolean isPerfectSquare(int num) {
        // 数据过大，使用long类型
        long left = 1;
        long right = num;
        while(left <= right) {
            long middle = (right + left) / 2;
            if(middle*middle == num) {
                return true;
            }
            else if(middle*middle < num) {
                left = middle + 1;
            }
            else if(middle*middle > num) {
                right = middle - 1;
            }
        }
        return false;
    }
}

33. 搜索旋转排序数组

题目描述

解题思路

https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/sou-suo-xuan-zhuan-pai-xu-shu-zu-by-leetcode-solut/
注意要求的时间复杂度为O(log n)，所以可以使用二分法。
但是直接使用二分不行，因为中间不是升序的。所以需要进行判断：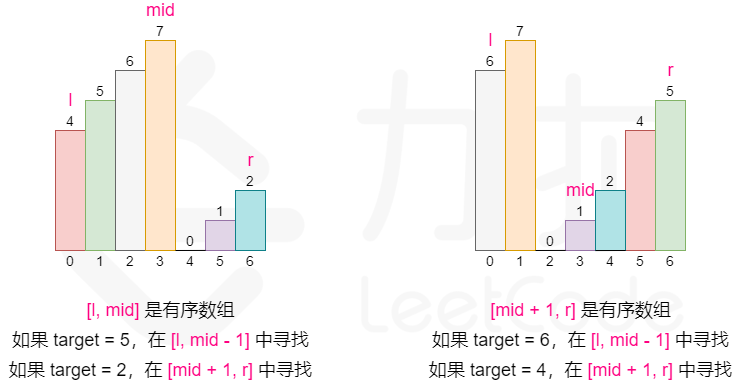

public int search(int[] nums, int target) {
    int n = nums.length;
    if (n == 0) return 0;
    if (n == 1) return nums[0] == target ? 0 : -1;
    int l = 0, r = n - 1;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (nums[mid] == target) return mid;
        // 左边有序
        if (nums[0] <= nums[mid]) {
            if (nums[0] <= target && target <= nums[mid]) {
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        } else {
            if (nums[mid] <= target && target <= nums[n - 1]) {
                l = mid + 1;
            }else {
                r = mid - 1;
            }
        }
    }
    return -1;
}