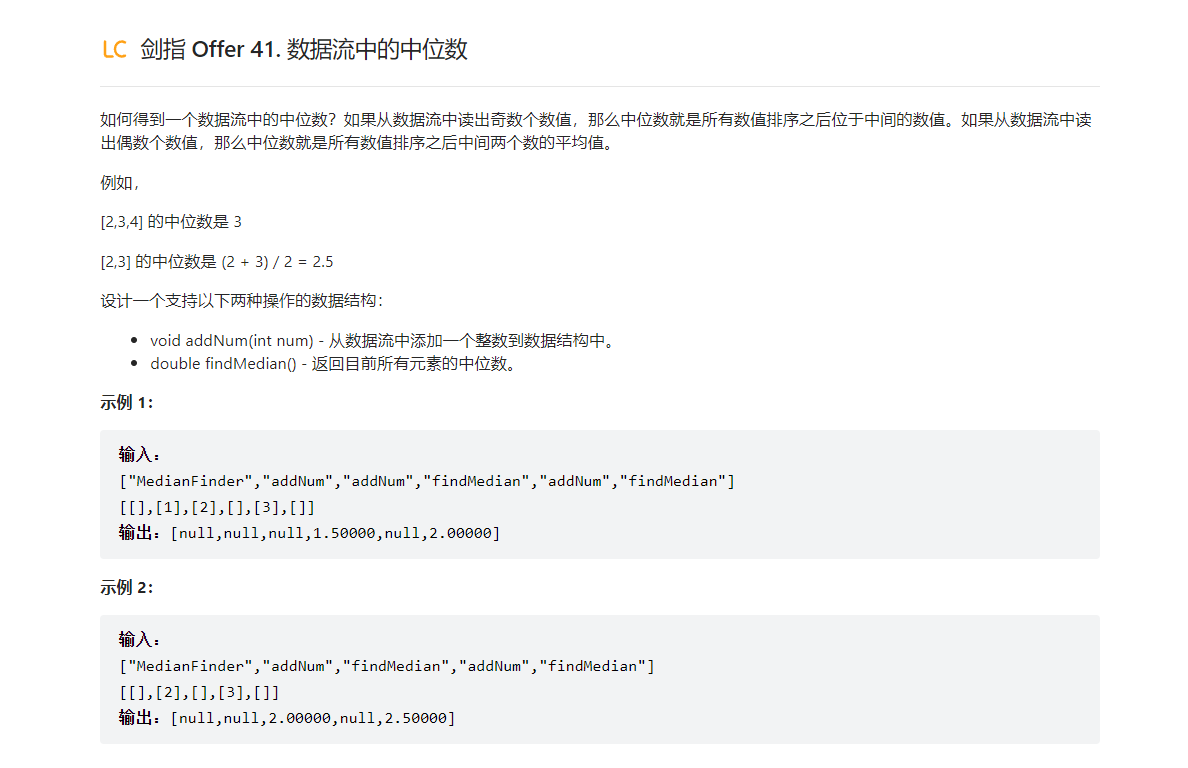
题目描述

image.png

解题思路

使用排序超时。。。
针对本题，根据以上思路，可以将数据流保存在一个列表中，并在添加元素时 保持数组有序 。此方法的时间复杂度为 O(N) ，其中包括： 查找元素插入位置 O(logN) （二分查找）、向数组某位置插入元素 O(N) （插入位置之后的元素都需要向后移动一位）。
借助 堆 可进一步优化时间复杂度。

借助堆可进一步优化时间复杂度。

建立一个小顶堆A和大顶堆B，各保存列表的一半元素，且规定:

  • A保存较大的一半，长度为N / 2(N为偶数)或(N + 1) / 2(N为奇数);
  • B保存较小的一半，长度为N / 2(N为偶数)或(N + 1) / 2 (N为奇数);

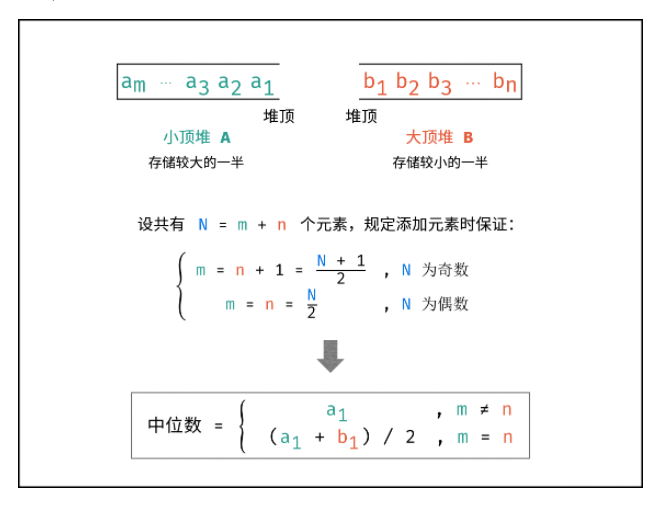
image.png
算法流程：
addNum(num)函数:

  • 如果两个堆的大小不相等，表示此时所有数组的长度是奇数。需要向B中插入元素，但为了保证所有的数字都有序，所以需要先在A中插入，排好序后再在B中插入。
  • 如果两个堆大小相等，那么插入A，流程也是需要先插入B，再插入A。

    假设插入数字 num= 遇到情况 1. 。由于 num 可能属于 “较小的一半” （即属于 B ），因此不能将 nums 直接插入至 A 。而应先将 num 插入至 B ，再将 B 堆顶元素插入至 A 。这样就可以始终保持 A 保存较大一半、 B 保存较小一半。

findMedian() 函数：

  • 如果两个堆的大小不相等，表示此时所有数组的长度是奇数。取出A的队头，注意是A，因为在偶数的时候我们插入了A，所以变成了奇数，取就要从A中取。

  • 如果两个堆相等，那么就是偶数，两个堆都取出元素，求平均值即可。

    代码

    ```java class MedianFinder { /**

    1.    * 大顶堆和小顶堆实现
    2.    */

    Queue A, B;

    public MedianFinder() {

    1.   A = new PriorityQueue<>();  // 小顶堆，存储较大的一半的值
    2.   B = new PriorityQueue<>((x, y) -> y - x);   // 大顶堆，存储较小的一半

    }

    public void addNum(int num) {

    1.   if (A.size() != B.size()) {
    2.       // 如果两个堆的大小不相等，那么此时就为奇数
    3.       // 先将num入A，排好序后，取出A中最小的，再入B
    4.       A.add(num);
    5.       B.add(A.poll());
    6.   } else {
    7.       // 如果两个堆的大小不相等，那么此时就为偶数
    8.       // 与上相反
    9.       B.add(num);
    10.       A.add(B.poll());
    11.   }

    }

    public double findMedian() {

    1.   // 注意此时不能使用poll，poll出队列之后，后面就乱序了
    2.   return A.size() == B.size() ? (A.peek() + B.peek()) / 2.0 : A.peek();

    }

} ```