题目描述

解题思路

本题注意区分多重背包和0-1背包。
本题可以抽象为2个背包，0的个数和1的个数分别代表2个维度的背包。

• 确定dp数组（dp table）以及下标的含义

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

• 确定递推公式

dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
zeroNum和oneNum代表重量，而value表示则是字符串本身的个数。

• dp数组如何初始化

因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖。

• 确定遍历顺序

两个维度遍历，但是背包遍历还是要按照倒序遍历

• 举例推导dp数组

以输入：[“10”,”0001”,”111001”,”1”,”0”]，m = 3，n = 3为例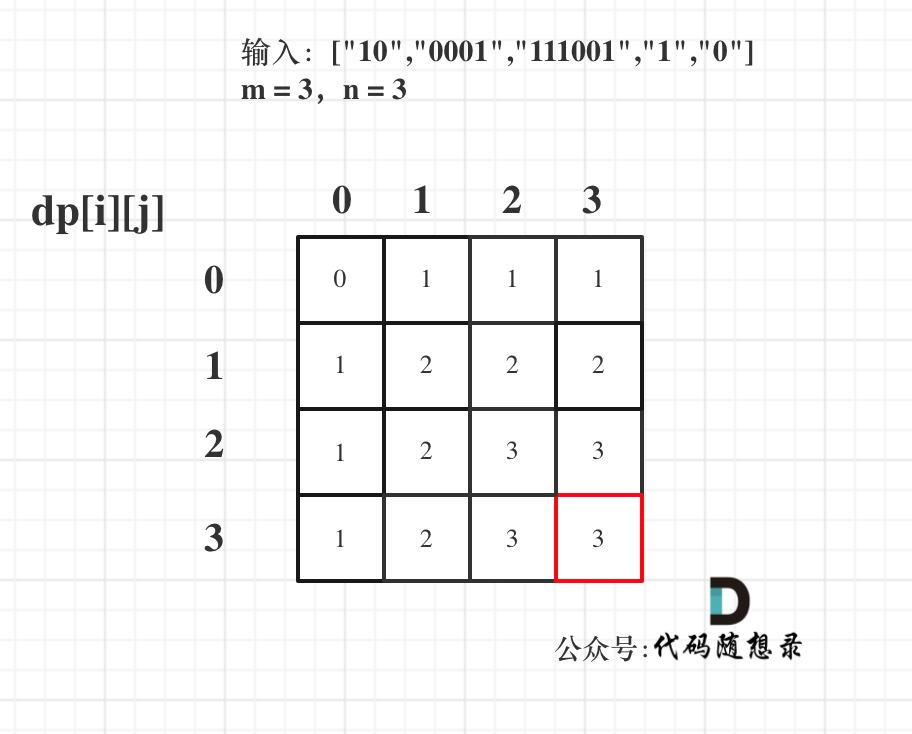

public int findMaxForm(String[] strs, int m, int n) {
    int[][] dp = new int[m + 1][n + 1];
    // 遍历物品
    for (String str : strs) {
        char[] chars = str.toCharArray();
        int zeroNum = 0, oneNums = 0;
        for (int i = 0; i < chars.length; i++) {
            if (chars[i] == '1') {
                oneNums++;
            } else {
                zeroNum++;
            }
        }
        // 遍历2个背包
        for (int i = m; i >= zeroNum; i--) {
            for (int j = n; j >= oneNums; j--) {
                dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNums] + 1);
            }
        }
    }
    return dp[m][n];
}