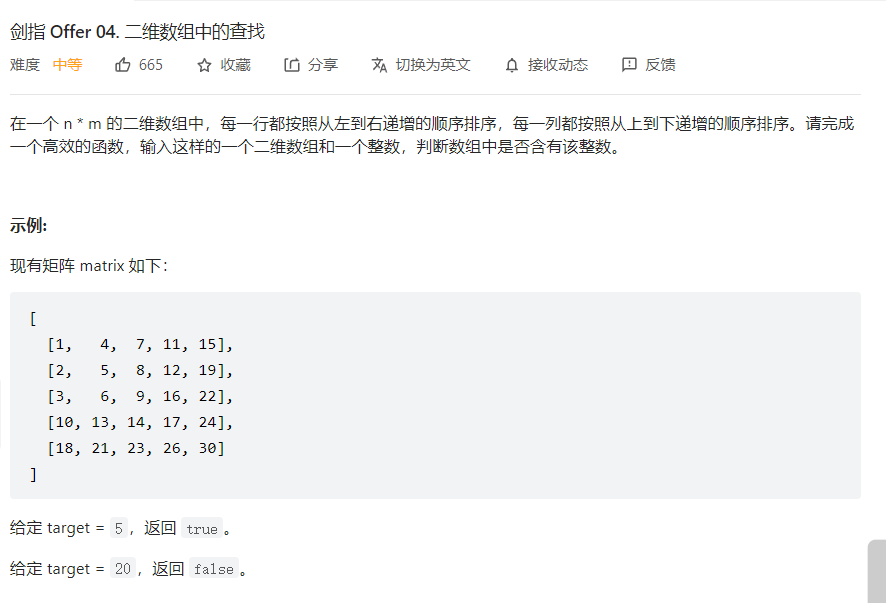
题目描述

方法一

二分查找（时间复杂度O(m * log n)）

   /**
         * 二分查找
         *
         * @param array
         * @param target
         * @return
         */
        public boolean twoSearch(int[] array, int target) {
            int left = 0;
            int right = array.length - 1;
            while (left <= right) {
                int mid = (left + right) / 2;
                if (array[mid] > target) {
                    right = mid - 1;
                } else if (array[mid] < target) {
                    left = mid + 1;
                } else if (array[mid] == target) {
                    return true;
                }
            }
            return false;
        }

方法二

如下图所示，我们将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于 二叉搜索树 ，即对于每个元素，其左分支元素更小、右分支元素更大。因此，通过从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。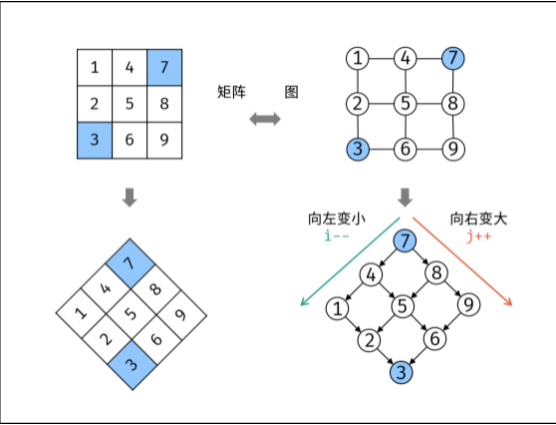

根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素，本文称之为 标志数 ，以 matrix 中的 左下角元素 为标志数 flag ，则有:
若 flag > target ，则 target 一定在 flag 所在 行的上方 ，即 flag 所在行可被消去。
若 flag < target ，则 target 一定在 flag 所在 列的右方 ，即 flag 所在列可被消去。

算法流程：
从矩阵 matrix 左下角元素（索引设为 (i, j) ）开始遍历，并与目标值对比：

• 当 matrix[i][j] > target 时，执行 i— ，即消去第 i 行元素；
• 当 matrix[i][j] < target 时，执行 j++ ，即消去第 j 列元素；
• 当 matrix[i][j] = target 时，返回 truetrue ，代表找到目标值。

若行索引或列索引越界，则代表矩阵中无目标值，返回 falsefalse 。
每轮 i 或 j 移动后，相当于生成了“消去一行（列）的新矩阵”， 索引(i,j) 指向新矩阵的左下角元素（标志数），因此可重复使用以上性质消去行（列）。

复杂度分析：
时间复杂度 O(M+N)O(M+N) ：其中，NN 和 MM 分别为矩阵行数和列数，此算法最多循环 M+NM+N 次。
空间复杂度 O(1)O(1) : i, j 指针使用常数大小额外空间。

/**
 * 标志数法
 *
 * @param matrix
 * @param target
 * @return
 */
public boolean findNumberIn2DArray(int[][] matrix, int target) {
    // 找到左下角的标志数
    int i = matrix.length - 1;
    int j = 0;
    while (i >= 0 && j < matrix[0].length) {
        if (matrix[i][j] < target) j++;
        else if (matrix[i][j] > target) i--;
        else return true;
    }
    return false;
}