在对相邻的2个元素需要进行匹配的时候，那么此时就可以利用栈的先进先出来进行实现。

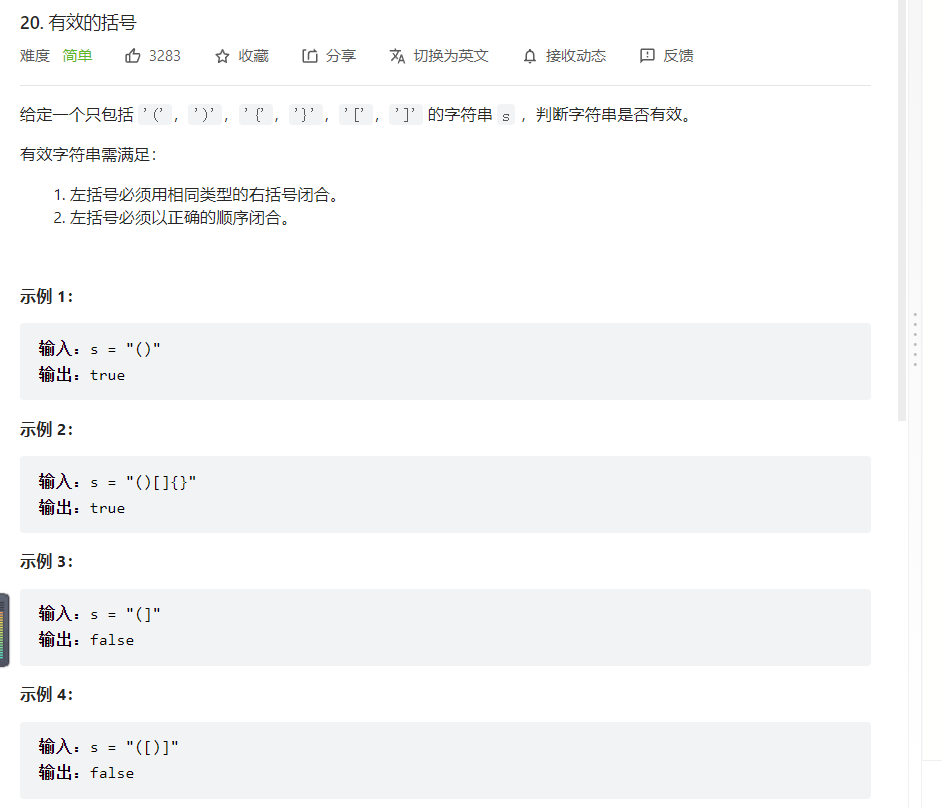
20. 有效的括号

题目描述

解题思路

• 第一种情况：已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false
• 第二种情况：遍历字符串匹配的过程中，发现栈里没有要匹配的字符。所以return false
• 第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号return false

• 那么什么时候说明左括号和右括号全都匹配了呢，就是字符串遍历完之后，栈是空的，就说明全都匹配了。 ```java /**

     * 正常的放入
     *
     * @param s
     * @return
     */

  public boolean isValid(String s) { Stack stack = new Stack<>(); char ch; for (int i = 0; i < s.length(); i++) {

    ch = s.charAt(i);
    if (ch == '(') {
        stack.push('(');
    } else if (ch == '{') {
        stack.push('{');
    } else if (ch == '[') {
        stack.push('[');
    } else if (stack.isEmpty()) {
        // 此时栈中为空，右括号过多
        return false;
    } else if (stack.peek() == '(' && ch == ')' || stack.peek() == '{' && ch == '}' || stack.peek() == '[' && ch == ']') {
        stack.pop();
    } else {
        // 和栈顶元素不匹配的情况
        return false;
    }

  }

  // 遍历完后，栈中不为空，此时左括号过多 return stack.isEmpty(); }

/**

     * 放入相反的括号，更加方便
     *
     * @param s
     * @return
     */

public boolean isValid(String s) { Stack stack = new Stack<>(); char ch; for (int i = 0; i < s.length(); i++) { ch = s.charAt(i); if (ch == ‘(‘) { // 放入相反的括号 stack.push(‘)’); } else if (ch == ‘{‘) { stack.push(‘}’); } else if (ch == ‘[‘) { stack.push(‘]’); } else if (stack.isEmpty() || stack.peek() != ch) { // 此时栈中为空，右括号过多 // 此时括号不匹配 return false; } else { // 当括号匹配时，出栈 stack.pop(); } }

// 遍历完后，栈中不为空，此时左括号过多
return stack.isEmpty();

}

<a name="VNYaT"></a>
# 1047. 删除字符串中的所有相邻重复项
<a name="GtmZu"></a>
## 题目描述
![image.png](https://cdn.nlark.com/yuque/0/2022/png/26393840/1653917798425-462891f0-9170-404a-ae17-644c4b3b5cdf.png#clientId=u858f267f-173a-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=456&id=u557c8ff5&margin=%5Bobject%20Object%5D&name=image.png&originHeight=570&originWidth=1061&originalType=binary&ratio=1&rotation=0&showTitle=false&size=50638&status=done&style=none&taskId=u153a422c-2d75-49ba-8f7e-f33974956ca&title=&width=848.8)
<a name="R0nDD"></a>
## 解题思路
利用栈的特性即可<br />![](https://cdn.nlark.com/yuque/0/2022/gif/26393840/1653917883202-f4cb9ce8-1884-40be-8c3b-857753e61f63.gif#clientId=u858f267f-173a-4&crop=0&crop=0&crop=1&crop=1&from=paste&id=u27095bdb&margin=%5Bobject%20Object%5D&originHeight=354&originWidth=422&originalType=url&ratio=1&rotation=0&showTitle=false&status=done&style=none&taskId=u63982049-019b-4a50-a59b-da5f18646fc&title=)
```java
        /**
         * 使用栈
         *
         * @param s
         * @return
         */
        public String removeDuplicates(String s) {
            Stack<Character> stack = new Stack<>();
            char ch;
            for (int i = 0; i < s.length(); i++) {
                ch = s.charAt(i);
                if (!stack.isEmpty()) {
                    char temp = stack.peek();
                    // 相等即出栈
                    if (ch == temp) {
                        stack.pop();
                    } else {
                        // 不相等即入栈
                        stack.push(ch);
                    }
                } else {
                    // 栈为空直接入栈
                    stack.push(ch);
                }
            }
            // 将栈转化为字符串
            String str = "";
            while (!stack.isEmpty()) {
                str = stack.pop() + str;
            }
            return String.valueOf(str);
        }
        /**
         * 双指针法
         *
         * @param s
         * @return
         */
        public String removeDuplicates(String s) {
            int fast = 0, slow = 0;
            char[] chars = s.toCharArray();
            while (fast < s.length()) {
                // 直接用fast指针覆盖slow指针的值
                chars[slow] = chars[fast];
                // 存在相邻相等的元素，slow减一，不用减二，slow会被下次循环覆盖
                if (slow > 0 && chars[slow] == chars[slow - 1]) {
                    slow--;
                } else {
                    slow++;
                }
                fast++;
            }
            return String.valueOf(chars, 0, slow);
        }

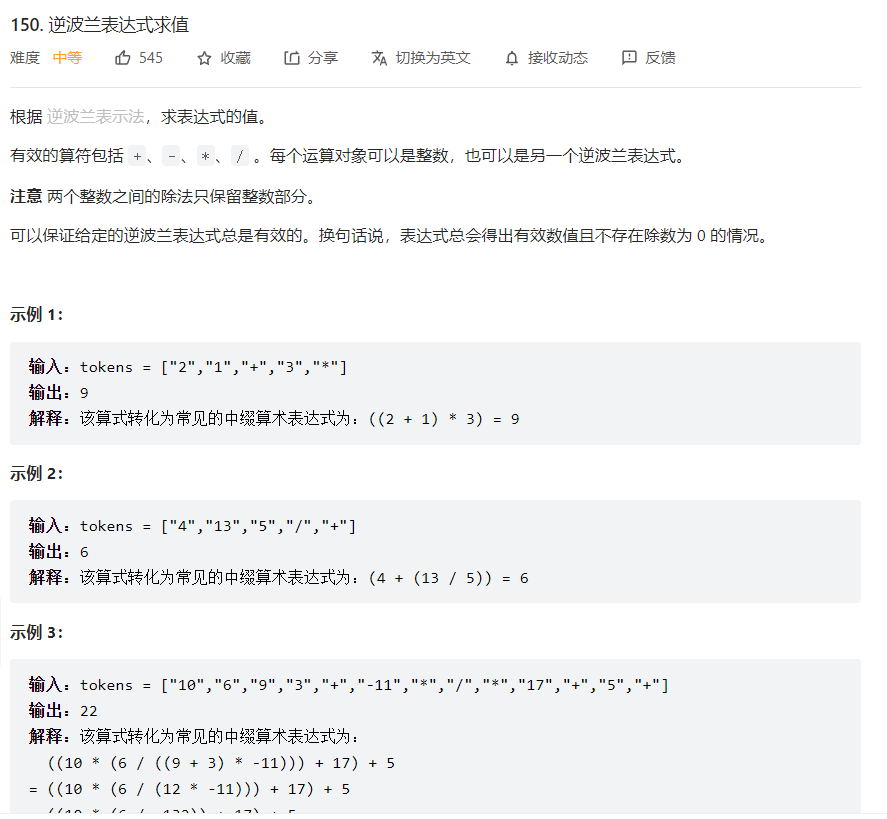
150. 逆波兰表达式求值

题目描述

解题思路

也就是后缀表达式，遇到运算符的话，就取出前面的2个元素运算之后在入栈。知道栈里面最后一个元素就是结果。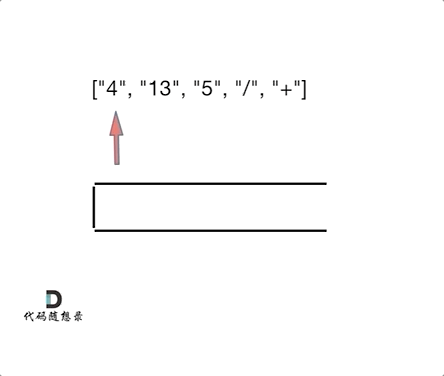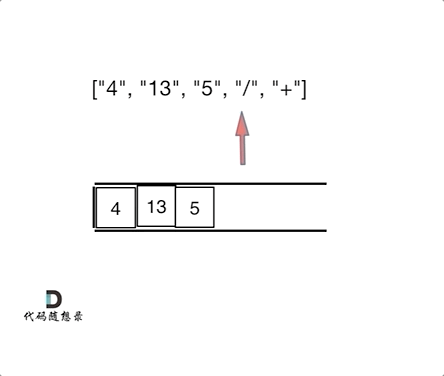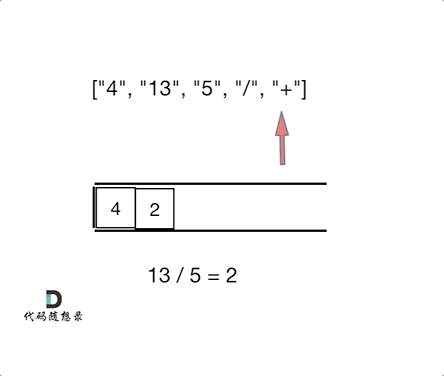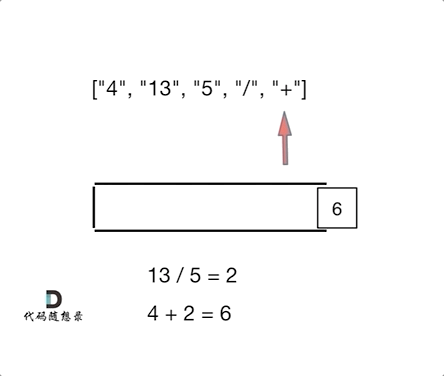

public int evalRPN(String[] tokens) {
    Stack<Integer> stack = new Stack<>();
    int temp1, temp2;
    for (int i = 0; i < tokens.length; i++) {
        // 判断是否为响应的运算符，如果为运算符，即去栈顶上的两个树进行运算
        // 运算后将结果入栈，进行下一次取值
        if (tokens[i].equals("+")) {
            temp1 = stack.pop();
            temp2 = stack.pop();
            stack.push(temp1 + temp2);
        } else if (tokens[i].equals("*")) {
            temp1 = stack.pop();
            temp2 = stack.pop();
            stack.push(temp1 * temp2);
        } else if (tokens[i].equals("/")) {
            temp1 = stack.pop();
            temp2 = stack.pop();
            stack.push(temp2 / temp1);
        } else if (tokens[i].equals("/")) {
            temp1 = stack.pop();
            temp2 = stack.pop();
            stack.push(temp2 - temp1);
        } else {
            stack.push(Integer.valueOf(tokens[i]));
        }
    }
    return stack.pop();
}