题目描述

解题思路

• 确定dp数组（dp table）以及下标的含义

dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。

以后需要求子序列的问题一半都用i表示下标i-1。

• 确定递推公式

根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。
即当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;

• dp数组如何初始化

根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的！
但dp[i][0] 和dp[0][j]要初始值，因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
举个例子A[0]如果和B[0]相同的话，dp[1][1] = dp[0][0] + 1，只有dp[0][0]初始为0，正好符合递推公式逐步累加起来。

• 遍历顺序

先遍历哪个字符串都可以。
每次遍历需要记录dp的最大值。保存最大的字符字串。

• 举例推导dp数组

拿示例1中，A: [1,2,3,2,1]，B: [3,2,1,4,7]为例，画一个dp数组的状态变化，如下：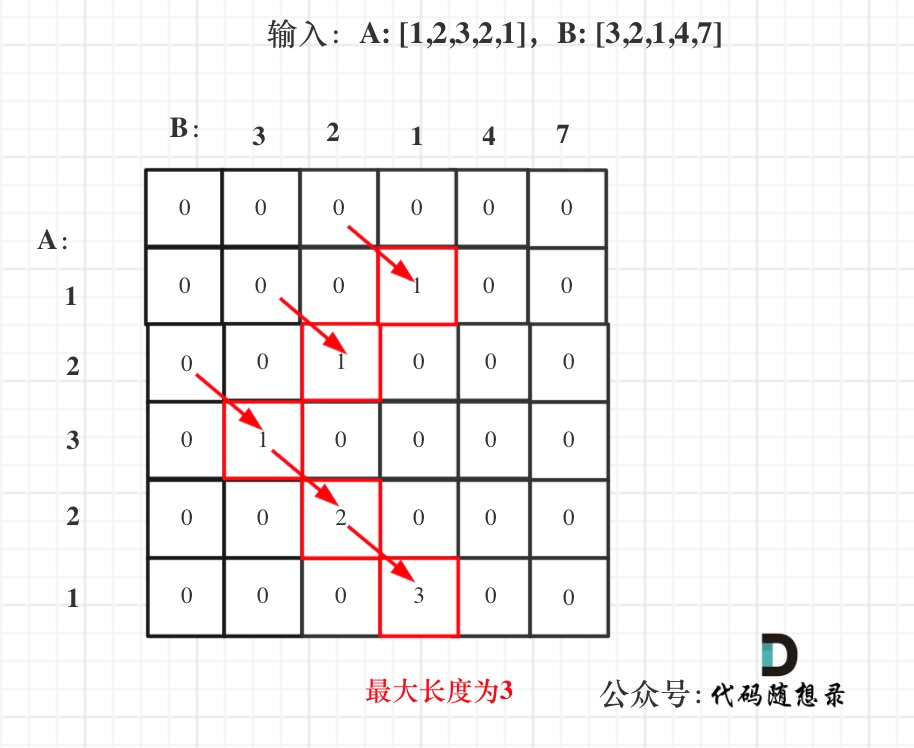

/**
         * 动态规划（二维数组）
         *
         * @param nums1
         * @param nums2
         * @return
         */
public int findLength(int[] nums1, int[] nums2) {
    // dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。
    int[][] dp = new int[nums1.length + 1][nums2.length + 1];
    int result = 0; // 记录最大的重复数组长度
    dp[0][0] = 0;   // 初始化，如果dp[0][0]初始化为1，那么dp[1][1] = dp[0][0] + 1 = 2，此时的下标还是0(1 - 1)，所以不满足题意
    for (int i = 1; i <= nums1.length; i++) {
        for (int j = 1; j <= nums2.length; j++) {
            if (nums1[i] == nums2[j]) { // 如果相等，才是重复的数组
                dp[i][j] = dp[i - 1][j - 1] + 1;    // 等于前一个重复的数字加一
            }
            if (dp[i][j] > result) result = dp[i][j];
        }
    }
    return result;
}

• 时间复杂度：$O(n × m)$，n 为A长度，m为B长度
• 空间复杂度：$O(n × m)$

滚动数组优化

/**
         * 滚动数组
         *
         * @param nums1
         * @param nums2
         * @return
         */
public int findLength(int[] nums1, int[] nums2) {
    int[] dp = new int[nums1.length + 1];
    int result = 0;
    Arrays.fill(dp, 0);
    for (int i = 1; i <= nums1.length; i++) {
        for (int j = nums2.length; j > 0; j--) { // 需要倒的遍历，和背包问题中的滚动数组一致，以免覆盖前面的元素
            if (nums1[i - 1] == nums2[j - 1]) {
                dp[j] = dp[j - 1] + 1;
            } else {
                dp[j] = 0;  // 赋值为0
            }
            if (dp[j] > result) result = dp[j];
        }
    }
    return result;
}