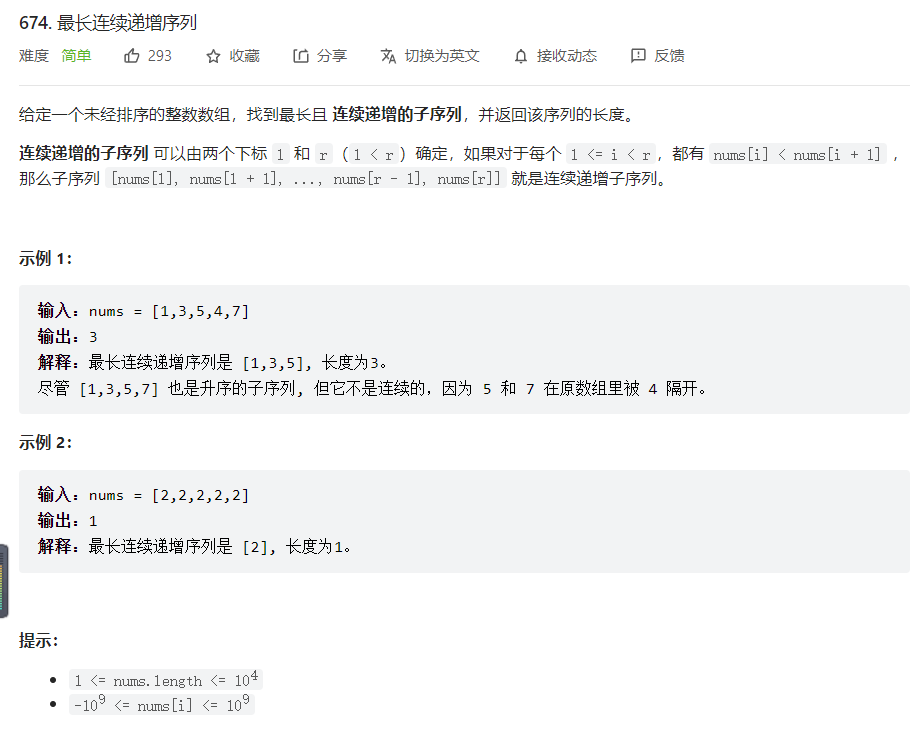
题目描述

解题思路

DP

本题和最长递增子序列的区别就是递推公式！！！
如果 nums[i + 1] > nums[i]，那么以 i+1 为结尾的数组的连续递增的子序列长度 一定等于 以i为结尾的数组的连续递增的子序列长度 + 1 。即：dp[i + 1] = dp[i] + 1;
遍历顺序也只是用一个for来遍历，因为求得是连续的递增子序列，所以只需要判断 i 和 i - 1 即可。

// 动态规划  O(n * n)
// 和lc的300题递增子序列相差不大，300题是没有连载一起，需要在使用一个for循环判断
public int findLengthOfLCIS(int[] nums) {
    if (nums.length == 1) {
        return 1;
    }
    int[] dp = new int[nums.length];
    int result = 0;
    Arrays.fill(dp, 1);
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] > nums[i - 1]) {
            dp[i] = Math.max(dp[i], dp[i - 1] + 1);
        }
        if (dp[i] > result) result = dp[i];
    }
    return result;
}

贪心

这道题目也可以用贪心来做，也就是遇到nums[i + 1] > nums[i]的情况，count就++，否则count为1，记录count的最大值就可以了。

// 贪心   O(n)
// 如果i大于i-1,count++，否则count重置
public int findLengthOfLCIS(int[] nums) {
    if (nums.length == 1) {
        return 1;
    }
    int count = 1;  // 最小连续为1
    int result = 1;
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] > nums[i - 1]) {
            count++;
        } else {
            result = Math.max(result, count);
            count = 1;
        }
        result = Math.max(result, count);
    }
    return result;
}