题目描述

解题思路

dp

• 确定dp含义

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

• 递推公式

当i索引的字符和j索引的字符相同时，i，j区间是否为回文串的几种情况：

• i==j时，例如a，是回文串
• j - i == 1 时，例如aa，是回文串
• 如果j - i > 1，此时需要根据i + 1 和 j - 1是否为回文字串推出，所以dp[i][j] = dp[i+1][j-1];

当i索引的字符和j索引的字符不相同时，不是回文串。

• dp数组如何初始化

dp[i][j]可以初始化为true么？ 当然不行，怎能刚开始就全都匹配上了。
所以dp[i][j]初始化为false。

• 遍历顺序

首先从递推公式中可以看出，情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。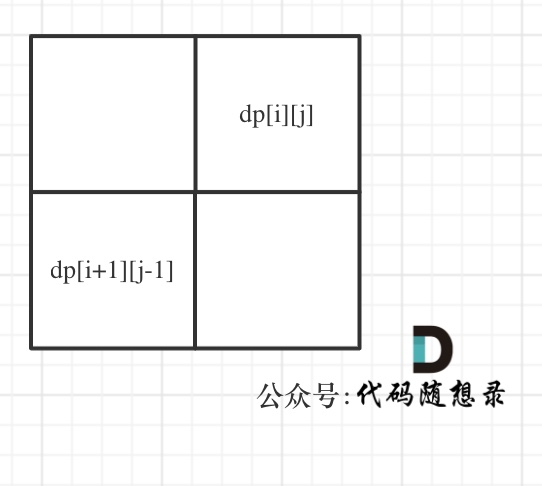

此时需要使用左下角的数才能推出右上角的数，所以一定注意是从下到上，从左到右遍历。

• 举例推导dp数组

举例，输入：”aaa”，dp[i][j]状态如下：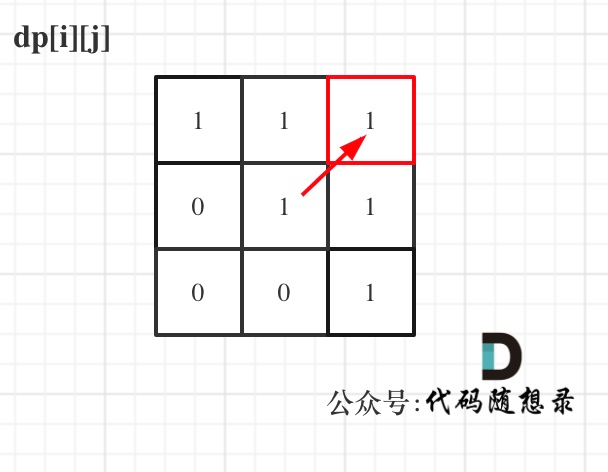

注意因为dp[i][j]的定义，所以j一定是大于等于i的，那么在填充dp[i][j]的时候一定是只填充右上半部分。

/**
         * 动态规划
         *
         * @param s
         * @return
         */
public int countSubstrings(String s) {
    // 表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。
    boolean[][] dp = new boolean[s.length()][s.length()];
    char[] array = s.toCharArray();
    int result = 0; // 回文字串个数
    // 初始化，最开始一定不是回文字串
    for (int i = 0; i < s.length(); i++) {
        dp[0][i] = false;
        dp[i][0] = false;
    }
    // 从下到上，从左到右遍历
    for (int i = array.length - 1; i >= 0; i--) {
        for (int j = i; j < array.length; j++) {
            if (array[i] == array[j]) {
                if (j - i <= 1) {   // 情况一：i=j，只有一个字母，a，为回文字串 情况二：两个字母，aa，也为回文子串
                    result++;
                    dp[i][j] = true;
                } else if (dp[i + 1][j - 1]) { // 情况三：此时大于三个字符，就需要判断中间的区间内是否为回文字串
                    result++;
                    dp[i][j] = true;
                }
            }
        }
    }
    return result;
}

双指针法

大致思路：双指针如何比较回文数，从中间开始，向两边扩散，如果两边值相等，那么就是回文字串。此时，如何判断中心点，例如aabbaa，此时使用1作为中心点就会丢失部分回文串，所以应该使用2作为中心点，那为什么不使用3呢，因为3可以由1扩散得到。
首先确定回文串，就是找中心然后向两边扩散看是不是对称的就可以了。
在遍历中心点的时候，要注意中心点有两种情况。
一个元素可以作为中心点，两个元素也可以作为中心点。
那么有人同学问了，三个元素还可以做中心点呢。其实三个元素就可以由一个元素左右添加元素得到，四个元素则可以由两个元素左右添加元素得到。

/**
         * 双指针法
         *
         * @param s
         * @return
         */
public int countSubstrings(String s) {
    //            首先确定回文串，就是找中心然后向两边扩散看是不是对称的就可以了。
    //            在遍历中心点的时候，要注意中心点有两种情况。
    //            一个元素可以作为中心点，两个元素也可以作为中心点。
    int result = 0;
    for (int i = 0; i < s.length(); i++) {
        result += extend(s, i, i, s.length());  // 以1个字符作为中心点
        result += extend(s, i, i + 1, s.length());  // 以2个字符作为中心点
        // 三个字符等于一个字符左右添加元素，所以奇数都可以由一个中心点推出来
        // 四个字符等于二个字符左右添加元素，所以偶数都可以由二个中心点推出来
    }
    return result;
}
/**
         * 循环扩散的判断是否为回文字串（向2边扩散，而不是收缩）
         *
         * @param s
         * @param i
         * @param j
         * @param n
         * @return
         */
int extend(String s, int i, int j, int n) {
    int res = 0;    // 回文串的个数
    while (i >= 0 && j < s.length() && s.charAt(i) == s.charAt(j)) {    // 扩散查找，如果不满足相等直接退出循环
        i--;   // i向左
        j++;   // j向右
        res++;
    }
    return res;
}