Set哈希集合

哈希集是集合的实现之一，它是一种存储不重复值的数据结构。使用set可以快速进行查重。在大小不确定时，使用数组可能会无法计算，而且如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费,此时可以考虑使用HashSet，但是直接使用set 不仅占用空间比数组大，而且速度要比数组慢，set把数值映射到key上都要做hash计算的。

模板

/*
 * Template for using hash set to find duplicates.
 */
boolean findDuplicates(List<Type>& keys) {
    // Replace Type with actual type of your key
    Set<Type> hashset = new HashSet<>();
    for (Type key : keys) {
        if (hashset.contains(key)) {
            return true;
        }
        hashset.insert(key);
    }
    return false;
}

两个数的交集

题目描述：

力扣链接🔗

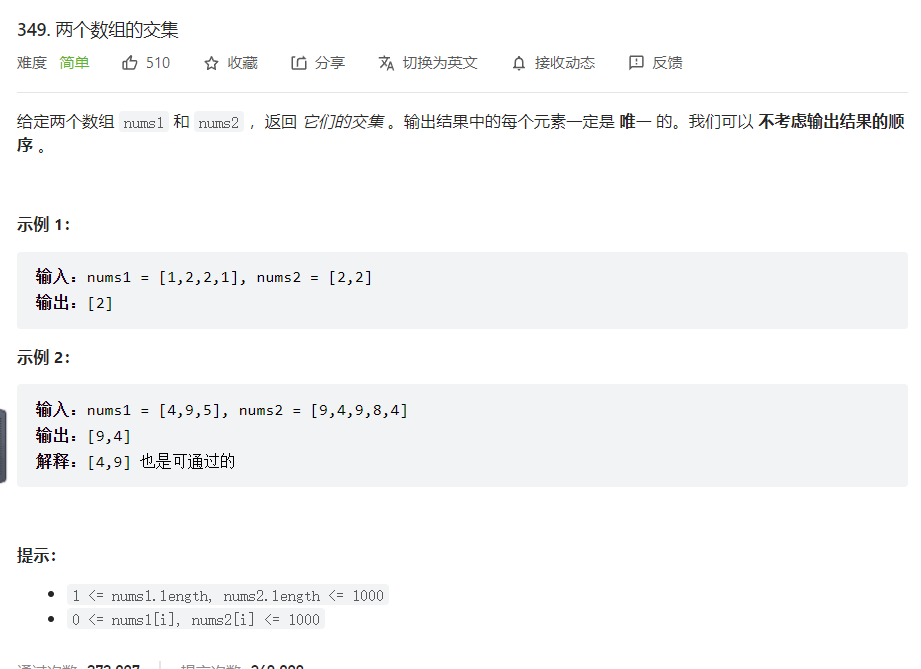
题目分析：

要注意，使用数组来做哈希的题目，是因为题目都限制了数值的大小。而这道题目没有限制数值的大小，就无法使用数组来做哈希表了。而且如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。

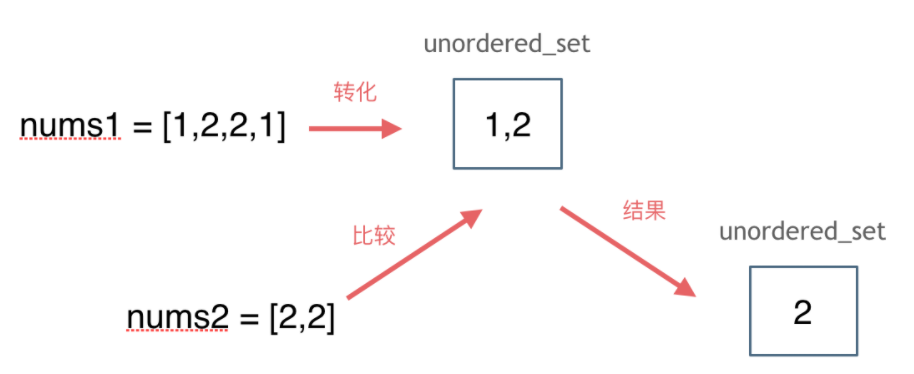
代码：

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        // 判断长度为空
        if (nums1.length == 0 || nums2.length == 0) {
            return new int[]{};
        }
        // 此题去重且不考虑顺序，可以使用hashset
        Set<Integer> set = new HashSet<>();
        Set<Integer> resSet = new HashSet<>();
        // 将nums2放入set
        for (int i = 0; i < nums2.length; i++) {
            set.add(nums2[i]);
        }
        for (int i = 0; i < nums1.length; i++) {
            // 将存在的元素放入resSet中
            if (set.contains(nums1[i])) {
                resSet.add(nums1[i]);
            }
        }
        int index = 0;
        int[] ints = new int[resSet.size()];
        // 转化为int数组
        for (Integer value : resSet) {
            ints[index++] = value;
        }
        return ints;
    }
}

快乐数

题目描述

力扣链接🔗

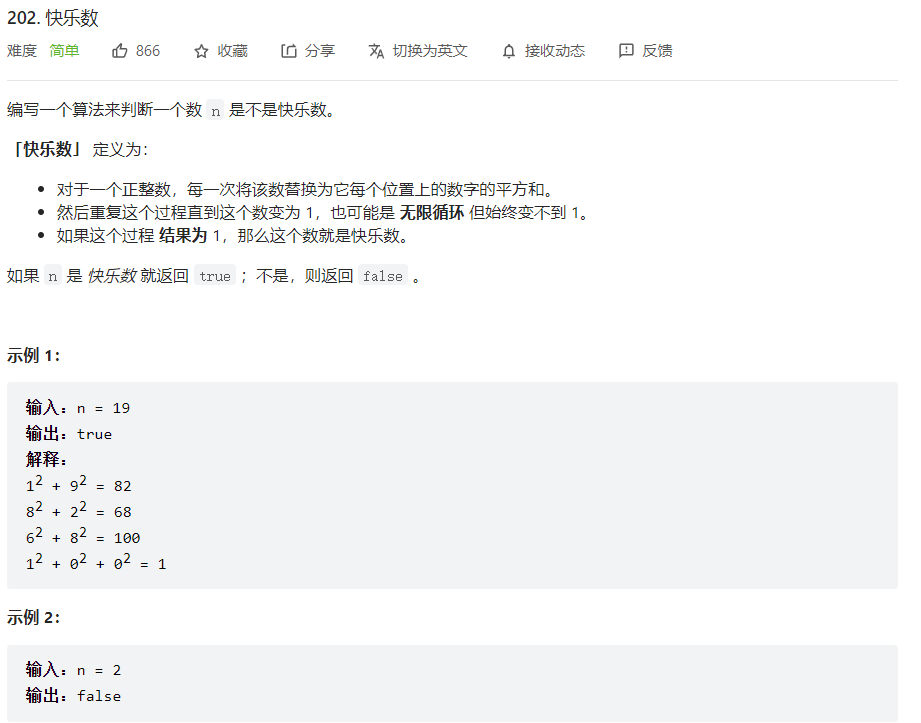
题目分析：

当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法了。题目中说了会 无限循环，那么也就是说求和的过程中，sum会重复出现，这对解题很重要！所以这道题目使用哈希法，来判断这个sum是否重复出现，如果重复了就是return false， 否则一直找到sum为1为止。

代码：

class Solution {
    /**
     * 使用hashset记录
     * @param n
     * @return
     */
    public boolean isHappy(int n) {
        Set<Integer> set = new HashSet<>();
        int sum = getNextNumber(n);
        while (sum != 1) {
            sum = getNextNumber(sum);
            // 如果分解后平方还是以前存在过的数，即是一直循环，不满足快乐数
            if (set.contains(sum)) {
                return false;
            }
            set.add(sum);
        }
        return true;
    }
    /**
     * 分解整数的方法
     * @param n
     * @return
     */
    private int getNextNumber(int n) {
        int temp, res = 0;
        while (n > 0) {
            temp = n % 10;
            n = n / 10;
            res += temp * temp;
        }
        return res;
    }
}

其他题目

只出现依次的数字

（力扣链接🔗）

存在重复元素

（力扣链接🔗）

环形链表Ⅱ

羽雀链接🔗