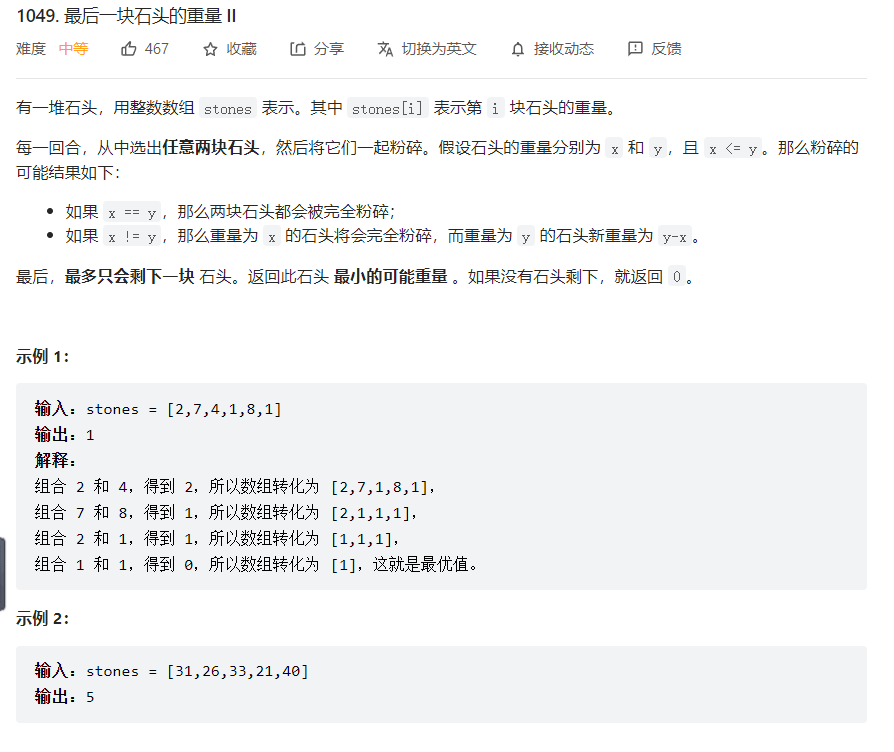
题目描述

image.png

解题思路

本题如何转化为0-1背包呢？
可以使用整体的思想，将所有石头分为2半，求整体相撞的差值，也就和分割等和子集有了一点关系了。
背包代表石头的总重量。
商品代表数组的一个石头。
重量代表数组的一个石头。

  • 确定dp数组以及下标的含义

dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背dp[j]这么重的石头。

  • 递推公式

dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
一些同学可能看到这dp[j - stones[i]] + stones[i]中 又有- stones[i] 又有+stones[i]，看着有点晕乎。
还是要牢记dp[j]的含义，要知道dp[j - stones[i]]为 容量为j - stones[i]的背包最大所背重量。

  • dp数组如何初始化

因为提示中给出1 <= stones.length <= 30，1 <= stones[i] <= 1000，所以最大重量就是30 * 1000 而我们要求的target其实只是最大重量的一半，所以dp数组开到15000大小就可以了。也可以计算出总重量除以2，题目告诉石头重量都是大于0，初始化全为0即可，保证后面递归公式不被覆盖。

  • 确定遍历顺序

注意滚动数组的遍历顺序。

  • 举例推导dp数组

举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下：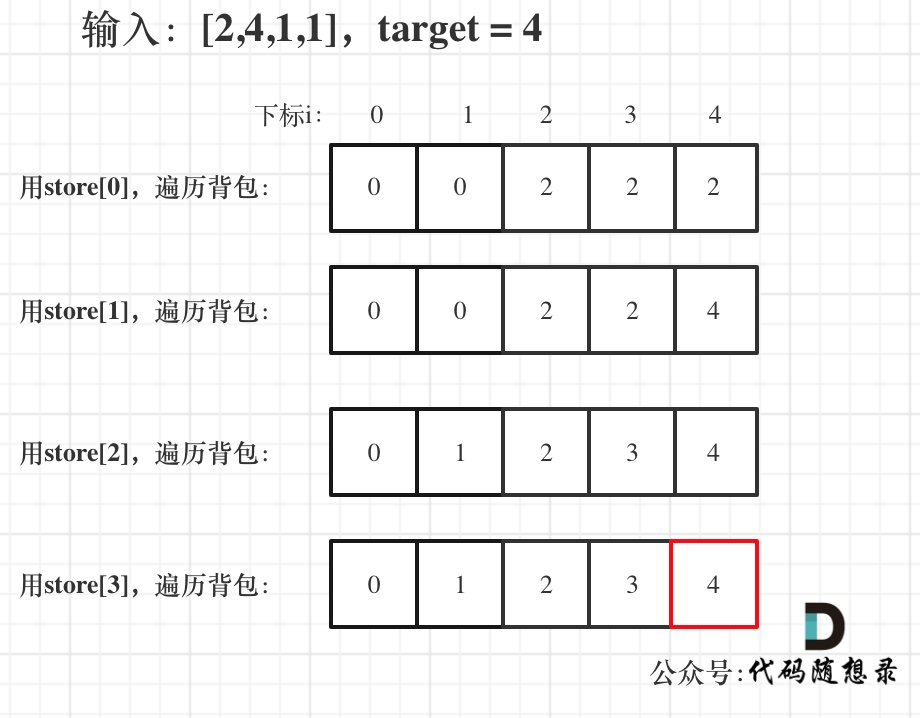
image.png
最后计算出一半的石头总重量为dp[target]，另一堆即是sum-dp[target]，相碰即为（sum-dp[target]）- dp[target]。

  1. /**
  2.          * 大体思路：
  3.          * 将石头所有重量总和分为2半，sum / 2 即为背包容量
  4.          * 在一半的背包容量之下，能装多少重量的石头，找到最大后，另一半也只能抵消背包装的最大重量(此时sum / 2 是向下取整)，如果完全抵消就是0，如果没有完全抵消就是最小的结果
  5.          * 时间复杂度：O(m × n) , m是石头总重量（准确的说是总重量的一半），n为石头块数
  6.          * 空间复杂度：O(m)
  7.          * @param stones
  8.          * @return
  9.          */
  10. public int lastStoneWeightII(int[] stones) {
  11.     int[] dp = new int[15001];  // 按照题意申请空间
  12.     int sum = 0;
  14.     for (int i = 0; i < stones.length; i++) {
  15.         sum += stones[i];
  16.     }
  18.     int bagSize = sum / 2;
  19.     for (int i = 0; i < stones.length; i++) {
  20.         for (int j = bagSize; j >= stones[i]; j--) {    // 倒序遍历
  21.             dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
  22.         }
  23.     }
  25.     // 在计算target的时候，target = sum / 2 因为是向下取整，所以sum - dp[target] 一定是大于等于dp[target]的。
  26.     return sum - dp[bagSize] - dp[bagSize]; // 得到最小的相减值
  27. }
  • 时间复杂度：O(m × n) , m是石头总重量（准确的说是总重量的一半），n为石头块数
  • 空间复杂度：O(m)